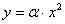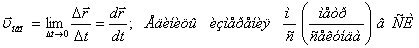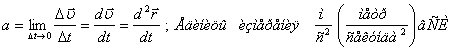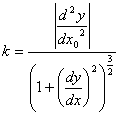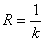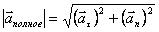частица движется равномерно по траектории изображенной на рисунке в каких точках ускорение равно 0

07.07.202219.07.2022 admin 0 Comments

Изучение равномерного движения материальной точки в плоскости по криволинейной траектории

Страницы работы

Содержание работы

I. Задание в соответствии с вариантом

Частица движется равномерно со скоростью 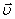по плоской траектории y(x). Найти ускорение частицы в точке x=0 и радиус кривизны траектории в этой точке, если траектория:

а) парабола

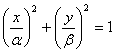
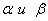
б) эллипс , где постоянные.

Построить график зависимости ускорения частицы и радиуса кривизны траектории от коэффициентов .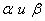

II. Краткое теоретическое содержание

1. Явление, изучаемое в РГР

В РГР изучается равномерное движение материальной точки в плоскости по криволинейной траектории.

2. Определение основных физических понятий, объектов, процессов и величин.

Материальная точка – это тело, обладающее массой, формой и размерами которого в данной задаче можно пренебречь.

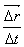
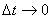
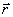
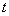
Скоростью материальной точки называется предел средней скорости при , т.е. производная от радиуса-вектора по времени :

Вектор скорости направлен по касательной к траектории точки в сторону ее движения.

Равномерное движение – это такое движение, при котором за любые равные промежутки времени тело проходит равные участки пути.

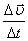
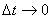
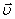
Ускорением материальной точки называется предел среднего ускорения при , т.е. производная от вектора скорости по времени:

Траектория движения материальной точки – это линия, которую описывает эта точка при своем движении.

Криволинейное движение тела – это такое движение тела, при котором его траектория движения отлична от прямой линии.

Любое криволинейное движение можно представить как движение по отрезкам и(или) дугам окружностей.

Кривизна плоской линии (не по определению). Если линия задана уравнением y=f(x), то ее кривизна вычисляется по формуле:

Радиус кривизны – величина, обратная кривизне:

3. Законы и соотношения, описывающие изучаемые процессы.

Модуль полного ускорения материальной точки может быть представлен как корень из суммы квадратов тангенциального и нормального ускорений:

Тангенциальное ускорение отвечает за изменение модуля скорости, а нормальное ускорение отвечает за изменение направления скорости.

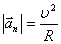
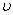
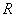
В случае равномерного движения по криволинейной траектории тангенциальное ускорение равно 0, нормальное же ускорение в каждой точке траектории можно вычислить таким образом , где — это скорость тела в точке, а — радиус кривизны траектории в этой точке.

4. Пояснения к физическим величинам, входящим в формулы, и единицы их измерения.

(кривизна траектории в некоторой точке M) – это предел отношения угла поворота касательной к длине дуги S (MN), при , т.е. . Единицей измерения кривизны кривой в точке служит .

Источник

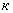
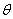
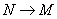
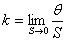
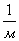
Частица движется равномерно по траектории изображенной на рисунке в каких точках ускорение равно 0

Камень бросили под углом к горизонту. Сопротивление воздуха пренебрежимо мало. В верхней точке траектории кинетическая энергия камня равна его потенциальной энергии (относительно поверхности Земли). Под каким углом к горизонту бросили камень? Ответ приведите в градусах.

Пусть скорость в начале броска равна а скорость в верхней точке траектории равна В верхней точке траектории вертикальная составляющая скорости равна нулю, поэтому По условию, в верхней точке траектории потенциальная энергия камня равна кинетической, используя этот факт, найдём

Воспользуемся законом сохранения энергии, энергия камня в начале броска равна энергии камня в верхней точке его траектории:

Косинус угла броска камня будет равен отношению к

Следовательно, угол броска равен 45°.

Камень бросили под углом к горизонту. Сопротивление воздуха пренебрежимо мало. В верхней точке траектории кинетическая энергия камня в 3 раза больше его потенциальной энергии (относительно поверхности Земли). Под каким углом к горизонту бросили камень? Ответ приведите в градусах.

Пусть скорость в начале броска равна а скорость в верхней точке траектории равна В верхней точке траектории вертикальная составляющая скорости равна нулю, поэтому По условию, в верхней точке траектории кинетическая энергия камня в три раза больше потенциальной, используя этот факт, найдём

Косинус угла броска камня будет равен отношению к

Следовательно, угол броска равен 30°.

Аналоги к заданию № 6129: 6164 Все

Тело бросили с горизонтальной площадки под углом 30° к горизонту с начальной скоростью 20 м/с. Затем бросок повторили, сообщив телу ту же по модулю начальную скорость, но увеличив угол её наклона к горизонту. Пренебрегая сопротивлением воздуха, определите, как при втором броске по сравнению с первым изменятся следующие физические величины: отношение максимальной высоты подъёма тела к дальности его полёта; кинетическая энергия тела в высшей точке траектории.

Для каждой величины определите соответствующий характер изменения:

Запишите в ответ цифры, расположив их в порядке, соответствующем таблице:

Отношение максимальной высоты подъёма тела к дальности его полёта

Кинетическая энергия тела в высшей точке траектории

Дальность полета и максимальная высота определяются формулами:

Их отношение равно:

Таким образом, увеличение угла броска приведет к увеличению отношения максимальной высоты подъёма тела к дальности его полёта

Чем больше угол броска, тем большей высоты достигнет тело. Отсюда следует, что во втором случае потенциальная энергия тела в высшей точке траектории будет больше чем в первом случае.В начале своего движения тело обладало только кинетической энергией, а в высшей точке траектории оно будет обладать как кинетической так и потенциальной энергией. Исходя из того, что начальная скорость тела в первом и втором случае одинакова, согласно закону сохранения энергии, увеличение потенциальной энергии в высшей точке траектории приведет к уменьшению кинетической энергии в высшей точке.

Аналоги к заданию № 9498: 9530 Все

Человек ростом h = 1,6 м, стоя на земле, кидает мяч из-за головы и хочет перебросить его через забор высотой H = 4,8 м, находящийся на расстоянии l = 6,4 м от него. Определите модуль скорости, с которой необходимо бросить мяч, чтобы он перелетел через забор, коснувшись его в верхней точке своей траектории? Сопротивлением воздуха пренебречь.

Известно, что в верхней точке траектории тела, брошенного под углом к горизонту, скорость направлена горизонтально. Без действия сопротивления воздуха тело движется с ускорением свободного падения. Поэтому по оси Ox движение является равномерным (горизонтальная проекция скорости одинакова на всем пути), по оси Oy движение равноускоренное, при этом в верхней точки траектории вертикальная проекция скорости равна 0.

Применим закон сохранения энергии для движения мячика от точки броска до верхней точки траектории

Учитывая, что найдем вертикальную проекцию начальной скорости:

Скорость тела при равноускоренном движении по вертикали равна откуда время подъема до верхней точки траектории

Зная расстояние, которое мяч пролетел по горизонтали, найдем горизонтальную составляющую начальной скорости

Тогда начальная скорость броска мяча

Человек ростом h, стоя на Земле, бросает из-за головы камень и хочет перебросить его через забор высотой H, находящийся на расстоянии L от человека. Найдите угол, под которым нужно бросить камень, чтобы он перелетел через забор, коснувшись его в верхней точке своей траектории.

Применим закон сохранения энергии для движения мячика от точки броска до верхней точки траектории

Учитывая, что найдем вертикальную проекцию начальной скорости:

Выразив из представленных формул горизонтальную и вертикальную составляющие начальной скорости, найдем тангенс угла броска:

откуда

Ответ:

Какие законы Вы использовали для описания движения мяча? Обоснуйте их применение к данному случаю.

При отсутствии действия внешних сил (сила сопротивления воздуха равна нулю) система «мяч — Земля» является замкнутой. Поэтому в инерциальной системе отсчета применим закон сохранения энергии.

Перейдем к решению. Известно, что в верхней точке траектории тела, брошенного под углом к горизонту, скорость направлена горизонтально. Без действия сопротивления воздуха тело движется с ускорением свободного падения. Поэтому по оси Ox движение является равномерным (горизонтальная проекция скорости одинакова на всем пути), по оси Oy движение равноускоренное, при этом в верхней точки траектории вертикальная проекция скорости равна 0.

Применим закон сохранения энергии для движения мячика от точки броска до верхней точки траектории

Учитывая, что найдем вертикальную проекцию начальной скорости:

Тогда начальная скорость броска мяча

Частица массой m, несущая заряд q, движется в однородном магнитном поле с индукцией В по окружности радиусом R со скоростью Как изменятся радиус траектории, период обращения и кинетическая энергия частицы при увеличении скорости её движения?

Для каждой величины определите соответствующий характер изменения:

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

обращенияКинетическая

На заряженную частицу со стороны магнитного поля действует сила Лоренца, которая сообщает ей центростремительное ускорение. Второй закон Ньютона приобретает вид: Отсюда следует, что при увеличении скорости движения частицы радиус траектории увеличивается. Период обращения связан со скоростью движения и радиусом траектории соотношением В силу того, что при увеличении скорости период обращения не изменяется. Кинетическая энергия равна Следовательно, при увеличении скорости кинетическая энергия также увеличивается.

Эта строчка следствие второго закона Ньютона:

. А поскольку в данной задаче величина поля не изменяется, частица одна и та же, меняется только ее скорость, заключаем, что при увеличении скорости не изменяется, а значит, не изменяется и , что, в свою очередь, ведет к неизменности периода.

Частица массой m, несущая заряд q, движется в однородном магнитном поле с индукцией В по окружности радиусом R со скоростью Как изменится радиус траектории, период обращения и кинетическая энергия частицы при уменьшении скорости ее движения?

Для каждой величины определите соответствующий характер изменения:

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

обращенияКинетическая

На заряженную частицу со стороны магнитного поля действует сила Лоренца, которая сообщает ей центростремительное ускорение. Второй закон Ньютона приобретает вид: Отсюда следует, что при уменьшении скорости движения частицы радиус траектории уменьшается. Период обращения связан со скоростью движения и радиусом траектории соотношением В силу того, что при уменьшении скорости период обращения не изменяется. Кинетическая энергия равна Следовательно, при уменьшении скорости кинетическая энергия также уменьшается.

Положительный заряд перемещается в однородном электростатическом поле из точки 1 в точку 2 по разным траекториям. При перемещении по какой траектории электрическое поле совершает наименьшую работу?

4) работа одинакова при движении по всем траекториям

Электростатическое поле потенциально. Это значит, что работа электрического поля не зависит от формы траектории и определяется только начальным и конечным положениями заряда.

Точечное тело бросают с поверхности земли под углом α к горизонту с начальной скоростью V₀. Как изменятся при увеличении угла бросания тела

А) отношение максимальной высоты подъёма к дальности полёта и

Б) отношение модуля импульса в верхней точке траектории к модулю импульса при броске?

Для каждой величины определите соответствующий характер изменения:

Запишите в ответ цифры, расположив их в порядке, соответствующем таблице:

Отношение максимальной высоты подъёма к дальности полёта

Отношение модуля импульса в верхней точке траектории к модулю импульса при броске

Максимальная высота подъёма равна дальность полёта равна Их отношение увеличится при увеличении угла бросания тела.

В наивысшей точке траектории вертикальная составляющая скорости тела равна нулю, следовательно, модуль скорости тела равен модулю проекции скорости тела на горизонтальную ось: При увеличении угла броска косинус уменьшится, следовательно, уменьшится и Поскольку модуль начальной скорости остался прежним, отношение модуля импульса в верхней точке траектории к модулю импульса при броске уменьшится.

Сравниваются импульсы тел в верхней точке траектории, в которой проекция на ось у равна 0. Ошибки нет.

Ученик исследовал движение шарика, сброшенного горизонтально со стола. Для этого он измерил координаты летящего шарика в разные моменты времени его движения и заполнил таблицу:

t, c	0,05	0,1	0,15	0,2
x, см	5,5	13,5	17,5	24
y, см	1,5	4,5	11,5	20

Погрешность измерения координат равна 1 см, а промежутков времени — 0,01 с. На каком из графиков верно представлена наиболее вероятная траектория движения шарика?

В задании нужно найти график, на котором наиболее верно представлена траектория движения шарика, поэтому графики 3 и 4 сразу отпадают, так как на них отображена не возможная траектория, а зависимость координат от времени. Остается выбрать между графиками 1 и 2. Как известно, свободно падающее тело летит по параболе. Следовательно, через экспериментальные точки нужно проводить параболическую интерполяционную кривую, что и сделано на рисунке 1.

В задании нужно найти график, на котором наиболее верно представлена траектория движения шарика, поэтому графики 3 и 4 сразу отпадают, так как на них отображена не возможная траектория, а зависимость координат от времени. Остается выбрать между графиками 1 и 2. Известно, что свободно падающее тело летит по параболе. Следовательно, через экспериментальные точки нужно проводить параболическую интерполяционную кривую, что и сделано на рисунке 2.

В установке, изображённой на рисунке, грузик А соединён перекинутой через блок нитью с бруском В, лежащим на горизонтальной поверхности трибометра, закреплённого на столе. Грузик отводят в сторону, приподнимая его на некоторую высоту h, и отпускают. Какую величину должна превзойти эта высота, чтобы брусок сдвинулся с места в тот момент, когда грузик проходит нижнюю точку траектории? Масса грузика m, масса бруска М, длина свисающей части нити L, коэффициент трения между бруском и поверхностью Трением в блоке, а также размерами блока пренебречь.

1. На брусок B, пока он не пришёл в движение, действует сила тяжести сила реакции опоры сила натяжения нити и сила трения покоя максимальное значение которой Для того, чтобы он пришёл в движение, должно выполняться условие

На грузик А в нижней точке траектории действует сила тяжести сила натяжения нити модуль которой равен модулю силы и равен При этом грузик в этой точке движется со скоростью и на него действует центростремительное ускорение направленное по радиусу к центру окружности и равное

2. Запишем второй закон Ньютона для каждого тела в проекциях:

3. По закону сохранения энергии потенциальная энергия грузика, поднятого на высоту равна кинетической энергии грузика в нижней точке траектории:

4. С учётом условия движения бруска получаем

Ответ:

В установке, изображённой на рисунке, грузик А соединён перекинутой через блок нитью с бруском В, лежащим на горизонтальной поверхности трибометра, закреплённого на столе. Грузик отводят в сторону, приподнимая его на высоту h, и отпускают. Длина свисающей части нити равна L. Какую величину должна превзойти масса грузика, чтобы брусок сдвинулся с места в момент прохождения грузиком нижней точки траектории? Масса бруска М, коэффициент трения между бруском и поверхностью Трением в блоке, а также размерами блока пренебречь.

1. На брусок B, пока он не пришёл в движение, действуют сила тяжести сила реакции опоры сила натяжения нити и сила трения покоя максимальное значение которой Для того чтобы он пришёл в движение, должно выполняться условие

На грузик А в нижней точке траектории действуют сила тяжести и сила натяжения нити модуль которой равен модулю силы и равен При этом грузик в этой точке движется со скоростью то есть он движется с центростремительным ускорением направленным по радиусу к центру окружности и равным