через какое время скорость тела которому сообщили вверх по наклонной плоскости скорость v
Методические рекомендации для самостоятельной работы студентов при решении задач по физике (стр. 7 )
 | Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 |
x2=v2cosa×t ; y2=v2sina×t – gt2/2
В момент попадания камня в утку: x1=x2 и y1=y2.

Из уравнения (1) выразим время t:

Решив это уравнение относительно h, получим:
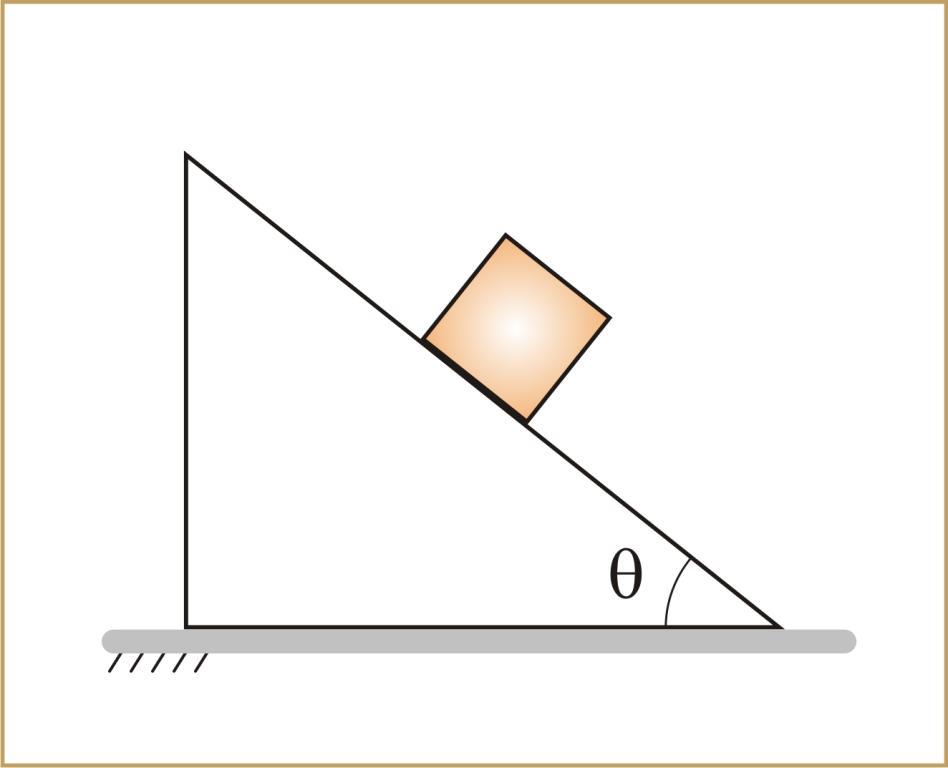
Через какое время скорость тела, которому была сообщена скорость Vo, направленная вверх по наклонной плоскости, снова будет равна Vo. Коэффициент трения k, угол наклона a. Тело начинает двигаться со скоростью Vо, находясь посередине наклонной плоскости.
Дано; Vo, a, k; Найти: t.
РЕШЕНИЕ: Вначале тело будет двигаться вверх по наклонной плоскости с отрицательным ускорением а1 до остановки, а затем будет двигаться ускоренно вниз (с ускорением а2). Скорость тела будет равна vo в момент времени t2 при движении вниз.
Искомое время t=t1+t2 (1), где t1 время подъема тела до остановки; t2 – время спуска до достижения скорости vo. Очевидно, что t1= vo/a1 (2), а t2= vo/a2 (3).
Т. о. задача сводится к нахождению a1 и a2.
Рис. 2



При движении вверх в проекциях на оси:
Из этих уравнений получаем: N=mg×cosa, Fтр=k×N,
Подставив значения a1 и а2 в (2) и (3), а значения t1 и t2 в (1), получим:

Следует отметить, что решение имеет смысл только при угле a, для которого tga>k. При меньшем угле наклона груз не будет соскальзывать.
Пуля попадает в ящик с песком и застревает в нем (рис.3). На сколько сожмется пружина жесткостью k, удерживающая ящик, если пуля имеет массу m, скорость v, а масса ящика М? (трение не учитывать).

После попадания пули в ящик с
песком, ящик (вместе с застрявшей
в нем пулей) приобретает скорость vo Рис.3
и следовательно запас кинетической
энергии Ek=(M+m) vo 2/2.
Эта энергия переходит в энергию упругой деформации пружины En=kx2/2. На основании закона сохранения энергии можно записать Ek=En, или
(M+m)×vo2/2=kx2/2, откуда
Начальную скорость ящика найдем из закона сохранения импульса. В данном случае (взаимодействие абсолютно неупругое) он запишется так:
mv=(M+m)vo, откуда vo=mv/(M+m). Подставив значение vo в формулу для X, получим:
Следует подчеркнуть, что при неупругом взаимодействии механическая энергия до удара больше, чем механическая энергия после удара, т. е. mv2/2 >kx2/2, т. к. часть механической энергии переходит во внутреннюю (в тепло).
Внутри сферы радиуса R, вращающейся с угловой скоростью w, покоится небольшое тело массы m. Радиус-вектор, соединяющий его с центром сферы составляет угол j с вертикалью (см. рис.4). Найти силу трения между телом и сферой.



Решаем его относительно Fтр и получаем:
Два точечных заряда q1=+q и q2=-q (q=10-8 Кл) расположены на расстоянии d=3 см друг от друга. Определить напряженность и потенциал электрического поля в точке А, расположенной на расстоянии L=4см от заряда q1 на перпендикуляре к линии, соединяющей заряды (см. рис.5)
ДАНО: q=10-8 Кл, d=0,03м, L=0,04м.
РЕШЕНИЕ: Напряженность электрического поля величина векторная и подчиняется принципу

Е1=q/4peoL2 и E2=q/4peo(L2+d2)
напряженность поля, создаваемого в точке А зарядами q1 и q2 (см. рис.5). Модуль вектора Е найдем по теореме косинусов:

где 
Через какое время скорость тела, которому сообщили вверх по наклонной скорость 10 м/с, снова будет равна 10 м/с?
| 🎓 Заказ №: 21972 |
| ⟾ Тип работы: Задача |
| 📕 Предмет: Физика |
| ✅ Статус: Выполнен (Проверен преподавателем) |
| 🔥 Цена: 149 руб. |
👉 Как получить работу? Ответ: Напишите мне в whatsapp и я вышлю вам форму оплаты, после оплаты вышлю решение.
➕ Как снизить цену? Ответ: Соберите как можно больше задач, чем больше тем дешевле, например от 10 задач цена снижается до 50 руб.
➕ Вы можете помочь с разными работами? Ответ: Да! Если вы не нашли готовую работу, я смогу вам помочь в срок 1-3 дня, присылайте работы в whatsapp и я их изучу и помогу вам.
⚡ Условие + 37% решения:
Через какое время скорость тела, которому сообщили вверх по наклонной скорость 10 м/с, снова будет равна 10 м/с? Коэффициент трения 0.2, угол между плоскостью и горизонтом 30.

Готовые задачи по физике которые сегодня купили:
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Движение по наклонной плоскости тела: скорость, трение, время
Основная формула динамики

Конечно же, речь идет о втором законе, который постулировал Исаак Ньютон в XVII веке, изучая механическое движение твердых тел. Запишем его в математической форме:
Действие внешней силы F¯ вызывает появление линейного ускорения a¯ у тела с массой m. Обе векторные величины (F¯ и a¯) направлены в одну и ту же сторону. Сила в формуле является результатом действия на тело всех сил, которые присутствуют в системе.
В случае движения вращения второй закон Ньютона записывается в виде:
Формулы кинематики
Решение задач на движение по наклонной плоскости требует знания не только главной формулы динамики, но и соответствующих выражений кинематики. Они связывают в равенства ускорение, скорость и пройденный путь. Для равноускоренного (равнозамедленного) прямолинейного движения применяются следующие формулы:
Если движение осуществляется по круговой траектории (вращение вокруг оси), тогда следует использовать такие формулы:
Линейные и угловые характеристики друг с другом связаны формулами:
Движение по наклонной плоскости: силы
Под этим движением понимают перемещение некоторого объекта вдоль плоской поверхности, которая наклонена под определенным углом к горизонту. Примерами может служить соскальзывание бруска по доске или качение цилиндра по металлическому наклоненному листу.
Для определения характеристик рассматриваемого типа движения необходимо в первую очередь найти все силы, которые действуют на тело (брусок, цилиндр). Они могут быть разными. В общем случае это могут быть следующие силы:
Первые три из них присутствуют всегда. Существование последних двух зависит от конкретной системы физических тел.
Чтобы решать задачи на перемещение по плоскости наклонной необходимо знать не только модули сил, но и их направления действия. В случае, если тело по плоскости скатывается, сила трения неизвестна. Однако она определяется из соответствующей системы уравнений движения.
Методика решения
Решения задач данного типа начинается с определения сил и их направлений действия. Для этого в первую очередь рассматривают силу тяжести. Ее следует разложить на два составляющих вектора. Один из них должен быть направлен вдоль поверхности наклонной плоскости, а второй должен быть ей перпендикулярен. Первая составляющая силы тяжести, в случае движения тела вниз, обеспечивает его линейное ускорение. Это происходит в любом случае. Вторая равна силе реакции опоры. Все эти показатели могут иметь различные параметры.
Сила трения при движении по наклонной плоскости всегда направлена против перемещения тела. Если речь идет о скольжении, то вычисления довольно просты. Для этого следует использовать формулу:
Если в системе присутствуют только указанные три силы, тогда их результирующая вдоль наклонной плоскости будет равна:
Зная силу F, можно по закону Ньютона определить линейное ускорение a. Последнее, в свою очередь, используется для определения скорости движения по наклонной плоскости через известный промежуток времени и пройденного телом расстояния. Если вникнуть, то можно понять, что все не так уж и сложно.
В случае, когда тело скатывается по наклонной плоскости без проскальзывания, суммарная сила F будет равна:
Учитывая, что мы имеем два уравнения и две неизвестных (α и a связаны друг с другом), можно легко решить эту систему, а значит, и задачу.
Теперь рассмотрим, как использовать описанную методику при решении конкретных задач.
Задача на движение бруска по наклонной плоскости
Деревянный брусок находится в верхней части наклонной плоскости. Известно, что она имеет длину 1 метр и располагается под углом 45o. Необходимо вычислить, за какое время брусок опустится по этой плоскости в результате скольжения. Коэффициент трения принять равным 0,4.
Записываем закон Ньютона для данной физической системы и вычисляем значение линейного ускорения:
Поскольку нам известно расстояние, которое должен пройти брусок, то можно записать следующую формулу для пути при равноускоренном движении без начальной скорости:
Откуда следует выразить время, и подставить известные значения:
t = √(2*S/a) = √(2*1/4,162) ≈ 0,7 с
Таким образом, время движения по наклонной плоскости бруска составит меньше секунды. Заметим, что полученный результат от массы тела не зависит.
Задача со скатывающимся по плоскости цилиндром
Цилиндр радиусом 20 см и массой 1 кг помещен на наклонную под углом 30o плоскость. Следует вычислить его максимальную линейную скорость, которую он наберет при скатывании с плоскости, если ее длина составляет 1,5 метра.
Запишем соответствующие уравнения:
Момент инерции I цилиндра вычисляется по формуле:
Подставим это значение во вторую формулу, выразим из нее силу трения Fr и заменим полученным выражением ее в первом уравнении, имеем:
Мы получили, что линейное ускорение не зависит от радиуса и массы скатывающегося с плоскости тела.
Зная, что длина плоскости составляет 1,5 метра, найдем время движения тела:
Тогда максимальная скорость движения по наклонной плоскости цилиндра будет равна:
v = a*t = a*√(2*S/a) = √(2*S*a) = √(4/3*S*g*sin(φ))
Подставляем все известные из условия задачи величины в конечную формулу, получаем ответ: v ≈ 3,132 м/c.
Через какое время скорость тела которому сообщили вверх по наклонной плоскости скорость v
Тело брошено вертикально вверх. Через 0,5 с после броска его скорость 20 м/с. Какова начальная скорость тела? Сопротивлением воздуха пренебречь. (Ответ дайте в метрах в секунду.)
Поскольку сопротивлением воздуха можно пренебречь, на брошенное тело действует только сила тяжести, которая сообщает ему постоянное ускорение свободного падения, направленное вниз. Следовательно, скорость меняется со временем по закону Отсюда находим начальную скорость тела
Условия похожи, но вопросы разные. Тут известна скорость в момент времени 0,5 с, и просят найти начальную скорость. А в задаче 135 известна начальная скорость, и просят найти скорость через 0,5 с. «Шаги» по времени делаются в разные стороны.
У нас есть векторное соотношение, описывающее закон изменения вектора скорости вблизи поверхности Земли:
.
Спроектируем его на вертикальную ось, направленную вверх: начальная скорость направленна вверх, поэтому ее проекция положительна; ускорение свободного падения направлено вниз, поэтому его проекция отрицательна. В итоге имеем:
.
В этой формуле уже учтено направление всех векторов, здесь считается, что . Никаких дополнительных знаков не возникает. Вначале
положительна, это соответствует полету тела вверх, в какой-то момент
становится отрицательной, это означает, что тело начало возвращаться обратно.
А что было бы если воздухом нельзя пренебречь?
Тогда движение не было бы равноускоренным. На тело бы действовала сила сопротивления воздуха. Чтобы описать движение, пришлось бы решать дифференциальное уравнение — второй закон Ньютона для тела. При этом необходимо было бы как-то смоделировать действие силы сопротивления. Обычно в таких случаях считают, что эта сила равна где
— вектор скорости тела, а
— постоянный коэффициент.
как нашли ускорение?
Земля сообщает всем свободно падающим телам одинаковое ускорение, ускорение свободного падения, его значение приведено в разделе Справочник
Будьте внимательнее. В решении используется правильная формула, просто в последней строчке из нее выражена начальная скорость.
чем эта задача отличается от A1 № 135?? почему тут пишется изначально формула с минусом, а решается с плюсом? а в 135, похожей задаче и пишется и решается по одной формуле с минусом?!
Будьте внимательнее, в этой задаче рассчитывается начальная скорость . Она сначала выражается из общего выражения:
. А потом подставляются конкретные значения.
Через какое время скорость тела которому сообщили вверх по наклонной плоскости скорость v
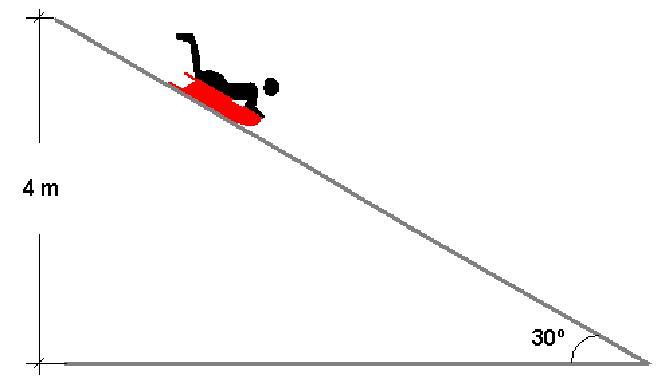
Тело съезжает вниз по гладкой наклонной плоскости с начальной высоты Н до уровня пола. Затем проводят опыт с другой наклонной плоскостью с меньшим углом наклона к горизонту; при этом начальную высоту H, с которой съезжает тело, оставляют прежней. Как в результате этого изменятся следующие физические величины: время соскальзывания тела до уровня пола, модуль скорости тела вблизи пола, модуль силы нормальной реакции наклонной плоскости?
Для каждой величины определите соответствующий характер изменения:
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ | ИХ ИЗМЕНЕНИЕ |
| А) Время соскальзывания тела до уровня пола | 1) увеличится |
| Б) Модуль скорости тела вблизи пола | 2) уменьшится |
| В) Модуль силы нормальной реакции наклонной плоскости | 3) не изменится |
Направим оси вдоль движения и перпендикулярно к нему. Запишем второй закон Ньютона в проекциях:
Отсюда видно, что при уменьшении угла наклона плоскости сила реакции опоры N увеличивается. (В — 1).
При соскальзывании потенциальная энергия тела вблизи пола полностью переходит в кинетическую
Поскольку высота горки не изменилась, скорость вблизи пола также не изменилась. (Б — 3).
Пройденный телом путь выражается через высоту наклонной плоскости и угол её наклона: С другой стороны, этот же путь при равноускоренном движении, рассчитывается по формуле
Приравнивая оба выражения, находим время:
откуда следует, что при уменьшении угла наклона время соскальзывании увеличится. (А — 1).