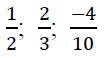числа бывают натуральные а еще какие
Числа: натуральные, целые, рациональные, иррациональные, действительные
Натуральные числа
Натуральные числа определение – это целые положительные числа. Натуральные числа используют для счета предметов и многих иных целей. Вот эти числа:
Это натуральный ряд чисел.
Ноль натуральное число? Нет, ноль не является натуральным числом.
Сколько натуральных чисел существует? Существует бесконечное множество натуральных чисел.
Каково наименьшее натуральное число? Единица — это наименьшее натуральное число.
Каково наибольшее натуральное число? Его невозможно указать, ведь существует бесконечное множество натуральных чисел.
Сумма натуральных чисел есть натуральное число. Итак, сложение натуральных чисел a и b:
с — это всегда натуральное число.
Произведение натуральных чисел есть натуральное число. Итак, произведение натуральных чисел a и b:
с — это всегда натуральное число.
Разность натуральных чисел Не всегда есть натуральное число. Если уменьшаемое больше вычитаемого, то разность натуральных чисел есть натуральное число, иначе — нет.
Частное натуральных чисел Не всегда есть натуральное число. Если для натуральных чисел a и b
где с — натуральное число, то это значит, что a делится на b нацело. В этом примере a — делимое, b — делитель, c — частное.
Делитель натурального числа — это натуральное число, на которое первое число делится нацело.
Каждое натуральное число делится на единицу и на себя.
Простые натуральные числа делятся только на единицу и на себя. Здесь имеется ввиду делятся нацело. Пример, числа 2; 3; 5; 7 делятся только на единицу и на себя. Это простые натуральные числа.
Единицу не считают простым числом.
Числа, которые больше единицы и которые не являются простыми, называют составными. Примеры составных чисел:
Единицу не считают составным числом.
Множество натуральных чисел составляют единица, простые числа и составные числа.
Множество натуральных чисел обозначается латинской буквой N.
Свойства сложения и умножения натуральных чисел:
переместительное свойство сложения
сочетательное свойство сложения
переместительное свойство умножения
сочетательное свойство умножения
распределительное свойство умножения
Целые числа
Целые числа — это натуральные числа, ноль и числа, противоположные натуральным.
Числа, противоположные натуральным — это целые отрицательные числа, например:
Множество целых чисел обозначается латинской буквой Z.
Рациональные числа
Рациональные числа — это целые числа и дроби.
Любое рациональное число может быть представлено в виде периодической дроби. Примеры:
Из примеров видно, что любое целое число есть периодическая дробь с периодом ноль.
Любое рациональное число может быть представлено в виде дроби m/n, где m целое число,n натуральное число. Представим в виде такой дроби число 3,(6) из предыдущего примера:
Другой пример: рациональное число 9 может быть представлено в виде простой дроби как 18/2 или как 36/4.
Множество рациональных чисел обозначается латинской буквой Q.
Подробнее о рациональных числах в разделе Рациональные числа.
Иррациональные числа
Иррациональные числа — это бесконечные непериодические десятичные дроби. Примеры:
Подробнее об иррациональных числах в разделе Иррациональные числа.
Действительные числа
Действительные числа – это все рациональные и все иррациональные числа.
Множество действительных чисел обозначается латинской буквой R.
Виды чисел.
У нас есть числа натуральные, целые, рациональные и иррациональные, а также вещественные или действительные и еще есть другие, но в школьной программе в основном используют эти числа.
Натуральные числа ( N ) − это числа, используемые для счета предметов. Нуль не является натуральным числом.
Например: 1; 2; 3; 132; 168; 326; 548; 10050…
Целые числа ( Z ) — множество чисел, получающееся в результате арифметических операций сложения (+) и вычитания (−) натуральных чисел.
Например: …−3; −2; 1; 0; 548; 10050…
Рациональные числа ( Q ) – это положительные и отрицательные числа можно представить в виде обыкновенной несократимой дроби вида: 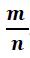
где m−целое число (числитель), n – натуральное число (знаменатель).
Например:
Иррациональные числа ( I ) − числа, которые не представимыми в виде дроби вида 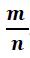
Например: √2; √5; π; e
Вещественные (действительные) числа ( R ).
Рациональные числа и иррациональные числа образуют множество действительных чисел.
Изобразим это множество чисел в виде рисунка:
Видно их вложенность друг в друга.
Подписывайтесь на канал на YOUTUBE и смотрите видео, подготавливайтесь к экзаменам по математике и геометрии с нами.
Что такое число
В данной публикации мы рассмотрим определение числа, перечислим его основные виды и отличия от цифры, разберем принцип образования чисел и их произношение. Представленная информация сопровождается примерами для лучшего понимания.
Определение числа
Число – это количественная характеристика чего-либо. Используется для подсчета количества, маркировки, измерения величин и т.д. Раньше для обозначений чисел использовались черточки, однако для записи больших значений такой способ был крайне неудобен. Представьте, сколько времени бы заняло рисование черточек для записи, к примеру, числа 745.
С развитием науки и математики в частности, была придумана десятичная система счисления, содержащая цифры 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9, которые называются арабскими. К слову, данная система применяется по сей и является самой распространенной.
Отличия чисел от цифр
Принцип образования чисел
С помощью десяти цифр можно записать любое натуральное число. В зависимости от того, сколько цифр содержится в числе, оно может быть:
Примеры:
1. Число “пятьдесят восемь” пишется так – “58”. То есть мы расставляем цифры по соответствующим разрядам:
2. Чтобы записать число “шестьсот двадцать шесть” нам нужны только две цифры – “6” и “2”, несмотря на то, что оно трехзначное:
Использование запятой
Для записи чисел могут использоваться не только цифры, но и запятые (в некоторых странах – точки). Делается это для отделения целой и дробной частей. Например:
Определение, запись, произношение и свойства десятичной дроби мы подробно рассмотрели в отдельной публикации.
Математика
Тестирование онлайн
Натуральные числа
Это числа, которые используются при счете: 1, 2, 3. и т.д.
Ноль не является натуральным.
Натуральные числа принято обозначать символом N.
Целые числа. Положительные и отрицательные числа
Натуральные числа, противоположные им и ноль называют целыми числами. Множество целых чисел обозначают символом Z.
Рациональные числа
Множество рациональных чисел обозначается Q. Все целые числа являются рациональными.
Иррациональные числа
Бесконечная непериодическая дробь называется иррациональным числом. Например:
Множество иррациональных чисел обозначается J.
Действительные числа
Множество всех рациональных и всех иррациональных чисел называется множеством действительных (вещественных) чисел.
Действительные числа обозначаются символом R.
Округление чисел
Округлить 8,759123. с точностью до целой части.
Округлить 8,759123. с точностью до десятой части.
Округлить 8,759123. с точностью до сотой части.
Округлить 8,759123. с точностью до тысячной части.
Основные числовые множества
Число — абстракция, используемая для количественной характеристики объектов. Числа возникли еще в первобытном обществе в связи с потребностью людей считать предметы. С течением времени по мере развития науки число превратилось в важнейшее математическое понятие.
Для решения задач и доказательства различных теорем необходимо понимать, какие бывают виды чисел. Основные виды чисел включают в себя: натуральные числа, целые числа, рациональные числа, действительные числа.
Основные числовые множества
Натуральные числа – это числа, получаемые при естественном счёте предметов, а вернее при их нумерации («первый», «второй», «третий». ). Множество натуральных чисел обозначается латинской буквой N (можно запомнить, опираясь на английское слово natural). Можно сказать, что N =
Действительные (вещественные) числа – это числа, которое применяются для измерения непрерывных величин. Множество действительных чисел обозначается латинской буквой R. Действительные числа включают в себя рациональные числа и иррациональные числа. Иррациональные числа – это числа, которые получаются в результате выполнения различных операций с рациональными числами (например, извлечение корня, вычисление логарифмов), но при этом не являются рациональными.
Любое действительное число можно отобразить на числовой прямой:
Для перечисленных множеств чисел справедливо следующее выражение:
Т. е. множество натуральных чисел входит во множество целых чисел. Множество целых чисел входит во множество рациональных чисел. Множество рациональных чисел входит во множество действительных чисел. А множество действительных чисел входит во множество комплексных чисел.
Это высказывание можно проиллюстрировать с помощью кругов Эйлера: