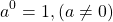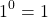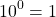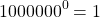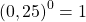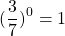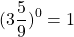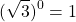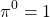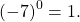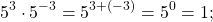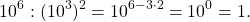число в какой степени будет равно 0

Степень 0

В алгебре возведение с нулевую степень встречается часто. Что такое степень 0? Какие числа можно возводить в нулевую степень, а какие — нет?

Любое число в нулевой степени, за исключением нуля, равно единице:

Таким образом, какое бы число ни возвели в степень 0, результат всегда получится одинаковый — единица.

И 1 в степени 0, и 2 в степени 0, и любое другое число — целое, дробное, положительное, отрицательное, рациональное, иррациональное — при возведении в нулевую степень дает единицу.

Единственное исключение — нуль.

Нуль в нулевой степени не определен, такое выражение не имеет смысла.

То есть в нулевую степень можно возводить любое число, кроме нуля.

Если при упрощении выражения со степенями получается число в нулевой степени, его можно заменить единицей:

Если при упрощении получается переменная или выражение с переменными в нулевой степени, пишем дополнительное условие — основание степени должно быть отличным от нуля:

Источник

Калькулятор степеней онлайн

Калькулятор степеней поможет просто и быстро возвести число в степень онлайн. При этом показатель степени может быть как положительным, так и отрицательным!

Что такое степень числа?

Число называется -ной степенью числа , если

то есть число равно числу умноженному само на себя раз.

Число обычно называют показателем степени, а число — основанием степени.

Как возвести число в степень?

Чтобы понять, как возводить число в степень, рассмотрим несколько простых примеров.

Пример. Вычислить степени и .

Решение. Возведём в пятую степень число то есть вычислим значение выражения По определению, данному выше,

Вычислим, чему равно то есть чему равно число возведённое в третью степень:

Отрицательный показатель степени

Показатели степени могут быть не только положительными, но и отрицательными.

Как пользоваться калькулятором степеней

Калькулятор помогает возводить число в степень онлайн. Основанием степени могут быть любые целые числа и десятичные дроби. Показатель степени тоже может быть любой десятичной дробью, однако следует помнить о том, что для отрицательных чисел не определена операция возведения в нецелую степень.

11 ответов к “Калькулятор степеней онлайн”

Какой полезный калькулятор! Обязательно буду заходить сюда, чтобы возвести в степень

Прикольный калькулятор. Спасибо разработчикам!

Кул работает и пользуюсь уже 2 года, спс вам

Я учусь в шестом классе и мне надо возводить число вместе с алгебраическими выражениями в степень для проверки плохо и очень не развито

Изи спасибочки. Подскажите пж как её только выучить!

Нужно было возвести 2 в степень 5344 он не смог

А может наоборот? Возвести 5344 в 2 степень? У меня получилось вот так: 28558336

вы серьёзно?) в 5344 степень? представляете, насколько огромным будет это число — сомневаюсь, что у вас была задача произвести данный расчёт)

Ради эксперимента проверил, какую максимальную степень двойки может посчитать этот калькулятор — оказалось 2 в степени 1023 =)

Если 2 возвести в 5344-ю степень, то получится 5061704973974027299980037235397513448048482008919929037452068511730689919393689275708195873247023710091624238976546252783172356964728778027673465208318699696248309328465552006571107620008402400316113976727105004411413170568376698638827973869411889908724226469194889717494331675235080420569385538265509961543067575194184368777022066111132302780134586762681814862556450431955406585448279703657841301874648667745383825070390933503110239608990830121654733661535454353270798145569384401850085642684868456528789562103761454957815426442747327711320324778931820919487682678321719643485487981589014549225510196642783819619040321611411359882004891658308371331596660870431184312167298846396164979001978798670288905053134295005836419677066694864628068689833081757033352953400571934965900129303051717534355229302033063952662005890103920130397669057188292338474776481357953030817758846266170223847929908504835302990531003462847503318950329743137236217543745914525444845087452846856657520414002727859280036714785859185037884951251727506875054813241209721227618995766654586418664166775992393835063979880053085295940327837196069147830766983986540597472451844237951115095179929576982740942980885130470892245479385543233307976981790695028656493961049492551311291706805115424750961587909791700885016992447022319410979439804631376542356654836900983639381662741245358906034504733868942797214559301686356660423072132482854337971020882585366350391567027791655093358398296246429557159392635530923149708329988109897525326946309383228095671339609631987990335561546054174382224932043330919578085565070532576355768067207797227163710652416

Источник

Числа. Степень числа.

То есть вместо умножения шести одинаковых множителей 5х5х5х5х5х5 пишут 5 6 и говорят «пять в шестой степени».

Действия, с помощью которых произведение равных множителей сворачивают в степень, называют возведением в степень.

В общем виде степень с основанием “a” и показателем “n” записывается так

Возвести число a в степень n – значит найти произведение n множителей, каждый из которых равен а

Если основание степени «а» равно 1, то значение степени при любом натуральном n будет равно 1. Например, 1 5 =1, 1 256 =1

Если возвести число «а» возвести в первую степень, то получим само число a: a 1 = a

Особыми считают вторую и третью степень числа. Для них придумали названия: вторую степень называют квадратом числа, третью – кубом этого числа.

-при нахождении степени положительного числа получается положительное число.

-при вычислениях нуля в натуральной степени получаем ноль.

– при вычислении степени отрицательного числа в результате может получиться как положительное число, так и отрицательное число. Это зависит от того чётным или нечётным числом был показатель степени.

Если решить несколько примеров на вычисление степени отрицательных чисел, то получится, что если мы вычисляем нечётную степень отрицательного числа, то в результате будет число со знаком минус. Так как при умножении нечётного количество отрицательных сомножителей получаем отрицательное значение.

Если же мы рассчитываем четную степень для отрицательного числа, то в результате будет положительное число. Так как при умножении чётного количества отрицательных сомножителей получаем положительное значение.

Свойства степени с натуральным показателем.

Чтобы умножить степени с одинаковыми основаниями мы основания не меняем, а показатели степеней складываем:

Чтобы разделить степени с одинаковыми основаниями основание не меняем, а показатели степеней вычитаем:

При расчетах возведения степени в степень основание не меняем, а показатели степеней умножаем друг на друга.

например: (2 3 ) 2 = 2 3·2 = 2 6

Если необходимо рассчитать возведение в степень произведения, то в эту степень возводится каждый множитель

При выполнении расчетов по возведению в степень дроби мы в данную степень возводим числитель и знаменатель дроби

Последовательность выполнения расчетов при работе с выражениями содержащими степень.

При выполнении расчетов выражений без скобок, но содержащих степени, в первую очередь производят возведение в степень, потом действия умножение и деление, и лишь потом операции сложения и вычитания.

Если необходимо вычислить выражение содержащие скобки, то сначала в указанном выше порядке делаем вычисления в скобках, а потом оставшиеся действия в том же порядке слева направо.

Очень широко в практических вычислениях для упрощения расчетов используют готовые таблицы степеней.

Источник

Свойства степеней. Действия со степенями

Что такое степень числа

В учебниках по математике можно встретить такое определение:

«Степенью n числа а является произведение множителей величиной а n-раз подряд»

a — основание степени

n — показатель степени

Соответственно, a n = a·a·a·a. ·a

Читается такое выражение, как a в степени n

Если говорить проще то, степень, а точнее показатель степени (n), говорит нам о том, сколько раз следует умножить это число (основание степени) на само себя.

А значит, если у нас есть задачка, где спрашивают, как возвести число в степень, например, число 2 — она решается довольно просто:

2 — основание степени

3 — показатель степени

Если вам нужно быстро возвести число в степень, можно использовать наш онлайн-калькулятор. Но чтобы не упасть в грязь лицом на контрольной по математике, придется все-таки разобраться с теорией.

Рассмотрим пример из жизни, чтобы было понятно, для чего можно использовать возведение чисел в степень на практике.

Задачка про миллион: представьте, что у вас есть миллион рублей. В начале каждого года вы зарабатываете на нем еще два. Получается, что миллион каждый год утраивается. Был один, а стало три — и так каждый год. Здорово, правда? А теперь посчитаем, какая сумма у вас будет через 4 года.

Как решаем: один миллион умножаем на три (1·3), затем результат умножаем на три, потом еще на три. Наверное, вам уже стало стало скучно, потому что вы поняли, что три нужно умножить само на себя четыре раза. Так и сделаем:

Математики заскучали и решили все упростить:

Ответ: через четыре года у вас будет 81 миллион.

Таблица степеней

Здесь мы приведем результаты возведения в степень натуральных чисел от 1 до 10 в квадрат (показатель степени два) и куб (показатель степени 3).

Источник

Таблица степеней

Основные понятия

Степень числа — это результат многократного умножения числа на себя. Само число называют основанием степени, а количество операций умножения — показателем степени.

Показатель степени всегда натуральное число — это значит, что его можно использовать при счете или перечислении предметов:

Запись читается, как «a» в степени «n».

Вот пример для наглядности:

Эту запись можно прочитать тремя способами:

Свойства степеней

Свойства степеней обычно используют, чтобы сократить или упростить сложные примеры. Удобно использовать вместе с таблицей степеней и таблицей умножения.

Таблица степеней от 1 до 10

Таблица степеней — это перечень чисел от 1 до 10 возведенных в степень от 1 до 10. Ниже приведены два вида таблиц, выберите ту, которая удобнее для вас — скачайте на телефон или распечатайте и положите в учебник.

Как найти необходимые значения в этой таблице:

В этой табличке мы просто ищем нужное нам число в степени и получаем ответ.

А если ответ нужно получить как можно быстрее, можно использовать онлайн калькулятор. Вот несколько подходящих:

Алгебра — предмет серьезный: при переходе в новый класс багаж формул и правил будет только увеличиваться. Поэтому важно запоминать все последовательно и практиковаться на примерах.

Решение задач

5 2 * 5 3 = 5 2+3 = 5 5 = 3125

2 4 * 3 3 * 2 5 = 2 4+5 * 3 3 = 2 9 * 3 3 = 512 * 27 = 13824

При условии, что у нас есть только таблица до 10, разложим основание степени на множители:

36 4 = 6 4 * 6 4 = 1296 * 1296 = 1679616

36 4 = 6 4 * 6 4 = 6 8 = 1679616

Бесплатный марафон: как самому создавать игры, а не только играть в них (◕ᴗ◕)

Записаться на марафон

Бесплатный марафон: как самому создавать игры, а не только играть в них (◕ᴗ◕)

Источник