что такое сложность алгоритма какая бывает
Введение в анализ сложности алгоритмов (часть 2)
От переводчика: данный текст даётся с незначительными сокращениями по причине местами излишней «разжёванности» материала. Автор абсолютно справедливо предупреждает, что отдельные темы могут показаться читателю чересчур простыми или общеизвестными. Тем не менее, лично мне этот текст помог упорядочить имеющиеся знания по анализу сложности алгоритмов. Надеюсь, что он окажется полезен и кому-то ещё.
Из-за большого объёма оригинальной статьи я разбила её на части, которых в общей сложности будет четыре.
Я (как всегда) буду крайне признательна за любые замечания в личку по улучшению качества перевода.
Сложность
Такой метод поиска значения внутри массива называется линейным поиском. Это обоснованное название, поскольку программа имеет f( n ) = n (что означает «линейный» более точно, мы рассмотрим в следующем разделе). Инструкция break позволяет программе завершиться раньше, даже после единственной итерации. Однако, напоминаю, что нас интересует самый неблагоприятный сценарий, при котором массив A вообще не содержит заданное значение. Поэтому f( n ) = n по-прежнему.
Давайте рассмотрим программу на Python, которая складывает два значения из массива и записывает результат в новую переменную:
Следующая программа на C++ проверяет, содержит ли вектор (своеобразный массив) A размера n два одинаковых значения:
Нотация «большое О»
В реальной жизни иногда проблематично выяснить точное поведение алгоритма тем способом, который мы рассматривали выше. Особенно для более сложных примеров. Однако, мы можем сказать, что поведение нашего алгоритма никогда не пересечёт некой границы. Это делает жизнь проще, так как чёткого указания на то, насколько быстр наш алгоритм, у нас может и не появиться, даже при условии игнорирования констант (как раньше). Всё, что нам нужно — найти эту границу, а как это сделать — проще объяснить на примере.
Наиболее известной задачей, которую используют при обучении алгоритмам, является сортировка. Даётся массив A размера n (звучит знакомо, не так ли?), и нас просят написать программу, его сортирующую. Интерес тут в том что, такая необходимость часто возникает в реальных системах. Например, обозревателю файлов нужно отсортировать файлы по имени, чтобы облегчить пользователю навигацию по ним. Или другой пример: в видеоигре может возникнуть задача сортировки 3D объектов, демонстрируемых на экране, по их расстоянию от точки зрения игрока в виртуальном мире. Цель: определить, какие из них будут для него видимы, а какие — нет (это называется Visibility Problem). Сортировка также интересна тем, что для неё существует множество алгоритмов, одни из которых хуже, чем другие. Так же эта задача проста для определения и объяснения. Поэтому давайте напишем кусок кода, который будет сортировать массив.
Перед вами совершенно неэффективный способ реализации сортировки массива на Ruby. (Конечно, Ruby поддерживает сортировку массивов с использованием встроенных функций, которые и следует использовать. Они несомненно быстрее, чем код выше, представленный исключительно для иллюстрации.)
Заметьте также, что хотя Ω и даёт нам нижний предел поведения нашей функции (т.е. мы улучшаем программу, чтобы она вычисляла меньшее количество инструкций), мы всё ещё ссылаемся на анализ наихудшего случая. Это происходит потому, что мы подаём на вход программы наихудший набор данных и анализируем её поведение.
В следующей таблице собраны символы, которые мы представили выше, и их связь с обычными математическими значками для сравнения чисел. Причина, по которой мы пользуемся греческими буквами вместо привычной математической нотации, в необходимости показать, что мы имеем дело со сравнением асимптотических оценок, а не с обычным.
| Оператор сравнения асимптотических оценок | Оператор сравнения чисел |
|---|---|
| Алгоритм является o( что-то ) | Число чего-то |
Анализ сложности алгоритмов. Примеры
Алгоритм — это точное предписание, однозначно определяющее вычислительный процесс, ведущий от варьируемых начальных данных к искомому результату [1].
При разработке алгоритмов очень важно иметь возможность оценить ресурсы, необходимые для проведения вычислений, результатом оценки является функция сложности (трудоемкости). Оцениваемым ресурсом чаще всего является процессорное время (вычислительная сложность) и память (сложность алгоритма по памяти). Оценка позволяет предсказать время выполнения и сравнивать эффективность алгоритмов.
Содержание:
Модель RAM (Random Access Machine)
Каждое вычислительное устройство имеет свои особенности, которые могут влиять на длительность вычисления. Обычно при разработке алгоритма не берутся во внимание такие детали, как размер кэша процессора или тип многозадачности, реализуемый операционной системой. Анализ алгоритмов проводят на модели абстрактного вычислителя, называемого машиной с произвольным доступом к памяти (RAM).
Модель состоит из памяти и процессора, которые работают следующим образом:
Несмотря на то, что такая модель далека от реального компьютера, она замечательно подходит для анализа алгоритмов. После того, как алгоритм будет реализован для конкретной ЭВМ, вы можете заняться профилированием и низкоуровневой оптимизацией, но это будет уже оптимизация кода, а не алгоритма.
Подсчет операций. Классы входных данных
Одним из способов оценки трудоемкости (\(T_n\)) является подсчет количества выполняемых операций. Рассмотрим в качестве примера алгоритм поиска минимального элемента массива.
При выполнении этого алгоритма будет выполнена:
Точное количество операций будет зависеть от обрабатываемых данных, поэтому имеет смысл говорить о наилучшем, наихудшем и среднем случаях. При этом худшему случаю всегда уделяется особое внимание, в том числе потому, что «плохие» данные могут быть намеренно поданы на вход злоумышленником.
Понятие среднего случая используется для оценки поведения алгоритма с расчетом на то, что наборы данных равновероятны. Однако, такая оценка достаточно сложна:
Асимптотические обозначения
Подсчет количества операций позволяет сравнить эффективность алгоритмов. Однако, аналогичный результат можно получить более простым путем. Анализ проводят с расчетом на достаточно большой объем обрабатываемых данных (\( n \to \infty \)), поэтому ключевое значение имеет скорость роста функции сложности, а не точное количество операций.
При анализе скорости роста игнорируются постоянные члены и множители в выражении, т.е. функции \(f_x = 10 \cdot x^2 + 20 \) и \( g_x = x^2\) эквивалентны с точки зрения скорости роста. Незначащие члены лишь добавляют «волнистости», которая затрудняет анализ.
В оценке алгоритмов используются специальные асимптотические обозначения, задающие следующие классы функций:
Запись \(f_n = \mathcal
Ограниченность функции g снизу функцией f записывается следующим образом: \(g_n =\Omega(f_n)\). Нотации \(\Omega\) и \(\mathcal

Если функции f и g имеют одинаковую скорость роста (\(f_n = \Theta(g_n)\)), то существуют положительные константы \(c_1\) и \(c_2\) такие, что \(\exists n_0 > 0 : \forall n > n_0, f_n \leq c_1 \cdot g_n, f_n \geq c_2 \cdot g_n\). При этом \(f_n = \Theta(g_n) \Leftrightarrow g_n = \Theta(f_n)\).

Примеры анализа алгоритмов
Алгоритм поиска минимального элемента массива, приведенный выше, выполнит N итераций цикла. Трудоемкость каждой итерации не зависит от количества элементов массива, поэтому имеет сложность \(T^
Алгоритм пузырьковой сортировки (bubble sort) использует два вложенных цикла. Во внутреннем последовательно сравниваются пары элементов и если оказывается, что элементы стоят в неправильном порядке — выполняется перестановка. Внешний цикл выполняется до тех пор, пока в массиве найдется хоть одна пара элементов, нарушающих требуемый порядок [2].
Трудоемкость функции swap не зависит от количества элементов в массиве, поэтому оценивается как \(T^
В алгоритме сортировки выбором массив мысленно разделяется на упорядоченную и необработанную части. На каждом шаге из неупорядоченной части массива выбирается минимальный элемент и добавляется в отсортированную часть [2].
Для поиска наименьшего элемента неупорядоченной части массива используется функция indMin, принимающая массив, размер массива и номер позиции, начиная с которой нужно производить поиск. Анализ сложности этой функции можно выполнить аналогично тому, как это сделано для функции min — количество операций линейно зависит от количества обрабатываемых элементов: \( T^
У сортировки выбором нет ветвлений, которые могут внести различия в оценку наилучшего и наихудшего случаев, ее трудоемкость: \(T^
Математический аппарат анализа алгоритмов
Выше были рассмотрены асимптотические обозначения, используемые при анализе скорости роста. Они позволяют существенно упростить задачу отбросив значительную часть выражения. Однако, в математическом анализе имеется целый ворох таких приемов.
Формулы суммирования
В примерах, рассмотренных выше, мы уже сталкивались с нетривиальными формулами суммирования. Чтобы дать оценку суммы можно использовать ряд известных тождеств:
Первые из этих тождеств достаточно просты, их можно вывести используя метод математической индукции. Если под знаком суммы стоит более сложная формула, как в двух последних тождествах — суммирование можно заменить интегрированием (взять интеграл функции гораздо проще, ведь для этого существует широкий спектр приемов).
Суммирование и интегрирование
Известно, что интеграл можно понимать как площадь фигуры, размещенной под графиком функции. Существует ряд методов аппроксимации (приближенного вычисления) интеграла, к ним относится, в частности, метод прямоугольников. Площадь под графиком делится на множество прямоугольников и приближенно вычисляется как сумма их площадей. Следовательно, возможен переход от интеграла к сумме и наоборот.
аппроксимация интеграла левыми прямоугольниками
аппроксимация интеграла правыми прямоугольниками
На рисунках приведен пример аппроксимации функции \(f_x = \log x\) левыми и правыми прямоугольниками. Очевидно, они дадут верхнюю и нижнюю оценку площади под графиком:
В частности, такой метод позволяет оценить алгоритмы, имеющие логарифмическую сложность (две последние формулы суммирования).
Сравнение сложности алгоритмов. Пределы
Сложность алгоритмов определяется для больших объемов обрабатываемых данных, т.е. при \(n\to\infty\). В связи с этим, при сравнении трудоемкости двух алгоритмов можно рассмотреть предел отношения функций их сложности: \(\lim\limits_
Если функции достаточно сложны, то такой прием значительно упрощает задачу, т.к. вместо предела отношения функций можно анализировать предел отношения их производных (согласно правилу Лопиталя): \(\lim\limits_
Допустим, требуется сравнить эффективность двух алгоритмов с оценками сложности \(\mathcal
Логарифмы и сложность алгоритмов. Пример
По определению \(\log_a
При анализе алгоритмов обычно встречаются логарифмы по основанию 2, однако основание не играет большой роли, поэтому зачастую не указывается. Последняя формула позволяет заменить основание логарифма, домножив его на константу, но константы отбрасываются при асимптотическом анализе.
Логарифмической сложностью обладают алгоритмы, для которых не требуется обрабатывать все исходные данные, они используют принцип «разделяй и властвуй». На каждом шаге часть данных (обычно половина) отбрасывается. Примером может быть функция поиска элемента в отсортированном массиве (двоичного поиска):
Очевидно, что на каждом шаге алгоритма количество рассматриваемых элементов сокращается в 2 раза. Количество элементов, среди которых может находиться искомый, на k-том шаге определяется формулой \(\frac
Результаты анализа. Замечания. Литература
Оценка сложности — замечательный способ не только сравнения алгоритмов, но и прогнозирования времени их работы. Никакие тесты производительности не дадут такой информации, т.к. зависят от особенностей конкретного компьютера и обрабатывают конкретные данные (не обязательно худший случай).
Анализ алгоритмов позволяет определить минимально возможную трудоемкость, например:
Нередко на собеседованиях просят разработать алгоритм с лучшей оценкой, чем возможно. Сами задачи при этом сводятся к какому-либо стандартному алгоритму. Человек, не знакомый с асимптотическим анализом начнет писать код, но требуется лишь обосновать невозможность существования такого алгоритма.
Alex tools
Алгоритмическая сложность
Процесс абстрагирования от деталей и определения скорости использования ресурсов с точки зрения размера ввода является одной из фундаментальных идей в информатике.
Асимптотические обозначения
Целью вычислительной сложности является классификация алгоритмов в соответствии с их производительностью. Мы представим функцию времени T(n), используя нотацию “big-O” для выражения сложности времени выполнения алгоритма. Например, следующее утверждение
говорит, что алгоритм имеет квадратичную сложность по времени.
Определение “big O”
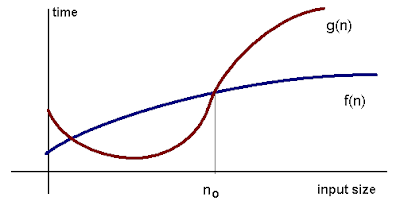
Для любых монотонных функций f(n) и g(n) от целых положительных чисел до целых положительных чисел говорят, что f(n) = O(g(n)), когда существуют такие константы c > 0 и n0 > 0, так что
Интуитивно это означает, что функция f(n) не растет быстрее, чем g(n), или что функция g(n) является верхней границей для f(n) для всех достаточно больших n → ∞
Вот графическое представление отношения f(n) = O(g(n)):
“big-O” нотация не симметрична: n = O(n2) но n2 ≠ O(n).
Постоянное время: O(1)
Говорят, что алгоритм работает за постоянное время, если ему требуется одинаковое количество времени независимо от размера ввода. Примеры:
Линейное время: O(n)
Говорят, что алгоритм работает за линейное время, если его выполнение по времени прямо пропорционально размеру ввода, то есть время увеличивается линейно с увеличением размера ввода. Примеры:
Логарифмическое время: O(log n)
Говорят, что алгоритм работает за логарифмическое время, если его время выполнения пропорционально логарифму размера ввода. Пример:
Обратите внимание, log(n)
Определение понятия “big Theta”
Чтобы измерить сложность конкретного алгоритма, нужно найти верхнюю и нижнюю границы. В этом случае используется новая запись. Мы говорим, что f(n) = Θ(g(n)) тогда и только тогда, когда f(n) = O(g(n)) и f(n) = Ω(g(n)). Примеры:
Анализ алгоритмов
Термин “анализ алгоритмов” используется для описания подходов к изучению производительности алгоритмов. Существуют следующие виды анализа:
Пример. Рассмотрим алгоритм последовательного поиска в массиве размером n.
Амортизированная временная сложность
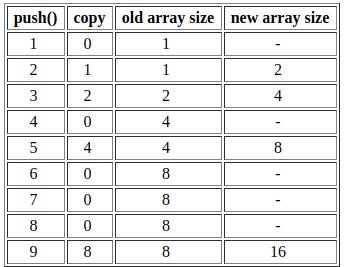
Рассмотрим стек динамических массивов. В этой модели push() удвоит размер массива, если места недостаточно. Поскольку копирование массивов не может быть выполнено в постоянное время, мы говорим, что push также не может быть сделан за постоянное время. В этом разделе мы покажем, что push() занимает амортизированное постоянное время.
Давайте посчитаем количество операций копирования, необходимых для выполнения последовательности push’ей.
Мы видим, что 3 push требуют 2 + 1 = 3 копирований.
Мы видим, что для 5 push требуется 4 + 2 + 1 = 7 копирований.
Мы видим, что для 9 push требуется 8 + 4 + 2 + 1 = 15 копирований.
Асимптотически количество копирований примерно равно количеству push.
В данном случае говорят, что алгоритм работает с амортизированным постоянным временем.
Сложность алгоритмов: О, о, Ω, Θ
В этой статье мы обсудим с Вами:
Помимо этого, мы рассмотрим сложность основных операций (if, for) и на примере Python-функции посчитаем сложность небольшого алгоритма.
Если Вы хотите получать еще больше интересных материалов по программированию, Data Science и математике, то подписывайтесь на нашу группу ВК, канал в Телеграме и Инстаграм. Каждый день мы публикуем полезный контент и вопросы с реальных собеседований.
О большое, O малое, Омега и Тета
Существует 4 нотации для описания поведения функций относительно друг друга. Давайте разберемся с каждой из них.
Формальные математические определения этих нотаций следующие:
Теперь стало понятнее, что означают записи f(x) = O(g(x)) и f(x) = о(g(x)). Конечно, эти определения еще осмыслить нужно, но хотя бы термины «доминирует» и «растет не быстрее» дают надежду на понимание 🙂
Однако теперь в игру вступают еще две нотации: Омега и Тета.
Посмотрим на графиках, как ведут себя функции.
На первом графике мы наблюдаем, что с увеличением значения n функция f(n) растет медленней cg(n). То есть функция f(n) ограничена сверху функцией cg(n), а значит f = O(g).
На третьем графика функция f(n) зажата между c1g(n) и c2g(n), то есть ограничена и сверху и снизу. Это и есть иллюстрация тетта-нотации.
Сложность алгоритмов
Пример: если мы увеличим количество входных данных (допустим, размер массива) в 10 раз, во сколько раз вырастет количество операций? В 10? В 100? А может в 2 или 20? Именно такую оценку и позволяет дать описание сложности алгоритма.
Для начала посмотрим на сложность, описываемую разными функциями.
На диаграмме цветом выделены классы сложности.
1. O(1) имеет наименьшую сложность
Алгоритм с таким классом сложности не зависит от размера входных данных. Если вы можете создать алгоритм для решения проблемы с O(1), то это будет наилучший выбор. Такую сложность имеет, например, операция вставки элемента в односвязный список.
2. O(log(n)) является более сложным, чем O(1), но менее сложным, чем полиномы
3. Сложность многочленов увеличивается с ростом степени
Например, алгоритмы со сложностью O(n^6) являются более сложными, чем O(n^2). Примером алгоритма с квадратичной сложностью служит алгоритм сортировки вставками, т.к. он подразумевает 2 вложенных цикла.
4. Показательные функции имеют большую сложность, чем полиномы.
5. Факториалы имеют самую большую сложность
Факториальная временная сложность — это когда количество вычислений в алгоритме прирастает факториально в зависимости от размера набора данных. Примером может служить рекурсивная функция расчета факториала.
Разобравшись со сложностью отдельных операций мы переходим к их комбинированию, потому что без этого более-менее сложный алгоритм мы оценить не сможем.
Закон сложения для O-нотации
При сложении двух классов сложности складываются функции этих классов. Однако, O(f(n) + g(n)) приводит нас к большему из двух исходных классов – так как меньший член выражения просто отбрасывается.
так как N растет быстрее, чем log N.
Это правило позволяет вычислить класс сложности для последовательности операций. Например, сначала мы выполняем выражение со сложностью O(f(n)), а следом за ним – O(g(n)). Тогда выполнение обоих выражений (одно за другим) будет иметь сложность O(f(n)) + O(g(n)), то есть O(f(n) + g(n)).
Пример
Вызов функции fun1(. ) имеет сложность O(N), а вызов fun2(. ) – O (N * log N). Вызываем эти функции друг за другом.
Сложность этого действия будет равна:
Если мы вызовем функцию fun1(. ) дважды, то получим:
Константа 2 в вычислениях отбрасывается.
Условия
Отдельно разберем выполнение условий (if). Сначала выполняется само условие, а затем один из блоков (if или else).
Предположим, что вычисление условия test имеет сложность O(T), блока block 1 – O(B1), а блока block 2 – O(B2).
Тогда сложность всего кода будет равна:
Подставим реальные значения:
и вычислим сложность кода:
Если бы операция test имела класс сложности O(N^3), то общая сложность кода составила бы O(N^3).
В O-нотации мы всегда отбрасываем менее значимые элементы.
Закон умножения для O-нотации
Если мы повторяем N раз некоторый процесс с классом сложности O(f(N)), то результирующий класс сложности будет равен:
Предположим, некоторая функция f(. ) имеет класс сложности O(N^2). Выполним ее в цикле N раз:
Сложность этого кода будет равна:
Это правило позволяет вычислять класс сложности для выполнения некоторого повторяющегося несколько раз выражения. Необходимо умножить количество повторений на класс сложности самого выражения.
Расчет сложности алгоритмов на Python
Давайте посчитаем сложность на примере простого алгоритма на языке Python, чтобы лучше понимать процесс вычисления.
Возьмем код, который определяет, состоит ли список из уникальных значений (т.е. нет ли в нем дубликатов). Размер списка обозначим как N, а сложность операции сравнения элементов примем за O(1).
Список уникален, если каждое его значение не встречается ни разу «справа» от элемента. Для значения alist[i] «правым» фрагментом списка будет срез alist[i+1:].
Определим сложность для каждой строки функции:
Таким образом, полная сложность цикла (по ранее рассмотренному нами правилу) равна:
Если размер списка увеличится вдвое, то выполнение функции займет в 4 раза больше времени.
Эпилог
Итак, давайте подведем итог, что же мы узнали:
Основные правила расчета сложности алгоритмов:
Сложность блока if рассчитывается так: условие выполняется всегда, а затем один из блоков. Для расчета максимальной сложности предполагаем, что выполняется самый сложный блок:
Сложность блока for рассчитывается просто: количество индексов умножается на сложность вычисления индекса и на сложность самой функции в цикле.
Вот мы и разобрали с Вами основные положения расчета сложности алгоритмов. При этом теперь Вы будете не просто правильно определять сложность, а понимать математическую основу этого процесса.
Если Вы хотите получать еще больше интересных материалов по программированию, Data Science и математике, то подписывайтесь на нашу группу ВК, канал в Телеграме и Инстаграм. Каждый день мы публикуем полезный контент и вопросы с реальных собеседований.