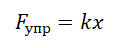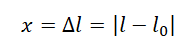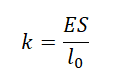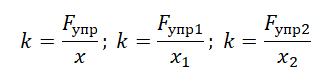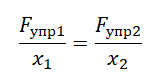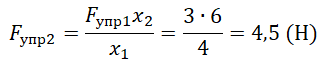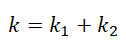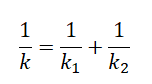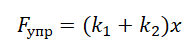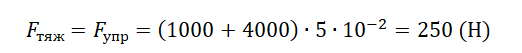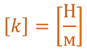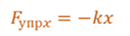что такое жестокость тела при каких деформациях
Сила упругости
Сила: что это за величина
В повседневной жизни мы часто встречаем, как любое тело деформируется (меняет форму или размер), ускоряется или тормозит, падает. В общем, чего только с разными телами в реальной жизни не происходит. Причиной любого действия или взаимодействия является сила.
Сила — это физическая векторная величина, которую воздействует на данное тело со стороны других тел.
Она измеряется в Ньютонах — это единица измерения названа в честь Исаака Ньютона.
Сила — величина векторная. Это значит, что, помимо модуля, у нее есть направление. От того, куда направлена сила, зависит результат.
Вот стоите вы на лонгборде: можете оттолкнуться вправо, а можете влево — в зависимости от того, в какую сторону оттолкнетесь, результат будет разный. В данном случае результат выражается в направлении движения.
Деформация
Деформация — это изменение формы и размеров тела (или части тела) под действием внешних сил
Происходит деформация из-за различных факторов: при изменении температуры, влажности, фазовых превращениях и других воздействиях, вызывающих изменение положения частиц тела.
Деформация является деформацией, пока сила, вызывающая эту деформацию, не приведет к разрушению.
На появление того или иного вида деформации большое влияние оказывает характер приложенных к телу напряжений. Одни процессы деформации связаны с преимущественно перпендикулярно (нормально) приложенной силой, а другие — преимущественно с силой, приложенной по касательной.
По характеру приложенной к телу нагрузки виды деформации подразделяют следующим образом:
Сила упругости: Закон Гука
Деформацию тоже можно назвать упругой (при которой тело стремится вернуть свою форму и размер в изначальное состояние) и неупругой (когда тело не стремится вернуться в исходное состояние).
При деформации возникает сила упругости— это та сила, которая стремится вернуть тело в исходное состояние, в котором оно было до деформации.
Сила упругости, возникающая при упругой деформации растяжения или сжатия тела, пропорциональна абсолютному значению изменения длины тела. Выражение, описывающее эту закономерность, называется законом Гука.
Закон Гука
Fупр = kx
Fупр — сила упругости [Н]
k — коэффициент жесткости [Н/м]
х — изменение длины (деформация) [м]
Изменение длины может обозначаться по-разному в различных источниках. Варианты обозначений: x, ∆x, ∆l.
Это равноценные обозначения — можно использовать любое удобное.
Поскольку сила упругости направлена против направления силы, с которой это тело деформируется (она же стремится все «распрямить»), в Законе Гука должен быть знак минус. Часто его и можно встретить в разных учебниках. Но поскольку мы учитываем направление этой силы при решении задач, знак минус можно не ставить.
Задачка
На сколько удлинится рыболовная леска жесткостью 0,3 кН/м при поднятии вверх рыбы весом 300 г?
Решение:
Сначала определим силу, которая возникает, когда мы что-то поднимаем. Это, конечно, сила тяжести. Не забываем массу представить в единицах СИ – килограммах.
Если принять ускорение свободного падения равным 10 м/с*с, то модуль силы тяжести равен :
Тогда из Закона Гука выразим модуль удлинения лески:
Выражаем модуль удлинения:
Подставим числа, жесткость лески при этом выражаем в Ньютонах:
x=3/(0,3 * 1000)=0,01 м = 1 см
Ответ: удлинение лески равно 1 см.
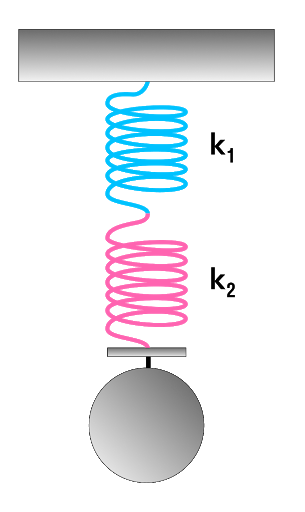
Параллельное и последовательное соединение пружин
В Законе Гука есть такая величина, как коэффициент жесткости— это характеристика тела, которая показывает его способность сопротивляться деформации. Чем больше коэффициент жесткости, тем больше эта способность, а как следствие из Закона Гука — и сила упругости.
Чаще всего эта характеристика используется для описания жесткости пружины. Но если мы соединим несколько пружин, то их суммарная жесткость нужно будет рассчитать. Разберемся, каким же образом.
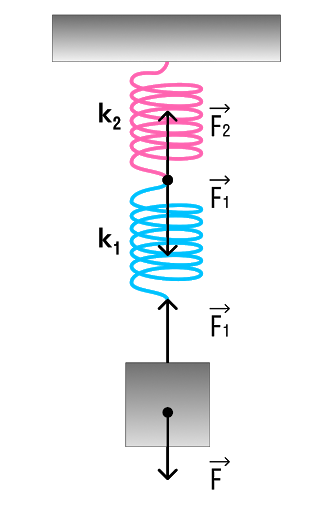
Последовательное соединение системы пружин
Последовательное соединение характерно наличием одной точки соединения пружин.
При последовательном соединении общая жесткость системы уменьшается. Формула для расчета коэффициента упругости будет иметь следующий вид:
Коэффициент жесткости при последовательном соединении пружин
1/k = 1/k₁ + 1/k₂ + … + 1/k_i
k — общая жесткость системы [Н/м] k1, k2, …, — отдельные жесткости каждого элемента [Н/м] i — общее количество всех пружин, задействованных в системе [-]
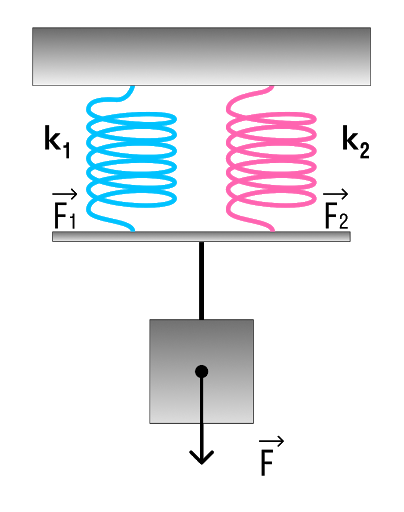
Параллельное соединение системы пружин
Последовательное соединение характерно наличием двух точек соединения пружин.
В случае когда пружины соединены параллельно величина общего коэффициента упругости системы будет увеличиваться. Формула для расчета будет выглядеть так:
Коэффициент жесткости при параллельном соединении пружин
k — общая жесткость системы [Н/м] k1, k2, …, ki — отдельные жесткости каждого элемента [Н/м] i — общее количество всех пружин, задействованных в системе [-]
Задачка
Какова жесткость системы из двух пружин, жесткости которых k₁ = 100 Н/м, k₂ = 200 Н/м, соединенных: а) параллельно; б) последовательно?
Решение:
а) Рассмотрим параллельное соединение пружин.
При параллельном соединении пружин общая жесткость
k = k₁ + k₂ = 100 + 200 = 300 Н/м
б) Рассмотрим последовательное соединение пружин.
При последовательном соединении общая жесткость двух пружин
1/k = 1/100 + 1/200 = 0,01 + 0,005 = 0,015
k = 1000/15 = 200/3 ≃ 66,7 Н/м
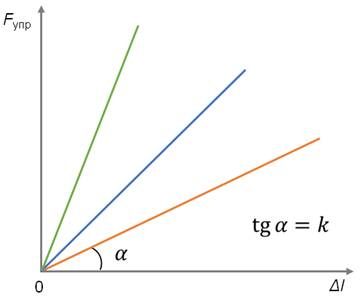
График зависимости силы упругости от жесткости
Закон Гука можно представить в виде графика. Это график зависимости силы упругости от изменения длины и по нему очень удобно можно рассчитать коэффициент жесткости. Давай рассмотрим на примере задач.
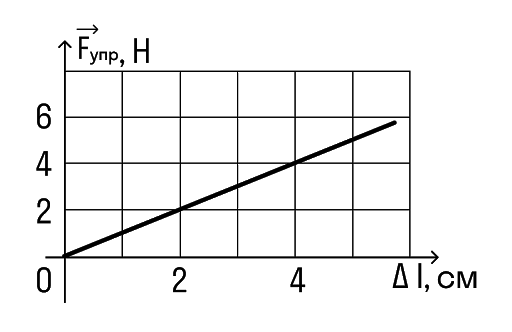
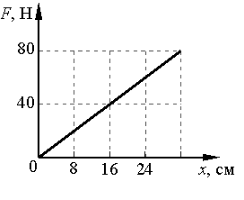
Задачка 1
Определите по графику коэффициент жесткости тела.
Решение:
Из Закона Гука выразим коэффициент жесткости тела:
Снимем значения с графика. Важно выбрать одну точку на графике и записать для нее значения обеих величин.
Например, возьмем вот эту точку.
В ней удлинение равно 2 см, а сила упругости 2 Н.
Переведем сантиметры в метры: 2 см = 0,02 м И подставим в формулу: k = F/x = 2/0,02 = 100 Н/м
Ответ:жесткость пружины равна 100 Н/м
Задачка 2
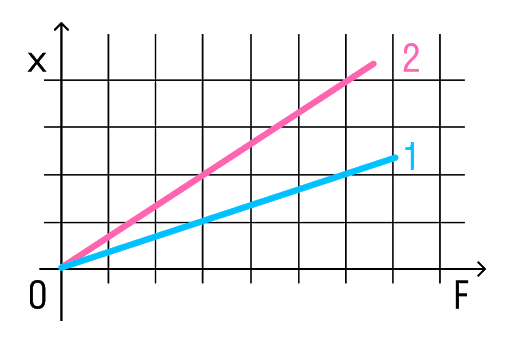
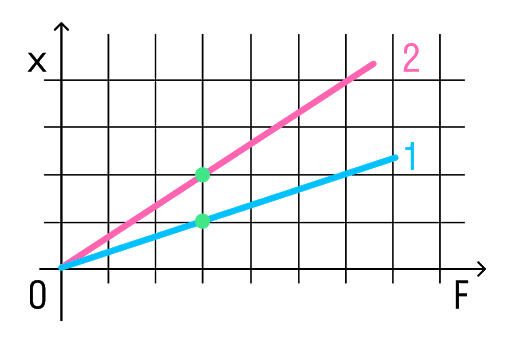
На рисунке представлены графики зависимости удлинения от модуля приложенной силы для стальной (1) и медной (2) проволок равной длины и диаметра. Сравнить жесткости проволок.
Решение:
Возьмем точки на графиках, у которых будет одинаковая сила, но разное удлинение.
Мы видим, что при одинаковой силе удлинение 2 проволоки (медной) больше, чем 1 (стальной). Если выразить из Закона Гука жесткость, то можно увидеть, что она обратно пропорциональна удлинению.
Значит жесткость стальной проволоки больше.
Ответ: жесткость стальной проволоки больше медной.
Бесплатный марафон: как самому создавать игры, а не только играть в них (◕ᴗ◕)
Записаться на марафон
Бесплатный марафон: как самому создавать игры, а не только играть в них (◕ᴗ◕)
Деформация и силы упругости. Закон Гука
Урок 16. Физика 10 класс ФГОС
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока “Деформация и силы упругости. Закон Гука”
При рассмотрении понятия «сила» мы с вами говорили о том, что она является количественной мерой воздействия одного тела на другое, в результате которого тела приобретают ускорения или деформируются.
Мы уже с вами знаем, что такое ускорение тела. А теперь давайте вспомним, что такое деформация. Итак, под деформацией понимают изменение формы или объёма одного тела в результате воздействия на него другого тела.
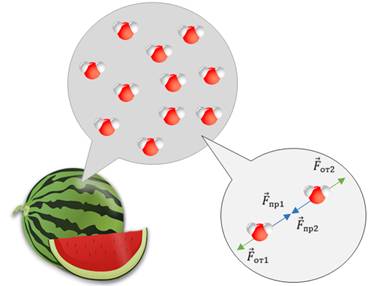
Возникновение в теле деформаций объясняется дискретным строением вещества. Ещё в восьмом классе мы говорили о том, что все вещества состоят из мельчайших частиц, разделённых между собой промежутками. Между этими частицами существуют силы взаимодействия электромагнитной природы.
В зависимости от расстояния между частицами они проявляются то как силы притяжения, то как силы отталкивания. Например, когда воздействие на тело вызывает увеличение расстояния между молекулами, то силы межмолекулярного притяжения препятствуют этому. Уменьшению же расстояния между молекулами противодействуют силы отталкивания. Так вот, чтобы не рассматривать сложные электромагнитные взаимодействия между отдельными частицами вещества, в механике для характеристики этих явлений и вводят силу упругости.
Силами упругости называются силы, возникающие при деформации любых твёрдых тел, а также при сжатии жидкостей и газов. Они препятствуют изменению объёма и формы тела.
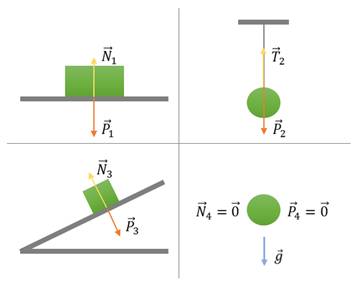
Обратим ваше внимание на то, что силы упругости приложены к телу, которое вызывает деформацию, и всегда направлены противоположно деформирующей силе перпендикулярно поверхности соприкосновения взаимодействующих тел. А если во взаимодействии участвуют такие тела, как пружины или нити, то силы упругости направлены вдоль их оси́.
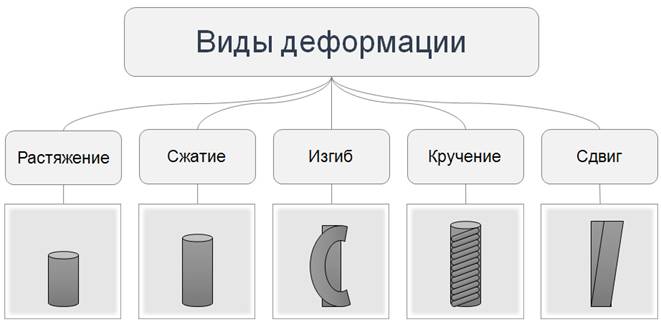
По характеру смещения молекулярных слоёв внутри тела друг относительно друга различают несколько видов деформации. Так, если расстояние между слоями увеличивается, то говорят о деформации растяжения. Если же, наоборот, уменьшается, то это деформация сжатия.
Деформация, при которой происходит взаимное смещение параллельных молекулярных слоёв под воздействием деформирующей силы, называется деформацией сдвига.
Когда в разных частях тела возникают неодинаковые комбинации растяжения и сжатия, то это деформация изгиба.
А различные комбинации деформаций сдвига проявляются как деформация кручения.
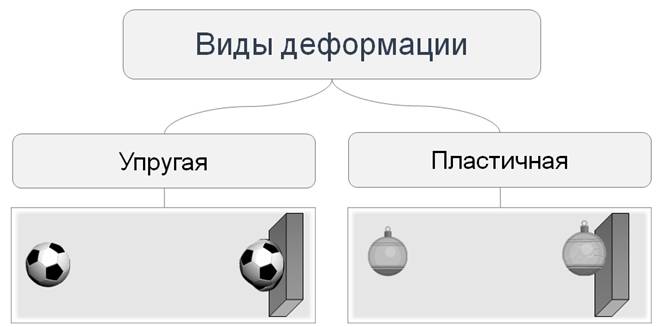
Также принято различать упругие деформации и неупругие, или пластичные.
Деформация называется упругой, если после прекращения воздействия тело полностью восстанавливает первоначальные форму и размеры.
А если этого не происходит, то деформация называется пластичной.
Чаще всего мы с вами сталкиваемся с упругими деформациями растяжения или сжатия. Первое по-настоящему научное исследование этих процессов предпринял Роберт Гук в 1660 году. Он экспериментально установил, что при малых деформациях растяжения или сжатия абсолютное удлинение тела прямо пропорционально деформирующей силе.
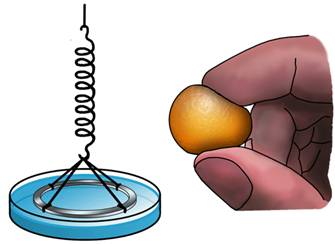
Проверим это. Возьмём длинную рейку, к которой прикреплены четыре абсолютно одинаковых резиновых шнура. Крайний левый мы будем использовать в качестве эталона. Подвесим ко второму шнуру́ груз известной массы. Под действием его веса шнур растянется и, следовательно, в нём возникнет сила упругости. Она, согласно третьему закону Ньютона, будет равна по модулю и противоположна по направлению весу тела. А величина удлинения шнура, также называемая абсолютным удлинением, равна разности между его конечной и начальной длиной.
Для третьего шнура увеличим нагрузку в два раза, подвесив на него два одинаковых груза. Шнур растянулся сильнее. При этом видно, что удлинение шнура выросло в два раза. Наконец, подвесим к последнему шнуру три одинаковых груза. Удлинение шнура выросло в три раза.
Таким образом, действительно, при малых упругих деформациях растяжения или сжатия модуль силы упругости прямо пропорционален абсолютному удлинению тела:
В этом и состоит экспериментально установленный закон Гука.
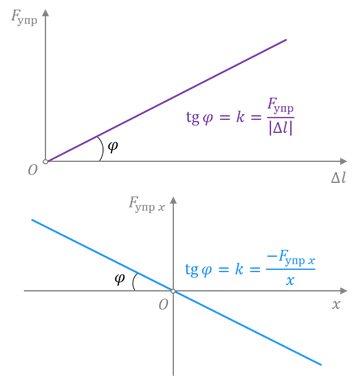
При решении большинства задач необходимо помнить, что сила упругости — это всё-таки векторная величина, то есть она имеет направление. Тогда, если выбрать начало отсчёта под крайней точкой недеформированного тела, то абсолютное удлинение можно характеризовать координатой конца деформированного тела. А так как координата и проекция силы упругости деформированного тела на ось координат имеют противоположные знаки, то закон Гука в проекциях на выбранную ось запишется в виде:
Коэффициент пропорциональности, входящий в формулу, называют коэффициентом упругости или жёсткостью тела. Она численно равна модулю силы упругости при удлинении (или сжатии) тела на единицу длины.
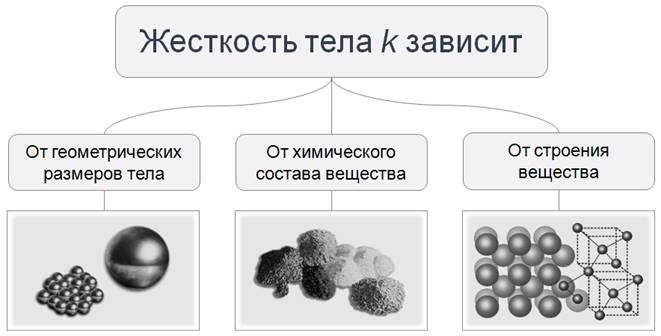
Следует также отметить, что жёсткость является характеристикой данного тела, которая зависит от многих факторов и в частности: от материала, из которого изготовлено тело, его продольных и поперечных размеров, химического состава и строения вещества, а также от температуры тела.
Графиком зависимости модуля силы упругости от абсолютного удлинения тела является прямая линия, угол наклона которой к оси абсцисс зависит от коэффициента жёсткости.
В заключение отметим, что сила упругости, как и любая из сил, рассматриваемых в механике, подчиняется законам Ньютона. А по закону Гука можно рассчитать деформации, возникающие при взаимодействиях тел. Однако необходимо помнить, что закон Гука хорошо выполняется только для упругих деформаций, при которых удлинение тела мало́. А также при рассмотрении деформаций в упругой пружине.
Сила упругости и закон Гука
теория по физике 🧲 динамика
Сила упругости — сила, которая возникает при деформациях тел в качестве ответной реакции на внешнее воздействие. Сила упругости имеет электромагнитную природу.
Деформация — изменение формы или объема тела.
Сила упругости обозначается как F упр. Единица измерения — Ньютон (Н). Сила упругости направлена противоположно перемещению частиц при деформации.
Если после окончания действия внешних сил тело возвращает прежние форму и объем, то деформацию и само тело называю упругими. Если после окончания действия внешних сил тело остается деформированным, то деформацию и само тело называют пластическими, или неупругими.
Примеры упругой деформации:
Примеры пластической деформации:
Закон Гука
При упругой деформации есть взаимосвязь между силой упругости, возникающей в результате деформации, и удлинением деформируемого тела. Эту взаимосвязь первым обнаружил английский ученый Роберт Гук.
Модуль силы упругости, возникающей при деформации тела, пропорционален его удлинению.
x — абсолютное удлинение (деформация), k — коэффициент жесткости тела.
Абсолютное удлинение определяется формулой:
l0 — начальная длина тела, l — длина деформированного тела, ∆l — изменение длины тела.
Коэффициент жесткости тела определяется формулой:
E — модуль упругости (модуль Юнга). Каждое вещество обладает своим модулем упругости. S — площадь сечения тела.
Важно! Закон Гука не работает в случае, если деформация была пластической.
Пример №1. Под действием силы 3Н пружина удлинилась на 4 см. Найти модуль силы, под действием которой удлинение пружины составит 6 см.
Согласно третьему закону Ньютона модуль силы упругости будет равен модулю приложенной к пружине силе. В обоих случаях постоянной величиной окажется только жесткость пружины. Выразим ее из закона Гука и применим к каждому из случаев:
Приравняем правые части формул:
Выразим и вычислим силу упругости, возникающую, когда удлинение пружины составит 6 см:
Если пружину растягивают две противоположные силы, то модули силы упругости и модули этих сил равны между собой:
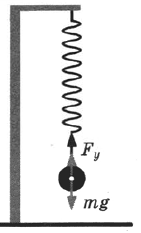
Если груз подвешен к пружине, сила упругости будет равна силе тяжести, действующей на это тело:
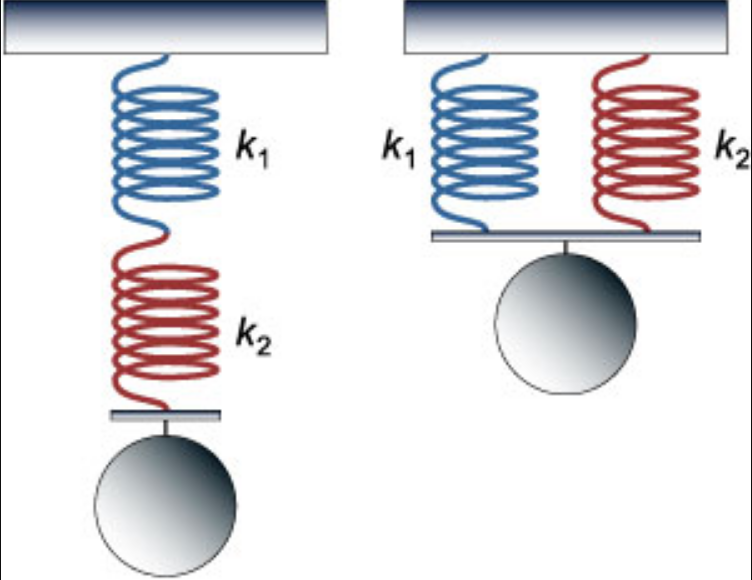
Если пружины соединены параллельно, их суммарный коэффициент жесткости будет равен сумме коэффициентов жесткости каждой из этих пружин:
Если пружины соединены последовательно, их обратное значение суммарного коэффициента жесткости будет равен сумме обратных коэффициентов жесткости для каждой из пружин:
Пример №2. Две пружины соединены параллельно. Жесткость одной из пружин равна 1000 Нм, второй — 4000 Нм. Когда к пружинам подвесили груз, они удлинились на 5 см. Найти силу тяжести груза.
Переведем сантиметры в метры: 5 см = 5∙10 –2 м.
Запишем закон Гука с учетом параллельного соединения пружин:
Модуль силы тяжести согласно третьему закону Ньютона равен модулю силы упругости. Отсюда:
Дополнительным понятием является гибкость или податливость: чем более гибкий объект, тем он менее жесткий.
СОДЕРЖАНИЕ
Расчеты
Следует отметить, что для тела с несколькими степенями свободы вышеупомянутое уравнение обычно не применяется, поскольку приложенная сила создает не только отклонение в своем собственном направлении (или степени свободы), но также и в других направлениях.
Для тела с несколькими степенями свободы, чтобы вычислить конкретную прямую жесткость (диагональные члены), соответствующая степень свободы остается свободной, а остальные должны быть ограничены. При таком условии, приведенное выше уравнение можно использовать для получения жесткости, напрямую связанной с неограниченной степенью свободы. Соотношения между силами реакции (или моментами) и произведенным прогибом представляют собой жесткости соединения.
Согласие
Вращательная жесткость
На аналогичной основе выводятся и другие меры жесткости, в том числе:
Отношение к эластичности
Точно так же жесткость прямого участка на кручение равна
Обратите внимание, что жесткость на кручение имеет размеры [сила] * [длина] / [угол], так что в системе СИ единицами измерения являются Н * м / рад.
В частном случае неограниченного одноосного растяжения или сжатия модуль Юнга можно рассматривать как меру жесткости конструкции.
Приложения
Сила упругости. Закон Гука
Урок 18. Подготовка к ЕГЭ по физике. Часть 1. Механика.
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока “Сила упругости. Закон Гука”
В данной теме речь пойдёт о силах упругости, а также о законе Гука.
Ранее говорилось, что основными силами в механике являются гравитационные силы, силы упругости и силы трения.
Известно, что одно из проявлений взаимодействия тел — это их деформация. Деформацией называют изменение формы и размеров тела, происходящее из-за неодинакового смещения различных частей одного тела в результате воздействия другого тела.
Рассмотрим, почему деформации неодинаковы у различных тел?
Чтобы ответить на этот вопрос, вспомним о строении вещества. Все вещества состоят из частиц (молекул, атомов, ионов), между которыми существуют силы взаимодействия. Это силы электромагнитной природы, которые в зависимости от расстояния между частицами проявляются то как силы притяжения, то как силы отталкивания. Если воздействие на тело вызывает увеличение расстояния между молекулами, то силы межмолекулярного притяжения препятствуют этому. Уменьшению расстояния между молекулами противодействуют силы отталкивания. Так вот, чтобы не рассматривать сложные электромагнитные взаимодействия, в механике для характеристики этих явлений и вводят силу упругости.
Силой упругости называется сила, возникающая при деформации любых твердых тел, а также при сжатии жидкостей и газов. Сила упругости препятствует изменению размеров и формы тела.
Также следует помнить, что силы упругости всегда перпендикулярны поверхности соприкосновения взаимодействующих тел, а если во взаимодействии участвуют такие тела, как пружины или нити, то силы упругости направлены вдоль их оси.
Рассмотрим, какую роль играет эта сила при взаимодействии тел. Проведём следующий опыт. Прикрепим к бруску, лежащему на столе, резиновый шнур (с метками на одинаковом расстоянии друг от друга) и медленно начнем тянуть его в горизонтальном направлении. Под действием силы шнур растягивается, и только когда весь шнур растянется на некоторую величину, брусок придет в движение. Как это объяснить?
При растяжении шнура происходит смещение одних его частей относительно других, в результате чего в шнуре возникает сила упругости, равная по величине деформирующей силе. С этого момента шнур играет роль «передающего звена». Такие же явления всегда происходят, когда движение от одного тела к другому передается при помощи «связей», то есть нитей, шнуров, пружин, тросов, различных сцепок и так далее.
По характеру смещения частей тела (а вернее, молекулярных слоев внутри него) друг относительно друга различают несколько видов деформации: растяжение, сжатие, изгиб, кручение, сдвиг.
При деформации растяжения расстояние между молекулярными слоями увеличивается. Такую деформацию испытывают, например, тросы подъемных кранов, канатных дорог, буксирные тросы, струны музыкальных инструментов.
А при деформации сжатия расстояние между молекулярными слоями уменьшается. Сжатию, например, подвергаются стены и фундаменты зданий.
Если в результате воздействия одни молекулярные слои растягиваются, а другие сжимаются, то наблюдается деформация изгиба. Деформацию изгиба испытывают на себе балки перекрытий в зданиях и мостах.
При деформации кручения происходит поворот одних молекулярных слоев относительно других. А если одни слои молекул смещаются относительно других, то происходит деформация сдвига.
По мимо этого, деформации также разделяют на упругие и неупругие, или пластичные.
Деформация называется упругой, если после прекращения воздействия тело полностью восстанавливает первоначальные форму и размеры.
А если этого не происходит, то деформация называется неупругой или пластичной.
Конечно же, деформация конкретного тела может быть, как упругой, так и неупругой, так как ее характер зависит не только от свойств тела, но и от величины воздействия на него.
Различные виды деформаций возникают в любых сооружениях и механизмах, и необходимо установить законы, которые позволят рассчитать величину этих деформаций.
Наиболее часто встречаются и достаточно просто математически описываются упругие деформации растяжения или сжатия.
Если взаимодействие этих тел друг с другом ничем не отличается, то каково ускорение третьего тела при его взаимодействии с одним из первых двух?
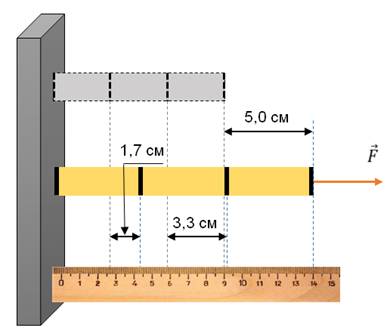
Проведем опыт. Прикрепим один конец резинового шнура с метками к вертикальной стенке, а другой — к динамометру, на который будем действовать силой. Расположим под шнуром линейку. Определяя силу, действующую на конец шнура, по динамометру, будем фиксировать смещение конца шнура вдоль линейки и изменение расстояний между метками.
Общее удлинение шнура, определяемое по смещению его конца, является суммой удлинений всех его частей. Аналогично общее укорочение, например, при сжатии пружины, является суммой уменьшений расстояний между всеми ее витками.
Если обозначить начальную длину шнура через l0, а конечную длину — через l, то для характеристики деформаций растяжения или сжатия можно ввести абсолютное удлинение ∆l, равное модулю разности между конечной и начальной длиной тела.
Если шнур под действием деформирующей силы больше не удлиняется, то ее действие уравновешивает упругая сила.
Первое по-настоящему научное исследование процесса упругого растяжения и сжатия вещества предпринял Роберт Гук. Он установил экспериментально, что при малых деформациях растяжения или сжатия абсолютное удлинение тела прямо пропорционально деформирующей силе.
На практике часто необходимо определить силу упругости, возникающую в теле при его деформации, и закон Гука формулируют следующим образом: модуль силы упругости, возникающей при малых деформациях сжатия или растяжения тела, прямо пропорционален величине абсолютного удлинения.
где k — это коэффициент пропорциональности, называемый жесткостью тела.
Жесткость является характеристикой данного тела (пружины, шнура, стержня) и зависит от его поперечных и продольных размеров, химического состава, и строения вещества, из которого тело изготовлено.
Единицей измерения жесткости в системе СИ, является Н/м (ньютон на метр).
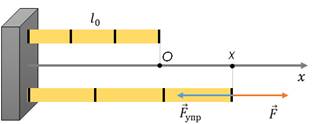
При расчетах движения тел под действием силы упругости необходимо учитывать ее направление. Если выбрать начало отсчета под крайней точкой недеформированного тела, то абсолютное удлинение можно характеризовать координатой конца деформированного тела.
При растяжении и при сжатии образца сила упругости направлена противоположно смещению его конца. Тогда можно записать закон Гука для проекции силы упругости на выбранную координатную ось в виде:
Ту или иную форму записи закона Гука используют в зависимости от условия задачи и величины, которую нужно определить.
Графиком зависимости силы упругости от абсолютного удлинения тела является прямая линия, угол наклона которой к оси абсцисс зависит от коэффициента жесткости k.
Сила упругости, как и любая из сил, рассматриваемых в механике, подчиняется законам Ньютона, а по закону Гука можно рассчитать деформации, возникающие при взаимодействиях тел. Однако необходимо отметить, что закон Гука хорошо выполняется только при малых деформациях.
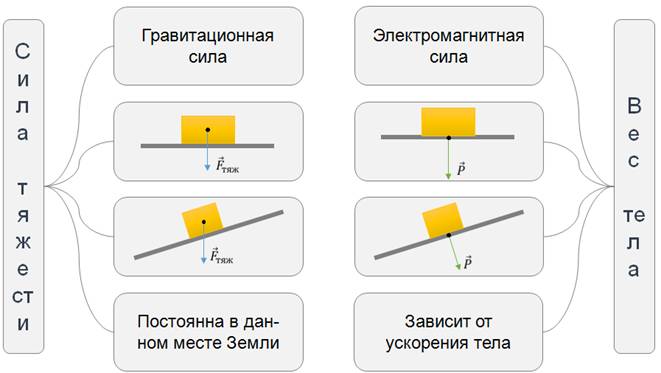
Частным случаем проявления силы упругости является вес тела. Вес тела — это сила, с которой тело, вследствие своего притяжения к Земле, действует на неподвижную относительно него опору или подвес.
Вес тела возникает вследствие его деформации, вызванной действием силы со стороны опоры (силы нормальной реакции опоры) или подвеса (силы натяжения).
Следует помнить, что сила веса существенно отличается от силы тяжести. Во-первых, вес тела обусловлен силой тяготения и межмолекулярными силами в веществе, то есть это сила электромагнитной природы. А сила тяжести — это гравитационная сила.
Во-вторых, они приложены к разным телам: сила тяжести приложена к телу, а вес — к опоре или подвесу.
В-третьих, направление силы веса тела не обязательно совпадает с отвесным направлением.
Сила тяжести, действующая на тело в данном месте Земли постоянна, и не зависит от характера движения тела. Вес зависит от ускорения, с которым движется тело.
– Рассмотрены силы упругости и виды деформации тела.
– Сформулирован закон Гука.
– Рассмотрены главные отличия силы веса от силы тяжести.