что значит выражение обратимая операция какие известные вам логические операции обратимы
Обратимые вычисления
Термин компьютерная обратимость или обратимые вычисления относится к архитектуре компьютеров, которая является (по крайней мере приблизительно) обратимой, так что исходное состояние также может быть восстановлено из конечного результата во время вычислений.
Оглавление
Граница Неймана-Ландауэра
Современная компьютерная архитектура основана на необратимой логике. Это означает, что информация теряется при выполнении логических операций. Например, простое И имеет два входных сигнала, но только один выходной сигнал. Таким образом, один бит теряется, а количество возможных логических состояний сокращается с 4 до 2.
Обратимые логические процессы
Логические операции не обязательно должны быть необратимыми. Обратимые логические операции можно определить, и, как показал Ландауэр, логически обратимые процессы всегда физически обратимы (принцип Ландауэра).
В частности, можно показать, что все логические операции могут быть представлены как комбинация обратимых операций. Теоретически компьютер также можно построить с обратимой логикой. Кроме того, существует множество публикаций некоторых известных авторов, в которых рассматриваются концепции и механизмы по этой теме. Тем не менее, обратимые вычисления по сей день используются только в исследовательских целях.
недостаток
Поскольку информация должна сохраняться с помощью обратимой логики, в результате вычислений возникает большое количество дополнительных битов, которые необходимо сохранить.
Что значит выражение обратимая операция какие известные вам логические операции обратимы
Ещё давно, в 60-е годы как минимум, было замечено, что логические операции, лежащие в основе работы компьютеров, с физической точки зрения являются необратимыми процессами, т. е. они неизбежно сопровождаются ростом энтропии, т. е. при выполнении этих операций неизбежно происходит рассеяние энергии. (Причём существует фундаментальный нижний предел для количества энергии, рассеиваемой за одну логическую операцию.) Эта необратимость заключается в том, что при выполнении некоторых операций происходит потеря информации. Например, операция “и”:
После выполнения этой операции прежнее значение переменной a в общем случае уже нельзя восстановить, т. е. информация теряется.
Примерно тогда же, в 60-е годы, и возникла идея обратимых вычислений: если в качестве элементарных логических операций допускать только обратимые операции, то в принципе можно проводить вычисления вообще без затраты энергии (или, с поправкой на неидеальность: можно проводить вычисления со сколь угодно малыми затратами энергии). Обратимые логические операции действительно существуют. Например, “не” (a:=not a;), “исключающее или” (a:=a xor b;). Есть даже универсальные обратимые логические операции, например, “гейт Тоффоли”:
любое сколь угодно сложное обратимое вычисление можно представить в виде цепочки гейтов Тоффоли. Конечно, идея обратимых вычислений наталкивается на некоторые специфические трудности: например, в процессе вычисления происходит накопление “мусора”, который нельзя стереть. Но с этими трудностями можно успешно бороться.
До сих пор я тут излагал давно известные, общепризнанные истины. Теперь вот что: если обратимые вычисления в принципе не требуют затрат энергии, то они в принципе не должны требовать и затрат времени! То есть должен существовать способ выполнить сколь угодно длинную цепочку обратимых вычислений (содержащую, к примеру, 10 1000 элементарных операций) мгновенно (ну или, скажем, за сколь угодно короткий отрезок времени). Это следует из того, что обратимая логическая операция, в отличие от необратимой, не есть физический процесс, происходящий в пространстве и во времени.
«Иная» логика и обратимые вычисления
Начал вспоминать другие примеры создания «языков чужаков». Например, язык Клингонов из «Звёздного пути» тоже основан на латинице, но при этом достаточно проработан, имеет свой синтаксис и словарь. Языки народов Средиземья из «Властелина колец» – вообще отдельная история.
А ещё существуют такие языки, как Линкос, специально разработанный Гансом Фройденталем для межпланетного общения и основанный на предположении, что математика является универсальным языком общения для любых разумных существ.
В «Плоском мире» Терри Пратчетта тоже достаточно языков, но вроде это просто переименованные земные языки. А в отношении математики, как универсального языка, более уместно упомянуть английского биолога Джека Коэна, его соавтора по книге «Наука плоского мира», который на одной конференции затронул достаточно неожиданную тему: «Почему вы думаете, что пришельцы поймут вашу математику? А вдруг у них совершенно другой способ мышления?»
Эту цитату я прочитал у Джеймса Нэйшина, другого участника конференции, профессора университета на Гавайях, где она и проходила. На его сайте можно найти тексты двух выступлений, в какой-то мере спровоцированных данным вопросом: «Как пришельцы делают математику» и «Логика иных планет». Может это и выглядит не очень серьёзно, особенно когда разные виды логики приписаны жителями разных планет нашей солнечной системы. Однако, вот искал возможные ссылки на одну функцию, используемую для создания обратимых вентилей, и с удивлением обнаружил её у него в разделе, посвящённом логике жителей Юпитера.
Камень, ножницы, бумага
Что же особенного в «юпитерианской логике» и как она связана с обратимыми вычислениями? Нэйшин для её описания использует набор из трёх элементов, обозначаемых символами R,P,S, которые соответствуют первым буквам английских слов для камня, ножниц и бумаги. Игра «камень, ножницы, бумага» (о ней тут тоже писали и не раз) известна и на Гавайях как «дзян-кэн». По правилам игры один из трёх предметов побеждает другой исходя из циклического набора предпочтений. Это обычно изображается на круговой диаграмме, но можно записать и в строчку:
S обычной логики. Так что, задание отношений между элементами определяет аналоги логических операций. Правда, при циклическом наборе предпочтений между трёмя элементами некоторыми свойствами приходится пожертвовать. Что поделать, иная логика.
Таблица для аналога «ИЛИ» при таком подходе выглядит как
| Иное ИЛИ | R | P | S |
| R | R | P | R |
| P | P | P | S |
| S | R | S | S |
Таблица для операции «И» стоится аналогично
| Иное И | R | P | S |
| R | R | R | S |
| P | R | P | P |
| S | S | P | S |
Обратимые вычисления
А что с обратимыми вычислениями? О них уже тут тоже писали как, впрочем, и о троичной логике (тут, на geektimes, ещё тут) и даже вместе их пытались свести.
Обратимые вентили могут быть полезными для решения проблемы тепловыделения в процессорах следующих поколений, они тесно связаны с теорией квантовых вычислений. Да и тема сама по себе достаточно интересная. Об этом можно много где почитать, включая приведённые выше ссылки, так что постараюсь не особо распространяться на тему уже достаточно известных вещей.
Если совсем коротко, то вентиль обратим, когда значения на входах всегда можно восстановить по значениям на выходах. Для работы с двоичными данными обычно используют универсальные вентили Тоффоли или Фредкина. Оба вентиля имеют по три входа и три выхода, так как, в отличие от необратимого случая, из обратимых двоичных вентилей с двумя входами нельзя создать набор для выполнения произвольной операции над данными.
Попробуем представить обратимый аналог обычного вентиля «ИЛИ». Предположим, что у него два входа (и два выхода, раз уж он должен быть обратимым), на входы подаются двоичные значения, а один из выходов должен выдать результат операции «ИЛИ». Получается, что одно и то же значение 1 (ИСТИНА) на этом выходе может получиться при трёх разных комбинациях на входе: 11, 01, 10. Если бы второй выход мог иметь три разных значения, это можно было бы использовать для обращения такого вентиля.
Так что, уже достаточно простые оценки приводят к идее использовать троичную систему хотя бы на одном выходе. А что если попробовать работать с тремя значения на всех входах и выходах – можно ли получить обратимый вентиль, если использовать троичную логику?
Достаточно распространённой является троичная логика Лукасевича. Она может быть построена и уже упомянутым выше трюком с максимум и минимумом, если предположить, что третьему значению соответствует какое-нибудь число x, 0 00 01 0x 10 11 1x x0 x1 xx
и так как вентиль обратим, то и на выходе каждая из этих девяти пар должна появиться при одной из комбинаций на входе. Видно, что в этих парах любое значение первого (и второго) элемента встретится по три раза.
То есть, три нуля, три единицы, три икса. А вместо этого в таблице для троичного «ИЛИ» стоит только один ноль и пять единиц. Во второй таблице для «И» наоборот, пять нулей и одна единица, что тоже не подходит.
Поэтому, хотя обратимые троичные вентили по отдельности и троичная логика по отдельности достаточно широко используются, вместе их трудно свести. Тут и приходит на помощь «инопланетная» логика. Для наглядности заменим R,P,S на 0,1,$.
Так что, семикратное применение вентиля оставит любую пару значений без изменений, а обратная операция соответствует применению шести вентилей подряд. С вентилями Тоффоли и Фредкина проще, каждый из них совпадает со своим обратным.
Если подавать на вход только значения ноль и единица, то этот троичный вентиль реализует обычную логическую операцию «ИЛИ». Установив единицу на второй вход можно использовать второй выход как операцию «НЕ» от первого входа. Помимо этого, вентиль реализует операцию «разветвления» двоичного значения поданного на второй вход, если на первый подать ноль. Так что этот обратимый троичный вентиль является универсальным для работы с двоичными данными.
Он тоже универсален для двоичных операций, но в отличие от «ИЛИ», одного такого вентиля не достаточно для «разветвления». Правда, выбор операции на втором выходе был достаточно произволен. Операция же на первом входе однозначно определяются выбором трёх условий: (1) выполнять нужную логическую операцию для двоичных данных, (2) соответсвовать одному из значений на входе, (3) не зависеть от их перестановки.
Выбор второй операции тоже достаточно естественен и может быть использован для других моделей. Предположим, надо построить обратимый вентиль для логики Лукасевича. Проблема с этим уже была описана, некоторые значения появляются в таблице 3×3 пять раз, а их должно быть поровну, чтобы сделать обратимый вентиль.
Ещё ящерица и Спок
Можно продолжать и дальше; для построения похожих круговых диаграмм, особенно хорошо подходят наборы, в которых количество элементов равно простому числу.
Коллективная логика и «невозможные стрелки»
Надо сказать, что циклическая логика не такая уж «инопланетная». Один из наиболее характерных примеров связан с парадоксами Кондорсе и Эрроу относящимися к проблеме выбора. Типичное описание «парадокса голосования» можно найти в книге лауреата Нобелевской премии по экономике Кеннета Эрроу «Коллективный выбор и индивидуальные ценности».
Рассмотрим выбор из трёх альтернатив (например, выборы с тремя кандидатами) A, B, C. При этом, каждый голосующий имеет некую упорядоченную систему предпочтений. То есть, если первая альтернатива предпочтительнее второй, а вторая предпочтительная третьей, то первая тоже предпочтительнее третьей. Пример проблем с выбором, возникающий при нарушении этого критерия, тоже описан далее.
Такие упорядоченные предпочтения являются примером транзитивных отношений, а операции с аналогичным свойством ассоциативны, то есть, не зависят от расстановки скобок. Обсуждаемое ранее определение операции «ИЛИ» через задание отношений элементов хорошо согласуется с идеей выбора: операция «А ИЛИ В» – просто выбор между A и B, исходя из некого набора предпочтений (включая случай «А ИЛИ A», который, хотя и затруднительно назвать «выбором», тоже имеет вполне определённый результат, A).
Пусть кто-то полагает, что B лучше A, C лучше В (и по приведённому ранее критерию, C лучше A). Запишем этот выбор как
(1) A ((A || B) || C) = B || C = C,
(A || (B || C)) = A || C = A
Урок 15
§10. Другие логические операции
Содержание урока
Исключающее ИЛИ
Исключающее ИЛИ
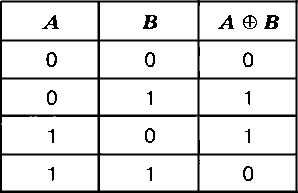
Функция, которую вы исследовали в последнем задании, называется исключающее ИЛИ. Её результат равен 1, если значения входных сигналов не равны (рис. 2.15).
Исключающее ИЛИ обозначается знаком ⊕. Смысл этой операции хорошо передаёт поговорка «либо пан, либо пропал»: возможен только один вариант из двух, но не оба одновременно.
Сравните таблицы истинности обычной операции «ИЛИ» и «исключающего ИЛИ».
Сравните таблицы истинности логических функций А ⊕ В и А ↔ В. Какая формула связывает две эти операции?
Операция исключающее ИЛИ иначе называется разделительной дизъюнкцией (это значит «один или другой, но не оба вместе») или сложением по модулю два. Второе название связано с тем, что её результат равен остатку от деления арифметической суммы А + В на 2:
Здесь mod обозначает операцию взятия остатка от деления.
Составьте таблицы истинности логических функций А ⊕ 0, А ⊕ 1 и А ⊕ А. Сравните значения каждой функции со столбцом А. Как можно упростить эти формулы?
Сравните таблицу истинности логической функции А • B + А • В (см. задание выше) с таблицей истинности операции исключающее ИЛИ. Какую формулу вы только что доказали?
Постройте таблицу истинности логической функции (А + В) • ( А + B ). Сравните её с таблицами истинности известных вам функций с двумя переменными. Какую формулу вы только что доказали?
Составьте таблицу истинности логической функции (А ⊕ В) ⊕ В. Сравните столбец значений функции со столбцом А. Какую формулу можно записать в результате сравнения?
Из результатов выполнения последнего задания следует важный вывод: если два раза применить к значению А операцию исключающее ИЛИ с одним и тем же значением В, то мы восстановим исходное значение А. В этом смысле исключающее ИЛИ — обратимая операция.
Какие ещё обратимые логические операции вы знаете?
Используя дополнительные источники, выясните, в каких языках программирования есть логическая операция «исключающее ИЛИ» и как она обозначается.
Запишите в тетради формулы, с помощью которых можно представить операции импликацию, эквиваленцию и исключающее ИЛИ через базовые логические операции: НЕ, И и ИЛИ.
Используйте результаты выполнения заданий в рабочей тетради.
Следующая страница 
Cкачать материалы урока
Учитель информатики
Сайт учителя информатики. Технологические карты уроков, Подготовка к ОГЭ и ЕГЭ, полезный материал и многое другое.
Логические выражения.
Информатика. Учебник для 9 класса (по учебнику К. Ю. Полякова, Е.А. Еремина, базовый уровень)
§11. Логические выражения.
Формализация
Ключевые слова:
Обозначив простые высказывания буквами — логическими переменными и используя логические операции, можно записать любое высказывание в виде логического выражения.
Логическое выражение — это выражение, результат вычисления которого — логическое значение (истина или ложь).
Например, пусть система сигнализации должна дать аварийный сигнал, если вышли из строя два из трёх двигателей самолёта. Обозначим высказывания:
А = Первый двигатель вышел из строя;
В = Второй двигатель вышел из строя;
С = Третий двигатель вышел из строя;
X = Аварийная ситуация.
Тогда логическое высказывание X можно записать в виде логического выражения (логической формулы):
X = (А и В) или (А и С) или (В и С).
Это выражение может быть записано с помощью других обозначений:
X = (А • В) + (А • С) + (В • С). (*)
Таким образом, мы выполнили формализацию.
Формализация — это переход от конкретного содержания высказываний к записи с помощью формального языка.
При вычислении логических выражений установлен такой порядок выполнения операций:
1) действия в скобках;
2) отрицание (НЕ);
3) логическое умножение (И), слева направо;
4) логическое сложение (ИЛИ), слева направо.
Можно ли убрать скобки в выражении (*)? Почему?
Уберите лишние скобки в логических выражениях:
а) X = (А + (В • С) • (А + С));
б) X = (А + B) • (C • А) • (А + (B + C))).
Вычислите значение логического выражения X = (А • В + С) • (А + C) при:
а) А = О, В = О, С = 1;
б) А = О, В = 1, С = 1;
в) А = 1, В = 1, С = 0.
Таблицы истинности
Любую логическую функцию можно задать с помощью таблицы истинности, которая показывает, чему равно значение логического выражения при всех возможных комбинациях значений исходных переменных. Построим таблицу истинности для выражения
X = А и не В или не А и B,
которое можно также записать в виде
Сколько строк в таблице истинности выражения с двумя переменными?
Будем вычислять выражение по частям: добавим в таблицу истинности дополнительные столбцы А • B и А • В, а потом выполним операцию ИЛИ с этими значениями (рис. 2.18).
Рис. 2.18
Из этой таблицы истинности видно, что при некоторых значениях переменных значение X истинно, а при некоторых — ложно. Такие выражения называют вычислимыми.
Высказывание «Вася — школьник или он не учится в школе» всегда истинно (для любого Васи). Выражение, истинное при любых значениях переменных, называется тождественно истинным или тавтологией.
Высказывание «Сегодня безветрие, и дует сильный ветер» никогда не может быть истинным. Соответствующее логическое выражение всегда ложно, оно называется тождественно ложным или противоречием.
Выполните формализацию высказываний, о которых шла речь в последних двух абзацах. Запишите формулы для упрощения каждого из них.
Постройте самостоятельна таблицу истинности логического выражения X = (А + В) • (A + B). Сравните её с таблицей на рис. 2.18. Истинно ли высказывание «Разные логические выражения могут определять одну и ту же логическую функцию»?
Если два выражения принимают одинаковые значения при всех значениях переменных, они называются равносильными или тождественно равными. Равносильные выражения определяют одну и ту же логическую функцию, т. е. при одинаковых исходных данных приводят к одинаковым результатам.
Сколько строк в таблице истинности выражения с тремя переменными?
Постройте таблицу истинности логического выражения
Х = А • В + А • С + В • С.
Предположим, что нам известна только часть таблицы истинности для функции трёх переменных (рис. 2.19).
Рис. 2.19
Как вы думаете, можно ли по такой части таблицы истинности определить логическую функцию? Почему?
Всего в таблице истинности функции от трёх переменных 2 3 = 8 строк, для каждой из них нужно знать, чему равно значение функции. В нашем примере пять значений функции неизвестны, причём каждое из них может быть равно 0 или 1, т. е. у нас есть 5 свободных бит.
Сколько различных значений можно закодировать с помощью 5 бит?
Как вы нашли это значение?
Итак, таблице на рис. 2.19 могут соответствовать 32 различные логические функции. Проверим, подходят ли следующие варианты:
Прежде всего, заметим, что в столбце значений функции два нуля и одна единица. Следовательно, вариант а) не подходит, потому что цепочка операций ИЛИ со всеми переменными (или их инверсиями, обратными значениями) даст только один ноль — в случае, когда все слагаемые равны нулю.
Проверяем вариант б), подставляя значения переменных А, В и С сначала из первой строки таблицы, потом из второй и третьей. В первой строке получаем A • С + В = 1 • 1 + 0 = 1, этот результат совпадает со значением функции в этой строке. Для второй строки A • С + В = 1 • 1 + 1 = 1, значит, эта функция тоже не подходит.
Проверьте самостоятельно, подходят ли остальные варианты.
Скажите без вычислений, сколько нулей и сколько единиц должно быть в последнем столбце таблицы истинности функций с тремя переменными:
Теперь предположим, что нам известна часть таблицы какой-то логической функции, причём с пропусками (рис. 2.20).
Рис. 2.20
Выясним, какие из следующих функций могут соответствовать этой таблице:
Во-первых, обратим внимание, что в столбце значений функции две единицы, поэтому сразу делаем вывод, что это не могут быть цепочки двух операций И (ответы б) и г) неверные). Остались три цепочки из операций ИЛИ, причём для верхней строки (при А = 0 и С = 1) мы должны получить 0 при каком-то выборе неизвестного значения В. Подставляем А = 0 и С = 1 в формулы-кандидаты:
Видим, что в случае а) сумма не может быть равна нулю, это неверный ответ. А варианты в) и д) подходят: в первом из них нужно в первой строке поставить в пустую ячейку 1, а во втором — 0.
Кратко решение можно записать так:
1) поскольку в столбце значений функции один ноль, это не может быть цепочка операций И; остаются только цепочки операций ИЛИ;
2) для того чтобы получить нулевое значение функции в первой строке таблицы, нужно, чтобы переменная А (равная 0 в этой строке) входила в логическую сумму без инверсии (к ней не должна применяться операция НЕ) а переменная С (равная 1) — с инверсией;
3) этим условиям удовлетворяют функции в) и д).
Известна часть таблицы какой-то логической функции с пропусками (рис. 2.21).
Рис. 2.21
Выясните, какие из следующих функций могут соответствовать этой таблице:
Составление условий
Логические выражения часто используются при решении математических задач с помощью компьютеров.
Построим условия (логические выражения), соответствующие заштрихованным областям на числовой оси (рис. 2.22).
Рис. 2.22
На рисунке 2.22, а выделен отрезок [3; 6]. Для того чтобы определить такую область, нужно ограничить значение х с двух сторон: оно должно быть больше или равно трём и меньше или равно шести, причем эти два условия должны выполняться одновременно, т. е. их нужно связать с помощью операции И:
Область на рис. 2.22, б — это объединение двух отрезков. Мы можем отдельно записать условия для каждого отрезка и связать их с помощью операции ИЛИ:
(1 ≤ х) и (х ≤ 3) или (5 ≤ х) и (х ≤ 8).
Запишите условие, которое определяет область на рис. 2.22, в.
Теперь рассмотрим задачу с областью на плоскости. Запишем условие, соответствующее заштрихованной части (рис. 2.23).
Рис. 2.23
Требуется составить логическое выражение, зависящее от переменных х и у, которое будет равно 1 (истинно) внутри заштрихованной области и равно 0 вне её.
Рис. 2.24
Запишите условие, которое определяет области на рисунках (рис. 2.25).
Рис. 2.25
Построим логическое выражение для области на рис. 2.26.
Рис. 2.26
Можно разделить заштрихованную область на две части (рис. 2.27).
Рис. 2.27Обе области находятся внутри круга радиуса 1 с центром в начале координат, т. е. в области х 2 + у 2 ≤ 1. Первая область описывается выражением
(х 2 + у 2 ≤ 1) и (х ≤ 0),
а вторая — выражением
Поскольку нам нужно «сложить» две области, эти выражения нужно объединить с помощью операции логического сложения (ИЛИ):
Общее условие х 2 + у 2 ≤ 1 можно вынести за скобки:
Попробуйте ещё упростить полученное условие.
Запишите условие, которое определяет области на рисунках (рис. 2.28).
Рис. 2.28
Логические схемы
Вернёмся снова к примеру с системой аварийной сигнализации самолёта. Предположим, что на каждом двигателе установлен логический датчик, который выдаёт условный сигнал 1 (например, высокий уровень напряжения), если двигатель неисправен, и условный сигнал 0, если двигатель исправен. Требуется построить логическую схему — схему логического устройства, — которая при аварии выдаёт условный сигнал 1, а в режиме нормальной работы — сигнал 0.
Сигналы от трёх двигателей назовём А, Б и С. В начале параграфа мы уже составили логическое выражение для запуска аварийной сигнализации:
Х = А • В + А • С + В • С.
Здесь три логических умножения и два логических сложения. Сначала выполняются все операции умножения (слева направо), а затем — все операции сложения (тоже слева направо). Расставим номера операций:
| 1 | 4 | 2 | 5 | 3 | ||||||||
| Х | = | А | • | В | + | А | • | С | + | В | • | С. |
Последней выполняется вторая операция сложения. Поэтому последний элемент в схеме — это элемент логического сложения ИЛИ (рис. 2.29).
Рис. 2.29
На первый вход этого элемента ИЛИ подаётся сигнал А • В + А • С, в этом выражении последняя операция — логическое сложение, добавляем ещё один элемент ИЛИ (рис. 2.30).
Рис. 2.30
Три операции логического умножения добавляют в схему три элемента И (рис. 2.31).
Рис. 2.31
Запишите в тетради логическое выражение по логической схеме (рис. 2.32).
Рис. 2.32
Постройте логическую схему, соответствующую выражению:
в) Z = A • B + A • B • C.
Работа в парах. Один из вас пусть нарисует логическую схему для выражения X = A + В • С (черта сверху обозначает, что операция отрицания применяется ко всему выражению), а второй — для выражения Y = (А + В) (А + С). Постройте таблицы истинности для своих выражений и сравните их. Какую формулу вы сейчас вместе доказали?
Работа в парах. Запишите логическое выражение, включающее 5-6 операций, и предложите соседу нарисовать логическую схему. Проверьте и обсудите с ним его решение.
Путешествуя по Зазеркалью, Алиса увидела дверь с тремя кнопками, которые были отмечены буквами А, В и С. На двери висела схема (рис. 2.33).
Рис. 2.33
На какую (одну!) из трёх кнопок нужно нажать Алисе, чтобы открыть дверь?
Выводы
• Формализация — это переход от конкретного содержания высказываний к записи с помощью формального языка.
• В логических выражениях операции выполняются в следующем порядке:
1) действия в скобках;
2) отрицание (НЕ);
3) логическое умножение (И), слева направо;
4) логическое сложение (ИЛИ), слева направо.
Для изменения порядка действий используются скобки.
• Таблица истинности логического выражения показывает, чему равно значение выражения при всех возможных комбинациях значений исходных переменных.
• Логические выражения, истинность которых зависит от значений исходных переменных, называют вычислимыми.
• Логическое выражение, которое всегда истинно, называется тождественно истинным или тавтологией. Выражение, которое всегда ложно, называют тождественно ложным или противоречием. Пример тождественно истинного выражения: А + А, пример тождественно ложного: А • А.
• Два выражения, принимающие одинаковые значения при всех значениях переменных, называются равносильными или тождественно равными. Равносильные выражения определяют одну и ту же логическую функцию.
Нарисуйте в тетради интеллект-карту этого параграфа.
Вопросы и задания
1. Что можно сделать для того, чтобы изменить порядок выполнения действий в логических выражениях?
2. Поясните разницу между терминами «логическое выражение» и «логическая функция».
3. Как можно доказать (или опровергнуть) логическую формулу?
4. Можно ли сказать, что таблица истинности однозначно определяет:
а) логическое выражение;
б) логическую функцию?
5. Что такое вычислимое логическое выражение?
6. Что такое равносильные выражения?
7. Выполните по указанию учителя задания в рабочей тетради.