Ии решил что это математика
Математики придумали задачу, которую искусственный интеллект не способен решить принципиально
Международная группа исследователей систем машинного обучения и искусственного интеллекта пришла к неутешительному выводу – они более ограничены, чем мы полагали. Это проистекает из математической природы их архитектуры и методов работы. Согласно «Теореме о неполноте» Геделя и положениям его же Второй теоремы, в реальности далеко не все математические задачи решаемы. А так как машинное обучение имеет именно математическую природу, то у него есть свой предел.
Одной из насущных проблем в машинном обучении является «оценка максимума». Ее можно проиллюстрировать на таком примере: есть некий сайт, который посетит неизвестное количество пользователей, чьи интересы заранее тоже неизвестны, но в целом набор параметров конечен. Нужно создать такой алгоритм, который обеспечит им всем показ целевой рекламы с точностью, близкой к абсолютной. При моделировании подобной ситуации ученые вышли на однозначное сходство с условиями «Гипотезы континуума», которая долго время находилась в списке нерешенных задач математики.
Если говорить точнее, то и для Теоремы о неполноте, и для Гипотезы континуума, не существует ответа в привычном для машины виде. ИИ, даже самый продвинутый, при решении подобной задачи выйдет на такой шаг, когда не сможет дать оценку «верно» или «неверно». Человек бы просто махнул рукой, ввел бы некоторое дополнительное условие или проигнорировал важность выбора, принял решение интуитивно. Алгоритмы машинного обучения не позволяют такой вольности, поэтому ИИ не сможет продолжить работу.
Бремя недоказуемости, увы, свойственно слишком многим математическим задачам, а потому вероятность того, что ИИ рано или поздно столкнется с похожей ситуацией, приближается к 100 %. Значит, нам нужно уже сегодня придумать, как позволить ему обойти подобные парадоксы. Но при этом сохранить ту точность анализа ситуации и принятия решений, ради которой мы и стараемся обучать наш рукотворный разум. А это тем сложнее, чем большее отклонение от правил допускается в его работе.
Кабинет Информатики
«Искусственный интеллект в образовании»
9-11 класс
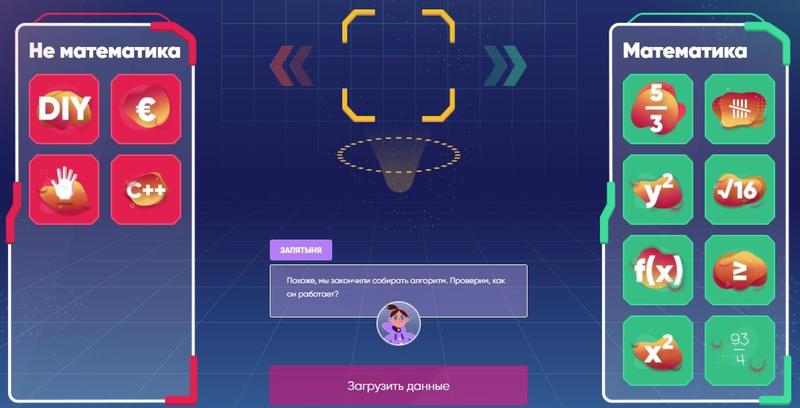
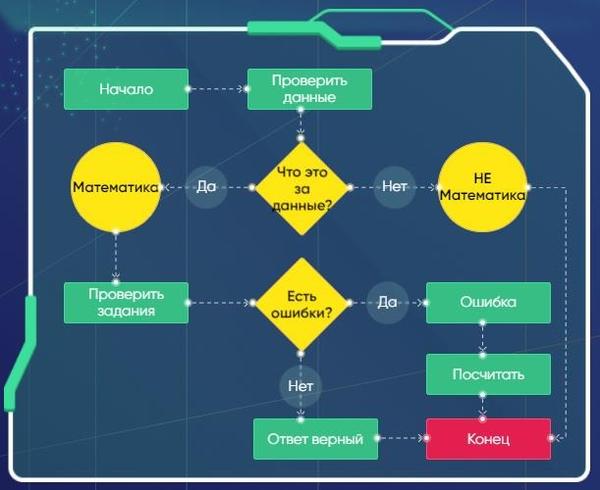
Шаг 1. Этап 1. Учим ИИ узнавать цифры и распознавать, что относится к математике, а что нет
Как и человеку, искусственному интеллекту необходимы данные для обучения.
Представьте, как ребенок учит буквы: он часто видит их в книжках и вывесках, рассматривает азбуку или кубики, и каждый раз ему говорят, что за букву он видит. После многократных повторений ребенок постепенно запоминает значение символов. Примерно так же обучают искусственный интеллект для того, чтобы он научился узнавать какие-то символы, например, цифры.
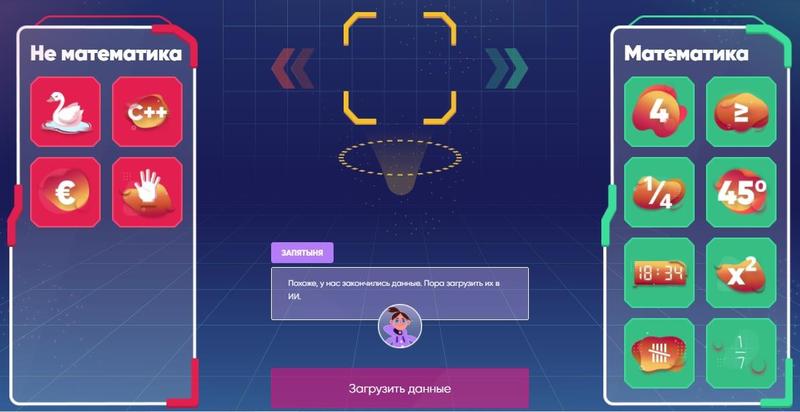
Задача ученика: много раз показать ИИ математические символы (цифры, знаки, выражения и т.д.) и научить ИИ отличать их от всех прочих.
ИИ распознает, что относится к математике, а что нет
В данной задаче, как и в жизни, нет единственно правильного решения, т.к. некоторые символы могут относиться и не относиться к математике. Например, время на электронных часах или градусы.
Шаг 1. Этап 2. Проверка
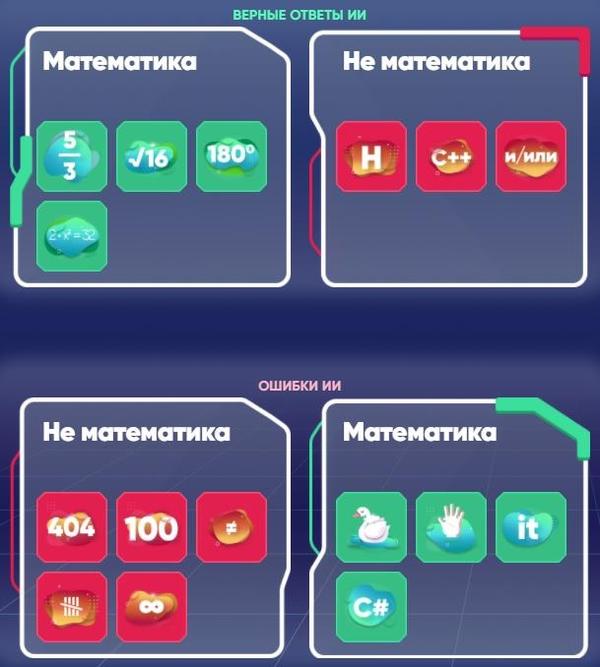
Иногда искусственный интеллект не может научиться с первого раза и ошибается. Для того, чтобы найти ошибки, указать на них и помочь искусственному интеллекту обучиться лучше, нужна человеческая помощь. Во время обучения искусственного интеллекта алгоритму недостаточно только исходных данных, которые он получает от человека. Во время работы может потребоваться их корректировка. Это означает, что человек должен проанализировать промежуточные результаты работы алгоритма и сообщить, в каких случаях он отработал верно, а в каких нет. Таким образом, алгоритм подстроится под решение задачи более точно.
Задача ученика: посмотреть на первые результаты работы искусственного интеллекта и сделать такую корректировку.
ИИ распознает, что относится к математике, а что нет
Шаг 2. Этап 1. Загрузка правил
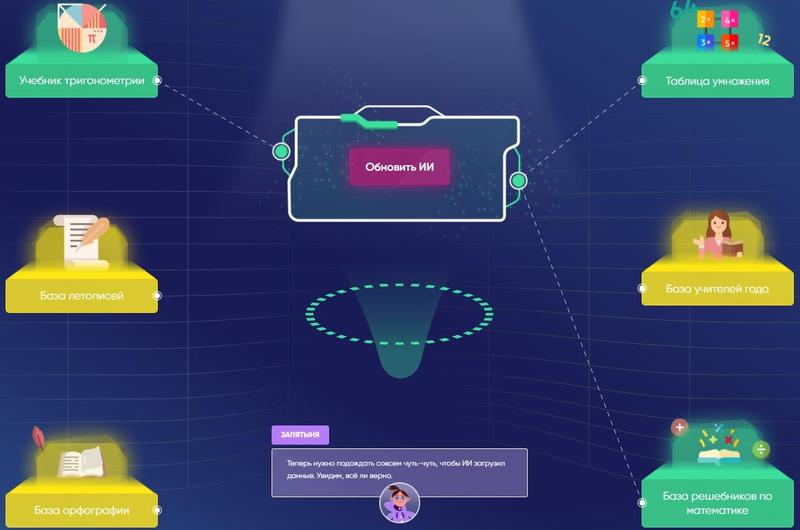
Кроме распознавания каждого отдельного символа, необходимо уметь собирать все прочитанные символы в осмысленную запись. Для этого алгоритм должен знать, по каким именно правилам строится математическая запись. Эти правила должны быть заложены в алгоритм; только тогда он сможет проверять правильность прочитанных выражений.
Задача ученика: подключить ИИ к базам данных, где собраны правила математики.
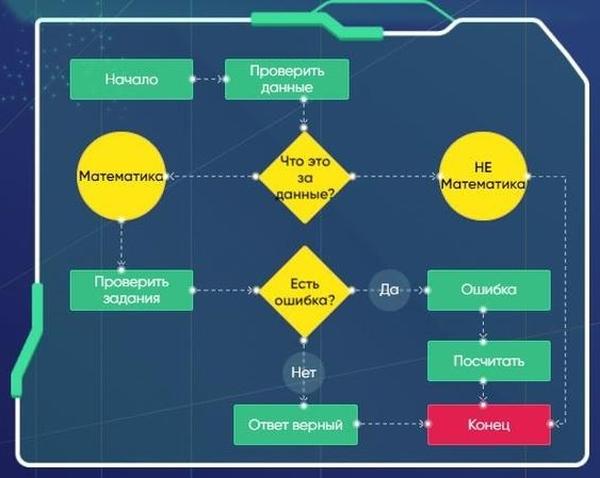
Шаг 2. Этап 2. Нахождение и подсчет ошибок
После того, как машина научится проверять разные математические выражения на ошибки, нам необходимо сообщить ей, что делать с этой информацией дальше. Мы должны загрузить в нашу программу конкретные инструкции о том, как поступать при обнаружении ошибки. Программа должна не просто фиксировать ошибки, но и вести их учет: подсчитывать, сколько раз ошибся ученик при выполнении задания.
Задача ученика: написать алгоритм, который научит ИИ находить ошибки с помощью правил математики и считать количество сделанных ошибок.
Шаг 3. Этап 1. Подготовка выводов
Шаг 3. Этап 2. Составление индивидуальных заданий
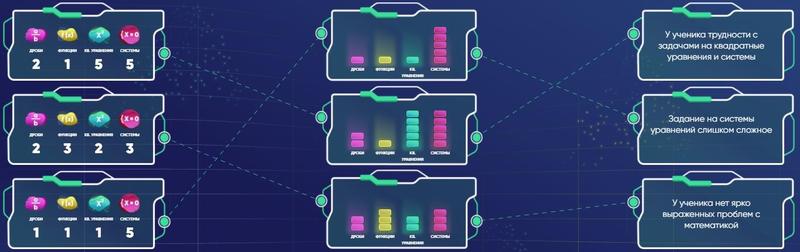
При наличии большого количества данных о результатах выполнения разных работ ученика, программа может предсказать, какие именно задания будут для него в будущем самыми полезными, ведь она «помнит» и «знает», какие именно типы заданий вызвали у него в прошлом больше всего проблем. Даже по результатам одной работы можно сделать вывод о том, в каких именно заданиях ученик сделал больше всего ошибок, а с какими он справляется хорошо. Если результаты ученика высокие, программа может подобрать для него более сложные упражнения, а если ошибок много, то сложность упражнений на данное правило повышать не следует, лучше дать задания попроще.
Задача ученика: подготовить для ИИ алгоритм выбора сложности заданий. Это необходимо для составления персонального теста ученику на основе выводов ИИ по каждой из его работ.
ИИ поможет ученым совершить открытия в математике, решив задачи 40-летней давности
Перед алгоритмами машинного обучения стоит важная задача: обнаружить математические закономерности, которые ни одному ученому не удавалось найти.
Группа исследователей из Сиднейского университета (Австралия) и Оксфордского университета (Великобритания) использовала системы искусственного интеллекта, разработанные компанией DeepMind, чтобы продемонстрировать на что способны алгоритмы машинного обучения. Об этом сообщает издание sciencealert.com.
Читайте лучшие материалы раздела на странице “Фокус. Диджитал” в Facebook
“Математические задачи считаются одними из самых сложных в интеллектуальном плане”, — говорит ученый Джорди Уильямсон из Сиднейского университета. “Хотя математики и раньше использовали машинное обучение (МО), чтобы упростить анализ сложных наборов данных, мы впервые использовали компьютеры для выдвижения гипотез”.
В частности, ИИ пытается решить математическую задачу, связанную с симметрией многомерной алгебры, которая оставалась нерешенной в течение 40-ка лет (т.н. многочлен Каждана-Люстига).
В ходе исследования ученые задействовали модель контролируемого обучения (метод машинного обучения, — ред.), при помощи которой смогли обнаружить ранее неизвестную взаимосвязь между двумя разными типами математических узлов, что привело к выдвижению совершенно новой теоремы.
“Теория узлов используется не только в математике, но и в других сложных областях науки, включая генетику, гидродинамику, в исследованиях поведения короны Солнца. Таким образом, открытия, которые делает ИИ, могут повлиять на развитие и этих сфер знаний”, — пишет СМИ.
“Руководствуясь математической интуицией, алгоритмы МО обеспечили мощную основу, опираясь на которую, мы сможем выявлять интересные и доказуемые гипотезы в областях, где необходима обработка большого объема данных или там, где объекты слишком велики для изучения с помощью классических методов”, — прокомментировал математик Андраш Юхас из Оксфордского университета.
Исследование показывает, что высокоскоростная, сверхнадежная и крупномасштабная обработка данных может стать дополнительным инструментом, работающим в паре с естественной интуицией математиков. “Когда вы имеете дело со сложными и длинными уравнениями, это может иметь большое значение”, — отмечает СМИ.
Исследователи надеются, что их работа приведет к дальнейшему развитию партнерства между учеными в области математики и ИИ, благодаря чему они совершат множество открытий, которые в противном случае остались бы незамеченными. А все потому что алгоритмы МО способны прорабатывать сценарии, которые люди склонны пропускать, отбрасывать или попросту не замечать.
“ИИ — необычный инструмент”, — говорит Уильямсон. “Эта работа — одна из первых, когда она продемонстрировала свою полезность для истинных математиков, таких как я. Интуиция, безусловно, важна, но ИИ может помочь нам найти связи, которые человеческий разум не всегда может легко обнаружить”.
Кабинет Информатики
«Искусственный интеллект в образовании»
5-8 класс
Шаг 1. Этап 1. Учим ИИ узнавать цифры и распознавать, что относится к математике, а что нет
Как и человеку, искусственному интеллекту необходимы данные для обучения.
Представьте, как ребенок учит буквы: он часто видит их в книжках и вывесках, рассматривает азбуку или кубики, и каждый раз ему говорят, что за букву он видит. После многократных повторений ребенок постепенно запоминает значение символов. Примерно так же обучают искусственный интеллект для того, чтобы он научился узнавать какие-то символы, например, цифры.
Задача ученика: много раз показать ИИ математические символы (цифры, знаки, выражения и т.д.) и научить ИИ отличать их от всех прочих.
ИИ распознает, что относится к математике, а что нет
В данной задаче, как и в жизни, нет единственно правильного решения, т.к. некоторые символы могут относиться и не относиться к математике. Например, время на электронных часах или градусы.
Шаг 1. Этап 2. Проверка
Иногда искусственный интеллект не может научиться с первого раза и ошибается. Для того, чтобы найти ошибки, указать на них и помочь искусственному интеллекту обучиться лучше, нужна человеческая помощь. Во время обучения искусственного интеллекта алгоритму недостаточно только исходных данных, которые он получает от человека. Во время работы может потребоваться их корректировка. Это означает, что человек должен проанализировать промежуточные результаты работы алгоритма и сообщить, в каких случаях он отработал верно, а в каких нет. Таким образом, алгоритм подстроится под решение задачи более точно.
Задача ученика: посмотреть на первые результаты работы искусственного интеллекта и сделать такую корректировку.
ИИ распознает, что относится к математике, а что нет
Шаг 2. Этап 1. Загрузка правил
Кроме распознавания каждого отдельного символа, необходимо уметь собирать все прочитанные символы в осмысленную запись. Для этого алгоритм должен знать, по каким именно правилам строится математическая запись. Эти правила должны быть заложены в алгоритм; только тогда он сможет проверять правильность прочитанных выражений.
Задача ученика: подключить ИИ к базам данных, где собраны правила математики.
Шаг 2. Этап 2. Нахождение и подсчет ошибок
После того, как машина научится проверять разные математические выражения на ошибки, нам необходимо сообщить ей, что делать с этой информацией дальше. Мы должны загрузить в нашу программу конкретные инструкции о том, как поступать при обнаружении ошибки. Программа должна не просто фиксировать ошибки, но и вести их учет: подсчитывать, сколько раз ошибся ученик при выполнении задания.
Задача ученика: написать алгоритм, который научит ИИ находить ошибки с помощью правил математики и считать количество сделанных ошибок.
Шаг 3. Этап 1. Подготовка выводов
Шаг 3. Этап 2. Составление индивидуальных заданий
При наличии большого количества данных о результатах выполнения разных работ ученика, программа может предсказать, какие именно задания будут для него в будущем самыми полезными, ведь она «помнит» и «знает», какие именно типы заданий вызвали у него в прошлом больше всего проблем. Даже по результатам одной работы можно сделать вывод о том, в каких именно заданиях ученик сделал больше всего ошибок, а с какими он справляется хорошо. Если результаты ученика высокие, программа может подобрать для него более сложные упражнения, а если ошибок много, то сложность упражнений на данное правило повышать не следует, лучше дать задания попроще.
Задача ученика: подготовить для ИИ алгоритм выбора сложности заданий. Это необходимо для составления персонального теста ученику на основе выводов ИИ по каждой из его работ.
Символьная математика, наконец, начинает поддаваться нейросетям
Переведя на язык машин часть сложных математических уравнений, исследователи создали систему с искусственным интеллектом, надеясь, что она даст ответы на ещё более сложные вопросы

Переводя задачи символьной математики в древовидные структуры, мы, наконец, можем заставить нейросети решать абстрактные задачи
Более 70 лет назад исследователи на переднем крае изучения искусственного интеллекта (ИИ) придумали нейросети – революционный способ представить работу мозга человека. В мозге человека сети, состоящие из миллиардов связанных между собой нейронов, осмысливают приходящие с органов чувств данные, что позволяет нам учиться на опыте. Искусственные нейросети тоже умеют фильтровать через взаимосвязанные слои данные в огромных количествах, и, пользуясь самостоятельно выученными правилами, делать предсказания и распознавать закономерности.
Сегодня люди считают нейросети некоей панацеей из области ИИ, способной решать любые технические задачи, которые можно переформулировать в виде задач на распознавание закономерностей. Они умеют делать [почти] естественно звучащие переводы с языка на язык. Приложения для работы с фотографиями используют их для распознавания и разделения по категориям лиц, встречающихся на снимках. Программы на основе нейросетей обыграли лучших игроков мира в разные настольные игры, включая шахматы и го.
Однако в одной области нейросети традиционно отставали: в решении сложных задач символьной математики. Это, например, типичные задачи из курсов дифференциального и интегрального исчисления. Проблемы возникают по причине устройства самой математики, требующей точных решений задач. Нейросети тем временем обычно полагаются на вероятности. Они учатся распознавать закономерности – какой из вариантов перевода на испанский лучше звучит, или как выглядит ваше лицо на фото – и способны создавать новые.
Ситуация изменилась в конце прошлого года, когда Гийом Лампл [Guillaume Lample] и Франсуа Шартон [François Charton], пара специалистов по информатике из парижской исследовательской группы ИИ в Facebook, раскрыли первый удачный подход к решению задач символьной математики при помощи нейросетей. В их метод не входят обработка гор цифр или числовые аппроксимации. Вместо этого они сыграли на сильных сторонах нейросетей, переформулировав математические задачи в терминах задач, уже почти решённых: переводов с языка на язык.
«В институте мы оба изучали математику и статистику», — сказал Шартон, изучающий применение ИИ в математике. «Изначально мы говорили на языке математики».
В итоге программа Лампла и Шартона может выдавать точные решения сложных интегралов и дифференциальных уравнений – включая и такие, на которых спотыкаются популярные математические программы со встроенными правилами решения задач.

Франсуа Шартон (слева) и Гийом Лампл, специалисты по информатике из парижской исследовательской группы ИИ в Facebook
Новая программа эксплуатирует одно из основных достижений нейросетей: способность самостоятельно формулировать правила работы. В итоге, «правила и исключения не хранятся отдельно», — сказал Джей Маклиланд, психолог из Стэнфордского университета, использующий нейросети для моделирования процесса изучения математики людьми. На практике это означает, что программа не спотыкается на самых сложных интегралах. В теории такой подход может вывести нетрадиционные «правила», которые помогут человеку или машине разобраться с нерешёнными на сегодня задачами. Это могут быть такие математические задачи, как открытие новых доказательств или понимание природы самих нейросетей.
Конечно, пока такого мы не видим. Но команда явно утвердительно ответила на вопрос возрастом в несколько десятков лет – может ли ИИ заниматься символьной математикой? «Модели у них общепризнанные. Алгоритмы общепризнанные. Они хитрым образом формулируют задачи», — сказал Войцех Заремба, сооснователь группы исследования ИИ OpenAI.
«Им удалось создать нейросети, способные решать задачи, выходившие за рамки возможностей машин, следовавших правилам, — сказал Маклиланд. – И это очень здорово».
Обучаем компьютер математическому языку
Компьютеры всегда хорошо справлялись с обработкой чисел. Системы компьютерной алгебры комбинируют десятки и сотни чётко определённых алгоритмов, жёстко прописанных в коде. Обычно они строго следуют правилам, направленным на выполнение конкретных операций, и не приемлют исключений. Для многих символьных задач они выдают численные решения – с точностью, достаточной для инженерных и физических целей.
Нейросети так не работают. В них не записаны чёткие правила. Они обучаются на больших наборах данных – чем больше, тем лучше – и используют статистику, чтобы делать очень хорошее приближение. В процессе они обучаются тому, что даёт наилучший результат. Особенно хороши программы перевода текстов: они переводят не пословно, а сразу целыми фразами в контексте всего текста. Исследователи из Facebook решили, что это может стать не препятствием, а преимуществом при решении задач символьной математики. Такой подход даёт программе некую свободу в решении.
Такая свобода особенно полезна для определённых задач открытого типа, например, интегрирования. У математиков есть старая поговорка: «взятие производных – действие механическое, а интегралов – творческое». Чтобы найти производную функции, нужно следовать хорошо описанным действиям. Но при поиске интеграла часто требуется что-то ещё, что-то более близкое к интуиции, чем к вычислениям.
Группа из Facebook подозревала, что эту интуицию можно аппроксимировать при помощи распознавания образов. «Интегрирование – одна из наиболее похожих на распознавание закономерностей задач в математике», — сказал Шартон. Так что хотя нейросеть может и не понимать, что делают функции, или что означают переменные, она вырабатывает определённый инстинкт. Нейросеть начинает «чувствовать», что может сработать, даже не понимая, почему.
Чтобы дать нейросети возможность работать с символами, как это делают математики, Шартон и Лампл начали с перевода математических выражений в более удобную форму. В итоге они представили их в виде деревьев – в формате, похожем на разбор членов предложения в виде диаграммы. Математические операторы – сложение, вычитание, умножение, деление – стали узлами дерева, как и возведение в степень или тригонометрические функции. Аргументы (переменные и числа) стали его листьями. Древовидная структура, за некоторыми редкими исключениями, отражает то, как операции располагаются внутри длинных выражений.
«Изучая большую функцию, мы можем видеть, что она состоит из более мелких, и интуитивно представляем, каким может быть решение, — сказал Лампл. – Мы думаем, что модель пытается находить в символах подсказки по поводу решения». Он сказал, что этот процесс сравним с тем, как люди берут интегралы – и вообще решают математические задачи – сводя их к узнаваемым подзадачам, которые они уже решали ранее.
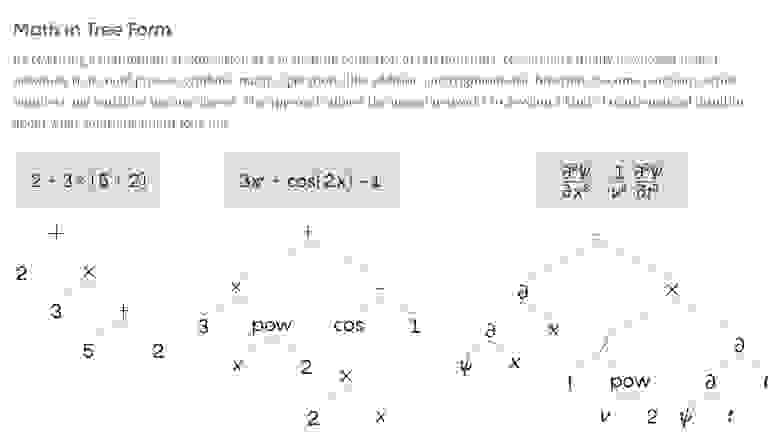
Переписав уравнения в виде ветвящихся наборов взаимосвязей, исследователи создали нейросети, способные работать с символьной математикой. Математические операторы – сложение, вычитание, умножение, деление – становятся узлами дерева, а аргументы (переменные и числа) — листьями. Такой подход позволяет нейросети вырабатывать что-то вроде математической интуиции.
Разработав такую архитектуру, исследователи использовали базу элементарных функций, чтобы сгенерировать несколько обучающих наборов данных, в сумме содержащих порядка 200 млн уравнений и их решений, представленных в виде деревьев. Затем они скормили эти данные нейросети, чтобы она обучилась тому, как выглядят решения этих задач.
После обучения настала пора посмотреть, на что способна нейросеть. Учёные испытали её на 5000 уравнений, уже без готовых ответов (ни одно из них, правда, нельзя было отнести к «нерешаемым»). Нейросеть отлично справилась с задачей, и нашла правильные решения для большинства из них. Особенно хорошо ей удавалось интегрирование, она решила почти 100% из таких испытательных задач, но немного хуже справилась с обычным дифференцированием.
На выдачу правильного решения почти всех задач у программы обычно уходило не более 1 секунды. На задачах по интегрированию она обогнала по скорости и точности популярные программы для решения задач, Mathematica и Matlab. Команда из Facebook сообщила, что нейросеть даже выдавала решения таких задач, которые были не под силу коммерческим программам.
Что в чёрном ящике
Несмотря на все эти результаты, математик Роджер Гермундсон, возглавляющий отдел исследования и разработки компании Wolfram, производителя пакета Mathematica, не согласен с таким прямым сравнением. Исследователи из Facebook сравнили свой метод только с небольшим количеством функций пакета Mathematica – integrate для интегралов и DSolve для дифференциальных уравнений. Однако у пользователей Mathematica есть доступ к сотням других инструментов.
Гермундсон также отметил, что, несмотря на огромный размер набора обучающих данных, в него входили только уравнения с одной переменной, и основанные на элементарных функциях. «Это тонкий срез всех возможных выражений», — сказал он. Нейросеть не проверяли на более запутанных функциях, которые часто используются в физике и финансах, типа функции ошибок или функции Бесселя (группа из Facebook ответила, что это будет возможно в будущих версиях нейросети, после небольших модификаций).
А Фредерик Гибу, математик из Калифорнийского университета в Санта-Барбаре, изучавший методы использования нейросети для решения дифференциальных уравнений в частных производных, не был убеждён в непогрешимости нейросети, созданной группой из Facebook. «Нужно быть уверенным, что система сработает во всех случаях, а не только на нескольких избранных задачах, — сказал он, — а здесь такой уверенности нет». Другие критики отмечали, что нейросеть группы из Facebook не понимает математику, а просто делает очень хорошие догадки.
И всё же они соглашаются с тем, что новый подход будет полезным. Гермундсон и Гибу считают, что нейросети заслужат себе место в ряду программ для решения уравнений следующего поколения – просто ряд будет очень длинным. «Думаю, что они станут одним из множества инструментов», — сказал Гермундсон.
Кроме решения конкретной задачи из символьной математики, работа группы из Facebook служит вдохновляющим доказательством работоспособности принципа и его возможностей. «Математиков в целом очень впечатлит, если эти технологии позволят им решить задачи, недоступные до этого людям», — сказал Андерс Хансен, математик из Кембриджского университета.
Ещё одно вероятное направление использования нейросетей, которое стоит изучить – разработка автоматических генераторов теорем. Математики всё чаще ищут способы использовать ИИ для генерации новых теорем и доказательств, хотя «лучшие из них пока ещё не демонстрируют прогресса, — сказал Лампл. – Пока мы изучаем этот вопрос».
Шартон описывает, по меньшей мере, два способа, которыми их подход может помочь развить генераторы теорем. Во-первых, нейросеть может служить чем-то вроде ассистента математика, помогая разбираться с существующими задачами посредством поиска закономерностей в известных теоремах. Во-вторых, машина могла бы выдавать список потенциально доказуемых результатов, которые математики могли пропустить. «Мы считаем, что если она с интегрированием справляется, то и с доказательствами должна справиться», — сказал он.
Приложение, помогающее в поиске доказательств, может стать отличным подспорьем, и даже выйти за пределы того, что описывала команда из Facebook. Один из распространённых способов опровергнуть теорему – найти контрпример, показывающий, что она неверна. Когда-нибудь нейросети окажутся идеально подходящим для этой задачи инструментом: они будут искать неожиданные способы вставлять палки в колёса.
Ещё одна нерешённая задача, в решении которой такой подход может помочь, связана с наиболее неприятным аспектом нейросетей: никто не понимает, как они работают. С одной стороны в нейросеть входят обучающие данные, а с другой выходят предсказания, но что происходит в середине – конкретный процесс, позволяющий нейросети выдавать такие хорошие догадки – остаётся критически важным открытым вопросом.
Символьная математика, с другой стороны, определённо менее загадочная вещь. «Мы знаем, как работает математика, — сказал Шартон. – Используя определённые математические проблемы в качестве проверки того, где машины справляются, а где – нет, мы можем разобраться в том, как работают нейросети».
Вскоре они с Ламплом планируют начать подавать своим сетям на вход математические выражения и отслеживать, как их программа реагирует на небольшие изменения в этих выражениях. Разметка того, как изменения во входных данных изменяют выходные, может помочь раскрыть процесс работы нейросети.
Заремба считает, что такое понимание потенциально может помочь нам научить нейросети рассуждать, и реально понимать вопросы, на которые они ищут ответы. «В математике достаточно легко изменить данные и посмотреть, насколько хорошо справляется нейросеть, когда выражение меняется. Мы можем научиться рассуждать, а не просто получать ответ, — сказал он. – И тогда у нас появятся огромные возможности».