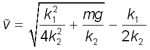Информационное моделирование что такое моделирование

Моделирование данных: зачем нужно и как реализовать

Моделирование данных ощутимо упрощает взаимодействие между разработчиками, аналитиками и маркетологами, как и сам процесс создания отчетов. Поэтому я перевела статью IBM Cloud Education о ценности моделирования и от себя добавила инфо о способах трансформации данных для моделирования.

Моделирование данных

Узнайте, как моделирование данных использует абстракцию для представления и лучшего понимания природы данных в информационной системе предприятия.

Что такое моделирование данных

Моделирование данных — это создание визуального представления о всей информационной системе либо ее части. Цель в том, чтобы проиллюстрировать типы данных, которые используются и хранятся в системе, отношения между этими типами данных, способы группировки и организации данных, их форматы и атрибуты.

Модели данных строятся на основе бизнес-потребностей. Правила и требования к модели данных определяются заранее на основе обратной связи с бизнесом, поэтому их можно включить в разработку новой системы или адаптировать к существующей.

Данные можно моделировать на различных уровнях абстракции. Процесс начинается со сбора бизнес-требований от заинтересованных сторон и конечных пользователей. Эти бизнес-правила затем преобразуются в структуры данных. Модель данных можно сравнить с дорожной картой, планом архитектора или любой формальной схемой, которая способствует более глубокому пониманию того, что разрабатывается.

Моделирование данных использует стандартизированные схемы и формальные методы. Это обеспечивает последовательный и предсказуемый способ управления данными в организации или за ее пределами.

В идеале модели данных — это живые документы, которые развиваются вместе с потребностями бизнеса. Они играют важную роль в поддержке бизнес-процессов и планировании ИТ-архитектуры и стратегии. Моделями данных можно делиться с поставщиками, партнерами и коллегами.

Преимущества моделирования данных

Моделирование упрощает просмотр и понимание взаимосвязей между данными для разработчиков, архитекторов данных, бизнес-аналитиков и других заинтересованных лиц. Кроме того, моделирование данных помогает:

Уменьшить количество ошибок при разработке программного обеспечения и баз данных.

Унифицировать документацию на предприятии.

Повысить производительность приложений и баз данных.

Упростить отображение данных по всей организации.

Улучшить взаимодействие между разработчиками и командами бизнес-аналитики.

Упростить и ускорить процесс проектирования базы данных на концептуальном, логическом и физическом уровнях.

Типы моделей данных

Разработка баз данных и информационных систем начинается с высокого уровня абстракции и с каждым шагом становится все точнее и конкретнее. В зависимости от степени абстракции модели данных можно разделить на три категории. Процесс начинается с концептуальной модели, переходит к логической модели и завершается физической моделью.

Концептуальные модели данных. Также они называются моделями предметной области и описывают общую картину: что будет содержать система, как она будет организована и какие бизнес-правила будут задействованы. Концептуальные модели обычно создаются в процессе сбора исходных требований к проекту. Как правило, они включают классы сущностей (вещи, которые бизнесу важно представить в модели данных), их характеристики и ограничения, отношения между сущностями, требования к безопасности и целостности данных. Любые обозначения обычно просты.

Логические модели данных уже не так абстрактны и предоставляют более подробную информацию о концепциях и взаимосвязях в рассматриваемой области. Они содержат атрибуты данных и показывают отношения между сущностями. Логические модели данных не определяют никаких технических требований к системе. Этот этап часто пропускается в agile или DevOps-практиках. Логические модели данных могут быть полезны для проектов, ориентированных на данные по своей природе. Например, для проектирования хранилища данных или разработки системы отчетности.

Физические модели данных представляют схему того, как данные будут храниться в базе. По сути, это наименее абстрактные из всех моделей. Они предлагают окончательный дизайн, который может быть реализован как реляционная база данных, включающая ассоциативные таблицы, которые иллюстрируют отношения между сущностями, а также первичные и внешние ключи для связи данных.

Процесс моделирования данных

Моделирование данных начинается с договоренности о том, какие символы используются для представления данных, как размещаются модели и как передаются бизнес-требования. Это формализованный рабочий процесс, включающий ряд задач, которые должны выполняться итеративно. Сам процесс обычно выглядят так:

Определите сущности. На этом этапе идентифицируем объекты, события или концепции, представленные в наборе данных, который необходимо смоделировать. Каждая сущность должна быть целостной и логически отделенной от всех остальных.

Определите ключевые свойства каждой сущности. Каждый тип сущности можно отличить от всех остальных, поскольку он имеет одно или несколько уникальных свойств, называемых атрибутами. Например, сущность «клиент» может обладать такими атрибутами, как имя, фамилия, номер телефона и т.д. Сущность «адрес» может включать название и номер улицы, город, страну и почтовый индекс.

Определите связи между сущностями. Самый ранний черновик модели данных будет определять характер отношений, которые каждая сущность имеет с другими. В приведенном выше примере каждый клиент «живет по» адресу. Если бы эта модель была расширена за счет включения сущности «заказы», ​​каждый заказ также был бы отправлен на адрес. Эти отношения обычно документируются с помощью унифицированного языка моделирования (UML).

Полностью сопоставьте атрибуты с сущностями. Это гарантирует, что модель отражает то, как бизнес будет использовать данные. Широко используются несколько формальных шаблонов (паттернов) моделирования данных. Объектно-ориентированные разработчики часто применяют шаблоны для анализа или шаблоны проектирования, в то время как заинтересованные стороны из других областей бизнеса могут обратиться к другим паттернам.

Назначьте ключи по мере необходимости и определите степень нормализации. Нормализация — это метод организации моделей данных, в которых числовые идентификаторы (ключи) назначаются группам данных для установления связей между ними без повторения данных. Например, если каждому клиенту назначен ключ, этот ключ можно связать как с его адресом, так и с историей заказов, без необходимости повторять эту информацию в таблице с именами клиентов. Нормализация помогает уменьшить объем дискового пространства, необходимого для базы данных, но может сказываться на производительности запросов.

Завершите и проверьте модель данных. Моделирование данных — это итеративный процесс, который следует повторять и совершенствовать под потребности бизнеса.

Типы моделирования данных

Моделирование данных развивалось вместе с системами управления базами данных (СУБД), при этом типы моделей усложнялись по мере роста потребностей предприятий в хранении данных.

Иерархические модели данных представляют отношения «один ко многим» в древовидном формате. В модели этого типа каждая запись имеет единственный корень или родительский элемент, который сопоставляется с одной или несколькими дочерними таблицами. Эта модель была реализована в IBM Information Management System (IMS) ​​в 1966 году и быстро нашла широкое применение, особенно в банковской сфере. Хотя этот подход менее эффективен, чем недавно разработанные модели баз данных, он все еще используется в системах расширяемого языка разметки (XML) и географических информационных системах (ГИС).

Реляционные модели данных были предложены исследователем IBM Э. Ф. Коддом в 1970 году. Они до сих пор встречаются во многих реляционных базах данных, обычно используемых в корпоративных вычислениях. Реляционное моделирование не требует детального понимания физических свойств используемого хранилища данных. В нем сегменты данных объединяются с помощью таблиц, что упрощает базу данных.

Реляционные базы данных часто используют язык структурированных запросов (SQL) для управления данными. Эти базы подходят для поддержания целостности данных и минимизации избыточности. Они часто используются в кассовых системах, а также для других типов обработки транзакций.

В ER-моделях данных используют диаграммы для представления взаимосвязей между сущностями в базе данных. ER-модель представляет собой формальную конструкцию, которая не предписывает никаких графических средств её визуализации. В качестве стандартной графической нотации, с помощью которой можно визуализировать ER-модель, была предложена диаграмма «сущность-связь» (Entity-Relationship diagram). Однако для визуализации ER-моделей могут использоваться и другие графические нотации, либо визуализация может вообще не применяться (например, только текстовое описание).

Объектно-ориентированные модели данных получили распространение как объектно-ориентированное программирование и стали популярными в середине 1990-х годов. Вовлеченные «объекты» — это абстракции сущностей реального мира. Объекты сгруппированы в иерархии классов и имеют связанные черты. Объектно-ориентированные базы данных могут включать таблицы, но могут также поддерживать более сложные связи. Этот подход часто используется в мультимедийных и гипертекстовых базах данных.

Размерные модели данных разработал Ральф Кимбалл для быстрого поиска данных в хранилище. Реляционные и ER-модели делают упор на эффективное хранение и уменьшают избыточность данных, а размерные модели упорядочивает данные таким образом, чтобы легче было извлекать информацию и создавать отчеты. Это моделирование обычно используется в системах OLAP.

Две популярные размерные модели данных — это схемы «звезда» и «снежинка». В схеме «звезда» данные организованы в факты (измеримые элементы) и измерения (справочная информация), где каждый факт окружен связанными с ним измерениями в виде звездочки. Схема «снежинка» напоминает схему «звезда», но включает дополнительные слои связанных измерений, что усложняет схему ветвления.

Инструменты для моделирования данных

Сегодня широко используются многочисленные коммерческие и CASE-решения с открытым исходным кодом, в том числе различные инструменты моделирования данных, построения диаграмм и визуализации. Вот несколько примеров:

erwin Data Modeler — это инструмент моделирования данных, основанный на языке IDEF1X, который теперь поддерживает и другие нотации, включая нотацию для размерного моделирования.

Enterprise Architect — это инструмент визуального моделирования и проектирования, который поддерживает моделирование корпоративных информационных систем и архитектур, программных приложений и баз данных. Он основан на объектно-ориентированных языках и стандартах.

ER/Studio — это программа для проектирования баз данных, совместимая с некоторыми из самых популярных СУБД. Она поддерживает как реляционное, так и размерное моделирование данных.

Бесплатные инструменты моделирования данных включают решения с открытым исходным кодом, такие как Open ModelSphere.

Для того, чтобы преобразовать данные в структуру, которая соответствует требованиям модели, можно использовать встроенный механизм регулярных запросов, которые выполняются в Google BigQuery, Scheduled Queries и AppScript. Их легко можно освоить, потому что это привычный SQL, но проводить отладку в Scheduled Queries практически нереально. Особенно, если это какой-то сложный запрос или каскад запросов.

Есть специализированные инструменты для управления SQL-запросами, например, dbt и Dataform.

dbt (data build tool) — это фреймворк с открытым исходным кодом для выполнения, тестирования и документирования SQL-запросов, который позволяет привнести элемент программной инженерии в процесс анализа данных. Он помогает оптимизировать работу с SQL-запросами: использовать макросы и шаблоны JINJA, чтобы не повторять в сотый раз одни и те же фрагменты кода.

Главная проблема, которую решают специализированные инструменты — это уменьшение времени, необходимого на поддержку и обновление. Это достигается за счет удобства отладки.

Источник

Учитель информатики

Сайт учителя информатики. Технологические карты уроков, Подготовка к ОГЭ и ЕГЭ, полезный материал и многое другое.

§ 9. Информационное моделирование

Информатика. 6 класса. Босова Л.Л. Оглавление

Модели объектов и их назначение

Стремясь познать объекты окружающего мира, человек взаимодействует с существующими объектами и создаёт новые объекты.

Одним из методов познания объектов окружающего мира является моделирование, состоящее в создании и исследовании «заместителей» реальных объектов. «Объект-заместитель» принято называть моделью, а исходный объект — прототипом или оригиналом.

Например, в разговоре мы замещаем реальные объекты их именами, оформители витрин используют манекен — модель человеческой фигуры, конструкторы строят модели самолётов и автомобилей, а архитекторы — макеты зданий, мостов и парков. Моделью является любое наглядное пособие, используемое на уроках в школе: глобус, муляж, карта, схема, таблица и т. п. (рис. 23).

Что общего у всех моделей? Какими свойствами они обладают?

Во-первых, модель не является точной копией объекта-оригинала: она отражает только часть его свойств, отношений и особенностей поведения. Например, на манекен можно надеть костюм, но с ним нельзя поговорить. Модель автомобиля может быть без мотора, а макет дома — без электропроводки и водопровода.

Во-вторых, поскольку любая модель всегда отражает только часть признаков оригинала, то можно создавать и использовать разные модели одного и того же объекта. Например: мяч может воспроизвести только одно свойство Земли — её форму; обычный глобус отражает, кроме того, расположение материков; а глобус, входящий в состав действующей модели Солнечной системы, — ещё и траекторию движения Земли вокруг Солнца.

Чем больше признаков объекта отражает модель, тем она полнее. Однако отразить в модели все свойства объекта-оригинала невозможно, а чаще всего и не нужно. Ведь при создании модели человек, как правило, преследует вполне определенную цель и стремится наиболее полно отразить только те признаки объектов, которые кажутся ему важными, существенными для реализации этой цели. Если, например, модель самолёта создается для коллекции, то в ней воспроизводится внешний вид самолета, а не его лётные характеристики.

От цели моделирования зависят требования к модели: какие именно признаки объекта-оригинала она должна отражать.

Отразить в модели признаки оригинала можно одним из двух способов.

Во-первых, признаки можно скопировать, воспроизвести. Такую модель называют натурной (материальной). Примерами натурных моделей являются муляжи и макеты — уменьшенные или увеличенные копии, воспроизводящие внешний вид объекта моделирования (глобус), его структуру (модель Солнечной системы) или поведение (радиоуправляемая модель автомобиля).

Во-вторых, признаки оригинала можно описать на одном из языков кодирования информации — дать словесное описание, привести формулу, схему или чертёж. Такую модель называют информационной.

Модели используются человеком для:

Разнообразие информационных моделей

Объект-оригинал можно заменить набором его признаков.

Набор признаков, содержащий всю необходимую информацию об исследуемом объекте или процессе, называют информационной моделью.

В таблице 2 приведён пример информационной модели дачного дома — карточки из каталога, по которому заказчик строительной компании может выбрать подходящий проект. Каждая карточка в каталоге содержит величины и их значения, определяющие свойства дома.

Все названия свойств в информационных моделях — это всегда знаковые элементы, потому что название может быть выражено только знаками. А вот значения величин могут нести как знаковую, так и образную информацию. Например, в таблице 2 значение величины «внешний вид» выражено образным элементом (рисунком), а значения остальных величин выражены с помощью знаков (цифр, букв).

Информационные модели представляют объекты и процессы в образной или знаковой форме. По способу представления различают следующие виды информационных моделей — рис. 24.

Образные информационные модели (рисунки, фотографии и др.) представляют собой зрительные образы объектов, зафиксированные на каком-либо носителе информации (например, на бумаге).

Много информации дают специалистам полученные со спутников фотографии поверхности Земли (рис. 25).

Широко используются образные информационные модели в образовании (иллюстрации в учебниках (рис. 26), учебные плакаты по различным предметам) и науках, где требуется классификация объектов по их внешним признакам (в ботанике, биологии, палеонтологии и др.).

Знаковая информационная модель может быть представлена в форме текста на естественном языке, формулы (например, площади прямоугольника S = axb) или программы на специальном языке программирования и т. д.

В смешанных информационных моделях одновременно используются образные и знаковые элементы.

Примерами смешанных информационных моделей могут служить географические карты, графики, диаграммы и пр. На рисунке 27 приведён пример модели одноклеточной водоросли хламидомонады. Нарисованные части водоросли — образные элементы этой модели, а надписи снизу и справа от рисунка — знаковые элементы.

Самое главное

Модель — это объект, который используется в качестве «заместителя», представителя другого объекта (оригинала) с определённой целью. Модель не является точной копией объекта-оригинала: она отражает только часть его свойств, отношений и особенностей поведения. Можно создавать и использовать разные модели одного и того же объекта.

Процесс создания и использования модели называют моделированием.

Различают натурные и информационные модели. Натурные модели — реальные предметы, в уменьшенном или увеличенном виде воспроизводящие внешний вид, структуру или поведение объекта моделирования.

Набор признаков, содержащий всю необходимую информацию об исследуемых объектах и процессах, называют информационной моделью.

Источник

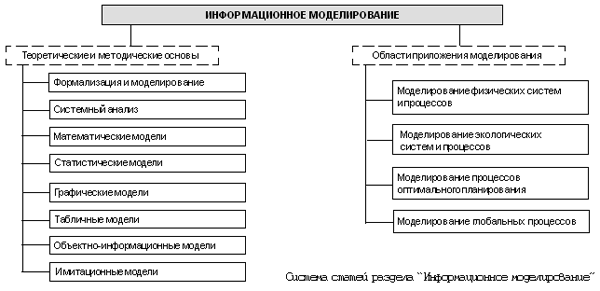
IV. Информационное моделирование

Список статей

1. Графические модели

2. Имитационные модели

3. Математические модели

4. Моделирование процессов оптимального планирования

5. Моделирование глобальных процессов

6. Моделирование физических систем и процессов

7. Моделирование экологических систем и процессов

8. Объектно-информационные модели

9. Системный анализ

10. Статистические модели

11. Табличные модели

12. Формализация и моделирование

В школьном курсе информатики традиционно присутствует содержательная линия формализации и моделирования. Понятие модели относится к фундаментальным общенаучным понятиям, а моделирование — это метод познания действительности, используемый различными науками.

Практически во всех естественных и социальных науках построение и использование моделей является мощным орудием исследований. Реальные объекты и процессы бывают столь многогранны и сложны, что лучшим способом их изучения оказывается построение модели, отображающей лишь какую-то часть реальности и потому многократно более простой, чем эта реальность. Предметом исследования и разработки информатики является методология информационного моделирования, связанная с использованием компьютерной техники и технологий. В этом смысле говорят о компьютерном моделировании. Межпредметное значение информатики в значительной степени проявляется именно через внедрение компьютерного моделирования в различные научные и прикладные области: физику и технику, биологию и медицину, экономику, управление и многие другие.

Компьютерное моделирование включает в себя процесс реализации информационной модели на компьютере и исследование с помощью этой модели объекта моделирования — проведение вычислительного эксперимента. С помощью компьютерного моделирования решаются многие научные и производственные задачи.

Информационное моделирование связано с формализацией данных об объекте моделирования (см. “Формализация и моделирование”). Построение информационной модели начинается с определения целей моделирования и анализа объекта моделирования как сложной системы, в которой требуется выделить отражаемые в модели свойства и отношения между ними (см. “Системный анализ”). Информационные модели различаются по форме представления информации об объекте моделирования. Математические модели используют язык математики для представления объекта моделирования. Отдельной разновидностью математических моделей являются статистические модели — ориентированные на обработку массовых данных (например, опросов населения), в которых имеется элемент случайности. Данные об объекте моделирования, организованные в табличной форме, составляют табличную модель. Графические средства используются для построения графических моделей. Возникший в конце прошлого столетия объектно-ориентированный подход к программированию породил новую парадигму в информационном моделировании: объектно-информационное моделирование. Компьютерные модели, воспроизводящие поведение сложных систем, для описания которых нет однозначного математического аппарата, называются имитационными моделями.

Компьютерное информационное моделирование используется для описания и анализа процессов разнообразной природы. Наибольший опыт в этом отношении имеют физические науки (см. “Моделирование физических систем и процессов”). Компьютерное моделирование помогает решать важные проблемы экологии (см. “Моделирование экологических систем и процессов”). Большую роль играет информационное моделирование в экономике и управлении. Важнейшими задачами этой области являются задачи планирования (см. “Моделирование процессов оптимального планирования”). Средствами компьютерного моделирования ученые пытаются решить даже такую глобальную проблему, как судьбы человеческой цивилизации (см. “Моделирование глобальных процессов”).

1. Графические модели

Разнообразие графических моделей достаточно велико. Рассмотрим некоторые из них.

Наглядным средством отображения состава и структуры систем (см. “Системология”) являются графы.

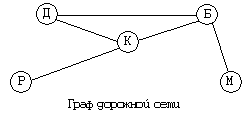
Рассмотрим пример. Имеется словесное описание некоторой местности: “Наш район состоит из пяти поселков: Дедкино, Бабкино, Репкино, Кошкино и Мышкино. Автомобильные дороги проложены между: Дедкино и Бабкино, Дедкино и Кошкино, Бабкино и Мышкино, Бабкино и Кошкино, Кошкино и Репкино”. По такому описанию довольно трудно представить себе эту местность. Гораздо легче та же информация воспринимается с помощью схемы (см. рисунок). Это не карта местности. Здесь не выдержаны направления по сторонам света, не соблюден масштаб. На этой схеме отражен лишь факт существования пяти поселков и дорожной связи между ними. Такая схема, отображающая элементный состав системы и структуру связей, называется графом.

Составными частями графа являются вершины и ребра. На рисунке вершины изображены кружками — это элементы системы, а ребра изображены линиями — это связи (отношения) между элементами. Глядя на этот граф, легко понять структуру дорожной системы в данной местности.

Построенный граф позволяет, например, ответить на вопрос: через какие поселки надо проехать, чтобы добраться из Репкино в Мышкино? Видно, что есть два возможных пути: 1) Р К Б М и) Р К Д Б М. Можно ли отсюда сделать вывод, что 1-й путь короче 2-го? Нет, нельзя. Данный граф не содержит количественных характеристик. Это не карта, где соблюдается масштаб и есть возможность измерить расстояние.

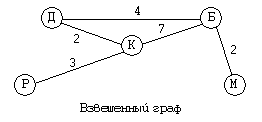
Граф, приведенный на следующем рисунке, содержит количественные характеристики. Числа около ребер обозначают длины дорог в километрах. Это пример взвешенного графа. Взвешенный граф может содержать количественные характеристики не только связей, но и вершин. Например, в вершинах может быть указано население каждого поселка. Согласно данным взвешенного графа, оказывается, что первый путь длиннее второго.

Подобные графы еще называют сетью. Для сети характерна возможность множества различных путей перемещения по ребрам между некоторыми парами вершин. Для сетей также характерно наличие замкнутых путей, которые называются циклами. В данном случае имеется цикл: К Д Б К.

На рассмотренных схемах каждое ребро обозначает наличие дорожной связи между двумя пунктами. Но дорожная связь действует одинаково в обе стороны: если по дороге можно проехать от Б к М, то по ней же можно проехать и от М к Б (предполагаем, что действует двустороннее движение). Такие графы являются неориентированными, а их связи называют симметричными.

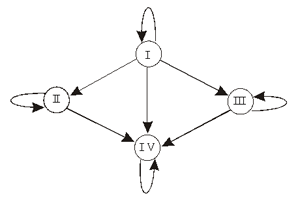
Качественно иной пример графа изображен на следующем рисунке.

Граф совместимости групп крови

Этот пример относится к медицине. Известно, что у разных людей кровь отличается по группе. Существуют четыре группы крови. Оказывается, что при переливании крови от одного человека к другому не все группы совместимы. Граф показывает возможные варианты переливания крови. Группы крови — это вершины графа с соответствующими номерами, а стрелки указывают на возможность переливания одной группы крови человеку с другой группой крови. Например, из этого графа видно, что кровь I группы можно переливать любому человеку, а человек с I группой крови воспринимает только кровь своей группы. Видно также, что человеку с IV группой крови можно переливать любую, но его собственную кровь можно переливать только в ту же группу.

Связи между вершинами данного графа несимметричны и поэтому изображаются направленными линиями со стрелками. Такие линии принято называть дугами (в отличие от ребер неориентированных графов). Граф с такими свойствами называется ориентированным. Линия, выходящая и входящая в одну и ту же вершину, называется петлей. В данном примере присутствуют четыре петли.

Нетрудно понять преимущества изображения модели системы переливания крови в виде графа по сравнению со словесным описанием тех же самых правил. Граф легко воспринимается и запоминается.

Весьма распространенным типом систем являются системы с иерархической структурой. Иерархическая структура естественным образом возникает, когда объекты или некоторые их свойства находятся в отношении соподчинения (вложения, наследования). Как правило, иерархическую структуру имеют системы административного управления, между элементами которых установлены отношения подчиненности. Например: директор завода — начальники цехов — начальники участков — бригадиры — рабочие. Иерархическую структуру имеют также системы, между элементами которых существуют отношения вхождения одних в другие.

Граф иерархической структуры называется деревом. Основным свойством дерева является то, что между любыми двумя его вершинами существует единственный путь. Деревья не содержат циклов и петель.

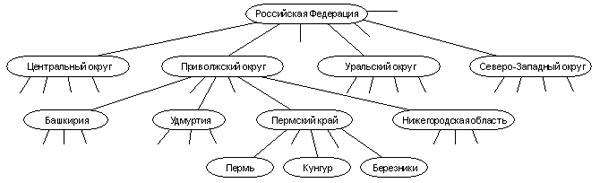
Посмотрите на граф, отражающий иерархическую административную структуру нашего государства: Российская Федерация делится на семь административных округов; округа делятся на регионы (области и национальные республики), в состав которых входят города и другие населенные пункты. Такой граф называется деревом.

Дерево административной структуры РФ

У дерева существует одна главная вершина, которая называется корнем дерева. Эта вершина изображается вверху; от нее идут ветви дерева. От корня начинается отсчет уровней дерева. Вершины, непосредственно связанные с корнем, образуют первый уровень. От них идут связи к вершинам второго уровня и т.д. Каждая вершина дерева (кроме корня) имеет одну исходную вершину на предыдущем уровне и может иметь множество порожденных вершин на следующем уровне. Такой принцип связи называется “один ко многим”. Вершины, которые не имеют порожденных, называются листьями (на нашем графе это вершины, обозначающие города).

Общую цель научной графики можно сформулировать так: сделать невидимое и абстрактное “видимым”. Последнее слово заключено в кавычки, так как эта “видимость” часто весьма условна. Можно ли увидеть распределение температуры внутри неоднородно нагретого тела сложной формы без введения в него сотен микродатчиков, т.е., по существу, его разрушения? — Да, можно, если есть соответствующая математическая модель и, что очень важно, договоренность о восприятии определенных условностей на рисунке. Можно ли увидеть распределение металлических руд под землей без раскопок? Строение поверхности чужой планеты по результатам радиолокации? На эти и множество других вопросов ответ — да, можно, с помощью компьютерной графики и предшествующей ей математической обработки.

Более того, можно “увидеть” и то, что, строго говоря, вообще плохо соответствует слову “видеть”. Так, возникшая на стыке химии и физики наука — квантовая химия — дает нам возможность “увидеть” строение молекулы. Эти изображения — верх абстракции и системы условностей, так как в атомном мире обычные наши понятия о частицах (ядрах, электронах и т.п.) принципиально неприменимы. Однако многоцветное “изображение” молекулы на экране компьютера для тех, кто понимает всю меру его условности, приносит большую пользу, чем тысячи чисел, являющихся результатами вычислений.

Изолинии

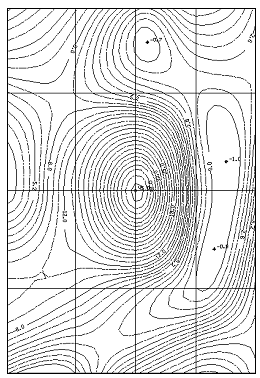
Стандартным приемом обработки результатов вычислительного эксперимента является построение линий (поверхностей), называемых изолиниями (изоповерхностями), вдоль которых некоторая функция имеет постоянное значение. Это очень распространенный прием визуализации характеристик некоторого скалярного поля в приближении сплошной среды: изотермы — линии равной температуры, изобары — линии равного давления, изолинии функции тока жидкости или газа, по которым легко можно представить себе их потоки, изолинии численностей экологической популяции на местности, изолинии концентрации вредных примесей в окружающей среде и т.д.

На рисунке изображены изолинии функции тока неравномерно нагретой жидкости в прямоугольной области течения. По этой картине можно наглядно судить о направлении потоков течения и их интенсивности.

Условные цвета, условное контрастирование

Еще один интересный прием современной научной графики — условная раскраска. Она находит широчайшее применение в самых разных приложениях науки и представляет собой набор приемов по максимально удобной визуализации результатов компьютерного моделирования.

В различных исследованиях температурных полей встает проблема наглядного представления результатов, например, температур на метеорологических картах. Для этого можно рисовать изотермы на фоне карты местности. Но можно добиться еще большей наглядности, учитывая, что большинству людей свойственно воспринимать красный цвет как “горячий”, синий — как “холодный”. Переход по спектру от красного к синему отражает промежуточные значения температур.

То же самое можно делать при иллюстрации температурного поля и на поверхности обрабатываемой на станке детали, и на поверхности далекой планеты.

При моделировании сложных органических молекул компьютер может выдавать результаты в виде многоцветной картины, на которой атомы водорода изображены одним цветом, углерода — другим и т.д., причем атом представлен шариком (кружочком), в пределах которого плотность цвета меняется в соответствии с распределением электронной плотности. При поиске полезных ископаемых методами аэрофотосъемки с самолетов или космических спутников компьютеры строят условные цветовые изображения распределений плотности под поверхностью Земли.

Изображения в условных цветах и контрастах — мощнейший прием научной графики. Он позволяет понять строение не только плоских, но и объемных (трехмерных) объектов, дает в руки исследователя один из замечательных методов познания.

Методические рекомендации

Не следует путать изучение графического информационного моделирования с изучением технологий обработки графической информации. Когда ученики приступают к изучению моделирования, то обычно они уже знакомы с базовыми технологиями компьютерной графики: умеют пользоваться простыми графическими редакторами, умеют строить диаграммы в табличном процессоре или иной подходящей программе.

Построение простых графических моделей в форме графов и иерархических структур уместно уже в базовом курсе информатики в рамках изучения темы “Формализация и моделирование”. Построение генеалогического дерева семьи, иерархической системы школьного управления и т.п. является относительно несложным занятием, доступным большинству учащихся. При этом уместно использовать иллюстративные возможности систем компьютерной графики.

Что же касается самостоятельной реализации моделей научной графики через программирование, то это — материал повышенной трудности, практическая отработка которого уместна в профильном курсе информатики или в рамках элективного курса, направленного на углубленное изучение моделирования физических и других процессов.

2. Имитация модели

Имитационная модель воспроизводит поведение сложной системы взаимодействующих элементов. Для имитационного моделирования характерно наличие следующих обстоятельств (одновременно всех или некоторых из них):

· объект моделирования — сложная неоднородная система;

· в моделируемой системе присутствуют факторы случайного поведения;

· требуется получить описание процесса, развивающегося во времени;

· принципиально невозможно получить результаты моделирования без использования компьютера.

Состояние каждого элемента моделируемой системы описывается набором параметров, которые хранятся в памяти компьютера в виде таблиц. Взаимодействия элементов системы описываются алгоритмически. Моделирование осуществляется в пошаговом режиме. На каждом шаге моделирования изменяются значения параметров системы. Программа, реализующая имитационную модель, отражает изменение состояния системы, выдавая значения ее искомых параметров в виде таблиц по шагам времени или в последовательности происходящих в системе событий. Для визуализации результатов моделирования часто используется графическое представление, в т.ч. анимированное.

Имитационная модель основана на подражании реальному процессу (имитации). Например, моделируя изменение (динамику) численности микроорганизмов в колонии, можно рассматривать много отдельных объектов и следить за судьбой каждого из них, ставя определенные условия для его выживания, размножения
и т.д. Эти условия обычно задаются в вербальной форме. Например: по истечении некоторого промежутка времени микроорганизм делится на две части, а по прошествии другого (большего) временноRго отрезка — погибает. Выполнение описанных условий алгоритмически реализуется в модели.

Другой пример: моделирование движения молекул в газе, когда каждая молекула представляется в виде шарика с определенным направлением и скоростью движения. Взаимодействие двух молекул или молекулы со стенкой сосуда происходит согласно законам абсолютно-упругого столкновения и легко описывается алгоритмически. Получение интегральных (общих, усредненных) характеристик системы производится на уровне статистической обработки результатов моделирования.

Такой компьютерный эксперимент фактически претендует на воспроизведение натурного эксперимента. На вопрос: “Зачем это нужно делать?” можно дать следующий ответ: имитационное моделирование позволяет выделить “в чистом виде” следствия гипотез, заложенных в представления о микрособытиях (т.е. на уровне элементов системы), избавив их от неизбежного в натурном эксперименте влияния других факторов, о которых мы можем даже не подозревать. Если такое моделирование включает и элементы математического описания процессов на микроуровне, и если исследователь при этом не ставит задачу поиска стратегии регулирования результатов (например, управления численностью колонии микроорганизмов), то отличие имитационной модели от математической (дескриптивной) оказывается достаточно условным.

Приведенные выше примеры имитационных моделей (эволюция колонии микроорганизмов, движение молекул в газе) приводят к детерминированному описанию систем. В них отсутствуют элементы вероятности, случайности событий в моделируемых системах. Рассмотрим пример моделирования системы, обладающей этими качествами.

Кому не случалось стоять в очереди и с нетерпением прикидывать, успеет ли он сделать покупку (или заплатить за квартиру, покататься на карусели и т.д.) за некоторое имеющееся в его распоряжении время? Или, пытаясь позвонить по телефону в справочную и натыкаясь несколько раз на короткие гудки, нервничать и оценивать — дозвонюсь или нет? Из таких “простых” проблем в начале XX века родилась новая отрасль математики — теория массового обслуживания, использующая аппарат теории вероятностей и математической статистики, дифференциальных уравнений и численных методов. Впоследствии выяснилось, что эта теория имеет многочисленные выходы в экономику, военное дело, организацию производства, биологию и экологию и т.д.

Компьютерное моделирование при решении задач массового обслуживания, реализуемое в виде метода статистических испытаний (метода Монте-Карло), играет важную роль. Возможности аналитических методов решения реально возникающих задач массового обслуживания весьма ограничены, в то время как метод статистических испытаний универсален и относительно прост.

Рассмотрим простейшую задачу этого класса. Имеется магазин с одним продавцом, в который случайным образом входят покупатели. Если продавец свободен, то он начинает обслуживать покупателя сразу, если зашло одновременно несколько покупателей — выстраивается очередь. Есть немало других аналогичных ситуаций:

· ремонтная зона в автохозяйстве и автобусы, сошедшие с линии из-за поломки;

· травмпункт и больные, пришедшие на прием по случаю травмы (т.е. без системы предварительной записи);

· телефонная станция с одним входом (или одной телефонисткой) и абоненты, которых при занятом входе ставят в очередь (такая система иногда практикуется);

· сервер локальной сети и персональные машины на рабочем месте, которые шлют сообщение серверу, способному воспринять разом и обработать не более одного сообщения.

Процесс прихода покупателей в магазин — случайный процесс. Промежутки времени между приходами любой последовательной пары покупателей — независимые случайные события, распределенные по некоторому закону, который может быть установлен лишь путем многочисленных наблюдений (либо для моделирования взят некоторый его правдоподобный вариант). Второй случайный процесс в этой задаче, никак не связанный с первым, — длительность обслуживания каждого из покупателей.

Целью моделирования систем такого вида является получение ответа на ряд вопросов. Относительно простой вопрос — какое в среднем время придется стоять в очереди при заданных законах распределения указанных выше случайных величин? Более сложный вопрос: каково распределение времен ожидания обслуживания в очереди? Не менее сложный вопрос: при каких соотношениях параметров входных распределений наступит кризис, при котором очередь до вновь вошедшего покупателя не дойдет никогда? Если задуматься над этой относительно простой задачей, возможные вопросы будут множиться.

Способ моделирования выглядит в общих чертах так. Используемые математические формулы — законы распределения исходных случайных величин; используемые числовые константы — эмпирические параметры, входящие в эти формулы. Не решается никаких уравнений, которые использовались бы при аналитическом исследовании данной задачи. Вместо этого происходит имитация очереди, разыгрываемая с помощью компьютерных программ, генерирующих случайные числа с заданными законами распределения. Затем производится статистическая обработка совокупности полученных значений величин, определяемых заданными целями моделирования. Например, находится оптимальное количество продавцов для разных периодов времени работы магазина, которое обеспечит отсутствие очередей. Математический аппарат, который здесь используется, называется методами математической статистики.

В статье “Моделирование экологических систем и процессов” 2 описан другой пример имитационного моделирования: одна из многих моделей системы “хищник—жертва”. Особи видов, находящихся в указанных отношениях, по определенным правилам, содержащим элементы случайности, перемещаются, хищники съедают жертв, и те и другие размножаются и т.д. Такая модель не содержит никаких математических формул, но требует статистической обработки результатов.

Пример алгоритма детерминированной имитационной модели

Рассмотрим имитационную модель эволюции популяции живых организмов, известную под названием “Жизнь”, которую легко реализовать на любом языке программирования.

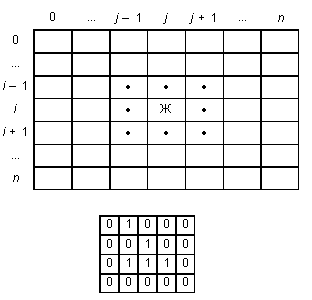
Для построения алгоритма игры рассмотрим квадратное поле из n + 1 столбцов и строк с обычной нумерацией от 0 до n. Крайние граничные столбцы и строки для удобства определим как “мертвую зону”, они играют лишь вспомогательную роль.

Для любой внутренней клетки поля с координатами (i, j) можно определить 8 соседей. Если клетка “живая”, ее закрашиваем, если клетка “мертвая”, она пустая.

Зададим правила игры. Если клетка (i, j) “живая” и ее окружает более трех “живых” клеток, она погибает (от перенаселения). “Живая” клетка также погибает, если в ее окружении находится менее двух “живых” клеток (от одиночества). “Мертвая” клетка оживает, если вокруг нее появляются три “живые” клетки.

Для удобства введем двумерный массив A[0..n, 0..n], элементы которого принимают значение 0, если соответствующая клетка пустая, и 1, если клетка “живая”. Тогда алгоритм определения состояния клетки с координатой (i, j) можно определить следующим образом:

+ А[I + 1, J] + А[I + 1, J + 1] +

(S Контуры обратных связей чсленности населения, капитала, сельскохозяйственного производства и загрязнения окружающей среды

Понятия положительной и отрицательной обратной связи взяты из теории автоматического регулирования (раздела кибернетики). Причинно-следственная связь между двумя элементами называется отрицательной, если изменение одного элемента передается второму, возвращается от него к первому и изменяет его в направлении, противоположном первоначальному (подавляет), и положительной, если это изменение, возвращаясь к первому, усиливает его. Если элементов не два, а больше, то говорят о контуре обратной связи, через которую сигнал проходит по кругу, возвращаясь к источнику и влияя на него.

Некоторый набор таких рисунков графически исчерпывает модель WORLD. Однако за каждой стрелкой — первичные взаимосвязи, а за каждой из них — уравнения, в которые входит ряд параметров. Фактически именно значения этих параметров и определяют результаты, поэтому к их анализу привлекаются как многочисленные узкие специалисты, так и многие эмпирические (статистические) данные, собранные в десятках справочников, отчетов ООН и отдельных государств. Количество взаимосвязанных переменных в модели WORLD-3 равно 225, параметров — еще больше.

Результаты глобального моделирования

Опубликованные “сценарии” развития человечества, следующие из моделей WORLD, охватывают промежуток времени от 1900 до 2100 года. Первые 100 лет, уже прошедшие, позволяют “настраивать” модель, определить степень ее достоверности.

Первый из сценариев основан на гипотезе, что все будет развиваться без серьезных изменений, глобальных политических катаклизмов, без особых усилий по сохранению ресурсов и уменьшению загрязнения окружающей среды. Модель предсказывает катастрофические результаты такого развития.

Вместе с тем модель WORLD позволяет найти пути регулируемого развития, которое ведет к плавному (“сигмоидному”) поведению основных переменных. Этот путь связан с самоограничениями и переходом на усовершенствованные промышленные и сельскохозяйственные технологии.

Постановка задачи оптимального планирования

Планирование — важнейший этап экономической и управленческой деятельности. Объектом планирования может быть деятельность подразделения или всего предприятия, отрасли промышленности или сельского хозяйства, региона, наконец, государства.

Постановка задачи планирования в общем случае выглядит следующим образом:

· имеются некоторые плановые показатели: X, Y, …;

· имеются некоторые ресурсы: R1, R2, …, за счет которых эти плановые показатели могут быть достигнуты;

· имеется определенная стратегическая цель, зависящая от значений плановых показателей, на которую следует ориентировать планирование.

Задача оптимального планирования заключается в определении значений плановых показателей с учетом ограниченности ресурсов при условии достижения стратегической цели.

Приведем примеры. Пусть объектом планирования является детский сад. Ограничимся лишь двумя плановыми показателями: числом детей и числом воспитателей. Основными ресурсами деятельности детского сада являются размер финансирования и размер помещения. А каковы стратегические цели? Естественно, одной из них является сохранение и укрепление здоровья детей. Количественной мерой этой цели является минимизация заболеваемости воспитанников детского сада.

Другой пример: планирование экономической деятельности государства. Безусловно, это слишком сложная задача для детального анализа. Плановых показателей очень много: это производство различных видов промышленной и сельскохозяйственной продукции, подготовка специалистов, выработка электроэнергии, размер зарплаты работников бюджетной сферы и многое другое. К ресурсам относятся: количество работоспособного населения, бюджет государства, природные ресурсы, энергетика, возможности транспортных систем и пр. Разумеется, каждый из этих видов ресурсов ограничен. Кроме того, важнейшим ресурсом является время, отведенное на выполнение плана.

Вопрос о стратегических целях в этом случае очень сложен. У государства их много, но в разные периоды истории приоритеты могут меняться. Например, в военное время главной целью является максимальная обороноспособность, военная мощь страны. В мирное время в современном цивилизованном государстве приоритетной целью должно быть достижение максимального уровня жизни населения.

Решение задач оптимального планирования чаще всего является сложным и недоступным при использовании лишь человеческого опыта (эмпирических методов). Для решения таких задач строится математическая модель, устанавливающая связь между параметрами задачи. Следовательно, оптимальное планирование осуществляется путем применения математического моделирования. Как правило, такие модели для реальных ситуаций не поддаются аналитическому решению, поэтому используются численные методы решения, реализуемые на компьютере.

Пример математической модели оптимального планирования

Рассмотрим простой пример, с помощью которого можно получить представление об одном из классов задач оптимального планирования.

Школьный кондитерский цех готовит пирожки и пирожные. В силу ограниченности емкости склада за день можно приготовить в совокупности не более 700 изделий. Рабочий день в кондитерском цехе длится 8 часов. Поскольку производство пирожных более трудоемко, то, если выпускать только их, за день можно произвести не более 250, пирожков же можно произвести 1000 (если при этом не выпускать пирожных). Стоимость пирожного вдвое выше, чем пирожка. Требуется составить дневной план производства, обеспечивающий кондитерскому цеху наибольшую выручку.

Сформулируем эту задачу математически. Плановыми показателями являются:

x — дневной план выпуска пирожков;

y — дневной план выпуска пирожных.

Ресурсы производства — это:

· длительность рабочего дня — 8 часов;

· вместимость складского помещения — 700 мест.

К двум полученным неравенствам следует добавить условия положительности значений величин x и y (не может быть отрицательного числа пирожков и пирожных). В итоге мы получили систему неравенств:

x + 4y 1000, x + y 700, x 0, y 0 ()

Формализуем стратегическую цель: получение максимальной выручки. Выручка — это стоимость всей проданной продукции. Пусть цена одного пирожка r рублей. По условию задачи, цена пирожного в два раза больше, т.е. 2r рублей. Отсюда стоимость всей произведенной за день продукции равна rx + 2ry = r(x + 2y). Целью производства является получение максимальной выручки. Будем рассматривать записанное выражение как функцию от x, y: F(x, y) = r(x + 2y). Поскольку r — константа, то максимальное значение F(x, y) будет достигнуто при максимальной величине выражения x + 2y. Поэтому в качестве функции, максимум которой соответствует стратегической цели, можно принять

f(x, y) = x + 2y ()

Следовательно, получение оптимального плана свелось к следующей математической задаче: найти значения плановых показателей x и y, удовлетворяющих системе неравенств () и придающих максимальное значение целевой функции ().

Методические рекомендации

Приведенный выше пример относится к классу задач линейного программирования. В теории оптимального планирования существует несколько классов задач, из которых линейное программирование — самый простой вариант. Изучение математических методов решения таких задач выходит за рамки целей школьного образования.

Вместе с тем было бы не логично ограничиться лишь теоретической постановкой задач оптимального планирования. Современные информационные технологии позволяют решать некоторые задачи оптимального планирования (и, в частности, линейного программирования) без проникновения в существо применяемых математических методов. В частности, такие средства имеются в табличном процессоре Excel, и на их основе можно продемонстрировать ученикам приемы решения конкретных задач. Средство, о котором идет речь, называется Поиск решения. Соответствующая команда находится в меню Сервис. Опишем кратко, как воспользоваться указанным средством для решения поставленной выше задачи.

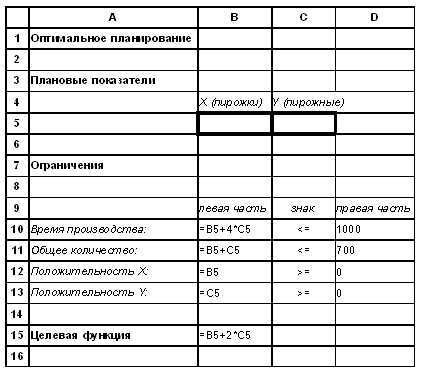
Вначале подготовим таблицу к решению задачи оптимального планирования.

Ячейки B5 и C5 зарезервированы, соответственно, для значений x (план по изготовлению пирожков) и y (план по изготовлению пирожных). Левые части неравенств в столбце В, правые — в столбце D; знаки “ =D12; B13>=D13. Ограничения вводятся следующим образом:

· щелкнуть по кнопке “Добавить”;

· в появившемся диалоговом окне “Добавление ограничения” вводим ссылку на ячейку В10, выбираем из меню знак неравенства “ Зависимость скорости падения от времени с учетом сопротивления воздуха

Заметим, что установившееся предельное значение скорости можно вычислить аналитически, не прибегая к численным методам. Приравняв в формуле (6) dv/dt (ускорение) к нулю, получим, что установившаяся скорость будет равна

и далее не будет возрастать.

На основании данной модели можно, например, решать задачу оптимизации, сформулировав условие так: парашютист прыгает с некоторой высоты и летит, не открывая парашюта; на какой высоте (или через какое время) ему следует открыть парашют, чтобы иметь к моменту приземления безопасную скорость? Другая задача: как связана высота прыжка с площадью поперечного сечения парашюта (входящей в k₂), чтобы скорость приземления была безопасной?

Существенной проблемой при использовании описанного численного метода является выбор величины шага по времени t. От этой величины зависит точность получаемых результатов, устойчивость вычислительной процедуры. Все эти проблемы исследуются в математической дисциплине, которая называется “Численные методы”, или “Вычислительная математика”.

Методические рекомендации

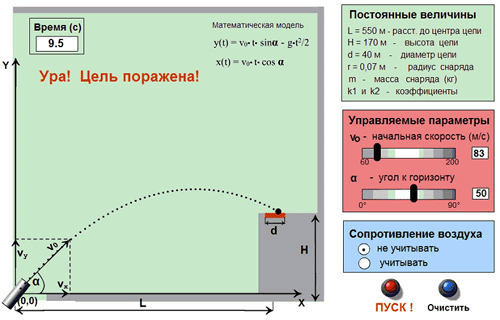
Знакомство учащихся с компьютерными моделями физических процессов в базовом курсе информатики может происходить на уровне демонстрационных примеров. На рисунке показан пример учебной демонстрационной программы, моделирующей полет снаряда, выпущенного из пушки. Задача, которая ставится перед учениками, заключается в подборе параметров (начальной скорости и угла выстрела), которые обеспечивают попадание снаряда в цель (данная программа включена в федеральную коллекцию цифровых образовательных ресурсов). Аналогичные разработки имеются и в других учебных источниках.

Полет снаряда, выпущенного из пушки

В старших классах физико-математического профиля вопросы моделирования физических процессов должны входить в программу профильной подготовки. Можно предложить следующий перечень объектов моделирования, связанных с движением тел:

· движение тел с учетом сопротивления среды (свободное падение, движение тела, брошенного под углом к горизонту, взлет ракеты и др.);

· колебательное движение маятника с учетом сопротивления среды, вынужденные колебания, резонанс и т.д.;

· движение небесных тел (задача двух тел);

· движение заряженных частиц в электрических полях.

Другие типы задач, на базе которых можно реализовывать моделирование физических процессов, связаны с описанием физических процессов в приближении сплошной среды и в электромагнитных полях:

· моделирование процесса теплопроводности и др.;

· моделирование распределений статических — электрического и магнитного — полей.

Выше был подробно разобран пример моделирования свободного падения тела в атмосфере, в котором используются дифференциальные уравнения и численные методы их решения. Если математической подготовки учеников недостаточно для понимания такого подхода, то можно построить математическую модель сразу в конечно-разностной форме, не используя дифференциальных уравнений. Продемонстрируем методику применения такого подхода.

Напомним ученикам, что ускорение есть приращение скорости за единицу времени, а скорость — приращение перемещения за единицу времени: .

Знаки приближенного равенства свидетельствуют о том, что эти соотношения тем точнее, чем меньше промежуток t; в пределе t 0 они становятся точными.

Если в некоторый момент времени t₀ величина s имеет значение s(t₀), а величина v — значение v(t₀), то в последующий момент времени t₁ = t₀ + t будем иметь:

При этом предполагается, что ускорение в течение данного отрезка времени не изменялось и оставалось равным a(t₀). Здесь также использованы обозначения F₀ = F(t₀), m = m(t₀), т.е. имеется в виду, что сила и масса в общем случае могут быть переменными величинами.

При вычислениях значений v и s в последующие моменты времени можно поступать аналогично. Если известны значения v_i и s_i в момент t_i, то

Таким образом, получены те же самые формулы метода Эйлера, но методически иначе. При этом вообще не упоминаются дифференциальные уравнения.

При построении этой и подобной ей моделей следует обратить внимание учащихся на то, что в разбиении непрерывного времени на отрезки длиной t проявляется одна из фундаментальных идей информатики об универсальности дискретной формы представления информации, отраженная как в конструкции компьютера, так и во множестве приложений информатики.

Отметим, что существует немало компьютерных программ, моделирующих простые физические процессы. В них реализован диалоговый интерфейс, позволяющий вводить параметры, получать на экране таблицы, графики, движущиеся изображения. Однако при их использовании остаются скрытыми физические законы, определяющие процесс, ограничения модели, возможности ее усовершенствования. Такие программы полезны скорее как иллюстративные, ознакомительные. Учащихся, изучающих информатику на профильном уровне, целесообразно ориентировать на подробный анализ математических моделей и самостоятельную разработку программ.

Источник