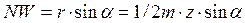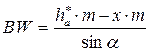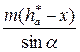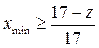Интерференция зубьев на шестерне что это

2.7. ИНТЕРФЕРЕНЦИЯ ЗУБЧАТЫХ КОЛЕС

Интерференция профилей приводит к заклиниванию зубьев одного колеса во впадинах другого. Для исключения интерференции в эвольвентном зацеплении точки касания профилей зубьев колес должны всегда находиться на линии зацепления, что обеспечивается при угле профиля α = 20° числом зубьев колес больше 17.

При нарезании эвольвентных зубчатых колес с числами зубьев меньше 17 имеет место интерференция части профиля зуба колеса и профилей зубьев режущего инструмента. В этом случае режущие кромки инструмента срезают часть формообразующей кривой профилей зубьев колеса.

При положительных значениях коэффициента относительного смещения имеет место интерференция профилей зубьев режущего инструмента и части эвольвентного профиля, принадлежащего головке зуба колеса, что приводит к срезу этой части профиля. В этом случае имеет место заострение зуба колеса (рис.8).

Изменение профилей зубьев колес приводит к увеличению нагрузочной способности механизма. Заострение головок зубьев зубчатых колес является нежелательным, т. к. это приводит к снижению кинематической точности механизма и вызывает увеличение склонности зубьев к скалыванию.

Рисунок 8. Заострение зуба колеса.

Зуб зубчатого колеса считается незаостренным, а зубчатый механизм − сохраняющим работоспособность при выполнении следующего условия:

где [sa ] − допускаемое значение толщины зуба по окружности вершин sa:

При отрицательных значениях коэффициента относительного смещения относительного, имеет место интерференция профилей зубьев режущего инструмента и части эвольвентного профиля, принадлежащего ножке зуба колеса, что приводит к срезу этой части профиля. В этом случае имеет место подрезание части профиля зуба колеса в его основании в области переходной кривой (рис. 9).

Изменение профилей зубьев колес приводит к увеличению кинематической точности механизма. Подрезание ножек зубьев зубчатых колес является нежелательным, т. к. это ослабляет ножку зуба колеса, что приводит к уменьшению нагрузочной способности механизма.

Зуб зубчатого колеса считается не подрезанным, а зубчатый механизм − сохраняющим работоспособность при выполнении следующего условия:

Минимальное значение коэффициента относительного смещения, при котором обеспечивается отсутствие подреза ножек и заострение головок зубьев зубчатых колес, определяется по выражению

Источник

Подрезание – наложение профиля зуба инструмента на профиль зуба изготавливаемого колеса при нарезании зубьев.

Заклинивание – наложение профилей зубьев, но не при изготовлении, а при зацеплении колес.

Рассмотрим подробней явление подрезания. Так как параметры зуборезного инструмента стандартны, то при прочих равных условиях возможность подрезания ножки зуба определяется положением точки N, т.е. размерами колеса. Подрезание не происходит, когда точка контакта между производящей поверхностью инструмента и профилем зуба нарезаемого колеса находится правее точки N. Левее точки N эти поверхности будут не касаться друг друга, а пересекаться, что и приводит к подрезанию ножки зуба. Подрезание уменьшает эвольвентную часть профиля зуба колеса, ослабляет прочность зуба в опасном сечении и уменьшает коэффициент перекрытия.

Рассмотрим вопрос о наименьшем числе зубьев Z_min на колесе, при котором явление подрезания будут отсутствовать при нарезании зубьев рейкой с учетом смещения.

По условию не подрезания, должно выполняться условие NW ≥ BW. Из треугольника ОNW можно выразить катет NW, используя модуль и число зубьев

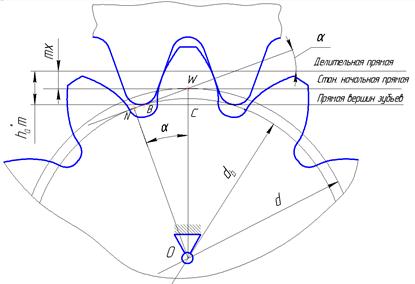
Из треугольника BWC можно найти гипотенузу BW, используя модуль,

высоту головки зуба и коэффициент смещения Рисунок 5 инструмента

≥

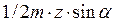
Отсюда число зубьев, которое можно нарезать реечным инструментом без подрезания ножки зуба, с учётом смещения будет равно

= (3)

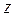
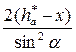
Минимальное число зубьев без смещения реечного инструмента и без подрезания ножки зуба, можно нарезать

==17,01 (4)

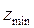
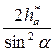
Используя выражение (3) и (4), можно определить минимальный коэффициент смещения, при котором не будет подрезания ножки зуба.

Смещение зуборезного инструмента меняет не только параметры зубчатых колес, но и зацепления в целом, поэтому при исправлении смещением, рассматривается суммарный коэффициент смещения (х_å).

В последних двух случаях такое исправление называется угловым.

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник

2.7. ИНТЕРФЕРЕНЦИЯ ЗУБЧАТЫХ КОЛЕС

Интерференция профилей приводит к заклиниванию зубьев одного колеса во впадинах другого. Для исключения интерференции в эвольвентном зацеплении точки касания профилей зубьев колес должны всегда находиться на линии зацепления, что обеспечивается при угле профиля α = 20° числом зубьев колес больше 17.

При нарезании эвольвентных зубчатых колес с числами зубьев меньше 17 имеет место интерференция части профиля зуба колеса и профилей зубьев режущего инструмента. В этом случае режущие кромки инструмента срезают часть формообразующей кривой профилей зубьев колеса.

При положительных значениях коэффициента относительного смещения имеет место интерференция профилей зубьев режущего инструмента и части эвольвентного профиля, принадлежащего головке зуба колеса, что приводит к срезу этой части профиля. В этом случае имеет место заострение зуба колеса (рис.8).

Изменение профилей зубьев колес приводит к увеличению нагрузочной способности механизма. Заострение головок зубьев зубчатых колес является нежелательным, т. к. это приводит к снижению кинематической точности механизма и вызывает увеличение склонности зубьев к скалыванию.

Рисунок 8. Заострение зуба колеса.

Зуб зубчатого колеса считается незаостренным, а зубчатый механизм − сохраняющим работоспособность при выполнении следующего условия:

где [sa ] − допускаемое значение толщины зуба по окружности вершин sa:

При отрицательных значениях коэффициента относительного смещения относительного, имеет место интерференция профилей зубьев режущего инструмента и части эвольвентного профиля, принадлежащего ножке зуба колеса, что приводит к срезу этой части профиля. В этом случае имеет место подрезание части профиля зуба колеса в его основании в области переходной кривой (рис. 9).

Изменение профилей зубьев колес приводит к увеличению кинематической точности механизма. Подрезание ножек зубьев зубчатых колес является нежелательным, т. к. это ослабляет ножку зуба колеса, что приводит к уменьшению нагрузочной способности механизма.

Зуб зубчатого колеса считается не подрезанным, а зубчатый механизм − сохраняющим работоспособность при выполнении следующего условия:

Минимальное значение коэффициента относительного смещения, при котором обеспечивается отсутствие подреза ножек и заострение головок зубьев зубчатых колес, определяется по выражению

Рисунок 9. Подрезание зуба колеса.

3. ОПРЕДЕЛЕНИЕ РАЗМЕРОВ ЗУБЧАТОГО ЗАЦЕПЛЕНИЯ

Размеры колес, а также всего зацепления, зависят от чисел Z1 и Z2 зубьев колес, от модуля m зацепления (определяемого из расчета зуба колеса на прочность), общего для обоих колес, а также от метода их обработки.

Предположим, что колеса изготавливаются по методу обкатки инструментом реечного типа (инструментальной рейкой, червячной фрезой), который профилируется на основе исходного контура согласно ГОСТ 13755-81 (рис. 10).

Процесс изготовления зубчатого колеса (рис. 10) инструментальной рейкой по методу обкатки заключается в том, что рейка в движении по отношению к обрабатываемому колесу перекатывается без скольжения одной из своих делительных прямых (ДП) или средней прямой (СП) по делительной окружности колеса (движение обкатки) и одновременно совершает быстрые возвратно-поступательные перемещения вдоль оси колеса, снимая при этом стружку (рабочее движение).

Расстояние между средней прямой рейки (СП) и той делительной прямой (ДП), которая в процессе обкатки перекатывается по делительной окружности колеса, называется смещением Х рейки (см. п. 2.6). Очевидно, что смещение Х равно расстоянию, на которое отодвинута средняя прямая рейки от делительной окружности колеса. Смещение считается положительным, если средняя прямая отодвинута в направлении от центра нарезаемого колеса.

Величина смещения Х определяется формулой:

где х – коэффициент смещения, который имеет положительное или отрицательное значение (см. п. 2.6).

Рисунок 10. Станочное зацепление.

Зубчатые колеса, изготовленные без смещения инструментальной рейки, называются нулевыми; изготовленные при положительном смещении рейки – положительными, при отрицательном смещении – отрицательными.

В зависимости от значений х_Σ зубчатые зацепления классифицируются следующим образом:

а)если х_Σ = 0, при чем х1 = х2 = 0, то зацепление называется нормальным (нулевым);

в)если х_Σ ≠ 0, то зацепление называется неравносмещенным, при чем при х Σ > 0 зацепление называется положительным неравносмещенным, а при х Σ

Применение нормальных зубчатых колес с постоянной высотой головки зубьев и постоянным углом зацепления, вызвано стремлением получить систему сменных зубчатых колес с постоянным расстоянием между центрами для одной и той же суммы чисел зубьев, с одной стороны, и с другой стороны – сократить число комплектов зуборезного инструмента в виде модульных фрез, которыми снабжаются инструментальные мастерские. Однако условие сменности зубчатых колес при постоянном расстоянии между центрами может быть удовлетворено и при применении косозубых колес, а также колесами, нарезанными со смещением инструмента. Наибольшее применение нормальные зубчатые колеса находят в передачах при значительных числах зубьев обоих колес (при Z₁ > 30), когда эффективность применения смещения инструмента значительно меньше.

При равносмещенном зацеплении ( х Σ = х₁ + х₂ = 0) толщина зуба (S₁) по делительной окружности шестерни увеличивается за счет уменьшения толщины зуба (S₂) колеса, но сумма толщин по делительной окружности сцепляющихся зубьев остается постоянной и равной шагу. Таким образом, нет необходимости в раздвигании осей колес; начальные окружности так же, как и у нормальных колес, совпадают с делительными; угол зацепления не изменяется, но меняется соотношение высот головок и ножек зубьев. В связи с тем, что прочность зубьев колеса понижается, такое зацепление может применяться только при малых числах зубьев шестерни и значительных передаточных отношениях.

При неравносмещенном зацеплении ( х Σ = х₁ + х₂ ≠ 0) сумма толщин зубьев по делительным окружностям обычно больше, чем у нулевых колес. Поэтому оси колес приходится раздвигать, начальные окружности не совпадают с делительными и угол зацепления увеличен. Неравносмещенное зацепление имеет большие возможности, чем равносмещенное, и поэтому имеет более широкое распространение.

Применяя смещение инструмента при нарезании зубчатых колес можно повысить качество зубчатого зацепления:

а) устранить подрезание зубьев шестерни при малом числе зубьев;

б) повысить прочность зубьев на изгиб (до 100 %);

в) повысить контактную прочность зубьев (до 20 %);

г) повысить износостойкость зубьев и др.

Но следует иметь в виду, что улучшение одних показателей ведет к ухудшению других.

Существуют простые системы, которые позволяют определить смещение по простейшим эмпирическим формулам. Эти системы повышают показатели работы передач по сравнению с нулевыми, однако они не используют все возможности смещения.

В соответствии с рекомендациями ISO предложены следующие правила выбора коэффициентов смещения:

а) при числе зубьев шестерни Z₁ ≥ 30 применяют нормальные колеса;

Суммарное смещение ограничивается величиной:

в) при числе зубьев шестерни Z₁ суммарном числе зубьев Z₁ + Z₂

Суммарное смещение ограничивается величиной:

х Σ ≤ 1,8 – 0,03 · (Z₁ + Z₂), если 30 х Σ является максимально возможной при выполнении следующих требований:

а) не должно быть подрезания зубьев при обработке их инструментальной рейкой;

б) предельно допустимая толщина зуба по окружности выступов принята 0,3m;

в) наименьшее значение коэффициента перекрытия ε_α = 1,1;

г) обеспечение наибольшей контактной прочности;

д) обеспечение наибольшей прочности на изгиб и равнопрочности (равенства напряжений изгиба) зубьев шестерни и колеса, изготовленных из одинакового материала с учетом разного направления сил трения на зубьях;

е) наибольшей износостойкости и наибольшего сопротивления заданного (равенство удельных скольжений в крайних точках зацепления).

Данными таблицами нужно пользоваться следующим образом:

а) для неравномерного внешнего зацепления коэффициенты смещения х1 и х2 определяются в зависимости от передаточного отношения

i_1,2: при 2 ≥ i_1,2 ≥ 1 по табл. 1; при 5 ≥ i_1,2 > 2 по табл. 2, 3 по заданным Z₁ и Z₂.

После определения коэффициентов смещения все размеры зацепления подсчитываются по формулам, приведенным в табл. 5.

Источник

Коническая передача

Наиболее известные виды конических зубчатых колес имеют угол наклона менее 90 градусов и, следовательно, имеют коническую форму. Этот тип конической шестерни называется внешней, потому что зубья шестерни направлены наружу. Шаговые поверхности зацепленных наружных конических зубчатых колес соосны с валами зубчатых колес; вершины двух поверхностей находятся в точке пересечения осей валов.

Использование подлинной конической передачи имеет даже большее значение для надежности оси, чем любая другая запчасть. Конические шестерни с углом наклона более девяноста градусов имеют зубья, обращенные внутрь, и называются внутренними коническими шестернями.

Торцевые шестерни представляют собой сопрягаемые конические шестерни с одинаковым количеством зубьев и осями, расположенными под прямым углом.

Конические шестерни классифицируются на разные типы в зависимости от геометрии:

Источник

Зубчатое колесо

Зубчатые передачи весьма широко и продуктивно применяются в конструкциях современных машин, механизмов и устройств. Транспортные средства, энергетические установки, грузоподъемные устройства, авиационные установки, сельскохозяйственные машины, точные приборы — во всех них найдутся те или иные варианты зубчатого колеса. В технике зубчатая передача используется с целью распространения вращательного движения между осями валов, которые могут быть расположены параллельно, скрещиваться или пересекаться. Также, при помощи подобной передачи легко преобразовать вращательное движение, например, в поступательное, или реализовать эффективное преобразование крутящего момента и оборотов валов. Благодаря последнему свойству их используют в редукторах или мультипликаторах различных типов, а также коробках передач.

Основными преимуществами подобного способа передачи мощностей являются высокий КПД; компактный конструктив; плавная работа; точность; долговечность; надежность; возможность осуществления передачи силы с использованием любого угла, передаточного числа (до нескольких тысяч) и большого диапазона скоростей (до 150 м/с). Эти качества и обусловили распространение использования зубчатых передач в технике. К негативным моментам можно отнести технологическую сложность производства; требовательность к точности обработки, материалам и обрабатывающему оборудованию. Выбор материала для зубчатого колеса один из наиболее важных критериев надежности и долговечности в дальнейшей его работе. Жесткость конструкции, обеспечивающая передаче высокую эффективность, к сожалению, не позволяет ей держать высокие значения динамических нагрузок, часто являющихся причиной разрушения механизма. В дополнение, этим передачам характерна повышенная шумность, снижения которой можно достичь повышением качества и точности при производстве изделий.

Что такое зубчатые колеса

В общем случае, шестерня, или зубчатое колесо — главная деталь одноименной передачи, имеет вид диска с расположенными на цилиндрической или конической поверхности зубьями. При помощи этих зубьев в процессе вращения происходит зацепление колес между собой, что позволяет реализовать перенос вращательного момента от одного вала, на котором расположено колесо, к другому. Зуб зубчатого колеса при вращении толкает зуб другого, сопряженного с ним, колеса, которое вследствие этого тоже начинает совершать вращательное движение.

Сопряженная зубчатая передача должна всегда состоять из двух типов элементов: ведущих и ведомых. При этом ведущим, по определению, называют колесо передающее (сообщающее) вращение, ведомым — то зубчатое колесо, которое имеет большой диаметр с большим количеством зубьев и приводит во вращение. В большинстве случаев используется пара зубчатых колес, одно из которых с большим числом зубьев, а другое с меньшим. Иногда элемент, несущий меньше зубьев, считается шестерней, тогда колесом считают тот, у которого зубьев больше.

Виды зубчатых колес

Все зубчатые колеса, виды которых также многочисленны, как и варианты их применения, делятся на основные типы по расположению осей валов и геометрии формы зубьев. Выделяют цилиндрические, конические, червячные, винтовые передачи. На практике, исходя из формы профиля зубьев, выделяют эвольвентные и круговые колеса, а по расположению — прямозубые и косозубые типы зубчатых колес.

Для параллельного случая расположения осей валов применяют цилиндрические передачи:

Конические передачи подходят для пересекающихся осей:

Когда оси перекрещиваются, тогда используют передачи:

Наибольшую распространенность среди машин и механизмов обрели цилиндрические зубчатые колеса. Им свойственна простота изготовления, надежность, малые габариты. Конические, червячные и винтовые виды зубчатых колес используют лишь тогда, когда компоновка машины предъявляет особые условия. Цилиндрические зубчатые передачи делятся на два существенных вида: внешнего и внутреннего зацепления. В первом варианте реализации колесо и шестерня, у которой внешнее зацепление, крутятся в направлениях, которые противоположны друг другу. Во втором — колесо внутреннего зацепления и шестерня внешнего зацепления совершают вращательное движение со направленно. Существует также реечная передача — в ней рейка с зубьями сопрягается с имеющей внешнее зацепление шестерней.

Косозубые цилиндрические колеса имеют расположенные под углом к оси зубья. Сопряженные колеса имеют одинаковый наклон зубьев, но различные его направления. У одного наклон будет правым, у другого же — левым. Наличие наклона дает возможность передавать большие, по сравнению с прямозубыми, нагрузки, способствует плавному зацеплению зубьев и снижению шума.

Шевронные колеса представляют собой пару соединенных колес с косыми зубьями, имеющими равный угол наклона, но расположенными противоположно: одно с правым, второе с левым наклоном. Это позволяет уравновесить осевые силы, тем самым снизив нагрузку на подшипник. Колеса могут иметь в середине канавку. Колеса без канавки более прочны, но сложны в изготовлении.

Винтовые цилиндрические передачи, в свою очередь, применяют для вращения валов, когда угол их перекрещивания лежит в пределах от 0 до 90 градусов. Они похожи на косозубые колеса, однако винтовая передача имеет контакт точечный, а не линейный, как косозубая. Направление наклона зубьев у всех таких сопряженных колес одинаковое. Точечный контакт зубов вызывает повышение их износа, как следствие их используют только на небольших нагрузках.

Реечные передачи составляются из зубчатых колес и реек, которые также имеют зубья. Вращаясь, цилиндрическое колесо, перемещает сопряженную рейку по перпендикулярной оси колеса прямой. Таким способом движение из вращательного превращается в поступательное. Подобная передача бывает как с косыми зубьями, так и с прямыми.

Прямозубые конические колеса обладают зубьями, пересекающими оси этих колес. Коническое расположение позволяет вращать пересекающиеся или скрещивающиеся оси. Зубья также могут быть косыми, т.е. касательными к окружности. Угол наклона зубьев у таких колес составляет не больше тридцати градусов. Снабжение конических колес зубьями с нулевым углом наклона обеспечивает первым невысокие осевые и радиальные нагрузки, дает возможность применения подшипников скольжения. Эти качества делают передачи с использованием таких колес компактными, а изготовление не затратным.

Использование криволинейных зубьев для применения в конических зубчатых колесах резко снижает шумность передач и повышает прочность. Конические передачи подобного рода всегда имеют в зацеплении как минимум два зуба, что дает им возможность выдерживать нагрузку, которая выше на 30% относительно идентичных прямозубых и колес, имеющих нулевой наклон.

Гипоидные зубчатые колеса подобны коническим, но ось ведущей шестерни у них смещена выше или ниже относительно оси колеса, которое она ведет. У таких передач шестерни имеют наклон зубьев больший, чем у колес. Нормальный шаг при этом у шестерни и зубчатого колеса будет одинаковый, а торцовый — у шестерни больше. Гипоидной передаче не присуще чистое качение или скольжение, все ее точки подвержены скольжению. Это придает ей плавность и повышенную бесшумность. Кроме того, притирка происходит быстрее и качественней. Минус — присутствие скольжения вызывает повышенный износ поверхности зубов, что требует применения для таких передач специализированных масел.

Червячные передачи цилиндрические имеют червяк, имеющий геометрию цилиндра, на котором нарезаются витки, идущие вдоль направления винтовой линии. Червячное колесо должно иметь вогнутые зубья. Линейный контакт таких зубьев обеспечивает передачу больших нагрузок. Скольжение у червячных значительно выше, чем у прочих зубчатых передач. В глобоидной передаче червяк обладает вогнутой формой. Эта особенность позволяет участвовать в процессе зацепления большему числу зубьев, что повышает величину передаваемых такой передачей нагрузок.

Спироидные передачи занимают промежуточное место между червячными и гипоидными вариантами. В отличие от червячной, у гипоидной передачи червяк имеет форму конуса и зацепляется с колесом, на котором зубья располагаются на торцевой стороне.

Конструкция зубчатого колеса

Металлические зубчатые колеса, чертеж которых иногда довольно сложен, имеют разнообразные варианты конструкций, однако в них можно выделить три основных компоненты: венец с зубьями, ступицу и сам колесный диск. Венец зубчатого колеса является основным компонентом и на него приходится основная нагрузка. Зубья имеют различную геометрию. Наружная часть у зуба — это вершина, прилегающие к ней боковые части — головка зуба. Внутренняя часть зуба называется его ножкой. Пространство между двумя ближними ножками образует впадину колеса. Чтобы крепить шестерню или колесо на валу, в центре диска располагается ступица, имеющая сквозное отверстие, форма которого напрямую зависит от сечения вала: она может иметь форму цилиндра, квадрата или любого другого многоугольника. В случае цилиндрических валов, ступица часто имеет т.н. шпоночный паз. В целях экономии материалов и веса колеса, его диск имеет толщину, меньшую по сравнению с толщиной обода и ступицы. Часто в диске для этих целей еще выполняют различные отверстия.

Основные параметры

Чтобы обеспечивать возможность конструирования работоспособных зубчатых передач, размеры колес и шестерен, а также их прочностные и массогабаритные характеристики описываются специальными параметрами, величины которых хорошо стандартизированы ГОСТ. Так, эвольвентный профиль, положенный в основу сечения зуба подавляющего большинства колес, характеризуется модулем зацепления и имеющимся количеством зубьев на колесе или шестерне. Довольно часто, эвольвентные зубчатые колеса, имея один и тот же диаметр, могут иметь существенно различающие значения данных величин. Окружной модуль, служащий основной характеристикой для зубьев, по стандарту может иметь значения в диапазоне от 0,05 до 100 мм. Главными параметрами геометрии у различных зубчатых колес являются следующие диаметры: начальный, основной и делительный. Шагом зубчатого колеса называется общее расстояние ширины зуба и впадины. Так же важным параметром является радиус колеса. Радиуса зубчатых колес делятся: радиус окружности вершин, радиус делительной окружности, радиус основной окружности, радиус окружности впадин.

Диаметры окружностей

Зубчатое колесо описывается несколькими окружностями, являющимися важными характеристиками их геометрии. Так, диаметр вершин дает максимальные размеры зубчатого колеса. Ему противоположен диаметр окружности впадин. Высчитав разность между этими двумя величинами и разделив ее пополам, получим полную длину зуба. Важным параметром считается диаметр делительной окружности, имеющий формулу d=pz/3,14, по нему можно определить окружной шаг p расположенных на колесе зубьев, иначе называемый шагом зацепления, имеющий геометрический смысл части длины этой окружности, приходящейся на каждый зуб. В общем случае, диаметр делительной окружности отделяет высоту головок и высоту ножек зуба. Он также задает кривую, являющуюся необходимой базой для построения самой эвольвенты, и используется для построения требуемого в конкретной задаче профиля зубьев колес и шестерен.

Модули зубчатых колес

Чтобы упростить расчеты элементов, использующихся для зацепления, для зубчатых колес была введена стандартизованная ГОСТ величина, названная модулем. Модуль зубчатого колеса является частью от диаметра имеющейся делительной окружности зубчатого колеса, которая приходится на зуб: m=d/z. Таким образом, количество зубьев колеса, его собственный делительный диаметр и его модуль — во взаимовлиянии. Модуль можно расписать как отношение шага зацепления колеса и числа Пи: m=d/3,14. Когда передаваемая зубчатыми колесами нагрузка невелика, то лучше использовать малые модули. Малый модуль дает более длительный срок эксплуатации и упрощается обработка зубчатых колес. В данном случае на делительном диаметре разместится больше зубьев, а значит и зацепление будет происходить с большим их числом, что уменьшит нагрузку на отдельные зубья шестерен. У прямозубых цилиндрических колес бывает всего только один модуль, у косозубых — два: нормальный и окружной. В расчетах используют первый.

Расчет параметров

Для всех зубчатых колес инженерный расчет их параметров является задачей комплексной, в ходе решения которой принимается во внимание конструкция всей передачи. Вначале нужно определиться с числом зубьев и необходимым в задаче модулем зацепления. Для выбора последнего необходимы параметры прочности и предполагаемого срока службы колес; материала, из которого оно будет изготовлено. На основе этих данных рассчитывается минимально возможная в данной задаче величина модуля зацепления, которое затем приводится к стандартизованным значениям, находящимся из соответствующих таблиц. Передаточное отношение высчитывается с применением формулы u=z₂z₁, где z₂ — это количество колесных зубьев, а z₁ — количество зубьев, находящихся на шестерне. Оно позволяет понять, сколько всего нужно зубьев на колесах, подлежащих сопряжению. Зная модули и полученное число зубьев для всех колес и шестерней, можно произвести дальнейшие расчеты размеров требуемых деталей, используя стандартный метод для их расчетов.

Применение

Каждый из видов передач имеет свои преимущества и отрицательные качества. Нарезание прямозубых колес — довольно простой технологический процесс, поэтому они широко применяются в промышленности. Косозубые, как и прямозубые цилиндрические колеса, используются в тракторах, станках, коробках передач автотранспорта. Цилиндрические колеса с использованием внутреннего зацепления, благодаря компактности и прочности, нашли себя в самолетах, трансмиссиях автомобилей, редукторах, в шлицевых соединениях и сложных планетарных передачах, которые славятся своим особенно малым весом и габаритными размерами. При этом они предоставляют высокие передаточные числа и значительно сниженные уровни шумов при своей работе. Шевронные колеса, будучи трудоемкими в производстве, используются в больших редукторах и их ремонте, где требуется плавная и бесшумная передача значительных нагрузок. Конические колеса с нулевым наклоном и их прямозубые аналоги, имея высокую компактность и невысокую себестоимость изготовления, эксплуатируются в дифференциалах автомашин и станков. Криволинейные зубья обеспечивают коническим колесам особую прочность и малошумность, поэтому их можно найти в ответственных и скоростных передачах. Их используют практически везде: от самолетов до тракторов. Гипоидные зубчатые пары можно делать с большим передаточными числами (до 100:1), они часто используются в металлорежущем оборудовании.

Зубчатое колесо и шестерня — отличия

Главными деталями в зубчатой передаче – зубчатое колесо и шестерня. Они применяются во многих промышленных узлах, машинах. Многие полагают, что зубчатое колесо и шестерня это одна и та же деталь и у них нет различий между собой. Специалисты, которые тесно связаны с промышленностью и машиностроением так не считают и уверяю, что это разные детали хоть и выполняют по сути одну и ту же функцию передачу вращательного движения. Давайте разберем основные моменты по данному вопросу.

Особенности зубчатых колес и шестерней

Внешне зубчатое колесо и шестерня имеют схожесть в виде диска с расположенными на нем зубцами. Их расположение может быть как на конической, так и цилиндрической поверхности. Основной задачей данных деталей является передача крутящего момента. Для того чтобы получить и передать крутящий момент, нужна ответная шестерня, то есть пара. Мы разобрали выше, что существует ведомая деталь и ведущая. С ведущей начинается движение и дальнейшая передача крутящего момента на ведомую деталь. В этом ключевом моменте и есть отличие зубчатого колеса от шестерни, ведущая деталь является шестерней, а ведомая зубчатым колесом. Получается, что вся разница между ними в том какую роль в механизме выполняет деталь.

Отметим что при работе двух зубчатых колес, колесо, которое имеет большее количество зубьев, называют шестерней. В ГОСТ 16530-83 есть пояснение, что зубчатое колесо и шестерня являются словами синонимами, шестерня является главным и ведущим зубчатым колесом. Существуют специалисты работающие в определенных областях промышленности и машиностроения, которые четко разделяют разницу между зубчатым колесом и шестерней. Они убеждены, что изготовление зубчатых колес это одно, а производство шестерней это другое, так как между ними есть различия.

Почему вам стоит обращаться в нашу компанию

Наша компания работает на своих станочных мощностях, что позволяет выполнять работы не только быстрее посредников, но и с более выгодными условиями на изготовление червячных зубчатых колес.

Работаем с любыми видами стали:

Мы оказываем полный спектр услуг по металлообработке на современном, точном оборудовании с помощью качественного режущего инструмента, что позволяет нашим специалистам получать максимальной точности детали с чертежом заказчика.

Источник