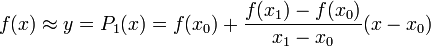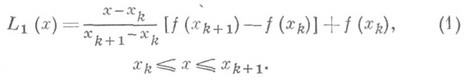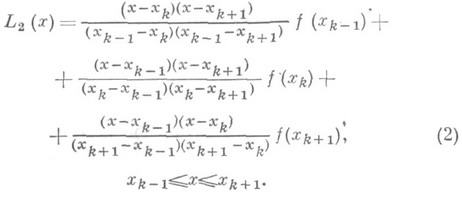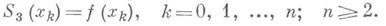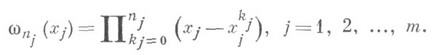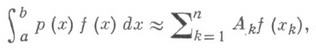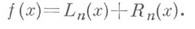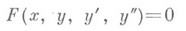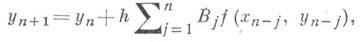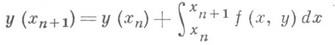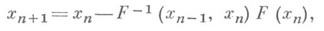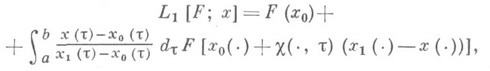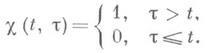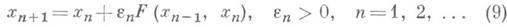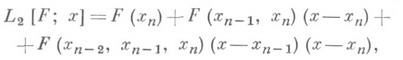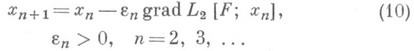Интерполировано что это в музыке

ru.knowledgr.com

Интерполяция (также известный, как переигрывается), особенно музыка 20-го века и позже, является резким изменением музыкальных элементов, с (почти немедленный) возобновление главной темы или идеи. Частями, которые процитированы в качестве показа интерполяции среди других методов, является Музыка для Медного Квинтета Гюнтера Шуллера и Погребального пения Жертвам Хиросимы Кшиштофом Пендерецким, оба 1960–61.

В классической музыке

Для музыки Классического периода интерполяция определена в контексте музыкального предложения или периода как, «несвязанный материал вставил между двумя логически последующими функциями».

Это устройство обычно используется, чтобы расширить то, что обычно было бы регулярной фразой в нерегулярную и расширенную фразу. Такое расширение интерполяцией достигнуто добавлением дополнительной музыки посреди фразы (обычно с помощью последовательности). Ясный пример существует во второй попытке Сонаты Фортепьяно Моцарта № 10, K.330.

Раньше, в спетых частях Массы, таких как входная или kyrie, это было допустимо, особенно во время средневекового периода, чтобы усилить литургическую формулу, интерполировав фарс (от Средневекового латинского farsa, фарша), также названный тропом. Это могло бы состоять из объяснительной фразы или стиха, обычно в форме дополнения или пересказа, часто в жаргоне.

В классическом наборе, состоя строго из аллеманды, куранты, сарабанды и gigue, композиторы часто интерполировали гавот, bourrée, менуэт, musette или паспье.

В популярной музыке

Интерполяция использовалась одним художником, чтобы относиться к добавлению нового материала в работе или записи ранее существующей музыкальной пьесы.

В музыке хип-хопа

В музыке хип-хопа интерполяция относится к использованию мелодии – или части мелодии (часто с измененной лирикой) – от ранее зарегистрированной песни, но перезаписи мелодии вместо того, чтобы пробовать его. Часто используемый, когда оригинальный художник или этикетка отказываются лицензировать фактический образец, так как перезаписи (покрытия) подвергаются обязательным лицензиям.

Пример: «Гетто, Supastar» Pras показывает крюк, спетый Mýa, который был первоначально написан в песне «Острова в Потоке» Кенни Роджерсом и Долли Партон.

Источник

Различные виды интерполяции. Воссоздание высоких частот

Примечание: сия статья ни в коем случае не является пособием для апконвертщиков (коим в аду специально уготовлено жаркое местечко) и опубликована лишь для общего развития; а также пущего понимания теории цифрового звука.

Виды интерполяции

Как известно, цифровой сигнал представляет собой набор отсчетов (семплов) с разным уровнем, которые следуют один за одним с определенной фиксированной (для привычной нам импульсно-кодовой модуляции) частотой. В определенных случаях частоту следования семплов (частоту дискретизации) может потребоваться изменить, т.е. может потребоваться т.н. ресемплинг. Ресемплинг условно можно разделить на два вида — с повышением частоты (апсемплинг) и понижением (даунсемплинг). И вот тут возникает вопрос: а каким же образом нам изменить количество семплов в потоке? Какие семплы отбросить, или же наоборот — как рассчитать уровень новых, промежуточных семплов?

Давайте для простоты ограничимся апсемплингом. Скажем, пускай нам надо повысить частоту дискретизации в два раза. Для этого надо удвоить количество семплов, т.е в промежутках между семплами вставить один дополнительный.

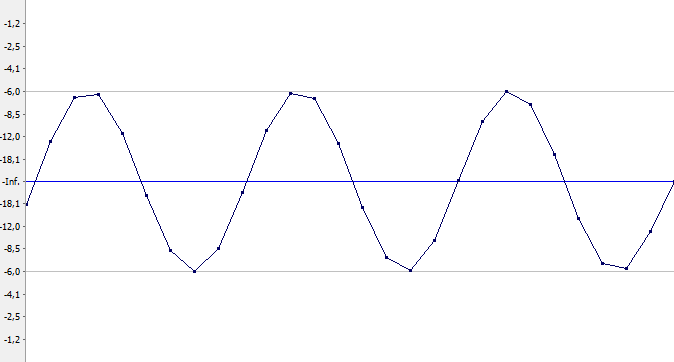
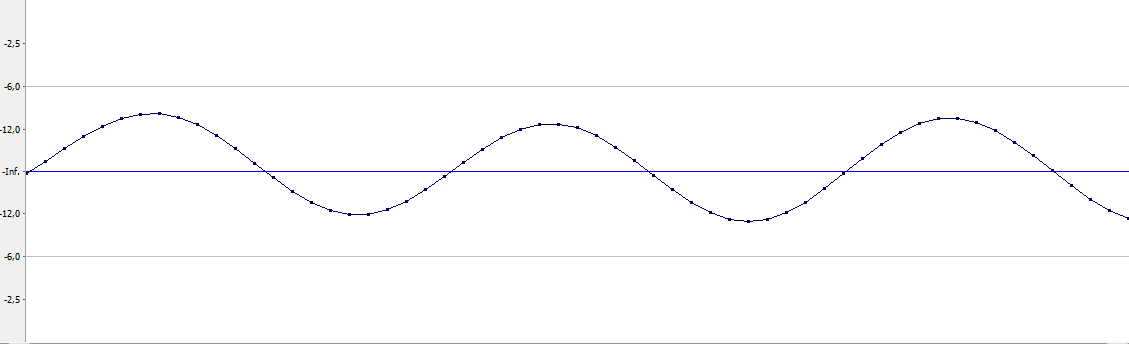
Рассмотрим вот такой сигнал:

Это три периода синусоидального сигнала с частотой 5000 Гц, оцифрованного с частотой дискретизации 44100 Гц (глубина квантования равна 32 битам, но для нас это не важно). Фактически смысл здесь имеют лишь точки (это и есть те самые семплы), линии между ними рисует программа Sound Forge. Как видим, на один период приходится примерно 9 семплов (441000/5000≈9). Нам надо увеличить это количество вдвое. Где же именно нам разместить промежуточные семплы?

Есть несколько способов расчета уровня промежуточных семплов (то есть интерполяции). Как я уже сказал, программа сама дорисовала линии, соединяющие соседние семплы. Эти линии — прямые, и если мы разместим промежуточный семпл (или семплы, если увеличиваем частоту более, чем в два раза) на этой линии, такой вид интерполяции будет называться линейной. Расчетную формулу для получения уровня промежуточного семпла можно найти из уравнения прямой. Уровень семпла x, находящегося между семплами x0 и x1 будет равен:

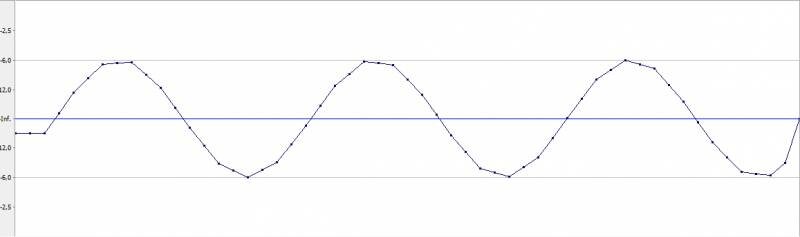
Результат преобразования частоты в 88.2 кГц будет следующим:

Собственно, отличий между двумя волнами вы не найдете, кроме количества семплов на период конечно.

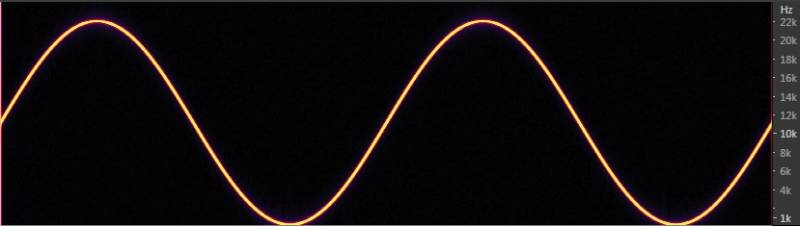
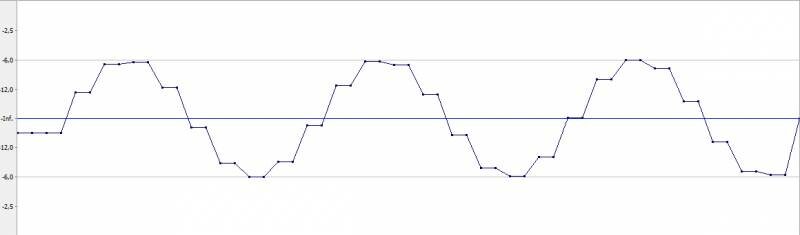
Теперь давайте возьмем сигнал с плавающей частотой (частота дискретизации 48 кГц) и сравним спектрограммы исходного и полученного после увеличения частоты дискретизации в два раза:

Мы видим, что в сигнале появились новые частотные составляющие: исходный спектр буквально отразился в высокочастотную область. Это явление называется алиазингом (alias — отражение). Кстати, надо отметить, что с понижением частоты сигнала уровень алиаса уменьшается. Это связано с уменьшением погрешности линейной интерполяции: при уменьшении разницы между уровнями соседних семплов (т.е. при уменьшении скорости нарастания сигнала, которая прямо пропорциональна частоте), ошибка квантования стремится к нулю.

Но есть еще более простой способ интерполяции, называемый интерполяцией нулевого порядка. Он даже не требует никаких расчетов: дополнительный семпл по уровню соответствует предыдущему.

Да, это те самые ступеньки, в виде которых непросвещенные люди так любят изображать цифровой сигнал. В случае со свип сигналом (плавающая частота) мы получим такую картинку:

Теперь мы получили точную копию исходного сигнала в области расширенного диапазона (отражение идет симметрично относительно исходной частоты Найквиста).

Надо отметить, что подобная картинка получается исключительно при кратном повышении частоты дискретизации (2x, 3x, 4x и т.д.). При дробном множителе мы получим сильные искажения во всем спектре частот.

Этот метод интерполяции активно используется в ЦАП (сигма-дельта ЦАП использует многократный ампсемплинг) — да, на определенном этапе оцифрованный сигнал действительно представляется в виде ступенек. Однако, после преобразования применяется фильтр низких частот, который фактически сглаживает сигнал.

На рисунке вы видите результирующий сигнал, полученный после фильтрации предыдущего, ступенчатого сигнала. Мы видим, что результирующая интерполяция получилась даже лучше линейной. Причиной этому является отсутствие дополнительных частотных составляющих, которые мы вырезали НЧ фильтром. Кстати говоря, убедиться, что в результате ЦА преобразования также не получается никаких ступенек, вы можете посмотрев это видео.

Именно так работают почти все ресемплеры: сначала количество семплов добивается до нужного путем копирования предыдущих, а затем полученный сигнал фильтруется примерно до исходной частоты Найквиста (чтобы отбросить отражение, т.е. алиазинг).

В зависимости от типа используемого НЧ фильтра и различают алгоритмы передискретизации. Наиболее популярным является sinc интерполяция с использованием sinc фильтра.

Более подробно о передискретизации можно почитать в статье Конвертеры частоты дискретизации. Мы же перейдем к одному интересному применению интерполяции нулевого порядка.

Воссоздание высоких частот

Для данного опыта нам понадобятся: foobar2000, ресемплеры, SSRC X, SoX, Secret Rabbit Code, а также SoX Lowpass filter. Всё это можно скачать на странице foobar2000 + плагины.

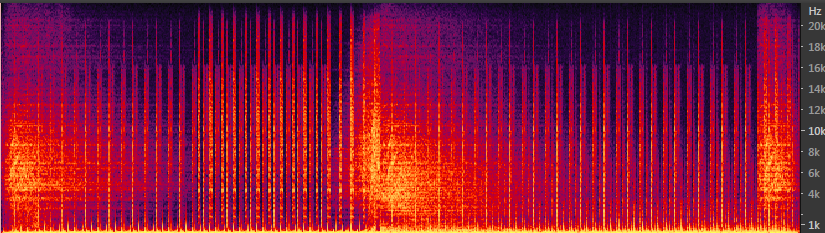
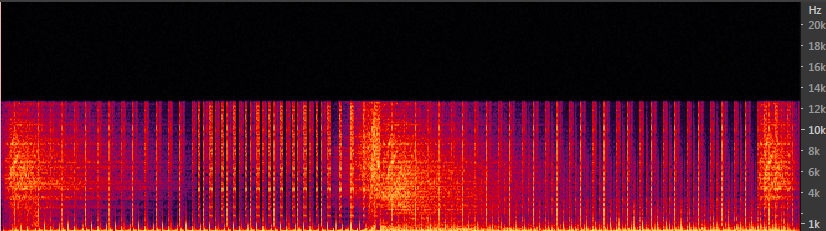
В качестве подопытного возьмем семпл из трека «Armin van Buuren — Sail». Семпл имеет широкий частотный диапазон:

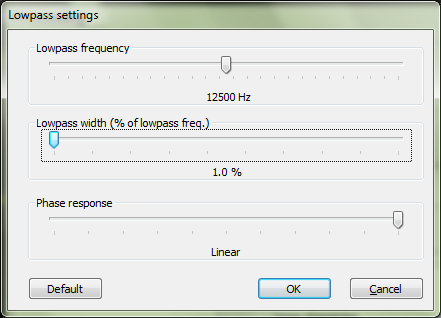
Теперь урежем частотный диапазон с помощью DSP Lowpass (SoX) до 12.5 кГц. Вот спектр результирующего семпла:

Ну, проблему создали, теперь самое время её решать.

Фишка интерполяции нулевого порядка как раз в том, что она умеет отражать более низкие частоты в область более высоких. Таким образом мы можем восстановить некое подобие высоких частот, которые по уровню будут зависеть от более низких. Для этого надо выполнить следующее:

1. Определить частоту среза. В нашем случае это 12.5 кГц.
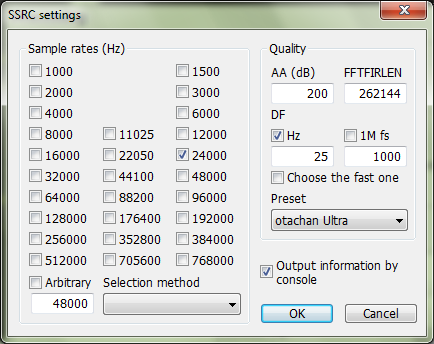
2. Выполнить ресемплирование до частоты приблизительно в два (но не более!) раза больше частоты среза. В данном случае нам идеально подойдет частота 24 кГц. Для ресемплирования воспользуемся SSRC X с максимальной полосой пропускания, которую обеспечивает пресет Otachan Ultra:

Это будет первое звено в цепочке DSP.

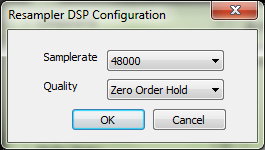
3. Теперь нам необходимо выполнить повышение частоты дискретизации ровно в два раза с использованием интерполяции нулевого порядка, и тем самым воссоздать частоты в диапазоне 12-24 кГц. Для этого добавим в цепочку Secret Rabbit Code Resampler с соответствующими настройками:

4. Выполнить ресемплирование до нужной частоты дискретизации. Это необходимо, например, если мы восстанавливали диапазон 8-16 кГц и результирующая частота дискретизации вышла 32 кГц, в то время как нам может понадобиться 44.1. Ресемплирования следует производить с помощью SoX Resampler. В нашем случае частота 48 кГц вполне приемлема.

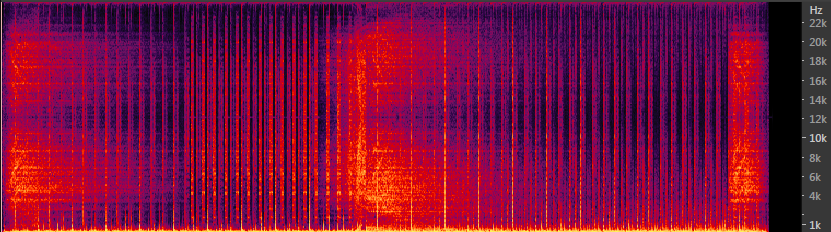
Вот, собственно, и всё. На выходе мы получаем сигнал с полным спектром:

В принципе, можно использовать и линейную интерполяцию. Тогда мы получим более естественную спектрограмму со спадом в области ВЧ:

Таким же образом можно воссоздать ВЧ при срезе на 16-17 кГц. Для этого выполняется даунсемплинг до 32 кГц, затем частота повышается с помощью интерполяции нулевого порядка (или линейной) до 64 кГц, после чего производится ресемплирование с помощью SoX до 44.1 кГц.

На этом всё. Надеюсь, вам было интересно. Удачи!

Информация от спонсора

Inksystem: системы непрерывной подачи чернил (СНПЧ). На этом сайте Вы можете ознакомиться с ассортиментом товаров компании: принтерами, МФУ, плоттерами, комплектующими и многим другим. Склады компании расположены в Минске, Санкт-Петербурге, Москве и Киеве. Постоянным клиентам предоставляются скидки.

Источник

Значение слова «интерполировать»

Источник (печатная версия): Словарь русского языка: В 4-х т. / РАН, Ин-т лингвистич. исследований; Под ред. А. П. Евгеньевой. — 4-е изд., стер. — М.: Рус. яз.; Полиграфресурсы, 1999; (электронная версия): Фундаментальная электронная библиотека

ИНТЕРПОЛИ’РОВАТЬ [тэ], рую, руешь, сов. и несов., что (науч.). Сделать (делать), произвести (производить) интерполяцию чего-н.

Источник: «Толковый словарь русского языка» под редакцией Д. Н. Ушакова (1935-1940); (электронная версия): Фундаментальная электронная библиотека

интерполи́ровать

1. филол. произвольно или случайно вставлять (вставить) в текст при переписке или в процессе редактирования

2. матем. находить (найти) промежуточные значения какой-либо величины по некоторым известным её значениям

Делаем Карту слов лучше вместе

Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать Карту слов. Я отлично умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!

Спасибо! Я обязательно научусь отличать широко распространённые слова от узкоспециальных.

Насколько понятно значение слова эклектизм (существительное):

Синонимы к слову «интерполировать&raquo

Предложения со словом «интерполировать&raquo

Понятия, связанные со словом «интерполировать»

Отправить комментарий

Дополнительно

Предложения со словом «интерполировать&raquo

Церковь определяла важнейшие события месяца, сезона, года, упорядочивая всё земное и мирское, интерполируя природные циклы в пространство литургического календаря.

Именно изучив – интерполировав мысли автора на события своей жизни и сделав выводы, корректировки и наметив новые планы.

Теперь науке осталось всего-навсего интерполировать этот успех и остановить прекрасное мгновенье не только для наблюдения, но и для живого участия, пребывания в нём.

Источник

ИНТЕРПОЛИРОВАНИЕ

Наибольшее значение в вычислительной математике имеет задача построения способов интерполирования функций. Интерполяция функционалов и операторов также широко используется при построении приближенных методов.

Обычно L_n(x)строится в виде

где _i(x)>- некоторая заранее выбранная система линейно независимых функций. Такое И. наз. линейным относительно системы _i(x)>, a L_n(x)- интерполяционным полиномом по системе

Алгебраическое И. более высокого порядка в задаче приближения функций на всем отрезке [ а, b]применяется на практике сравнительно редко. Обычно ограничиваются линейным И. по формуле (1) или квадратичным интерполированием с тремя узлами на частичных отрезках сетки по формуле

Имеются различные варианты записи алгебраич. интерполяционных многочленов (см. Интерполяционная формула).

Находит все большее применение И. сплайнами (см. Интерполяционный сплайн).

На практике чаще всего используются параболические или кубические сплайны. Интерполяционным кубическим сплайном дефекта 1 для функции f(x)относительно сетки D_n наз. функцию S₃(x)=S₃(f; х), являющуюся многочленом третьей степени на каждом из отрезков [x_k-1, x_k], принадлежащую классу дважды непрерывно-дифференцируемых функций и удовлетворяющую условиям

При таком определении имеется еще два свободных параметра, для нахождения к-рых налагаются дополнительные краевые условия:i=l,2;S’₃(a)= а _п и или нек-рые другие.

Как непосредственно для задачи приближения функций, так и при решении других задач используются сплайны, к-рые в точках сетки D_n совпадают не только со значениями функций f(x), но и со значениями производных этой функции до нек-рого порядка.

Часто при обработке эмпирических данных k> коэффициенты а _i в L_n(x)определяются, исходя из требования минимизации суммы

Такое построение функции L_n(x)наз. интерполированием по методу наименьших квадратов.

И. функций многих переменных имеет ряд принципиальных и вычислительных трудностей. Напр., в случае алгебраич. И. интерполяционный многочлен Лагранжа фиксированной степени, вообще говоря, не существует для произвольной системы различных узлов И. В частности, для функций двух переменных f(x, у )такой многочлен L_n(x, у )суммарной степени не выше и может быть построен по узлам (х _k, y_k )лишь при условии, что эти узлы не лежат на алгебраич. кривой порядка п.

Интерполяционные сплайны для функций многих переменных определяются на многомерной сетке при соответствующих изменениях по аналогии с одномерным случаем. И. функций используется для замены сложно вычисляемой функции другой, вычисляемой быстрее; для приближенного восстановления функции на всей области задания по значениям ее в отдельных точках; для получения сглаживающих функций., описывающих плавный процесс. Такого рода задачи имеют как самостоятельное значение, так и возникают в качестве вспомогательных при решении более сложных задач во многих областях науки и техники. И. функций применяется также для приближенного нахождения предельных значений функций, в задачах ускорения сходимости последовательностей и рядов и в других вопросах.

Численное решение нелинейных уравнений и систем. Общие идеи построения интерполяционных методов решения уравнения f(x)=0 и систем уравнений f_i(x₁, x₂. х _т) = 0, i=1, 2. т, одни и те же. Трудности задачи И. функций многих переменных особенно сказываются при исследовании и практич. использовании такого рода методов для большого числа уравнений. В основу получения интерполяционных методов решения уравнения f(x)=0 положена замена функции f(х)ее интерполяционным полиномом L _п (х)и последующим решением уравнения L_n(x)-0. Корни уравнения L_n(x)=0 берутся за приближенные решения уравнения f(х) = 0. Интерполяционный полином L_n(x)используется также при построении итерационных методов решения уравнения f(x) = 0.

Напр., взяв за х _п+1 корень линейного интерполяционного алгебраич. многочлена, построенного по значениям f(x_n )и f'( х _п )в узле х _п, или по значениям f(x_n-1) и f(x_n )в узлах х _п-1 и x_n приходят соответственно к методам Ньютона и секущих:

где f(x_n-1, х _п)- разделенная разность функции f(x)для узлов x_n-1 и х _п. При выполнении нек-рых условий последовательность значений х _п будет стремиться при

к решению уравнения f(x)=0. Другой подход к построению методов решения уравнения f(x)=0 основан на И. обратной функции х=g(y). Пусть в качестве интерполяционной формулы для функции x=g(y)взят интерполяционный алгебраич. многочлен Лагранжа

Численное интегрирование. Аппарат И. функций лежит в основе построения многих квадратурных и кубатурных формул. Такого рода формулы строятся путем замены интегрируемой функции на всей области или на ее составных частях интерполяционными полиномами того или иного вида и последующим интегрированием этих полиномов.

Напр., квадратурные формулы наивысшей алгебраич. степени точности, так наз. Гаусса квадратурные формулы

где р(х)- знакопостоянная весовая функция, получаются в результате замены функции f(x)интерполяционным алгебраич. многочленом, построенным по корням x_k ортогонального относительно веса р(х)многочлена степени п.

Если разделить весь отрезок интегрирования [ а, b]на четное число правных частей длины и на каждом сдвоенном частичном отрезке заменить f(х)ее квадратичным интерполяционным многочленом с узлами в крайних и средней точках, то придем к составной Симпсона формуле

Можно взять за основу и интерполяционные сплайны какой-то фиксированной степени. Изложенная выше схема построения формул для приближенного вычисления интегралов применима и в многомерном случае.

Численное дифференцирование. Формулы численного дифференцирования получаются в результате дифференцирования интерполяционных формул. При этом, как правило, заранее известна нек-рая априорная информация о дифференцируемой функции, касающаяся ее гладкости.

Пусть L_n(x)- интерполяционный полином нек-рого вида для функции f(x),a R_n(x)- остаток интерполяционной формулы:

пренебречь величиной R _п (i) (х), то это приведет к формуле для приближенного вычисления i-й производной функции f(x):

Формулы численного дифференцирования, в основе к-рых лежит И., получаются из приближенного равенства (3) в зависимости от выбора интерполяционного полинома L_n(x). При численном дифференцировании используются, как правило, приближенные значения функции в узлах; погрешность формул численного дифференцирования зависит не только от способа И. и шага И., но и от ошибки используемых значений функции в узлах. Напр., в случае линейного И. (1):

причем для остатка R’₁(x)имеет место представление:

Если f(x_k+1) и f(х _k )известны соответственно с погрешностями e_k+1 и то погрешность формулы (4) будет содержать еще член (e_k+1-e_k)/h, к-рый с уменьшением шага hвозрастает. При использовании формул численного дифференцирования шаг И. должен согласовываться с погрешностью значений функции. Поэтому на практике нередки случаи, когда известная с нек-рой погрешностью на густой сетке функция используется в данной задаче не во всех точках, а на более редкой сетке.

Численное решение интегральных уравнений. Неизвестная функция ,j(х)заменяется в интегральном уравнении какой-либо интерполяционной формулой (интерполяционным полиномом,, интерполяционным сплайном и т. д.) с узлами И. х _k, а приближенные значения для j( х _k )находятся из системы, полученной после подстановки вместо независимой переменной хузлов И. x_k.

Напр., для линейного интегрального уравнения Фредгольма 2-го рода

можно воспользоваться лагранжевым представлением интерполяционного многочлена:

где R_n(x)- остаток И.,

Замена функции j(х)в (5) ее интерполяционным многочленом L_n(x)и хна х _i, приводит к линейной системе уравнении

для нахождения приближенных значений j_i решения j(x)уравнения (5) в узлах x_i. В случае нелинейных интегральных уравнений приближенные значения j_i находятся соответственно из нелинейной системы.

Численное решение дифференциальных уравнений. Построение численных методов решения дифференциальных уравнений состоит в замене производных искомых функций интерполяционными формулами численного дифференцирования, а в ряде случаев и заменой интерполяционными формулами других функций и выражений, входящих в уравнения.

Пусть имеются формулы численного дифференцирования

для равноотстоящих узлов x_k= х ₀+kh, получаемые соответственно дифференцированием формул линейной и квадратичной И. (1) и (2). Тогда для обыкновенного дифференциального уравнения 2-го порядка

при нек-рых дополнительных условиях получается с учетом (6) уравнение в конечных разностях

из к-рого вместе с уравнениями, полученными из дополнительных условий, находятся приближенные значения y_k решения у(х)в узлах х _k.

Сведение дифференциальных уравнений с частными производными к соответствующим уравнениям в конечных разностях производится часто также с использованием формул численного дифференцирования.

Интерполяционный метод применим для решения дифференциальных уравнений, записанных в интегральной форме. Напр., для нахождения приближенного решения задачи Коши

получаемые заменой функции под знаком интеграла в равенстве

интерполяционным полиномом и последующим интегрированием. В частности, таким образом получены формулы Адамса для уравнения 1-го порядка (7) формулы Стёрмера для уравнений 2-го порядка и т. д.

Такой подход позволяет, строить вычислительные алгоритмы для широкого класса дифференциальных уравнений в том числе и для уравнений в частных производных. Исследование разрешимости, точности и устойчивости решения возникающих конечно разностных уравнений представляет собой основную и наиболее трудную часть теории численного решения дифференциальных уравнений.

Интерполирование операторов и некоторые общие подходы к построению численных методов. Построение численных методов решения математич. задач, записанных в виде у=Ах, где элементы хи у принадлежат нек-рым множествам Xи Y, а А- заданный оператор, состоит в замене множеств Xи Y и оператора Аили только нек-рых из этих трех объектов другими, удобными для вычислительных целей. При этом замена должна быть сделана так, чтобы решение новой задачи 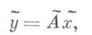состоящей в нахождении или было в каком-то смысле близко к решению первоначальной задачи. Один из способов замены оператора Аего приближением состоит в использовании интерполирования операторов. Имеются различные формулировки задачи И” операторов. Линейный интерполяционный оператор L₁(F; x )для данного оператора записывается в виде

Данное определение оператора разделенной разности в ряде случаев конкретизируется. С использованием линейного И. (8) “метод секущих” для уравнения F(x)=0 записывается в виде

И. функционалов используется при построении приближенных методов вычисления континуальных интегралов, для нахождения экстремальных значений функционалов и ряда других задач.

Напр., приближенные интерполяционные формулы для вычисления континуальных интегралов имеют вид

при этом интеграл от интерполяционного полинома L_n[F; x]для нек-рых мер m может вычисляться точно или сводиться к конечномерным интегралам. Интерполяционный полином L₁[F; x], когда Xесть пространство непрерывных на отрезке [ а, b]функций С[ а, b], представляется в виде интеграла Стилтьеса

Применение И. к нахождению экстремальных значений функционалов может быть проиллюстрировано двумя интерполяционными аналогами метода градиента для нахождения локальной точки безусловного минимума функционала F(x), определенного на нек-ром гильбертовом пространстве. Первый из этих методов получается, если в градиентном методе заменить grad F(x_n )на F(x_n-1, x_n), т. е.

Второй метод использует градиент интерполяционного полинома. По приближениям x_n-2, x_n-1, х _п к экстремальной точке х* функционала F(x)строится квадратичный интерполяционный функционал

где F(x_n-2, х _n-1, х _п)- разделенная разность 2-го порядка функционала F(x)относительно узлов х _n-2, х _n-1 х _п, и новое приближение х _п+1 находится по формуле

Итерационные методы (9) и (10) используют соответственно два и три начальных приближения.

Применение И. функционалов и операторов для построения вычислительных алгоритмов решения конкретных задач основано на использовании интерполяционных формул с малой величиной погрешности. Такого рода формулы должны строиться для отдельных классов функционалов и операторов с учетом специфики этих классов.

Полезное

Смотреть что такое “ИНТЕРПОЛИРОВАНИЕ” в других словарях:

интерполирование — сущ., кол во синонимов: 1 • интерполяция (4) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов

Интерполирование — [interpolation] отыскание промежуточной ( неизвестной) величины динамического ряда (например, некоторого элемента временной последовательности). И. часто осуществляется с помощью выровненного графика этого ряда, а также аналитически. Аналогичная … Экономико-математический словарь

интерполирование — Отыскание промежуточной ( неизвестной) величины динамического ряда (например, некоторого элемента временной последовательности). И. часто осуществляется с помощью выровненного графика этого ряда, а также аналитически. Аналогичная процедура, если… … Справочник технического переводчика

Интерполирование — О функции, см.: Интерполянт. Интерполяция в вычислительной математике способ нахождения промежуточных значений величины по имеющемуся дискретному набору известных значений. Многим из тех, кто сталкивается с научными и инженерными расчётами часто … Википедия

ИНТЕРПОЛИРОВАНИЕ — ИНТЕРПОЛЯЦИЯ, ИНТЕРПОЛИРОВАНИЕ один из способов приближенного вычисления, когда по ряду величин данного математического выражения определяют промежуточные члены и т. образ. находят искомые неизвестные; 2) вставка в рукопись к. н. сочинения не… … Словарь иностранных слов русского языка

ИНТЕРПОЛИРОВАНИЕ — интерполяция, в простейшем, классическом смысле конструктивное восстановление (быть может, приближенное) функции определенного класса по известным ее значениям или значениям ее производных в данных точках. Пусть даны n+l точек сегмента D=[ а, b] … Математическая энциклопедия

Интерполирование — в математике один из важнейших способов приближенного вычисления. Задача И. заключается в том, чтобы по данным величинам некоторой функции для известных значений переменных независимых (аргументов) найти величину функции для произвольного… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

Интерполирование — ср. 1. процесс действия по несов. гл. интерполировать 2. Результат такого действия. Толковый словарь Ефремовой. Т. Ф. Ефремова. 2000 … Современный толковый словарь русского языка Ефремовой

интерполирование — интерпол ирование, я … Русский орфографический словарь

интерполирование — способ заполнения недостающих членов какого либо статистического ряда; предпосылкой к применению этого способа является допущение, что то строение ряда, которое может быть установлено на основании соотношения известных составных частей (членов) … Справочный коммерческий словарь

Источник