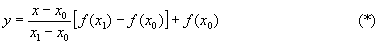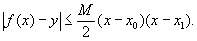Интерполировать что это простыми словами
Интерполяция – что это?
Что такое интерполяция простыми словами
Пожалуй, сегодня мы не сможем найти смартфон, даже в самой бюджетной ценовой категории, который оказался бы лишенным встроенной камеры. Современные технологии позволяют получать сверхточные снимки просто космического разрешения.
Интерполяция – с точки зрения математической науки, это высокотехнологичный способ увеличения полученных фотографий, используя особые алгоритмы. Говоря конкретнее, это поиск промежуточных числовых значений, осуществляемый по ряду дискретных параметров. По этому же принципу, работают многие специализированные программы для обработки изображений и графики, вроде Adobe Photoshop.
К счастью, современные телефоны в большинстве обладают очень быстрыми процессорами, позволяющими пользователю не замечать того, как софт его гаджета обрабатывает свежий снимок.
В какой-то степени, это процесс можно сравнить с работой линз лупы. Функционал нашего телефона не позволяет улучшить такие параметры снимка, как четкость или резкость. Однако имеющиеся возможности позволяют увеличить изображение до нужных нам размеров.
Как правило, пределом получаемого изображения является заявление производителя о матрице встроенной камеры: «8, 13, 16, 20 мп. и т.д». В данном случае, эта цифра говорит именно о способностях программного обеспечения девайса интерполировать картинку имеющую изначально низкое разрешение.
Самым базовым и распространенным видом интерполирования является так называемый «метод ближайшего соседа». Данный метод входит в группу самых простейших алгоритмов. Суть метода заключается в умножении на 2 каждого пикселя изображения, осуществляемого в ходе специальных математических расчетов и алгоритмов.
Данный метод не требователен к ресурсам гаджета, и не требует от графического процессора телефона особых вычислительных мощностей.
Следующим методом является билинейная интерполяция. Здесь, камерой фиксируется четыре точки в пространстве, на основании которых в дальнейшем будет рассчитываться положение каждого пикселя изображения.
В итоге получается усреднение ряда параметров 4 пикселей, окружающих каждую точку изображения. С помощью данного метода можно сгладить различные переходы цвета, переходы между границами объекта. Такие изображения, по своему качеству значительно превосходят многие картинки, полученные с помощью первого метода.
Одним из самых сложных методов интерполяции считается бикубический метод здесь, значение каждого искомого пикселя определяется по шестнадцати ближайшим точкам. Те из них, что располагаются ближе всего к искомой становятся после расчетов и обработки наиболее весомыми.
Бикубическая интерполяция используется в самых современных смартфонах, оснащенных наиболее производительными камерами, позволяющих получить лучшее изображение. Использование данного метода требует от смартфона наличия процессора с высокими вычислительными мощностями, а также камеры, матрица которой имеет высокое разрешающую способность.
О достоинствах и недостатках
В кинематографе, мы часто видим, как камеры на улицах фиксируют лица каких-нибудь плохих парней, моментально схватывая все черты лица этого человека, со скоростью света передавая все данные на какой-нибудь удаленный компьютер.
Алгоритмы с помощью методов интерполяции увеличивают картинку, после чего проводится распознавание лица и поиск его в каких-нибудь сверхсекретных базах данных.
Но,на самом деле, как бы ни были высоки возможности интерполяции камер современных устройств, они не способны добавить или восстановить мелкие детали на изображении.
С помощью интерполяции происходит лишь увеличение исходной картинки до «воспринимаемого» уровня, и только.
О возможных проблемах
Самыми распространенными дефектами применения интерполяционной обработки изображения являются те, что возникают при масштабировании, а именно «ореол», эффекты размытости и ступенчатости. Имеющиеся методы обработки позволяют, каждый с большим или меньшим успехом, соблюдать некоторый баланс влияния этих недостатков на качество фото.
Проблема еще и заключается в том, что борьба с одним из них неминуемо влечет к обострению другого. Попытка уменьшить эффект ступенчатости может привести к излишней размытости и появлению эффекта ореола на снимке.
Калибровка резкости снимка нередко приводит к увеличению размытости и т.п. Помимо самых часто встречающихся дефектов, использование методов интерполяции приводит к возникновению «графических шумов», которые особо сильно проявляются при значительном увеличении картинки.
В этом случае изображение может пестрить «случайными» пикселями или возникновением чуждых для данной экспозиции текстур.
Значение слова «интерполировать»
Источник (печатная версия): Словарь русского языка: В 4-х т. / РАН, Ин-т лингвистич. исследований; Под ред. А. П. Евгеньевой. — 4-е изд., стер. — М.: Рус. яз.; Полиграфресурсы, 1999; (электронная версия): Фундаментальная электронная библиотека
ИНТЕРПОЛИ’РОВАТЬ [тэ], рую, руешь, сов. и несов., что (науч.). Сделать (делать), произвести (производить) интерполяцию чего-н.
Источник: «Толковый словарь русского языка» под редакцией Д. Н. Ушакова (1935-1940); (электронная версия): Фундаментальная электронная библиотека
интерполи́ровать
1. филол. произвольно или случайно вставлять (вставить) в текст при переписке или в процессе редактирования
2. матем. находить (найти) промежуточные значения какой-либо величины по некоторым известным её значениям
Делаем Карту слов лучше вместе
Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать Карту слов. Я отлично умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!
Спасибо! Я обязательно научусь отличать широко распространённые слова от узкоспециальных.
Насколько понятно значение слова контральто (существительное):
Синонимы к слову «интерполировать»
Предложения со словом «интерполировать»
Понятия, связанные со словом «интерполировать»
Отправить комментарий
Дополнительно
Предложения со словом «интерполировать»
Церковь определяла важнейшие события месяца, сезона, года, упорядочивая всё земное и мирское, интерполируя природные циклы в пространство литургического календаря.
Именно изучив – интерполировав мысли автора на события своей жизни и сделав выводы, корректировки и наметив новые планы.
Теперь науке осталось всего-навсего интерполировать этот успех и остановить прекрасное мгновенье не только для наблюдения, но и для живого участия, пребывания в нём.
Интерполяция
Из Википедии — свободной энциклопедии
Интерполя́ция, интерполи́рование (от лат. inter–polis — «разглаженный, подновлённый, обновлённый; преобразованный») — в вычислительной математике нахождение неизвестных промежуточных значений некоторой функции, по имеющемуся дискретному набору её известных значений, определенным способом. Термин «интерполяция» впервые употребил Джон Валлис в своём трактате «Арифметика бесконечных» (1656).
Многим из тех, кто сталкивается с научными и инженерными расчётами, часто приходится оперировать наборами значений, полученных опытным путём или методом случайной выборки. Как правило, на основании этих наборов требуется построить функцию, на которую могли бы с высокой точностью попадать другие получаемые значения. Такая задача называется аппроксимацией. Интерполяцией называют такую разновидность аппроксимации, при которой кривая построенной функции проходит точно через имеющиеся точки данных.
Существует также близкая к интерполяции задача, которая заключается в аппроксимации какой-либо сложной функции другой, более простой функцией. Если некоторая функция слишком сложна для производительных вычислений, можно попытаться вычислить её значение в нескольких точках, а по ним построить, то есть интерполировать, более простую функцию. Разумеется, использование упрощенной функции не позволяет получить такие же точные результаты, какие давала бы первоначальная функция. Но в некоторых классах задач достигнутый выигрыш в простоте и скорости вычислений может перевесить получаемую погрешность в результатах.
Интерполяция
Интерполя́ция, интерполи́рование — в вычислительной математике способ нахождения промежуточных значений величины по имеющемуся дискретному набору известных значений.
Многим из тех, кто сталкивается с научными и инженерными расчётами часто приходится оперировать наборами значений, полученных опытным путём или методом случайной выборки. Как правило, на основании этих наборов требуется построить функцию, на которую могли бы с высокой точностью попадать другие получаемые значения. Такая задача называется аппроксимацией. Интерполяцией называют такую разновидность аппроксимации, при которой кривая построенной функции проходит точно через имеющиеся точки данных.
Существует также близкая к интерполяции задача, которая заключается в аппроксимации какой-либо сложной функции другой, более простой функцией. Если некоторая функция слишком сложна для производительных вычислений, можно попытаться вычислить её значение в нескольких точках, а по ним построить, то есть интерполировать, более простую функцию. Разумеется, использование упрощенной функции не позволяет получить такие же точные результаты, какие давала бы первоначальная функция. Но в некоторых классах задач достигнутый выигрыш в простоте и скорости вычислений может перевесить получаемую погрешность в результатах.
Следует также упомянуть и совершенно другую разновидность математической интерполяции, известную под названием «интерполяция операторов». К классическим работам по интерполяции операторов относятся теорема Рисса-Торина (Riesz-Thorin theorem) и теорема Марцинкевича (Marcinkiewicz theorem), являющиеся основой для множества других работ.
Содержание
Определения
Рассмотрим систему несовпадающих точек 
(
) из некоторой области 
. Пусть значения функции 
известны только в этих точках:
Задача интерполяции состоит в поиске такой функции 
из заданного класса функций, что
Пример
1. Пусть мы имеем табличную функцию, наподобие описанной ниже, которая для нескольких значений 
определяет соответствующие значения :
|  |
|---|---|
| 0 | 0 |
| 1 | 0,8415 |
| 2 | 0,9093 |
| 3 | 0,1411 |
| 4 | −0,7568 |
| 5 | −0,9589 |
| 6 | −0,2794 |
Интерполяция помогает нам узнать какое значение может иметь такая функция в точке, отличной от указанных (например, при x = 2,5).
К настоящему времени существует множество различных способов интерполяции. Выбор наиболее подходящего алгоритма зависит от ответов на вопросы: как точен выбираемый метод, каковы затраты на его использование, насколько гладкой является интерполяционная функция, какого количества точек данных она требует и т. п.
2. Найти промежуточное значение (способом линейной интерполяции).
| 6000 | 15.5 |
| 6378 | ? |
| 8000 | 19.2 |
Способы интерполяции
Интерполяция методом ближайшего соседа
Простейшим способом интерполяции является интерполяция методом ближайшего соседа.
Интерполяция многочленами
На практике чаще всего применяют интерполяцию многочленами. Это связано прежде всего с тем, что многочлены легко вычислять, легко аналитически находить их производные и множество многочленов плотно в пространстве непрерывных функций (теорема Вейерштрасса).
Обратное интерполирование (вычисление x при заданном y)
Интерполяция функции нескольких переменных
Другие способы интерполяции
Смежные концепции
См. также
Полезное
Смотреть что такое «Интерполяция» в других словарях:
ИНТЕРПОЛЯЦИЯ — 1) способ определять по ряду данных величин какого либо математического выражения промежуточные его величины; так напр., по дальности полета ядра при угле возвышения оси пушечного канала в 1°, 2°, 3°, 4° и т. д. можно определить помощью… … Словарь иностранных слов русского языка
интерполяция — вставка, интерполирование, включение, отыскание Словарь русских синонимов. интерполяция см. вставка Словарь синонимов русского языка. Практический справочник. М.: Русский язык. З. Е. Александрова. 2 … Словарь синонимов
интерполяция — Вычисление промежуточных значений между двумя известными точками. Например: linear линейная интерполяция exponential экспоненциальная интерполяция Процесс вывода цветного изображения, когда пикселы, относящиеся к области между двумя цветными… … Справочник технического переводчика
Интерполяция — (interpolation) Оценка значения неизвестной величины, находящейся между двумя точками ряда известных величин. Например, зная показатели населения страны, полученные при проведения переписи населения, проводившейся с интервалом в 10 лет, можно… … Словарь бизнес-терминов
Интерполяция — с латинского собственно «подделка». Так называются ошибочные поправки или позднейшие вставки в рукописях, сделанные переписчиками или читателями. Особенно часто этот термин употребляется в критике рукописей античных писателей. В этих рукописях… … Литературная энциклопедия
Интерполяция — нахождение промежуточных значений некоторой закономерности (функции) по ряду известных ее значений. По английски: Interpolation См. также: Преобразования данных Финансовый словарь Финам … Финансовый словарь
интерполяция — и, ж. interpolation f. < лат. interpolatio изменение; переделка, искажение. 1. Вставка позднейшего происхождения в каком л. тексте, не принадлежащая оригиналу. БАС 1. В древних рукописях много интерполяций, внесенных переписчиками. Уш. 1934. 2 … Исторический словарь галлицизмов русского языка
ИНТЕРПОЛЯЦИЯ — (interpolatio), пополнение эмпйрич. ряда значений какой либо величины недостающими промежуточными значениями ее. Интерполирование может быть произведено тремя способами: математич., графич. и логическим. В основе их лежит общая им гипотеза о том … Большая медицинская энциклопедия
ИНТЕРПОЛЯЦИЯ — (от латинского interpolatio изменение, переделка), отыскание промежуточных значений величины по некоторым известным ее значениям. Например, отыскание значений функции y = f(x) в точках x, лежащих между точками x0 и xn, x0 … Современная энциклопедия
ИНТЕРПОЛЯЦИЯ — в филологии изменение первоначального текста; вставка переписчиком или переводчиком в текст слов или фраз, отсутствовавших в оригинале … Большой Энциклопедический словарь
Интерполяция
в математике и статистике, отыскание промежуточных значений величины по некоторым известным её значениям. Например, отыскание значений функции f (x) в точках х, лежащих между точками (узлами И.) x0
линейной функции, совпадающей с f (x) в точках х = x0 и х = x1. Задача И. со строго математической точки зрения является неопределённой: если про функцию f (x) ничего неизвестно, кроме её значений в точках x0, x1. хn, то её значение в точке х, отличной от всех этих точек, остаётся совершенно произвольным. Задача И. приобретает определённый смысл, если функция f (x) и её производные подчинены некоторым неравенствам. Если, например, заданы значения f (x0) и f (x1) и известно, что при x0
Более сложные Интерполяционные формулы имеет смысл применять лишь в том случае, если есть уверенность в достаточной «гладкости» функции, т. е. в том, что она обладает достаточным числом не слишком быстро возрастающих производных.
Кроме вычисления значений функций, И. имеет и многочисленные другие приложения (например, при приближённом интегрировании, приближённом решении уравнений, в статистике при сглаживании рядов распределения с целью устранения случайных искажений).
Лит.: Гончаров В. Л., Теория интерполирования и приближения функций, 2 изд., М., 1954; Крылов А. Н., Лекции о приближённых вычислениях, 6 изд., М., 1954; Юл Дж. Э., Кендэл М. Дж., Теория статистики, пер. с англ., 14 изд., М., 1960.
Интерполя́ция (от лат. interpolatio — подновление, изменение)
вставка, поправка в первоначальный текст, не принадлежащая автору. Большое значение имели И. в текстах сочинений римских юристов, включенных в состав Дигест (См. Дигесты). И. оказались необходимыми для устранения противоречий в работах этих юристов, а также положений и оценок, чуждых эпохе императора Юстиниана; применялись различные виды И.: замена или уточнение нормы права; замена термина или его устранение; лексическое изменение и т. д. Впервые обнаружены в средние века гуманистами.