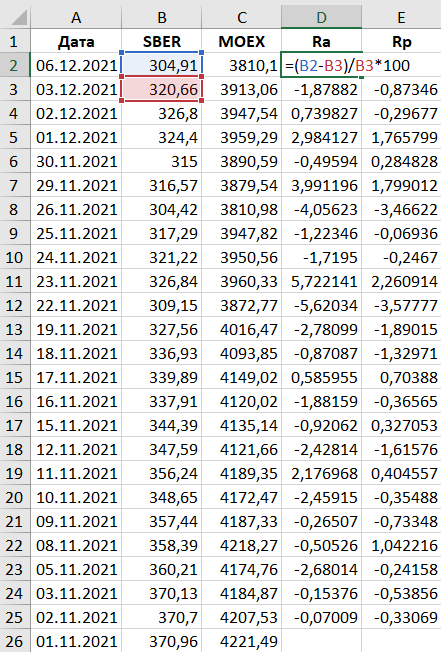
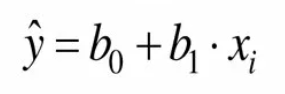Интерпретация бета коэффициента для акций конкретной организации при 1 означает что
Коэффициент Бета и его применение для оценки инвестиционных рисков при формировании портфеля акций
Этот коэффициент вычисляется как отношение изменения доходности акции к изменению доходности рынка в целом. Коэффициент Бета применяется для оценки риска инвестиций в те или иные акции.
Он был разработан Уильямом Шарпом и предложен к применению в рамках портфельной теории Марковица (использование данного коэффициента позволяет подбирать в свой портфель бумаги с приемлемым для инвестора уровнем риска).
Использование коэффициента Бета позволяет формировать инвестиционный портфель из бумаг сочетающих в себе наибольшие показатели доходности с наименьшим уровнем риска.
Формула расчёта
Формула для расчёта коэффициента β выглядит следующим образом:
Как видите без базовых знаний в области высшей математики здесь разобраться довольно трудно. Поэтому объясняю на пальцах. Суть расчёта сводится к тому, чтобы сопоставить динамику изменения курсовой стоимости конкретных акций с динамикой рынка акций в целом.
Если волатильность рассматриваемых бумаг превышает волатильность по рынку в целом, то это говорит о том, что они более чувствительны к изменению конъюнктуры. Это, в свою очередь, говорит нам о том, что инвестиции в них подвержены большему риску.
При этом нет нужды охватывать весь рынок целиком и забивать в формулу значения для каждой акции его составляющей. В данном случае достаточно использовать значение фондового индекса (который сам по себе представляет среднее значение курсовой стоимости акций принадлежащих к определённой отрасли или объединённых по какому-либо другому признаку).
Для акций российских эмитентов в данном случае можно применять индекс Мосбиржи, а для бумаг фондового рынка США, например, будет актуален индекс S&P500.
Индексы Мосбиржи и S&P500
Коэффициент Бета может быть рассчитан как для отдельных акций, так и для портфеля инвестора в целом. Бета коэффициент портфеля вычисляется как средняя величина Бета коэффициентов акций в него входящих (с учетом их весов).
Как же рассчитать данный коэффициент человеку не отягощённому знаниями в области высшей математике? Спешу вас успокоить, перефразируя высказывание одного из героев бессмертной комедии Гайдая, скажу: «Всё уже посчитано до нас!»
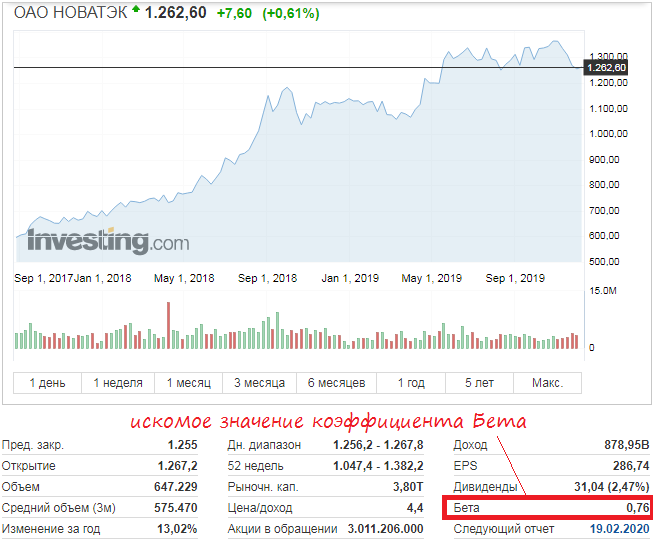
Вы легко можете найти данные по этому коэффициенту на множестве сайтов посвящённым тематике инвестиций и биржевой торговли. Вот например картинка с графиком и основными показателями акций ОАО Новатэк, взятая с сайта investing.com:
Как интерпретировать значение коэффициента
В целом значение коэффициента интерпретируется следующим образом:
β>1 — дает инвестору сигнал о том, что изменение доходности по акции превышает изменение среднего дохода по рынку в целом. А это в свою очередь значит, что колебания доходности по акции больше чем колебания среднего дохода по рынку и, значит, уровень риска по акции превышает средний уровень риска по по акциям других компаний.
На фондовом рынке США существует понятие high-beta stock. Так называют акции волатильность которых значительно превышает средние значения по остальным торгуемым бумагам. Такие акции представляют интерес в основном для краткосрочных трейдеров, которые предпочитают финансовые инструменты с широкой амплитудой движения, позволяющей взять как можно больше прибыли в ограниченный промежуток времени. Долгосрочные инвесторы относятся к таким бумагам с осторожностью.
β=1 — дает инвестору информацию о том, что изменение доходности по акции идет в ногу с изменением доходности по рынку в целом. Соответственно, уровень риска по акции сопоставим с уровнем риска по другим бумагам представленным на рынке.
0 1. Умеренный стиль инвестирования предполагает формирование портфеля из акций с коэффициентом Бета приблизительно равным единице.
Для портфеля в целом, коэффициент β рассчитывается исходя из отдельных коэффициентов для бумаг входящих в его состав, с учётом веса каждой из них:
βп = β1W1 + β2W2 +…+ βn*Wn, где
βi – коэффициент Бета для i-той акции в составе портфеля;
Wi – вес i-той акции;
n – общее число акций в составе портфеля.
При этом ожидаемую величину доходности портфеля можно рассчитать по формуле:
Rp – ожидаемая доходность инвестиционного портфеля;
Rm – средняя доходность по рынку (по фондовому индексу взятому для расчёта β).
Недостатки коэффициента Бета
Мы с вами подробно рассмотрели все те преимущества которые может дать применение этого коэффициента при формировании инвестиционного портфеля, а теперь, для полной объективности картины, давайте остановимся на его недостатках.
В основе портфельной теории Марковица лежит предположение о том, что рынки по своей природе являются эффективными. Не вдаваясь в подробности можно сказать, что это означает примерно следующее:
При подобных исходных данных можно говорить о строгом соответствии уровня доходности тому риску, которому подвергаются инвестиции. Что собственно и отражено в вышепредставленной формуле коэффициента β выведенной одним из сторонников теории эффективного рынка, Уильямом Шарпом.
На деле же получается так, что фондовый рынок нельзя назвать эффективным. В частности это доказывают работы лауреата Нобелевской премии в области экономики, Ричарда Талера. В них чётко доказывается факт того, что поведение большинства участников рынка далеко от рационального.
Кроме этого, ввиду огромного количества и неравномерности распространения информации нельзя говорить о том, что вся она имеет своё отражение в стоимости торгуемых на финансовых рынках активов.
Ещё одним недостатком коэффициента является то, что при его расчёте используется предположение о нормальном распределении доходности портфеля (что, мягко говоря, не является истиной). На деле такое положение вещей встречается довольно редко и в большинстве случаев ни о каком нормальном распределении, в данном контексте, не может быть и речи.
В заключение следует сказать ещё и о том, что значение коэффициента зависит от того временного периода данные за который были положены в его расчёт. Этот факт следует обязательно учитывать как для отдельно взятых акций, так и при сравнении их друг с другом.
Послесловие
Мы рассмотрели один из важнейших финансовых коэффициентов позволяющих оценить относительную степень риска инвестиций в те или иные акции. Несмотря на описанные выше недостатки, рассматриваемый коэффициент, при грамотном использовании, вполне можно применять для формирования своего инвестиционного портфеля.
Бета коэффициент
Риски: без их расчета на фондовом рынке никуда. В предыдущих статьях мы разбирали стандартное отклонение и дисперсию (в статье волатильность), как меру риска, сегодня поговорим о коэффициенте бета.
СОДЕРЖАНИЕ СТАТЬИ:
Коэффициент бета β – показатель ценной бумаги (портфеля), который рассчитывается как мера рыночного риска и дает оценку относительного изменения доходности ценной бумаги (портфеля) по сравнению с доходностью рынка в целом. Проще говоря, этот коэффициент показывает, как рынок воздействует на ценную бумагу.
Коэффициент бета необходим для:
– определения рыночного риска актива (портфеля) относительно рынка в целом;
– составление портфеля, нейтрального к риску;
– расчета оценки стоимости капитала.
Формула беты и ее возможные значения
Общепринятый подход к оценке параметра «бета акции» основывается на регрессионном анализе доходности акции относительно доходности фондового индекса.
Классическая бета или, как ее еще называют «сырая», необработанная бета (raw beta):
β – коэффициент бета;
cov (r, p) – ковариация ценной бумаги и портфеля (вместо портфеля часто применяют рыночный индекс, например, индекс Московской Биржи и индекс РТС);
r – доходность актива (ценной бумаги);
p – доходность портфеля (фондового индекса);
σp 2 – дисперсия портфеля (фондового индекса).
Значения, которые может принимать бета:
β = 1 – доходность такой бумаги будет изменяться одинаково с доходностью рынка (фондового индекса);
β > 1 – доходность (а также изменчивость) таких бумаг очень чувствительна к изменению рынка. Такие активы больше подвержены риску, но потенциально более доходны. В целом, такие ценные бумаги можно назвать агрессивными;
β – коэффициент бета;
ri – доходность актива в i-ый момент времени;
pi – доходность портфеля (индекса) в i-ый момент времени;
r ср – доходность актива в i-ый момент времени;
р ср – доходность портфеля (индекса) в i-ый момент времени;
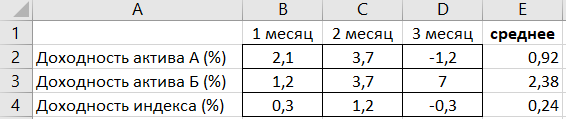
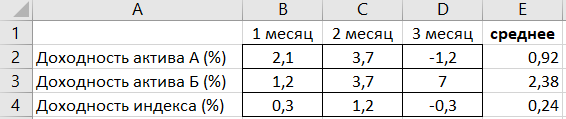
Пример для расчета беты
Совершим расчет беты для актива А
Тот же пример, но с расчетом в Excel
– с помощью опции вставить функцию :
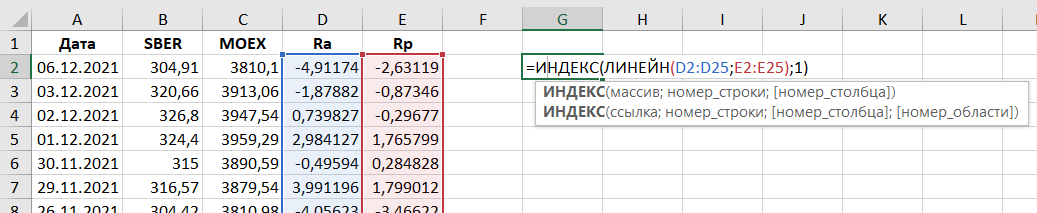
А именно, =ИНДЕКС(ЛИНЕЙН(B2:D2;B4:D4);1) = 3,14
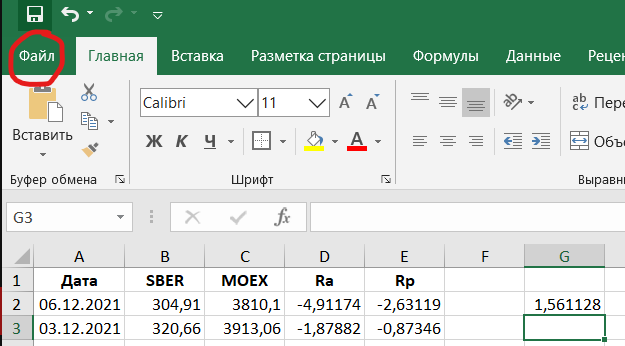
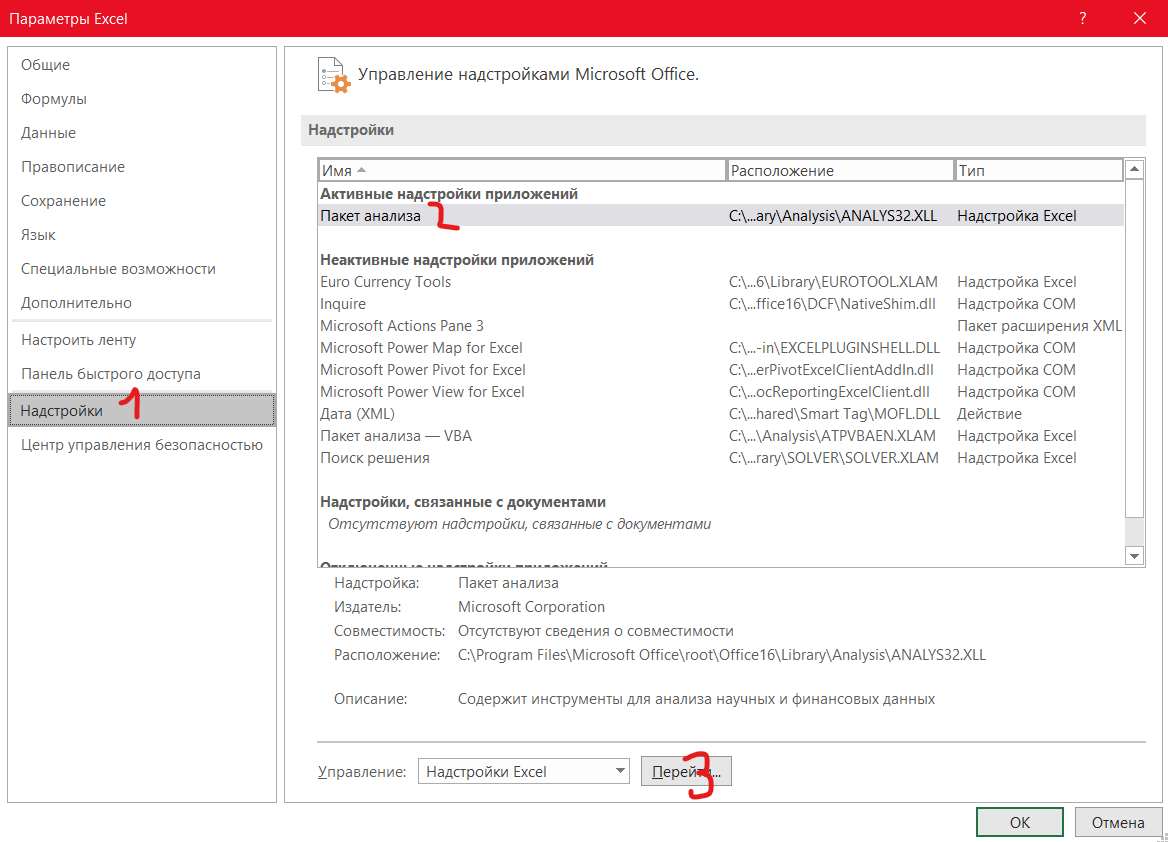
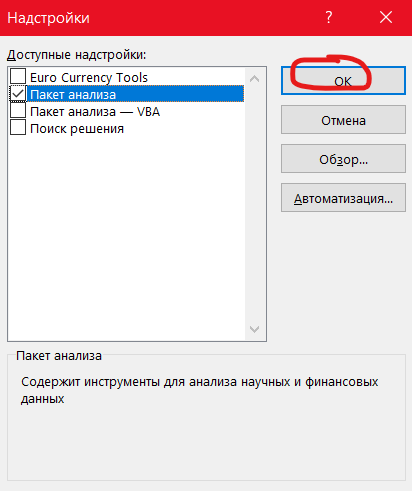
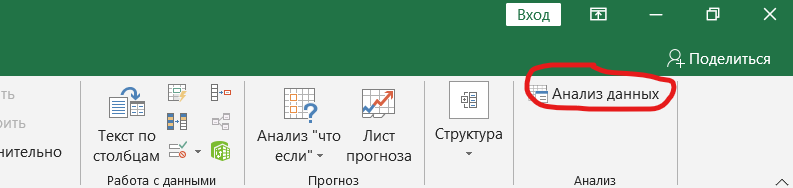
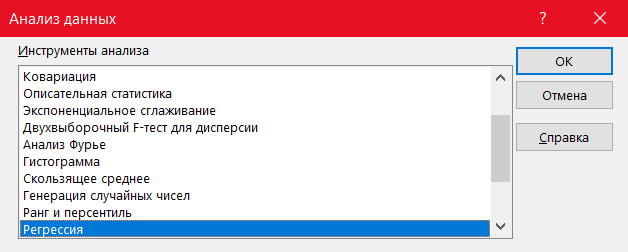
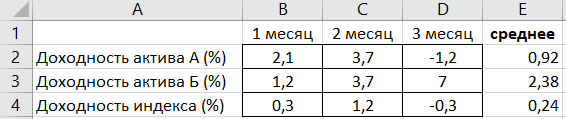
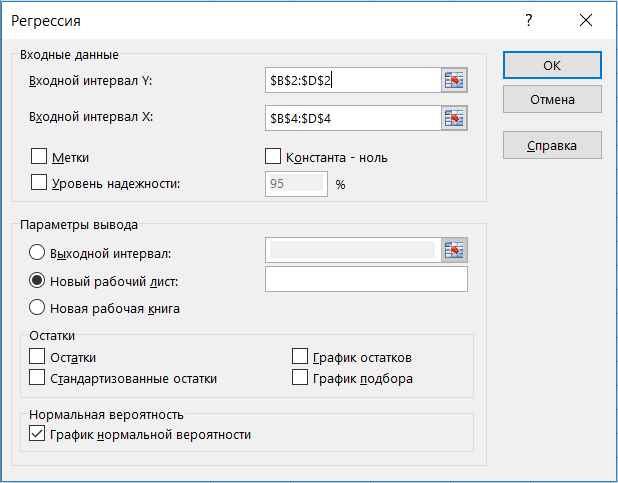
– с помощью пакета «анализ данных» в Excel (пример только для актива А):
Сначала нужно проверить наличие пакета «анализ данных», если не стоит, то установить в файл → параметры → надстройки. Затем в пакете выбираем опцию регрессия и делаем следующие манипуляции, согласно фото
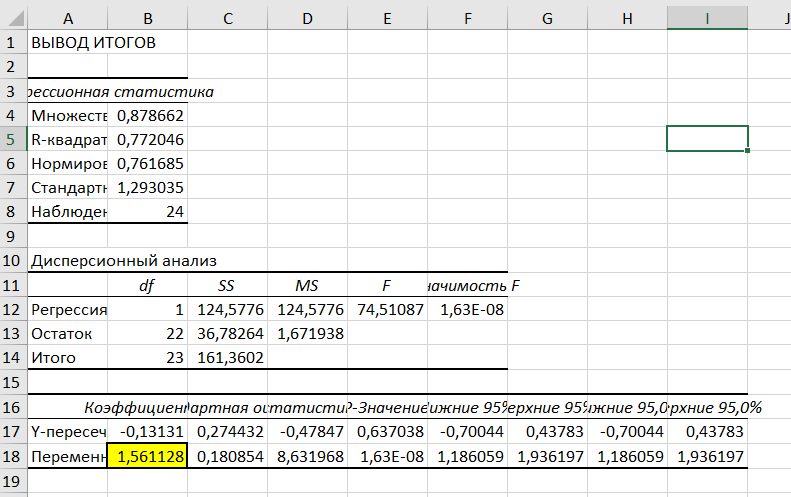
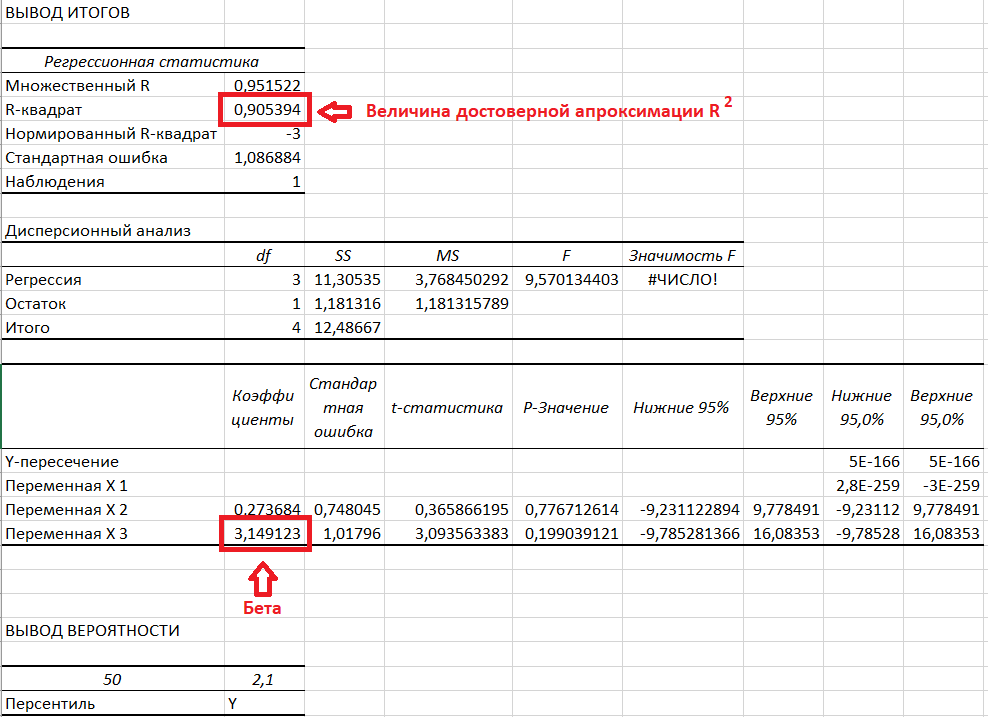
Получаем следующие значения:
Как видим значения сошлись.
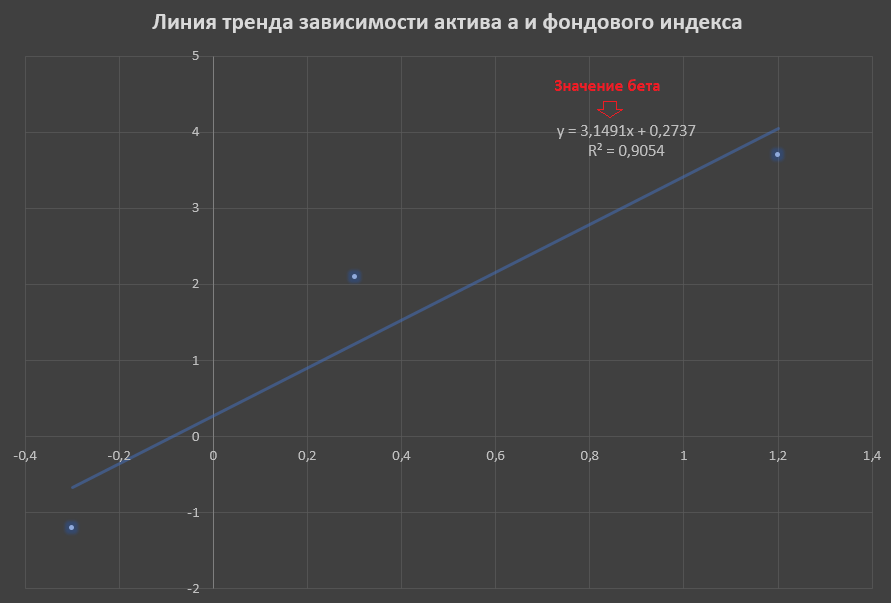
Теперь с помощью Excel покажем графическое представление бета:
На основании данных, приведенных в таблице значений по месяцам построим точечный график зависимости доходности актива А от фондового индекса (в примере будем делать только для актива А)
Бета портфеля, бета – нейтральный портфель.
Бета портфеля показывает совокупный риск вашего собственного портфеля относительно рынка. Важно понимать, как его рассчитать, чтобы составить портфель максимально нетерпимый к риску, а точнее, независимый от рынка.
Формула расчета беты портфеля:
βп – коэффициент бета портфеля;
Θi – вес i-ого актива в портфеле;
βi – бета i-ого актива в портфеле.
Рассчитаем бету портфеля, в активе которого есть актив А и Б
Бета-нейтральный портфель, это частный случай, при котором бета портфеля равна нулю
Как же его получить?
Надо включить в портфель в дополнение к бумагам с положительной бетой, бумаги с отрицательной бетой и с такими весами, чтобы при подсчете беты портфеля она получилась равной нулю.
На практике достаточно мало портфелей имеют бету меньше нуля, но практически к ним можно отнести акции золотодобывающих компаний, т.к. в период кризисов они не просто не падают, а показывают существенный рост. (В России – это акций ПАО «Полюс» и ПАО «полиметалл»).
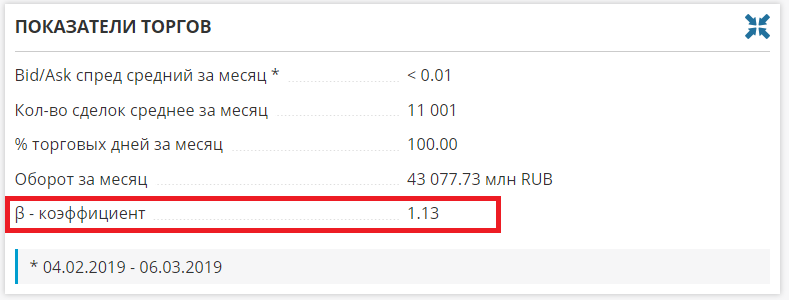
Если нет желания считать бету самостоятельно, то посмотреть ее можно здесь:
Бету всегда можно найти на сайте Московской Биржи, по ссылке:
На сайте investfunds.ru
Недостатки использования беты и их модификации
Как и у любой модели, у методики применения беты есть свои преимущества и недостатки. Многие эксперты пришли к выводу, что для любой акции ее бета не является устойчивым во времени показателем и поэтому не может служить точной оценкой будущего риска.
Для российского рынка характерны следующие недостатки применения модели классической беты:
1) Низкий показатель детерминации. Показывает долю риска, который присущ рыночному риску;
2) Мало информативные значения беты (которые нельзя применять) для акций малой ликвидности и капитализации;
3) Не применим к бумагам, у которых нету исторических цен (на длительном отрезке времени);
4) Коэффициент бета не может предусмотреть реальных положений дел в компаниях.
По всем этим причинам, описанным выше, были выведены модифицированные беты:
Наиболее популярные модификации представлены ниже (2 формулы)
Бета согласно Маршалу Блюму
Его расчеты показали, что со временем величина бета-портфеля приближается к единице, а внутренний риск компании стремится к среднеотраслевому или среднерыночному. Такую бету используют многие инвестиционные банки мира.
βбл – бета по Маршалу Блюму;
β – коэффициент классической, сырой беты;
Бета согласно Шоулза-Виллимса
βшв – бета по Маршалу Блюму;
– коэффициенты бета для предыдущего, текущего и последующего периода;
– коэффициент автокорреляции рыночной доходности.
Бета-коэффициент (β) при анализе акций — что это и как работает
В этой статье вы познакомитесь с коэффициентом β, который чаще всего рассчитывается для акций (но может и для любого актива) при сравнение их волатильности. Также этот показатель помогает рассчитать риски и доходность инвестиционных портфелей.
1. Что такое бета-коэффициент на рынке простыми словами
Бета-коэффициент впервые предложил Шарп. Он является лишь статистическим показателем. Его исторические данные не гарантируют, что и в будущем соотношения будут такими же.
Это может быть сравнение нескольких портфелей: российских и зарубежных акций, золота или облигационных наборов. Искать зависимость можно между любыми инструментами на бирже.
Например, если фондовый индекс вырос на 1% и акция выросла на 1%, то в этом случае β = 1, поскольку движение биржевых котировок полностью копируют индекс. Если же первый вырос на 1%, а второй на 2,5%, то в этом случае β = 2,5, что говорит о том, что акция волатильнее индекса в два с половиной раза. Она будет расти и падать сильнее. Это даёт премию к доходности при бычьем рынке и большие риски при падающем.
Вместо Var (p) в знаменателе часто можно увидеть σ 2 (дисперсия портфеля или фондового индекса).
Более подробная формула выглядит следующим образом
Как можно интерпретировать значения β




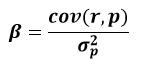

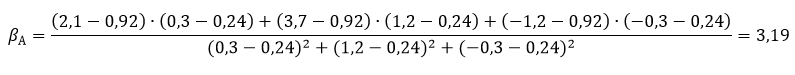
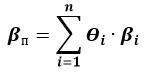
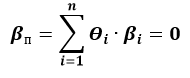

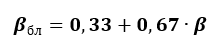
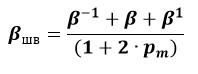
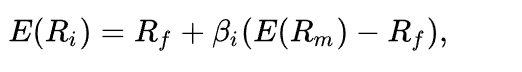
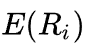 Ожидаемая ставка доходности актива.
Ожидаемая ставка доходности актива.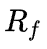 Безрисковая ставка доходности (как правило, ОФЗ).
Безрисковая ставка доходности (как правило, ОФЗ).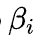 Бета-коэффициент, мера рыночного риска актива.
Бета-коэффициент, мера рыночного риска актива.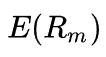 Ожидаемая доходность рыночного портфеля (для простоты расчета чаще всего берется доходность индекса).
Ожидаемая доходность рыночного портфеля (для простоты расчета чаще всего берется доходность индекса).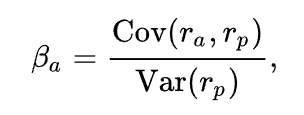
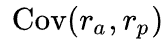 Ковариация доходностей актива, для которого рассчитывается коэффициент бета с доходностью рыночного портфеля (эталона).
Ковариация доходностей актива, для которого рассчитывается коэффициент бета с доходностью рыночного портфеля (эталона).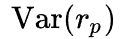 Дисперсия доходности рыночного портфеля.
Дисперсия доходности рыночного портфеля.