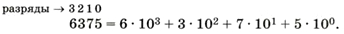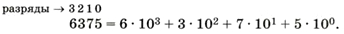Используя развернутую форму записи числа в десятичной системе счисления определите чему равен
Развёрнутая форма числа. Перевод числа из любой системы счисления в десятичную
Описание презентации по отдельным слайдам:
Описание слайда:
Тема: Развёрнутая форма числа. Перевод числа из любой системы счисления в десятичную.
Описание слайда:
Вопросы:
Что такое система счисления? Какие системы счисления вы знаете? В чём их основное отличие?
Чему равны в десятичной системе счисления следующие числа XI, LX, MDX, MCXLIII?
Чем характеризуется позиционная система счисления?
Назовите алфавит и основание 2-ной, 8-ной, 5-ной, 10-ной, 16-ной систем счисления.
Описание слайда:
Древнегреческая нумерация
В V веке до н.э. появилась алфавитная нумерация.
Описание слайда:
Славянская кириллическая нумерация
Описание слайда:
Недостатки непозиционных систем счисления
Очень трудно записать большое число;
Невозможно записать дробное и отрицательное число;
Сложно выполнять арифметические операции, так как не существует алгоритмов их выполнения.
Описание слайда:
Достоинства позиционных систем счисления
Простота выполнения арифметических операций;
Легко записываются большие числа;
Возможно множество позиционных систем, но необходимо помнить: за основание системы счисления можно принять любое число не меньшее 2.
Описание слайда:
Любое целое число можно представить в виде суммы разрядных слагаемых – единиц, десятков, сотен, тысяч и т.д.
1652 = 11 000 + 6100 + 510 + 21
1652=1*103 +6*102+5*101+2*100
Развёрнутая форма записи числа
1652-свёрнутая форма записи числа
Развёрнутая форма числа
а0=1
Описание слайда:
Задание: Записать числа в развёрнутом виде.
10012
1456
21358
1A516
27,48
101012=1*24+0*23+1*22+0*21+1*20
Описание слайда:
Перевод чисел в десятичную систему
Записать число в развёрнутом виде;
Провести вычисления.
Описание слайда:
О какой системе счисления идёт речь в данном стихотворении?
Ей было 1100 лет.
Она в 101 класс ходила.
В портфеле по 100 книг носила.
Всё это правда, а не бред.
И 10 тёмно-синих глаз
Оглядывали мир привычно.
Но станет всё совсем обычно
Когда поймёте наш рассказ.
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Курс повышения квалификации
Охрана труда
Курс профессиональной переподготовки
Библиотечно-библиографические и информационные знания в педагогическом процессе
Курс профессиональной переподготовки
Охрана труда
Ищем педагогов в команду «Инфоурок»
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
также Вы можете выбрать тип материала:
Общая информация
Похожие материалы
Средства и технологии создания и преобразования информационных объектов
Компьютерные вирусы и антивирусные программы. Типы компьютерных вирусов
Современные способы и средства защиты информации
Безопасный интернет
Логические основы устройства компьютера. Сумматор двоичных чисел. Триггер
Язык программирования Pascal. Работа со строками
Истина заключается в том, что истины не существует
Научно-техническая революция
Не нашли то что искали?
Воспользуйтесь поиском по нашей базе из
5422873 материала.
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Путин поручил не считать выплаты за классное руководство в средней зарплате
Время чтения: 1 минута
Ученые изучили проблемы родителей, чьи дети учатся в госпитальных школах
Время чтения: 5 минут
Российские юниоры завоевали 6 медалей на Международной научной олимпиаде
Время чтения: 2 минуты
Минздрав включил вакцинацию подростков от ковида в календарь прививок
Время чтения: 1 минута
В Минпросвещения рассказали о формате обучения школьников после праздников
Время чтения: 1 минута
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Содержание урока
Позиционные системы счисления
Позиционные системы счисления
Позиционная система счисления — это такая система, в которой значение цифры полностью определяется её местом (позицией) в записи числа.
Пример позиционной системы счисления — привычная нам десятичная система. В числе 6375 цифра 6 обозначает тысячи (6000), цифра 3 — сотни (300), цифра 7 — десятки (70), а цифра 5 — единицы:
6375 = 6 • 1000 + 3 • 100 + 7 • 10 + 5 • 1
Алфавит системы счисления — это используемый в ней набор цифр.
Основание системы счисления — это количество цифр в алфавите (мощность алфавита).
В десятичной системе основание — 10, алфавит состоит из 10 цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9. Число 10, вероятно, было выбрано потому, что люди сначала использовали для счета свои 10 пальцев на руках.
Разряд — это позиция цифры в записи числа. Разряды в записи целых чисел нумеруются с нуля справа налево.
В числе 6375 цифра 6 стоит в третьем разряде (тысячи, 10 3 ), 3 — во втором разряде (сотни, 10 2 ), 7 — в первом (десятки, 10 1 ), а 5 — в нулевом (единицы, 10 0 ). Поэтому
Это развёрнутая форма записи числа. Не забывайте, что любое число (кроме нуля!) в нулевой степени равно 1.
Запишите числа 158 и 1879 в развёрнутой форме.
Используя развёрнутую форму записи числа в десятичной системе счисления, определите, чему равен:
а) остаток от деления некоторого числа на 10;
б) остаток от деления некоторого числа на 100.
Как определить, что число без остатка делится на 10? На 100?
Все другие позиционные системы счисления, которые мы будем изучать, устроены так же, как и десятичная система, изменяется только основание. В первую очередь нас будет интересовать двоичная система (система с основанием 2). Она позволяет записать любое число в двоичном коде, который используется в компьютерах для хранения всех данных.
Мы познакомимся также с восьмеричной и шестнадцатеричной системами, которые применяют для сжатой записи двоичных кодов.
Как вы думаете, какие основания имеют восьмеричная и шестнадцатеричная системы счисления?
Какой алфавит может быть у двоичной системы счисления? У восьмеричной системы? У шестнадцатеричной системы?
Если число записано в позиционной системе с основанием, не равным 10, это основание записывают справа от числа как нижний индекс. Например, число 101102 записано в двоичной системе, 1235 — в пятеричной, а 7458 — в восьмеричной, а 29616 — в шестнадцатеричной.
Найдите числа, которые записаны неправильно.
Представьте число 23 в развёрнутой форме через степени числа 2. Как теперь можно записать это число в двоичной системе счисления?
Для чисел 12, 75, 150 и 513 определите старшую степень числа в развёрнутой форме через степени числа 2. Как вы рассуждали?
Сформулируйте правило перевода числа из любой позиционной системы в десятичную.
Если основание системы счисления неизвестно, всё равно можно записать число в развёрнутой форме, обозначив основание как неизвестную величину х:
В последнем равенстве учтено, что х 1 = х и х 0 = 1.
Задача. В некоторой системе счисления число 58 записывается как 46x. Определите основание х этой системы счисления.
Решение. Поскольку в записи числа 46x. есть цифра 6, можно сразу сказать, что х > 6 (в алфавитах систем счисления с меньшим основанием цифры 6 нет). Представим число 46x в развёрнутой форме: 46x = 4 • х + 6, и приравняем к 58:
4 • х + 6 = 58.
Решив это уравнение, получаем: х = 13.
В некоторой системе счисления число 45 записывается как 63x. Определите основание х этой системы счисления.
Найдите основание х системы счисления, в которой выполняется равенство 16x + 33x = 52x.
Как записывается наименьшее трёхзначное число в системе счисления с основанием х? Чему оно равно в десятичной системе?
Как записывается наибольшее трёхзначное число в системе счисления с основанием х? Чему оно равно в десятичной системе?
Найдите наименьшее основание системы счисления, в которой запись числа 30 имеет 3 значащих разряда.
Вася составил задачу: «В какой системе счисления число 15 записывается как 25x?». Есть ли у неё решение? Обоснуйте ответ.
Следующая страница 
Выводы. Интеллект-карта
Cкачать материалы урока
Перевод чисел из одной системы счисления в другую
Данный конвертер переводит числа между наиболее популярными системами счисления: десятичной, двоичной, восьмеричной, шестнадцатеричной.
Существуют и другие системы счисления, но мы не стали включать их в конвертер из-за низкой популярности.
Для указания системы счисления при записи числа используется нижний индекс, который ставится после числа:
20010 = 110010002 = 3108 = C816
Кратко об основных системах счисления
Десятичная система счисления. Используется в повседневной жизни и является самой распространенной. Все числа, которые нас окружают представлены в этой системе. В каждом разряде такого числа может использоваться только одна цифра от 0 до 9.
Двоичная система счисления. Используется в вычислительной технике. Для записи числа используются цифры 0 и 1.
Восьмеричная система счисления. Также иногда применяется в цифровой технике. Для записи числа используются цифры от 0 до 7.
Перевод в десятичную систему счисления
Перевод из десятичной системы счисления в другие
Делим десятичное число на основание системы, в которую хотим перевести и записываем остатки от деления. Запишем полученные остатки в обратном порядке и получим искомое число.
Переведем число 37510 в восьмеричную систему:
Перевод из двоичной системы в восьмеричную
Так же как и в первом способе разбиваем число на группы. Но вместо преобразований в скобках просто заменим полученные группы (триады) на соответствующие цифры восьмеричной системы, используя таблицу триад:
Перевод из двоичной системы в шестнадцатеричную
Также как и в первом способе разбиваем число на группы по 4 цифры. Заменим полученные группы (тетрады) на соответствующие цифры шестнадцатеричной системы, используя таблицу тетрад:
| Тетрада | 0000 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Цифра | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
Перевод из восьмеричной системы в двоичную
Каждый разряд восьмеричного числа будем делить на 2 и записывать остатки в обратном порядке, формируя группы по 3 разряда двоичного числа. Если в группе получилось меньше 3 разрядов, тогда дополняем нулями. Записываем все группы по порядку, отбрасываем ведущие нули, если имеются, и получаем двоичное число.
Используем таблицу триад:
Каждую цифру исходного восьмеричного числа заменяется на соответствующие триады. Ведущие нули самой первой триады отбрасываются.
Перевод из шестнадцатеричной системы в двоичную
Аналогично переводу из восьмеричной в двоичную, только группы по 4 разряда.
Используем таблицу тетрад:
| Цифра | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Тетрада | 0000 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 |
Каждую цифру исходного числа заменяется на соответствующие тетрады. Ведущие нули самой первой тетрады отбрасываются.
Перевод из восьмеричной системы в шестнадцатеричную и наоборот
Такую конвертацию можно осуществить через промежуточное десятичное или двоичное число. То есть исходное число сначала перевести в десятичное (или двоичное), и затем полученный результат перевести в конечную систему счисления.
Урок 4
§7. Системы счисления
Содержание урока
Позиционные системы счисления
Позиционные системы счисления
Позиционная система счисления — это такая система, в которой значение цифры полностью определяется её местом (позицией) в записи числа.
Пример позиционной системы счисления — привычная нам десятичная система. В числе 6375 цифра 6 обозначает тысячи (6000), цифра 3 — сотни (300), цифра 7 — десятки (70), а цифра 5 — единицы:
6375 = 6 • 1000 + 3 • 100 + 7 • 10 + 5 • 1
Алфавит системы счисления — это используемый в ней набор цифр.
Основание системы счисления — это количество цифр в алфавите (мощность алфавита).
В десятичной системе основание — 10, алфавит состоит из 10 цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9. Число 10, вероятно, было выбрано потому, что люди сначала использовали для счета свои 10 пальцев на руках.
Разряд — это позиция цифры в записи числа. Разряды в записи целых чисел нумеруются с нуля справа налево.
В числе 6375 цифра 6 стоит в третьем разряде (тысячи, 10 3 ), 3 — во втором разряде (сотни, 10 2 ), 7 — в первом (десятки, 10 1 ), а 5 — в нулевом (единицы, 10 0 ). Поэтому
Это развёрнутая форма записи числа. Не забывайте, что любое число (кроме нуля!) в нулевой степени равно 1.
Запишите числа 158 и 1879 в развёрнутой форме.
Используя развёрнутую форму записи числа в десятичной системе счисления, определите, чему равен:
а) остаток от деления некоторого числа на 10;
б) остаток от деления некоторого числа на 100.
Как определить, что число без остатка делится на 10? На 100?
Все другие позиционные системы счисления, которые мы будем изучать, устроены так же, как и десятичная система, изменяется только основание. В первую очередь нас будет интересовать двоичная система (система с основанием 2). Она позволяет записать любое число в двоичном коде, который используется в компьютерах для хранения всех данных.
Мы познакомимся также с восьмеричной и шестнадцатеричной системами, которые применяют для сжатой записи двоичных кодов.
Как вы думаете, какие основания имеют восьмеричная и шестнадцатеричная системы счисления?
Какой алфавит может быть у двоичной системы счисления? У восьмеричной системы? У шестнадцатеричной системы?
Если число записано в позиционной системе с основанием, не равным 10, это основание записывают справа от числа как нижний индекс. Например, число 101102 записано в двоичной системе, 1235 — в пятеричной, а 7458 — в восьмеричной, а 29616 — в шестнадцатеричной.
Найдите числа, которые записаны неправильно.
Представьте число 23 в развёрнутой форме через степени числа 2. Как теперь можно записать это число в двоичной системе счисления?
Для чисел 12, 75, 150 и 513 определите старшую степень числа в развёрнутой форме через степени числа 2. Как вы рассуждали?
Сформулируйте правило перевода числа из любой позиционной системы в десятичную.
Если основание системы счисления неизвестно, всё равно можно записать число в развёрнутой форме, обозначив основание как неизвестную величину х:
В последнем равенстве учтено, что х 1 = х и х 0 = 1.
Задача. В некоторой системе счисления число 58 записывается как 46x. Определите основание х этой системы счисления.
Решение. Поскольку в записи числа 46x. есть цифра 6, можно сразу сказать, что х > 6 (в алфавитах систем счисления с меньшим основанием цифры 6 нет). Представим число 46x в развёрнутой форме: 46x = 4 • х + 6, и приравняем к 58:
4 • х + 6 = 58.
Решив это уравнение, получаем: х = 13.
В некоторой системе счисления число 45 записывается как 63x. Определите основание х этой системы счисления.
Найдите основание х системы счисления, в которой выполняется равенство 16x + 33x = 52x.
Как записывается наименьшее трёхзначное число в системе счисления с основанием х? Чему оно равно в десятичной системе?
Как записывается наибольшее трёхзначное число в системе счисления с основанием х? Чему оно равно в десятичной системе?
Найдите наименьшее основание системы счисления, в которой запись числа 30 имеет 3 значащих разряда.
Вася составил задачу: «В какой системе счисления число 15 записывается как 25x?». Есть ли у неё решение? Обоснуйте ответ.
Следующая страница Выводы. Интеллект-карта
Cкачать материалы урока
Урок по информатике.Решение задач по теме:Системы счисления.
Решение задач по теме «Системы счисления»
Системой счисления называется совокупность правил наименования и изображения чисел с помощью конечного набора символов, называемых цифрами.
Системы счисления бывают непозиционные и позиционные.
Система счисления называется непозиционной, если значение цифры в записи числа не зависит от позиции, которую она занимает в последовательности цифр, изображающей число. Примеры непозиционных систем счисления: римская, древнегреческая и др.
Система счисления называется позиционной, если значение цифры в записи числа зависит от позиции, которую она занимает в последовательности цифр, изображающей число. Примеры позиционных систем счисления: десятичная, двоичная, восьмеричная, шестнадцатеричная и др.
В позиционных системах счисления основание системы счисления – это количество цифр, используемых в записи числа. В таблице собраны примеры нескольких систем счисления с указанием их основания и алфавита.
В следующей таблице приведены первые 17 числе нескольких систем счисления:
Обратите внимание, что при последовательном счете, начиная с нуля, в любой системе обязательно наступает момент, когда число становится двузначным и обозначается как «10». Появление двух знаков в изображении числа означает, что кончились знаки алфавита данной системы счисления и приходится использовать комбинацию из двух цифр.
Развернутая форма записи чисел
q – основание системы счисления,
ai – цифры данной системы счисления ( an -2 ; an -1 и др.),
n – число разрядов целой части числа,
Пример 1. Записать в развернутом виде число А10 = 5124,23
Пример 2. Записать в развернутом виде число А8 = 327,14
Свернутой формой записи чисел называется запись в виде
Перевод из десятичной системы в другие системы счисления
Алгоритм перевода целых чисел из десятичной системы счисления в любую другую.
1. Последовательно выполнять деление данного числа и получаемых целых частных на основание новой системы счисления до тех пор, пока не получится частное, меньше делителя.
3. Составить число в новой системе счисления, записывая его, начиная с последнего частного.
Например, для перевода из десятичной системы в двоичную, делят на 2; для перевода в восьмеричную – на 8 и т.д.
Таким образом, 17510 à 101011112
Таким образом, 17510 à 2578
Число 15 в шестнадцатеричной системе записывается как « F », а число 10 – как «А». Таким образом, 17510 à AF 16
Дробную часть числа, если таковая имеется, переводят по другому алгоритму.
1. Последовательно умножить данное число и получаемые дробные части произведения на основание новой системы счисления до тех пор, пока дробная часть произведения не станет равна нулю или не будет достигнута требуемая точность представления числа.
2. Полученные целые части произведений, являющиеся цифрами числа в новой системе счисления, привести в соответствие с алфавитом новой системы счисления.
3. Составить дробную часть числа в новой системе счисления, начиная с целой части первого произведения.
0,
Пример 8. 0,6562510 à x8
Пример 9. 0,6562510 à x16
0,
Этот перевод можно продолжать бесконечно. В этом случае деление производим до тех пор, пока не получим нужную точность представления числа.
Для перевода произвольных чисел, т.е. содержащих целую и дробную части, осуществляется в два этапа. Отдельно переводится целая часть, отдельно – дробная. В итоговой записи полученного числа целая часть отделяется от дробной запятой.
Перевод чисел из любой системы счисления в десятичную
Алгоритм перевода чисел из любой системы счисления в десятичную.
1. Представить число в развернутой записи. При этом основание системы счисления должно быть представлено в десятичной системе счисления.
2. Найти сумму ряда. Полученное число является значением числа в десятичной системе счисления.
2. Найдем сумму ряда: 7*0,125 + 0,0625 = 0,937510.
Перевод чисел из двоичной системы счисления в систему счисления с основанием
q = 2 n .
2. Если в крайней левой в целой части и/или в крайней правой в дробной части группе окажется меньше n разрядов, то их надо дополнить нулями до нужного числа разрядов.
Перевод чисел из системы счисления с основанием q = 2 n в двоичную систему счисления.
Алгоритм перевода чисел из системы счисления с основанием q = 2 n в двоичную систему счисления.
Таблица сложения двоичных чисел
1 означает перенос в следующий разряд
Таблица вычитания двоичных чисел
1 означает заем из старшего разряда
Таблица умножения двоичных чисел
Обратите внимание на то, что 1 +1 +1 = 1 + перенос 1 в следующий разряд
Примеры из заданий ЕГЭ
Переведем все данные нам числа в десятичную систему счисления. Проще будет сравнивать числа.
A = 9 D 16 = 9*16 1 + D *16 0 = 144 + 13*1 = 15710.
В = 2378 = 2*8 2 + 3*8 1 + 7*8 0 = 128 + 24 + 7 = 15910.
Далее переведем 15810 в двоичную систему счисления. 15810 = 100111102. Правильный ответ 2.
Результат представьте в двоичном виде.
Переведем число Y = 135 8 в двоичную систему счисления.
1 0 0 1 0 1 0 0 Правильный ответ 4.
В системе счисления с некоторым основанием десятичное число 49 записывается в виде 100. Укажите это основание.
Допустим, что основание системы равно х, тогда составим развернутую форму записи числа:
По условию задачи х 2 = 4910. Найдем х:
Можно выполнить проверку. Переведем число 4910 в 7-ричную систему счисления:
4. Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 17 оканчивается на 2.
3. Задание B 3 (Информатика: ЕГЭ-2009: Самые новые издания/ авт.-сост. О.В. Ярцева, Е.Н. Цикина. – М.: АСТ: Астрель, 2009)
В саду 100 q фруктовых деревьев. Из них 33 q яблони, 22 q груши, 16 q слив и 5 q вишен. В какой системе счисления посчитаны деревья?
Воспользуемся развернутой формой записи чисел:
(3* q 1 + 3* q 0 ) + (2* q 1 + 2* q 0 ) + (1* q 1 + 6* q 0 ) + 5* q 0 = 1* q 2 + 0* q 1 + 0* q 0 ;
3 q + 3 + 2 q + 2 + q + 6 + 5 = q 2 ;
q 2 – 6 q – 16 = 0 Þ q = 8. Проверку выполните самостоятельно.
4. Задание B 3 (Информатика: ЕГЭ-2009: Самые новые издания/ авт.-сост. О.В. Ярцева, Е.Н. Цикина. – М.: АСТ: Астрель, 2009)
(Информатика: ЕГЭ-2009: Самые новые издания/ авт.-сост. О.В. Ярцева, Е.Н. Цикина. – М.: АСТ: Астрель, 2009)
Укажите через запятую в порядке возрастания все десятичные числа, не превосходящие 41, запись которых в системе счисления с основанием 3, оканчивается на 12.
В интервале от 4 до 41 выберем те числа, которые при делении на 3 дают остаток 2. Это 5, 8, 11, 17, 20, 23, 26, 29, 32, 35, 38, 41.
Далее из полученных чисел выберем, у которых частное от их деления 3, при делении на 3 еще раз, дает остаток 1.
13 : 3 = 4 (ост. 1) Þ 41 – искомое число.
12 : 3 = 4 (ост. 0) – при переводе числа 38 в 3-ричную систему счисления получим число, оканчивающееся на 10, а не на 12 как нам требуется по условию задания. Не забудьте в ответе выписать полученные числа в порядке возрастания!
Ответ: 5, 14, 23, 32, 41.
5. Задание B 3 (Информатика: ЕГЭ-2009: Самые новые издания/ авт.-сост. О.В. Ярцева, Е.Н. Цикина. – М.: АСТ: Астрель, 2009)
Сумму восьмеричных чисел 17 + 170 + 1 700 + … + 1 700 000 перевели в шестнадцатеричную систему счисления. Найдите в записи числа, равного этой сумме, третью цифру слева.
Решим задание «в лоб». Найдем сумму восьмеричных чисел 17 + 170+1 700+17 000 + 170 000 + 1 700 000.
Задания для самостоятельного решения.
2. Какое из неравенств выполняется для чисел А = 1648, В = А316, С = 22004?
3. Сколько значащих нулей содержится в двоичной записи суммы чисел а = 1058 и
b = С616?
4. Сколько единиц содержится в двоичной записи суммы чисел а = 3А16 и
b = 738?
3. В системе счисления с некоторым основанием число 12 записывается как 110. Укажите это основание.
4. Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 15 оканчивается на 3.
Подсказка. Основание системы должно быть больше 3.
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс повышения квалификации
Педагогическая деятельность в контексте профессионального стандарта педагога и ФГОС
Курс повышения квалификации
Современные педтехнологии в деятельности учителя
Ищем педагогов в команду «Инфоурок»
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
также Вы можете выбрать тип материала:
Краткое описание документа:
Решение задач. Системы счисления. Общие сведения. Перевод из двоичной в десятичную систему счисления и обратно. Развернутая форма записи чисел. Перевод из десятичной системы в другие системы счисления. Перевод чисел из любой системы счисления в десятичную. q = 2n. q = 2n в двоичную систему счисления.
Общая информация
Похожие материалы
Реферат по имитационному моделированию на тему Моделирование в среде Unity.
Презентация по системе Octave
Конспект урока на тему “Информационная безопасность”
Урок информатики «Формулы в языке Паскаль» на английском языке
Учебно методическая разработка
Учебные среды программирования: Alice, Etoys, Scratch
Учебные среды программирования: Alice, Etoys, Scratch
Презентация.Моделирование циклических процессов в расширении языка Pascal
Не нашли то что искали?
Воспользуйтесь поиском по нашей базе из
5422873 материала.
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
В Минпросвещения рассказали о формате обучения школьников после праздников
Время чтения: 1 минута
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Большинство родителей в России удовлетворены качеством образования в детсадах
Время чтения: 2 минуты
В российских школах могут появиться «службы примирения»
Время чтения: 1 минута
При засыпании человеческий мозг может решать сложные задачи
Время чтения: 1 минута
Путин поручил не считать выплаты за классное руководство в средней зарплате
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.