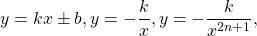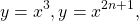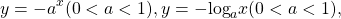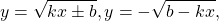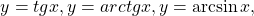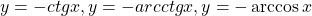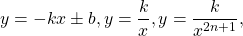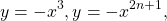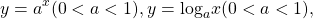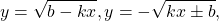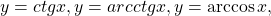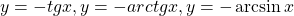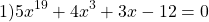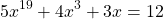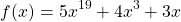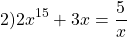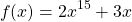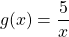Используя свойство монотонности функции докажите что уравнение имеет единственный корень

Решение уравнений с помощью монотонности функций

Решение уравнений с помощью монотонности функций позволяет быстро и просто найти корень уравнения (либо доказать, что уравнение корней не имеет).

Использование возрастания и убывания функций при решении уравнений опирается на следующие теоремы.

1) Если на некотором промежутке функция f(x) возрастает (или убывает), то уравнение f(x)=a на этом промежутке имеет единственный корень либо не имеет корней (a — постоянная величина (число)).

2) Если на некотором промежутке функция f(x) возрастает, а функция g(x) убывает (либо наоборот), то уравнение f(x)=g(x) на этом промежутке имеет единственный корень либо не имеет корней.

Доказав, что уравнение имеет на промежутке не более чем один корень, можно попытаться определить его подбором.

Если функция имеет несколько промежутков возрастания и убывания, каждый из них следует рассмотреть отдельно.

Сумма возрастающих функций — возрастающая функция. Сумма убывающих функций — убывающая функция.

Прибавление или вычитание постоянной величины не влияет на монотонность функции. Если к возрастающей функции прибавить (или вычесть) постоянную величину, получим возрастающую функцию. Если к убывающей функции прибавить (или вычесть) постоянную величину, получим убывающую функцию.

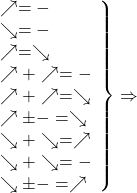
Таким образом, использование монотонности функций при решении уравнений схематически можно изобразить так:

то уравнение имеет единственный корень или не имеет корней.

Разумеется, количество слагаемых может быть больше двух.

Некоторые функции, возрастающие на всей области определения либо на каждом из промежутков, из объединения которых состоит область определения (k>0, b≥0, n — целое):

1),y = <\log _a>x(a > 1),\]» title=»Rendered by QuickLaTeX.com»/>

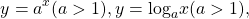
Некоторые функции, убывающие на всей области определения либо на каждом из промежутков, из объединения которых состоит область определения:

Примеры решения уравнений с помощью использования монотонности функций.

Перепишем уравнение в виде

является возрастающей (как сумма возрастающих функций). Следовательно, уравнение имеет не более одного корня. Подбором находим, что x=1.

На промежутке (-∞;0) функция

Аналогично, на промежутке (0:∞)

— убывает, следовательно, уравнение имеет не более одного корня. Подбором находим x=1.

В алгебре решение уравнений с применением возрастания и убывания функций чаше всего используется при решении иррациональных, логарифмических, показательных уравнений. Полезно взять на вооружение этот удобный и быстрый способ.

2 комментария

Добрый день. Вот это схематическое изображение монотонности очень интересно, но там не все понятно. Что вы подразумеваете под знаками равно и минус? И вот это: сумма убывающих_возрастающая? Буду благодарна комментариям

Елена, «=» — знак равенства между левой и правой частями уравнения.
Сумма убывающих функций — убывающая функция. Соответственно, одна часть уравнения — убывающая функция, а другая — возрастающая, то применима вторая теорема.
Аналогично, сумма возрастающих функций есть возрастающая функция. Если с одной стороны — возрастающая функция, с другой — убывающая, можем применить первую теорему.
Если к монотонно возрастающей функции прибавить число (или вычесть), то это никак не повлияет на её монотонность (это наглядно можно продемонстрировать графически: график функции y=f(x)±b получен из графика y=f(x) параллельным переносом на b единиц вверх или вниз вдоль оси Oy). Поэтому, если в одной части уравнения — монотонно возрастающая функция ± число, а в другой — монотонно убывающая функция, можем применить теорему два. И т.д.

Источник

Использование свойства монотонности функции при решении уравнений

Разделы: Математика

Оборудование: карточки с заданиями для каждого ученика.

Организационный момент: сообщить тему урока, сформулировать цели урока.

Проводится фронтальный опрос учащихся:

Свойство 1. Если y=g(x) – монотонно возрастает на промежутке I и y=f(x) – монотонно возрастает на промежутке I, то y=g(x)+f(x) – монотонно возрастает на промежутке I.

Свойство 2. Если y=f(x) возрастает (убывает) на промежутке I, то уравнение f(x)=a имеет на I не более одного корня.

Свойство 3. Если y=f(x) возрастает на I, а y=g(x) убывает на I, то уравнение f(x)=g(x), имеет не более одного корня.

II. Решение уравнений

( Этот этап урока проходит в форме беседы учителя с учениками. Ученики, основываясь на прошлом опыте решения уравнений, предлагают свои решения. Учитель показывает им более рациональные способы решения этих уравнений)

Пример 1. Решите уравнение: x 5 +x 3 +2x-4=0.

Тогда уравнение f(x)=0 имеет не более одного корня. Испытывая делители свободного члена, находим, что x=1.

Пример 2. Решите уравнение .

Решение: Функция — возрастает на своей области определения, как сумма двух возрастающих функций и . Следовательно, уравнение f(x)=2 имеет не больше одного корня на [-1,45; 26]. Непосредственно проверкой убеждаемся что f(1)=0. Уравнение решено: мы нашли корень и доказали, что других корней нет.

Учащимся предлагается решить это уравнение дома с помощью возведения в квадрат лавой и правой частей уравнения, и убедится что решение будет очень громоздким.

Пример 3. Решите уравнение log₂(x+2)=1-x.

Решение: Функция y=log₂(x+2) – возрастает на (-2; +). Функция y=1-x убывает на R. Тогда уравнение log₂(x+2)=1-x имеет единственное решение при x (-2; +).

Непосредственно проверкой убедимся, что x=0 является корнем этого уравнения.

Каким еще способом можно решить это уравнение? (графически)

Пример 4. Определите число корней уравнения .

Решение: Рассмотрим функцию эта функция возрастает на области определения , тогда , т.е. f(x)4, где x D(f). Значит множеством значений функции f(x) является промежуток [+4;+).

Т.е. при a4 уравнение имеет единственное решение, при a 5 +3x=4.

IV. К доске приглашаются ученики из обоих вариантов и показывают решение уравнений

V. Подведение итогов урока и выставление оценок

[1] В.В. Локоть. Применение свойств функций, преобразование неравенств // АРКТИ, Москва 2007 г.

[2] Ю.Н. Макарычев. Дополнительные главы к школьному учебнику 9 класс // Просвещение, 1998 г.

[3] И.Я. Виленкин. Алгебра и математический анализ 10 // Просвещение, 1998 г.

[4] Е.Д. Кулакин. 3000 конкурсных задач по математике // Москва 2002 г.

Источник

Использование свойства монотонности функции при решении уравнений

Джамирова МархабоАмоновна учитель математики

Муниципальное бюджетное общеобразовательное учреждение«Плодовская средняя общеобразовательная школа»Бахчисарайского района

Алгебра и начала математического анализа

Учебник для 11 кл. общеобразовательных учреждений: базовый и профильный уровни / С.М. Никольский, М.К. Потапов, Н.Н. Решетников, А.В. Шевкин. – 12-е изд. – М.: Просвещение, 2014

Тема урока: Использование свойства монотонности функции при решении уравнений

Всё чаще и чаще «линия уравнений» в школьном курсе математики пересекается с «функциональной линией». В задачниках, в материалах ЕГЭ, в задачах, представленных на вступительных экзаменах в ВУЗы, предлагаются нестандартные уравнения, при решении которых необходимо использовать свойства функций

В математике, как известно, выше всего ценится не просто верное решение, но и наиболее короткое из возможных, как говорят сами математики, более рациональное.

Как найти такое решение? Что для этого необходимо знать? Чем владеть?

Не всякое уравнение (неравенство) в результате преобразований или с помощью удачной замены переменной может быть сведено к уравнению (неравенству) того или иного стандартного вида, для которого существует определенный алгоритм решения. В таких случаях иногда оказывается полезным использовать другие методы решения (метод монотонности функции, ограниченности, использование области допустимых значений, неотрицательности и т.д.). Решение уравнений с помощью монотонности функций позволяет быстро и просто найти корень уравнения (либо доказать, что уравнение корней не имеет).

Технологическая карта урока математики

Учитель математики Джамирова М.А.

МБОУ «Плодовская СОШ»,с Плодовое.

Алгебра и начала математического анализа

11 класс. Учебник для 11класса, Никольский С.М.

Использование монотонности функции при решении уравнений

Урок усвоения новых знаний

Развитие системы знаний об уравнениях и неравенствах, при решении которых применяется монотонность функции

Развитие вычислительных навыковучащихся, формирование умения проводить анализ, обобщать, делать выводы.

Воспитание умения вести диалог, самостоятельности мышления, интереса к предмету.

доска, компьютеры, раздаточный материал

Формы организации деятельности обучающихся

Индивидуальная работа; работа в парах; фронтальная работа

Формирование навыков решения уравнений с помощью использования свойства монотоннности функции. Умение применять математические знания при выполнении практических заданий.

Умение выдвигать гипотезу, отстаивать или опровергать ее. Умение находить в источниках необходимую информациюдля решения математических проблем.

Умение записывать ход решения по образцу. Умение грамотно излагать свои мысли, дополнять и исправлять ответы других учащихся, находить другие способы решения.

На доске записаны дата, тема урока и задача на решение уравнения.

Учитель приветствует класс, создает позитивный настрой на урок. Раздает листы самооценки. В ходе урока каждый заполняет лист самооценки и сдает в конце учителю. Приложение 1.

Проверяется наличие и выполнение домашнего задания.

Задача: решить уравнение

: может ли кто-нибудь решить это уравнение?

Я уверена, что к концу урока большинство из вас научится решать такие уравнения. Для этого в уравнении необходимо увидеть его структуру и использовать свойства функции, входящих в данное уравнение. Из множества свойств функций мы будем использовать сегодня монотонность. Это и является целью урока.

Приветствуют учителя, настраиваются на работу, концентрируют внимание, получают позитивный заряд

Регулятивные: способность регулировать свои действия, прогнозиро-вать деятель-ность на уроке

3.Актуализация опорных знаний

А сейчас проведем лотерею. Приглашаю любых 5 учащихся (они вытягивают карточку и выбирают в помощники одного из учащихся). Отвечаем на вопросы карточки сразу (если первый ученик не может ответить, помогает второй). Приложение 2.

Устно повторяют свойства функций и применяют знания на практике.

Регулятивные: способность провести самооценку

6. Открытие нового знания. Исследование и решение проблемы

Использо-вание областей существо-вания функций

При ответе на вопросы лотереи вы уже упоминали о возрастающих и убывающих функциях. Давайте вспомним определение монотонных функций (возрастающих и убывающих)

Решение: – Можем ли мы угадать хоть один корень?

Итак, сформулируем следующее утверждение и запись в тетрадь:

Пусть функция возрастает на промежутке М, а функция убывает на этом промежутке. Тогда уравнение имеет на промежутке М не более одного корня .Например:

G ( x )=- x +5 – убывающая, тогда исходное уравнение на промежутке от 0 до +бесконечности метет не более одного корня, подбираем, и это x =1

Применим эти утверждение на практике.Работаем в Яклассе, у каждого уже имеется практическое задание, которое необходимо решить По окончанию выполнения задания,ребята в лист самооценки выставляют балы за правильно решенное уравнение). Приложение 3.

Этап 3. А теперь перейдем к более сложным уравнениям. В таких случаях лучше применять следующее утверждение:

Пусть область определения функции есть промежуток М, и пусть эта функция непрерывна и строго монотонна (т.е. возрастает или убывает) на этом промежутке. Тогда уравнение равносильно системе

Этап 4. Работа в группах.

Можно,корень уравнения: х = 1.

Личностные: осознание своих возмож-ностей; анализируя и вспоминания теорию, нахо-дятнеобходи-муюинформа-цию для реше-нияуравнений и неравенств.

Регулятивные: целеполагание, прогнозирова-ние

Устное сообщение учителя, учащихся

— можно ли применять монотонность при решении уравнений?

— эффективно ли применение монотонности при решении уравнений? (да, некоторые уравнения просто не смогли бы решить другими методами)

— Что нового вы узнали на этом уроке?

— Какие задачи из предложенных вам понравилось решать?

— Чувствуете ли вы уверенность в данный момент перед нестандартными уравнениями?

Подсчет балов и сдача листов самооценки, выставлениеи краткий комментарий отметок.

Отвечают на вопросы, получают оценки по результатам выполненной работы

Личностные: умение провес-ти самооценку и организовать взаимооценку.

Регулятивные: построение ло-гическойце-почки рассуж-дений и дока-зательство.

Информа-ция о до-машнем задании

Учитель информирует о домашнем задании:для сильных учащихся решить задание согласно утверждения3:

_{, для слабо мотивированных- из учебника}

Источник

Поэтому данное уравнение либо не имеет корней, либо имеет один единственный корень.

При каком значении параметра а уравнение ах = 3а + х имеет единственный корень?

При каком значении параметра а уравнение ах = 3а + х имеет единственный корень?

В каком случае уравнение ах = b имеет единственный корень?

В каком случае уравнение ах = b имеет единственный корень?

При каком условии уравнение 0у = 3 имеет единственный корень?

При каком условии уравнение 0у = 3 имеет единственный корень.

При каких значениях k уравнение имеет единственный корень?

При каких значениях k уравнение имеет единственный корень.

Помогите пожалуйста, очень срочно надо?

Помогите пожалуйста, очень срочно надо!

Найдите корни уравнения, воспользовавшись свойством монотонности функций : 0.

Найдите все значения а, при каждом из которых уравнение ax + имеет единственный корень?

Найдите все значения а, при каждом из которых уравнение ax + имеет единственный корень.

Используя свойства монотонных функций, решите уравнения?

Используя свойства монотонных функций, решите уравнения.

А) x ^ 6 + 2x ^ 4 + 3x ^ 2 = 6 б) квадратный корень из x ^ 2 + 5 + квадратный корень из 2x ^ 2 + 1 = 6.

Источник

Использование монотонности функции.

ФГБОУ ВО «ИРКУТСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»

Заочная физико-математическая школа

МАТЕМАТИКА

ЗАДАНИЕ № 1

Класс

Иррациональные уравнения и неравенства

Мы предполагаем, что учащиеся ЗФМШ имеют определённые навыки тождественных преобразований уравнений и неравенств, раскрытия модулей, выполнения замены переменной и т.п. А приведённые ниже краткие решения стандартных заданий помогут учащимся успешно выполнить домашнее задание.

Уравнения, в которых неизвестная величина находится под знаком радикала называются иррациональными.

К простейшим иррациональным уравнениям относятся уравнения вида:

.

Основная идея решения иррационального уравнения состоит в сведении его к рациональному алгебраическому уравнению, которое либо равносильно исходному иррациональному уравнению, либо является его следствием. При решении иррациональных уравнений речь всегда идет об отыскании действительных корней. Область допустимых значений иррационального уравнения состоит из тех значений неизвестных, при которых неотрицательными являются все выражения, стоящие под знаком радикала четной степени.

Иррациональные уравнения решаются, в основном возведением обеих частей уравнения в натуральную степень, то есть переходом от уравнения

(1)

. (2)

Справедливы следующие утверждения:

1) при любом уравнение (2) является следствием уравнения (1);

2) если (n – нечетное число), то уравнения (1) и (2) равносильны;

3) если (n – четное число), то уравнение (2) равносильно уравнению

, (3)

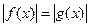
а уравнение (3) равносильно совокупности уравнений

. (4)

В частности, уравнение

(5)

равносильно совокупности уравнений (4).

Пример 1. Решить уравнение .

Решение. Запомните, что возводить в квадрат можно обе части уравнения, только если они обе неотрицательны, т.е. наше уравнение равносильно системе

откуда следует что , а корень не удовлетворяет второму неравенству. При этом грамотное решение не требует проверки.

Ответ: .

Пример 2. Решить уравнение .

Решение. Это уравнение равносильно системе

Решая первое уравнение этой системы, равносильное уравнению , получим корни и . Однако при этих значениях x не выполняется неравенство , и потому данное уравнение не имеет корней.

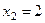
Ответ: корней нет.

Пример 3. Решить уравнение

.

Решение. Уединив первый радикал, получаем уравнение

,

Возводя обе части этого уравнения в квадрат, так как они обе положительны, получаем уравнение

,

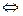
которое является следствием исходного уравнения. Возводя обе части этого уравнения в квадрат при условии, что , приходим к уравнению

.

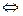
Это уравнение имеет корни , . Первый корень удовлетворяет исходному условию , а второй – не удовлетворяет.

Ответ: .

Удобным средством решения иррациональных уравнений иногда является метод введения новой переменной, или «метод замены». Метод обычно применяется в случае, если в уравнении неоднократно встречается некоторое выражение, зависящее от неизвестной величины. Тогда имеет смысл обозначить это выражение какой-нибудь новой буквой и попытаться решить уравнение сначала относительно введенной неизвестной, а потом уже найти исходную неизвестную.

Пример 4. Решите уравнение .

Ответ: 15..

Пример 5. Решить уравнение

.

Решение:Положив , получим существенно более простое иррациональное уравнение . Возведем обе части уравнения в квадрат: .

Далее последовательно получаем:

; ;

; ; , .

Проверка найденных значений их подстановка в уравнение показывает, что – корень уравнения, а – посторонний корень.

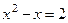
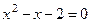
Возвращаясь к исходной переменной x, получаем уравнение , то есть квадратное уравнение , решив которое находим два корня: , . Оба корня удовлетворяют исходному уравнению.

Ответ: , .

Замена особенно полезна, если в результате достигается новое качество, например, иррациональное уравнение превращается в рациональное.

Пример 6. Решить уравнение .

Решение: Перепишем уравнение так: .

Видно, что если ввести новую переменную , то уравнение примет вид , откуда — посторонний корень и .

Из уравнения получаем , .

Ответ: , .

Пример 7. Решить уравнение .

Решение: Введем новую переменную , .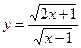

В результате исходное иррациональное уравнение принимает вид квадратного , откуда, учитывая ограничение , получаем . Решая уравнение , получаем корень .

Ответ: 2,5.

Иногда иррациональное уравнение удается решить довольно быстро, если обе его части умножить на удачно подобранную функцию. Конечно, при умножении обеих частей уравнения на некоторую функцию могут появиться посторонние решения, ими могут оказаться нули самой этой функции. Поэтому предлагаемый метод требует обязательной проверки получающихся значений.

Пример 8. Решить уравнение .

Решение: ОДЗ: . Умножим обе части уравнения на одну и ту же функцию , отметим, что в ОДЗ она положительна. Выражение называется сопряженным для выражения . Цель такого умножения ясна: использовать тот факт, что произведение двух сопряженных выражений уже не содержит радикалов.

В результате этого умножения и очевидных преобразований приходим к уравнению которое равносильно совокупности уравнений

Возводя в квадрат второе уравнение совокупности, и, с учетом ОДЗ, получим

.

Если внимательно посмотреть на неравенства последней системы, можно заметить, что пересечение множеств и пусто. Следовательно, уравнение решений не имеет. Значит, исходное уравнение имеет единственный корень .

Подстановка в исходное уравнение показывает, что – корень.

Ответ: 0.

Пример 9. Решите уравнение .

Решение: Умножив обе части уравнения на сопряженную левой части функцию: , получим

.

Приведем подобные слагаемые и получим равносильное уравнение

.

Сложив исходное уравнение и последнее, получим

Ответ: .

Некоторые иррациональные уравнения приводятся к рациональным, если увидеть полный квадрат в подкоренных выражениях.

Пример 10. Решите уравнение .

Решение: Произведем замену переменной .

Подставим замену в исходное уравнение

.

Последнее уравнение равносильно уравнению вида . Определим интервалы знакопостоянства выражений, стоящих под знаком модуля.

Составим совокупность, раскрывая модуль в каждом из указанных промежутков.

Вернемся к замене переменной .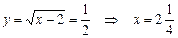

Ответ: .

Пример 11. Решите уравнение

Решение: Область допустимых значений: или

Преобразуем уравнение так, чтобы получить сумму двух полных квадратов:

Сумма двух неотрицательных выражений равна нулю тогда и только тогда, когда оба выражения равны нулю!

Поэтому наше равенство будет выполняться тогда и только тогда, когда что получается только при одном значении ,

Ответ:

Использование монотонности функции.

Пусть уравнение имеет вид: где возрастает (убывает), или где и «встречно монотонны», т.е. возрастает, а убывает или наоборот, то такое уравнение имеет не более одного корня. Если удается заметить это или привести уравнение к такому виду и при этом нетрудно угадать корень, то он и будет единственным решением данного уравнения.

Пример 12. Решите уравнение .

Решение: Это уравнение можно попытаться решить возведением в квадрат (трижды!). Однако при этом получится уравнение четвертой степени. Попробуем угадать корень. Это сделать нетрудно: 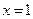. Теперь заметим, что левая часть уравнения – возрастающая функция, а правая – убывающая. Но это значит, что больше одного корня такое уравнение иметь не может. Итак, – единственный корень.

Ответ: .

Пример 13. Решить уравнение .

Решение: Как и в предыдущих примерах, несложно обнаружить, что – корень. ОДЗ

исходного уравнения – промежуток . Но теперь уже, в отличие от ранее рассмотренных задач, левая часть уравнения не задает монотонную функцию. Однако снова легко заметить, что на указанная функция возрастает, причем корень принадлежит этому промежутку. Значит, на данное уравнение имеет единственный корень. Осталось исследовать поведение функции на отрезке . Очевидно, что при , а , поэтому Следовательно, при исходное уравнение корней не имеет.

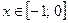
Ответ: .

Использование ОДЗ

Иногда знание ОДЗ позволяет доказать, что уравнение не имеет решений, а иногда позволяет найти решения уравнения непосредственной подстановкой чисел из ОДЗ.

Пример 14. Решить уравнение .

Решение: Конечно, это иррациональное уравнение можно решить путем традиционного возведения обеих частей в квадрат. Однако, найдя ОДЗ этого уравнения, приходим к выводу, что ОДЗ исходного уравнения – одноэлементное множество 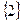. Подставив в данное уравнение, приходим к выводу, что – корень исходного уравнения.

Ответ: .

Дата добавления: 2019-01-14 ; просмотров: 269 ; Мы поможем в написании вашей работы!

Источник