Используя векторы докажите что середина отрезка bb1 лежит на прямой aa1
Применение векторов к решению задач
Просмотр содержимого документа
«Применение векторов к решению задач»
Применение векторов к решению задач
К учебнику Геометрия 7-9,
автор Л.С.Атанасян и др.
Автор: Софронова Наталия Андреевна,
учитель математики высшей категории
МОУ «Упшинская основная общеобразовательная школа»
Оршанского района Республики Марий Эл
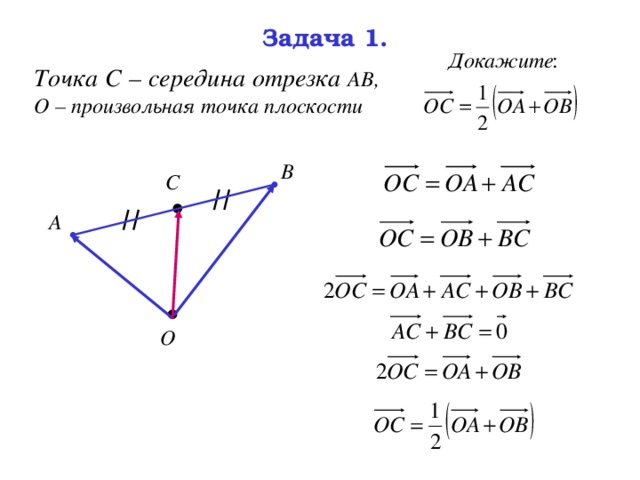
Точка С – середина отрезка АВ, О – произвольная точка плоскости
Доказать, что прямая, проведенная через середины оснований трапеции проходит через точку пересечения продолжений боковых сторон.
Задача 3 (продолжение).
лежат на одной прямой,
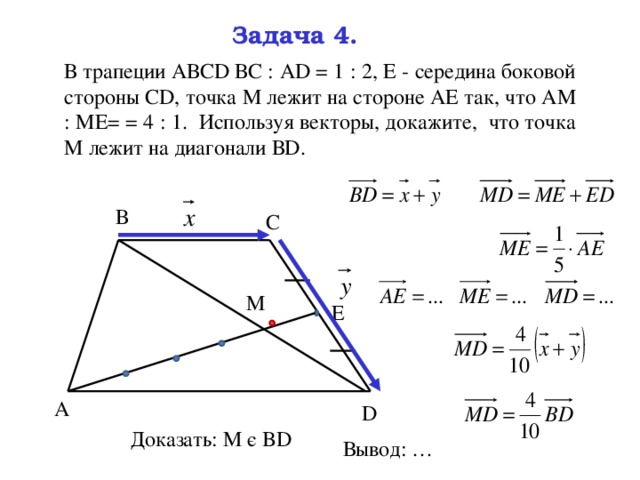
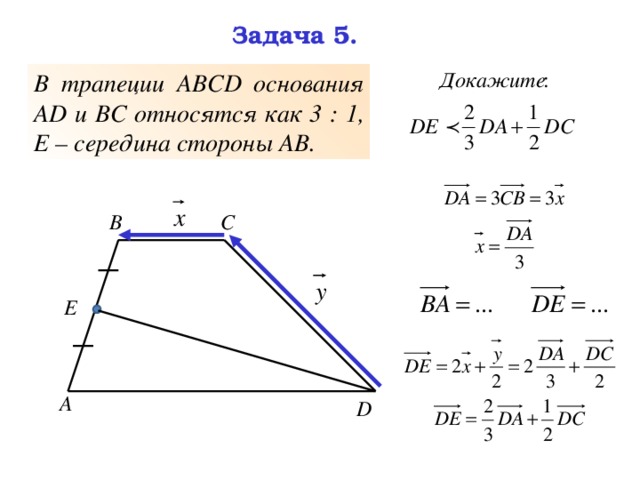
В трапеции АВСD основания АD и ВС относятся как 3 : 1, Е – середина стороны АВ.
Задача 5 (продолжение).
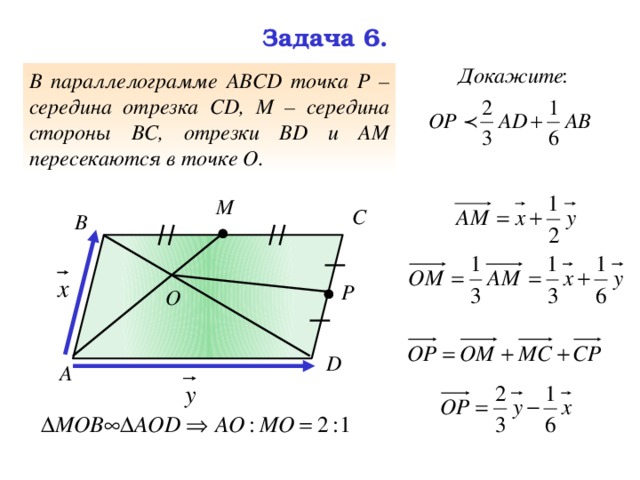
В параллелограмме АВСD точка Р – середина отрезка СD, М – середина стороны ВС, отрезки ВD и АМ пересекаются в точке О.
Задача 6 (продолжение).
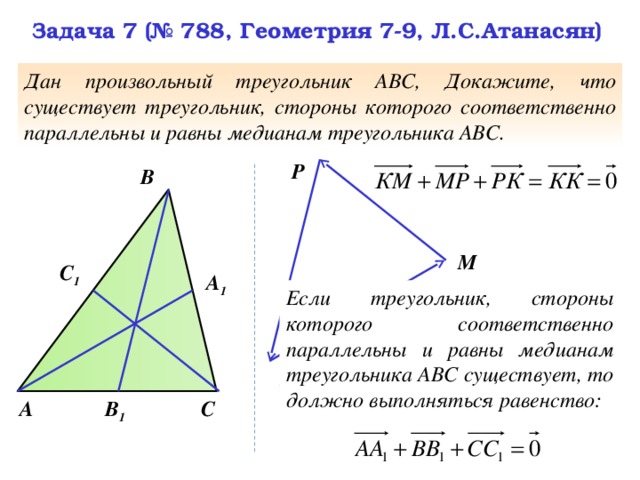
Задача 7 (№ 788, Геометрия 7-9, Л.С.Атанасян)
Дан произвольный треугольник АВС, Докажите, что существует треугольник, стороны которого соответственно параллельны и равны медианам треугольника АВС.
Если треугольник, стороны которого соответственно параллельны и равны медианам треугольника АВС существует, то должно выполняться равенство:
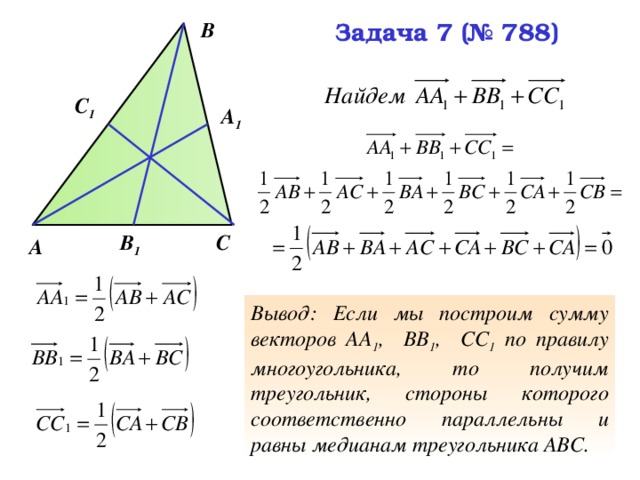
Вывод: Если мы построим сумму векторов АА 1 , ВВ 1 , СС 1 по правилу многоугольника, то получим треугольник, стороны которого соответственно параллельны и равны медианам треугольника АВС.
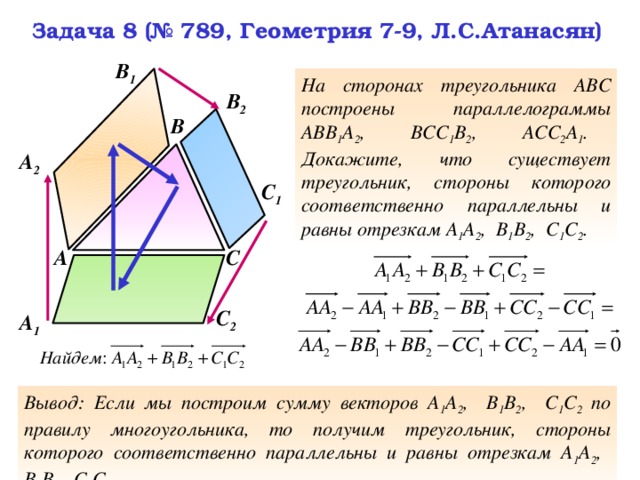
Задача 8 (№ 789, Геометрия 7-9, Л.С.Атанасян)
На сторонах треугольника АВС построены параллелограммы АВВ 1 А 2 , ВСС 1 В 2 , АСС 2 А 1 . Докажите, что существует треугольник, стороны которого соответственно параллельны и равны отрезкам А 1 А 2 , В 1 В 2 , С 1 С 2 .
Вывод: Если мы построим сумму векторов А 1 А 2 , В 1 В 2 , С 1 С 2 по правилу многоугольника, то получим треугольник, стороны которого соответственно параллельны и равны отрезкам А 1 А 2 , В 1 В 2 , С 1 С 2 .
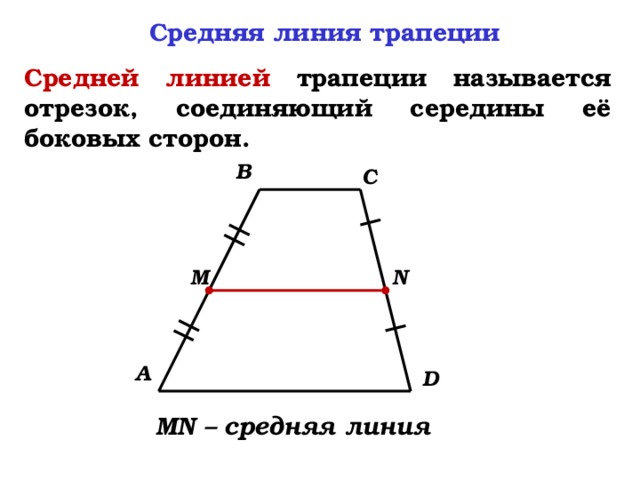
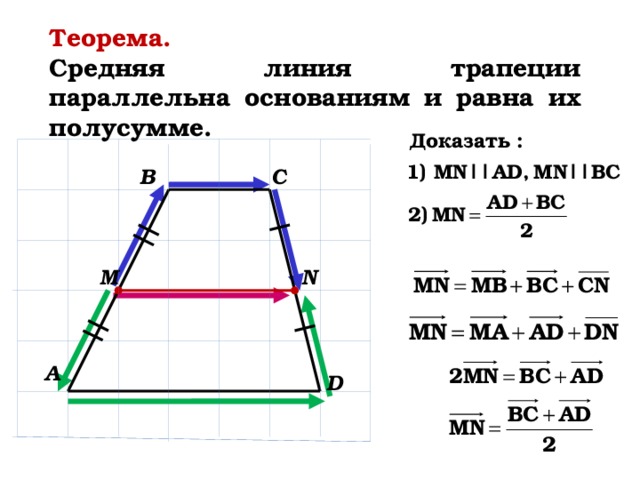
Средняя линия трапеции
Средней линией трапеции называется отрезок, соединяющий середины её боковых сторон.
Средняя линия трапеции параллельна основаниям и равна их полусумме.
Задачи по геометрии для самостоятельного решения 96817646 (Часть 5)
4.1. Алгебра векторов
4.3. Доказать, что точка B является серединой отрезка AC тогда и только тогда, когда для произвольной точки O выполняется оВ =
= 2 (oA + ос).
отрезке AC тогда и только тогда, когда Л £ [0; 1].
4.5. Доказать, что B £ [AC] тогда и только тогда, когда для любой точки O найдется такое число Л £ [0; 1], что оВ = (1 — Л)OA + лоС. Доказать, что при этом Л = |щ-.
4.12. Пусть —OA + oB + —C = Iе и \OA\ = \OB\ = \OC\. Доказать, что ABC — правильный треугольник.
4.13. _Пу сть M и N — середины отрезков AB и CD. Доказать, что
4.14. Доказать, что середины сторон произвольного выпуклого четырехугольника являются вершинами параллелограмма.
4.17. Доказать, что точка О является центром масс системы матери-
n равной массы тогда и только тогда, когда
OAi + OA2 + • • • + OAn — 0
4.18. Доказать, что центр масс системы материальных точек равной массы, расположенных в вершинах произвольного четырехугольника, совпадает с серединой отрезка, соединяющего середины диагоналей этого четырехугольника.
4.19. Пусть ABCD — произвольный тетраэдр. Доказать, что отрезки, соединяющие вершины с центрами масс противоположных граней, пересекаются в одной точке и делятся этой точкой в отношении 3:1, считая от вершины.
4.20. Пусть ABCD — произвольный тетраэдр. Доказать, что отрезки, соединяющие середины противоположных ребер пересекаются в одной точке и делятся этой точкой пополам.
4.21. Даны два треугольника ABC и AjB1C1 с центрами тяжести М и М1 соответственно. Доказать, что ММ1 = (AA1 + BB1 + CC1)/3.
4.22. Назовем средней линией произвольного четырехугольника отрезок, соединяющий середины несмежных сторон. Доказать, что: а) средние линии четырехугольника точкой пересечения делятся пополам; b) центр масс системы материальных точек равной массы, расположенных в вершинах четырехугольника, совпадает с серединой средней линии этого четырехугольника; с) две средние линии и две диагонали четырехугольника (всего четыре отрезка) пересекаются в одной точке тогда и только тогда, когда этот четырехугольник является параллелограммом; d) середины средних линий произвольного четырехугольника и середина отрезка, соединяющего середины диагоналей (всего три точки), совпадают.
4.23. Медиатрисой выпуклого четырехугольника называется отрезок, соединяющий одну из вершин этого четырехугольника с точкой пересеч-ния медиан треугольника, образованного остальными тремя вершинами четырехугольника. а) Доказать, что четыре медиатрисы выпуклого четырехугольника пересекаются в одной точке. b) В каком отношении точка пересечения медиатрис делит каждую из них?
4.24. Дан треугольник ABC. Точки A1 и B1 выбраны так, что A1 е [BC], B1 е [AC], причем \BA1\ : \A1C\ = \AB1\ : \B1C\ = 1:2. Точка O является пересечением отрезков [AA1] и [BB1]. а) Разложить вектор аО по базису С = aC, С = aB ; b) определить, в каком отношении точка O делит отрезки AA1 и BB1.
4.25. Дан треугольник ABC. На отрезках BC и AC соответственно выбраны точки A1 и B1 так, что \BA1\ : \A1C\ =3:1 и \AB1\ : \B1C\ = = 1:2. Точка O является пересечением отрезков [AA1] и [BB1 ]. а) Разложить вектор АС по базису с = aC, с = aB ; b) определить, в каком отношении точка O делит отрезки AA1 и BB1.
4.26. Даны четыре некомпланарных вектора
ct + b + C компланарны.
4.28. Для трех произвольных векторов —, i, — Доказать, что векторы — + —, — + —, — — it компланарны.
4.29. Известно, что векторы it,—,— не компланарны. Найти все значения p,q £ R, при которых векторы pit + q— + — и it + p— + q— коллинеарны.
4.30. Пусть ABCDEF — правильный шестиугольник, M — точка пространства, не лежащая в его плоскости. Принимая в качестве базис-
выражения для векторов a ) ME, MtC; b) CY, где Y — середина MF.
4.35. При каком x векторы M = (1,2, 5), it = (—1,3,13) и M = = (5,x, —29) компланарны?
4.44. Даны точки A(3, 2,1), B(-12,3, 5), C(6, 7,3). Найти координаты точки пересечения медиан треугольника ABC (т. е. его центра масс).
4.45. Найти расстояние от начала координат до центра окружности, описанной около треугольника с вершинами (1,0,1), (1,1,0) и (1,1,1) (систему координат считать декартовой).
4.48. Через концы трех ребер параллелепипеда, выходящих из одной вершины, проведена плоскость. Определить, в каком отношении она делит диагональ параллелепипеда, выходящую из той же вершины.
4.50. Доказать, что из медиан треугольника можно составить треугольник.
4.54. Даны два подобных четырехугольника OABC и OA1B1C1 с общей вершиной, лежащие в различных плоскостях. Доказать, что прямые (AA1), (BB1), (CC1) параллельны одной плоскости.
4.55. Прямая а пересекает стороны AB и AD параллелограмма
4.56. Доказать, что если O — центр вписанной в треугольник ABC окружности, а H — чточка пересечения высот этого треугольника, то
4.58. В параллелепипеде ABCDA1B1C1D1 через середину M ребра BC проведена прямая, пересекающая прямые ACi и DD1 соответственно в точках N и P. Найти отношение \MN\ : \NP|.
4.59. Дан параллелепипед ABCDAiB1C1D1, точка P — середина ребра AD. На прямых PB1 и BC1 взяты точки M, N так, что (MN)\\(A1C1). Найти \A1C1\ : \MN\.
4.67. Дана шестиугольная пирамида SABCDEF, в основании которой лежит правильный шестиугольник ABCDEF. Точки P, Q, R — середины ребер DE, EF, AS. Найти отношения, в которых секущая плоскость делит боковые ребра.
4.69. В призме ABCA1B1C1 медианы оснований ABC и A1B1C1 пересекаются соответственно в точках O и O1. Через середину отрезка OO1 проведена прямая, параллельная прямой CA1. Найти длину отрезка этой прямой, лежащего внутри призмы, если \CA1\ = a.
4.71. ABCDA1B1C1D1 — параллелепипед. Проведена прямая, пересекающая прямые AA1, BC и C1D1 соответственно в точках M, N и P так, что \MN\ : \MP\ = 2. Найти \CN\ : \BC\ (найти все решения).
4.73. Ребро куба ABCDA1B1C1D1 имеет длину a. На прямой BC1 взята точка M так, что прямые DA1, AB1 и D]_M параллельны одной плоскости. Найти длину отрезка D]_M.
4.74. Соответственно на ребре AD и диагонали A1C параллелепипеда ABCDA\B1C1D1 взяты точки M и N так, что прямая MN параллельна плоскости BDC1 и \AM\ : \AD\ = 1:5. Найти \CN\ : jCAij.
4.75. Пусть ABCDS — правильная четырехугольная пирамида. На ребрах AS и BS соответственно выбраны точки K и L так, что \AK\ : \KS\ = \SL\ : \LB\ = 1:3, а точка M — середина ребра SC. Точка N выбрана на прямой CD так, что прямые KL и NM пересекаются. Найти \DN\ : \NC\.
4.78. Даны две скрещивающиеся прямые m и n. На прямой m даны точки P, Q, R, а на прямой m — точки P1, Q1, R1, причем \PQ\ = = k\PR\, \P1Q1\ = k\P1R1\. Доказать, что прямые (PP1), (QQ1), (RR1) параллельны одной плоскости.
4.79 *. Даны два четырехугольника ABCD, A1B1C1D1, лежащие в различных плоскостях, O, O1 — точки пересечения их диагоналей. Доказать, что если \AO\ : \OC\ = \A1O1\ : \O1 C1\ и \BO\ : \OD\ = = \B1O1\ : \O1D1\, то прямые(AA1), (BB1), (CC1), (DD1) параллельны одной плоскости.
4.81 *. Даны два треугольника. Доказать, что если медианы одного из них параллельны сторонам другого, то и медианы второго из них параллельны сторонам первого.
4.84. Доказать, что биссектрисы двух плоских углов трехгранного угла и биссектриса угла, смежного с третьим плоским углом, лежат в одной плоскости.
4.85. Дан трехгранный угол. Доказать, что биссектрисы трех углов, смежных с его плоскими углами, лежат в одной плоскости.
4.86. Доказать, что три плоскости, каждая из которых проходит через биссектрису одного из плоских углов трехгранного угла и противолежащее этому плоскому углу ребро, пересекаются по некоторой прямой.
4.2. Скалярное произведение векторов. Разные задачи
ct равна 3, длина вектора b равна 4, а угол между этими векторами равен 2п/3. Вычислить (3
ct равна 2, длина вектора b равна 3. Известно, что (
a — b )2 = 56. Найти угол между векторами
4.91. Длины векторов
4.92. Какому условию должны удовлетворять векторы
4.93. Доказать, что вектор (
C) b перпендикулярен вектору
ct и н не перпендикулярны. Существует ли такое число к, что векторы
4.95. Даны три произвольных вектора
С. Доказать, что векторы ( b • н)
4.97. Используя векторы, доказать, что сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон.
4.98. Используя векторы, доказать, что сумма квадратов диагоналей параллелепипеда равна сумме квадратов всех его ребер.
4.100. Пусть O — начало координат. Записать уравнение плоскости, проходящей через точку N(3, 5, 2) и перпендикулярной вектору ON.
4.101. Плоскости а и в заданы уравнениями x + 2y — z + 1= 0 и 2x + 4y — 2z — 7 = 0 соответственно. Записать уравнение плоскости, параллельной обеим заданным плоскостям и находящейся от них на равных расстояниях.
4.102. Найти координаты точки, симметричной началу координат относительно плоскости, заданной уравнением 3x — 2y + z + 1 = 0.
4.105. Найти угол между плоскостями ABC и PQR, если A(—1,0,0), B(0, —1,0), C(0, 0, —1), P(2,1, 2), Q(0,1,4), R(4,0,0).
4.108. Ребро куба KLMNK1L1M1N1 имеет длину 1. Точки A и B лежат на ребрах KL и MM1 соответственно, причем \KA\ = 1, \BM1\ =
4.112. Найти расстояние от плоскости до сферы, если они соответственно заданы уравнениями 2x + 2y — z + 15 = 0 и x2 + y2 + z2 = 4.
4.113. Дан куб ABCDAiBiC\Di; точка M — середина ребра [CC1]. Найти косинус угла между векторами DAi и DM.
4.114. Дан куб ABCDA1B1C1D1. Используя векторы, найти угол между прямыми DA1 и AB1.
4.117. Используя векторы, найти угол и расстояние между скрещивающимися диагоналями смежных граней куба с ребром 1.
4.118. Дан куб ABCDA1B1C1D1 с ребром 1, точка M — центр грани CC1D1D. Найти расстояние от точки A до прямой BM.
4.119. Найти координаты точки, симметричной точке (0,1,0) относительно прямой, проходящей через точки (1, 0,0) и (1, 2,1).
4.123. ABCA1B1C1 — прямая треугольная призма, объем которой равен 3. Известно, что A(1, 0,1), B(2,0,0), C(0,1,0). Найти координаты точки Ai. Для тех, кто забыл: объем прямой призмы равен произведению площади ее основания на длину бокового ребра.
4.124. Плоскость, заданная уравнением x + y + z + D = 0, касается сферы, заданной уравнением x2 + y2 + z2 = 2x + 2y + 2z. Найти число D и координаты точки касания.
Группа Б
4.125. Используя векторы, доказать теорему Лейбница: если M — точка пересечения медиан треугольника ABC, то для любой точки X выполняется равенство
\XA\2 + \XB |2 + \XC |2 = 3|XM |2 + \MA\2 + \MB |2 + \MC\2.
4.126. Найти точку, сумма квадратов расстояний от которой до вершин данного треугольника минимальна.
— соответственно величины углов A, B и C данного треугольника).
4.135. В правильном тетраэдре DABC точка M — центр грани BCD, а точка K — середина ребра AC. Найти угол между прямыми AM и BK.
4.136. В правильном тетраэдре DABC точка O — центр грани ABC, а точки N, K и M — середины ребер AB, CD и AD соответственно. Найти угол между прямыми MO и KN.
4.137. Дана правильная треугольная призма ABCA1B1C1 с длиной ребра основания 1; O и O1 — центры треугольников ABC и A1B1C1 соответственно. Известно, что длина ортогональной проекции отрезка AO1 на прямую B1O равна |. Найти длину бокового ребра призмы.
4.138. Дана правильная треугольная призма ABCA1B1C1 с длиной ребра основания 1; O — центр треугольника ABC. а) Известно, что длина проекции отрезка A1O на прямую CB1 равна 1. Найти длину бокового ребра призмы. b) Найти расстояние от точки A1 до прямой OM, где M — центр грани BCC1B1.
4.141. В основании тетраэдра SABC лежит правильный треугольник ABC с длиной стороны 2у/2. Боковое ребро AS имеет длину 1 и перпендикулярно плоскости основания. Точки K и M — середины ребер
SB и CB соответственно. Найти: а) расстояние от точки A до плоскости SCB ; b) угол между плоскостями ABS и CBS; с) угол между прямыми AK и SM; d) расстояние между прямыми AK и SM.
4.142. Основанием пирамиды SABC является правильный треугольник ABC со стороной 4\/2. Ребро SC перпендикулярно плоскости ABC, \SC\ = 2, точки E и D — середины ребер BC и AB соответственно. Найти угол и расстояние между прямыми SE и CD.
4.143. Ребро куба ABCDA1B1C1D1 равно a. Квадрат A1B1C1D1 является основанием правильной пирамиды SA1B1C1D1 (точка S лежит вне куба), боковое ребро которой также равно a. Найти угол между прямыми AB и SCi.
4.147. Доказать, что из равенства длин отрезков, соединяющих середины противоположных ребер тетраэдра, вытекает перпендикулярность пар противоположных ребер.
4.148. Известно, что в тетраэдре суммы квадратов противоположных ребер попарно равны. Доказать, что противоположные ребра взаимно перпендикулярны.
4.152. В грани двугранного угла, равного 120°, проведена прямая, образующая угол 60° c ребром двугранного угла. Найти угол между этой прямой и другой гранью.
4.153. В основании прямой призмы ABCA1B1C1 лежит правильный треугольник ABC со стороной 1, прямые AC1 и BA1 перпендикулярны. Найти объем призмы.
4.154. а) Доказать, что сумма квадратов проекций всех ребер единичного куба на произвольную прямую не зависит от выбора этой прямой. b) Найти эту сумму.
4.155. В единичный куб вписана сфера. а) Доказать, что сумма квадратов расстояний от произвольной точки сферы до всех вершин куба не зависит от выбора этой точки. b) Найти эту сумму.
4.157. Дана пирамида DABC с основанием ABC, грани которой ABD и ACD — прямоугольные треугольники. Ребро AD перпендикулярно медиане AK основания пирамиды. Известно, что \AD\ = \AK\, точка E — середина отрезка BD, а точка G лежит на отрезке AC так, что \AG\ = 3|GC|. Кроме того, в пространстве взята точка H так, что EFGH — равнобедренная трапеция с основаниями EF и GH, причем плоскость EFGH не проходит через середины отрезков AD и BC. Найти отношение площадей трапеции EFGH и треугольника BCD.
4.159. В правильной треугольной пирамиде SABC (S — вершина, \SA\ = 4) точка D лежит на ребре SC, \CD\ = 3, а расстояние от точки A до прямой BD равно 2. Найти объем пирамиды.
4.161. В параллелограмме ABCD точка K — середина стороны BC, а точка M — середина стороны CD. Найти \AD\, если \AK\ = 6, \AM\ =3 и AKAM = 60°.
4.164. В правильной треугольной призме ABCAiBiCi длина стороны основания равна а, длина бокового ребра равна а/2. Точка D является ортогональной проекцией середины ребра AiCi на плоскость ABiC, а точка E — ортогональной проекцией точки D на плоскость AAiBiB. Найти объем пирамиды AiBiDE.
4.165. Сторона основания ABCD правильной пирамиды SABCD имеет длину а, боковое ребро — длину 2а. Рассматриваются отрезки с концами на диагонали BD основания и боковом ребре SC, параллельные плоскости (SAD). а) Один из этих отрезков проведен через точку M диагонали BD так, что \DM| : \DB| = 1:3. Найти его длину. b) Найти наименьшую длину всех рассматриваемых отрезков.
4.166. В основании треугольной пирамиды SABC лежит правильный треугольник ABC со стороной 1, ребро SA пирамиды перпендикулярно плоскости основания, \SA\ = л/3. Плоскость а параллельна прямым SB и AC, плоскость впараллельна прямым SC и AB. Определить величину угла между плоскостями а и в.
Используя векторы докажите что середина отрезка bb1 лежит на прямой aa1
Дана прямая треугольная призма ABCA1B1C1. Известно, что AB = BC. Точка K — середина ребра A1B1, а точка M лежит на ребре AC и делит его в отношении AM : MC = 1 : 3.
б) Найдите расстояние между прямыми KM и A1C1, если AB = 10, AC = 8 и AA1 = 3.
а) Пусть точка L лежит на ребре A1C1 и делит его в отношении A1L : LC1 = 1 : 3. Поскольку треугольник ABC равнобедренный, треугольник A1B1C1 тоже равнобедренный. Следовательно, отрезок KL перпендикулярен стороне A1C1. Отрезок ML тоже перпендикулярен стороне A1C1. Получаем, что прямая A1C1 перпендикулярна плоскости KLM, то есть прямая KM перпендикулярна прямой A1C1, а, следовательно, и прямой AC.
б) Пусть LH — высота треугольника KLM. Так как прямая A1C1 перпендикулярна плоскости KLM, расстояние между прямыми KM и A1C1, равно LH. Тогда LM = AA1 = 3,
Значит, KL · LM = KM · LH,
Ответ:
| Критерии оценивания выполнения задания | Баллы | ||||||
|---|---|---|---|---|---|---|---|
| Имеется верное доказательство утверждения пункта a) и обоснованно получен верный ответ в пункте б) | 3 | ||||||
| Получен обоснованный ответ в пункте б) имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | 2 | ||||||
| Имеется верное доказательство утверждения пункта а) при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, Используя векторы докажите что середина отрезка bb1 лежит на прямой aa1На ребре AA1 прямоугольного параллелепипеда ABCDA1B1C1D1 взята точка E так, что A1E : EA = 5 : 3, на ребре BB1 — точка F так, что B1F : FB = 5 : 11, а точка T − середина ребра B1C1. Известно, что а) Докажите, что плоскость EFT проходит через вершину D1. б) Найдите площадь сечения параллелепипеда плоскостью EFT. Значит, треугольники D1A1E и TB1F подобны, причём прямые D1A1 и B1C1 параллельны, прямые A1E и B1F тоже параллельны. Поэтому прямые ED1 и FT также параллельны. Если плоскость EFT не проходит через точку D1, то получается, что в плоскости AA1D1D через точку E проходят две различные прямые, параллельные прямой FT. Получили противоречие. б) Сечение параллелепипеда плоскостью EFT — трапеция. Проведём через точку F прямую, параллельную прямой AB. Получим точку P на ребре AA1. Следовательно, EF = D1T, и трапеция EFTD1 равнобедренная. Проведём в ней высоту TH. Тогда
|