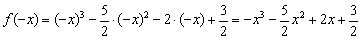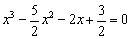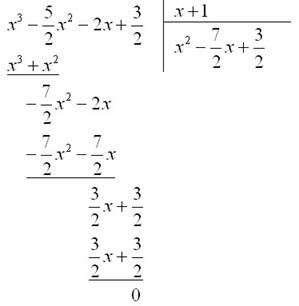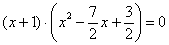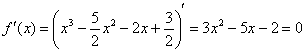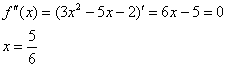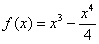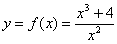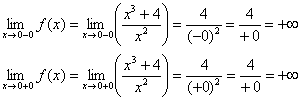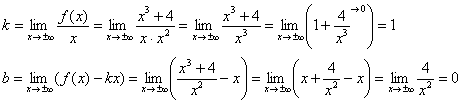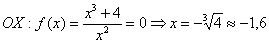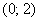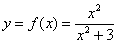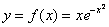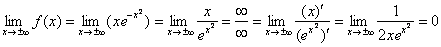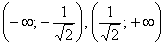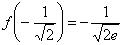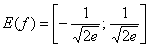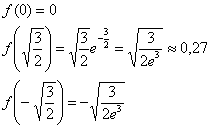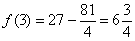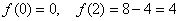Исследование функции для чего нужно

Полное исследование функции и построение графика.

Стоит задача: провести полное исследование функции и построить ее график .

Каждый студент прошел через подобные задачи.

Дальнейшее изложение предполагает хорошее знание свойств и графиков основных элементарных функций. Рекомендуем обращаться к этому разделу при возникновении вопросов.

Алгоритм исследования функции состоит из следующих шагов.

Нахождение области определения функции.

Это очень важный шаг исследования функции, так как все дальнейшие действия будут проводиться на области определения.

В нашем примере нужно найти нули знаменателя и исключить их из области действительных чисел.

(В других примерах могут быть корни, логарифмы и т.п. Напомним, что в этих случаях область определения ищется следующим образом:
для корня четной степени, например, — область определения находится из неравенства ;
для логарифма — область определения находится из неравенства ).

Исследование поведения функции на границе области определения, нахождение вертикальных асимптот.

На границах области определения функция имеет вертикальные асимптоты, если односторонние пределы функции в этих граничных точках бесконечны.

В нашем примере граничными точками области определения являются .

Исследуем поведение функции при приближении к этим точкам слева и справа, для чего найдем односторонние пределы:

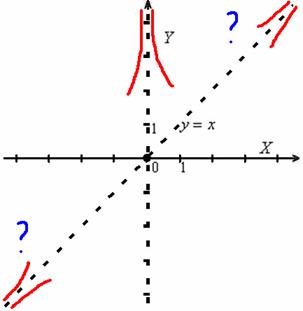
Так как односторонние пределы бесконечны, то прямые являются вертикальными асимптотами графика.

Исследование функции на четность или нечетность.

Функция является четной, если . Четность функции указывает на симметрию графика относительно оси ординат.

Функция является нечетной, если . Нечетность функции указывает на симметрию графика относительно начала координат.

Если же ни одно из равенств не выполняется, то перед нами функция общего вида.

Нахождение промежутков возрастания и убывания функции, точек экстремума.

Промежутки возрастания и убывания являются решениями неравенств и соответственно.

Точки, в которых производная обращается в ноль, называют стационарными.

Критическими точками функции называют внутренние точки области определения, в которых производная функции равна нулю или не существует.

Мы будем включать критические точки в промежутки возрастания и убывания, если они принадлежат области определения функции.

Находим производную на области определения (при возникновении сложностей, смотрите раздел дифференцирование функции, нахождение производной).

Наносим эти точки на числовую ось и определяем знак производной внутри каждого полученного промежутка. Как вариант, можно взять любую точку из промежутка и вычислить значение производной в этой точке. Если значение положительное, то ставим плюсик над этим промежутком и переходим к следующему, если отрицательное, то ставим минус и т.д. К примеру, , следовательно, над первым слева интервалом ставим плюс.

Схематично плюсами / минусами отмечены промежутки где производная положительна / отрицательна. Возрастающие / убывающие стрелочки показывают направление возрастания / убывания.

Точками экстремума функции являются точки, в которых функция определена и проходя через которые производная меняет знак.

Нахождение промежутков выпуклости и вогнутости функции и точек перегиба.

Промежутки вогнутости и выпуклости функции находятся при решениями неравенств и соответственно.

Иногда вогнутость называют выпуклостью вниз, а выпуклость – выпуклостью вверх.

Здесь также справедливы замечания, подобные замечаниям из пункта про промежутки возрастания и убывания.

Находим вторую производную на области определения.

Далее ищем нули числителя и знаменателя.

В нашем примере нулей числителя нет, нули знаменателя .

Наносим эти точки на числовую ось и определяем знак второй производной внутри каждого полученного промежутка.

Другими словами, точками перегиба могут являться точки, проходя через которые вторая производная меняет знак, в самих точках либо равна нулю, либо не существует, но эти точки входят в область определения функции.

В нашем примере точек перегиба нет, так как вторая производная меняет знак проходя через точки , а они не входят в область определения функции.

Нахождение горизонтальных и наклонных асимптот.

Горизонтальные или наклонные асимптоты следует искать лишь тогда, когда функция определена на бесконечности.

Наклонные асимптоты ищутся в виде прямых , где и .

Если k=0 и b не равно бесконечности, то наклонная асимптота станет горизонтальной.

Кто такие вообще эти асимптоты?

Это такие линии, к которым приближается график функции на бесконечности. Таким образом, они очень помогают при построении графика функции.

Если горизонтальных или наклонных асимптот нет, но функция определена на плюс бесконечности и (или) минус бесконечности, то следует вычислить предел функции на плюс бесконечности и (или) минус бесконечности, чтобы иметь представление о поведении графика функции.

Для нашего примера

— горизонтальная асимптота.

На этом с исследование функции завершается, переходим к построению графика.

Вычисляем значения функции в промежуточных точках.

Для более точного построения графика рекомендуем найти несколько значений функции в промежуточных точках (то есть в любых точках из области определения функции).

Сначала строим асимптоты, наносим точки локальных максимумов и минимумов функции, точки перегиба и промежуточные точки. Для удобства построения графика можно нанести и схематическое обозначение промежутков возрастания, убывания, выпуклости и вогнутости, не зря же мы проводили исследование функции =).

Осталось провести линии графика через отмеченные точки, приближая к асимптотам и следуя стрелочкам.

Этим шедевром изобразительного искусства задача полного исследования функции и построения графика закончена.

Графики некоторых элементарных функций можно строить с использованием геометрических преобразований графиков основных элементарных функций.

Источник

Общая схема исследования и построения графика функции

п.1. Алгоритм исследования и построения графика функции

1. Найти область определения функции, классифицировать точки разрыва
2. Исследовать функцию на четность и периодичность
3. Провести анализ асимптотического поведения функции (наличие вертикальных, горизонтальных и наклонных асимптот) (см. §41 данного справочника)
4. Взять первую производную. Определить критические точки, интервалы монотонности, точки экстремума
5. Взять вторую производную. Определить критические точки 2-го порядка, интервалы выпуклости и точки перегиба
6. Найти точки пересечения функции с осями координат (если уравнение \(f(x)=0\) не имеет аналитического решения, указать количество точек пересечения с осью OX)
7. Построить график функции

п.2. Примеры

Пример 1. Постройте график функции \(y=2x^3-6x^2-18x+7\)
1) Область определения \(x\in\mathbb\)
Точек разрыва нет

4) Первая производная \begin f'(x)=2\cdot 3x^2-6\cdot 2x-18\cdot 1+0=6x^2-12x-18=6(x^2-2x-3)=\\ =6(x-3)(x+1)\\ f'(x)=0\ \text<при>\ \left[ \begin x=3\\ x=-1 \end \right. \end Критические точки: \(x=-1\) и \(x=3\)
Составляем таблицу:

Функция возрастает при \(x\in(-\infty;-1)\cup(3;+\infty)\)
Функция убывает при \(x\in(-1;3)\)
Точка максимума \(x=-1;\ y_=f(-1)=-2-6+18+7=17\)
Точка минимума \(x=3;\ y_=f(3)=54-54-54+7=-47\)

5) Вторая производная: \begin f»(x)=(6x^2-12x-18)’=6\cdot 2x-12\cdot 1-0=12x-12=12(x-1)\\ f»(x)=0\ \text<при>\ x=1 \end Критическая точка 2-го порядка: \(x=1\)
Составляем таблицу:

Функция выпуклая вверх при \(x\in(-\infty;1)\)
Функция выпуклая вниз при \(x\in(1;+\infty)\)
Точка перегиба \(x=1;\ f(1)=2-6-18+7=-15\)

Функция возрастает при \(x\in(-\infty;-3)\cup(-3;+\infty)\)
Функция убывает при \(x\in(-3;0)\cup(0;3)\)
Точка максимума \(x=-3;\ y_=f(-3)=-1-1=-2\)
Точка минимума \(x=3;\ y_=f(3)=1+1=2\)

5) Вторая производная: \begin f»(x)=\frac13\left(1-\frac<9>\right)’=\frac13\left(0+\frac<9\cdot 2>\right)=\frac<6> \end Вторая производная нулей не имеет.
Критическая точка 2-го порядка: \(x=0\)
Составляем таблицу:

Функция выпуклая вверх при \(x\in(-\infty;0)\)
Функция выпуклая вниз при \(x\in(0;+\infty)\)
Точек перегиба нет.

7) График

Пример 3*. Постройте график функции \(y=\frac<(x-1)^3>\)
Сколько корней имеет уравнение \(\frac<(x-1)^3>=a\)?

7) График

Ответ:
\(a\lt\frac49\cup a\gt 4\), один корень
\(a=\left\<\frac49;1;4\right\>\), два корня
\(\frac<12><27>\lt 1\lt 1\cup 1\lt a\lt 4\), три корня

Пример 4*. Постройте график функции \(y=sin^4⁡x+cos^4⁡x\), используя правила преобразования тригонометрических функций и с помощью стандартной процедуры исследования функции

1) Область определения \(x\in\mathbb\)

Получаем график:

Продолжим стандартное исследование функции.

3) Асимптоты
1. Вертикальных асимптот нет, т.к. нет точек разрыва 2-го рода.
2. Горизонтальных асимптот нет, т.к. нет пределов на бесконечности.
3. Наклонных асимптот нет, т.к. на бесконечности отношение ограниченной тригонометрической функции к бесконечному x дает \(k=0\).

4) Первая производная:
Исследуем промежуток, равный одному периоду \(T=\frac\pi 2,\ 0\leq x\leq\frac\pi 2\) \begin f'(x)=(sin^4 x+cos^4 x)’=\left(\frac<3+cos4x><4>\right)’=0-\frac14\cdot 4\cdot sin4x=-sin4x\\ sin4x=0\Rightarrow 4x=\pi k\Rightarrow x=\frac<\pi k> <4>\end Критические точки: \(x=\frac<\pi k><4>\). На периоде \(T=\frac\pi 2\) получаем три точки \(x=\left\<0;\frac\pi 4;\frac\pi 2\right\>\)

Функция убывает при \(x\in\left(\frac<\pi k><2>;\frac\pi 4+\frac<\pi k><2>\right)\)
Функция возрастает при \(x\in\left(\frac\pi 4+\frac<\pi k><2>;\frac\pi 2+\frac<\pi k><2>\right)\)
Точки минимума \(x=\frac\pi 4+\frac<\pi k><2>;\ y_=\frac12\)
Точки максимума \(x=\frac<\pi k><2>;\ y_=1\)

5) Вторая производная: \begin f»(x)=(-sin4x)’=-4cos4x\\ cos4x=0\Rightarrow 4x=\frac\pi 2+\pi k\Rightarrow x=\frac\pi 8+\frac<\pi k> <4>\end Критические точки 2-го порядка: \(x=\frac\pi 8+\frac<\pi k><4>\).
На периоде \(T=\frac\pi 2\) получаем две точки \(x=\left\<\frac\pi 8;\frac<3\pi><8>\right\>\)

Источник

Полное исследование функции и построение графика

Для решения задачи данного типа следует использовать свойства и графики основных элементарных функций. Алгоритм исследования включает в себя шаги:

Нахождение области определения

Так как исследования проводятся на области определения функции, необходимо начинать с этого шага.

Заданный пример предполагает нахождение нулей знаменателя для того, чтобы исключить их из ОДЗ.

Исследование границ ОДЗ и нахождение вертикальных асимптот

На границах функции имеются вертикальные асимптоты, когда односторонние пределы в таких точках бесконечны.

Исследование функции и на четность или нечетность

Нахождение возрастания и убывания, точек экстремума

Для решения неравенства применяются промежутки возрастания и убывания с условиями f ‘ ( x ) ≥ 0 и f ‘ ( x ) ≤ 0 соответственно.

Стационарные точки – это такие точки, которые обращают производную в ноль.

При решении необходимо учитывать следующие замечания:

Включение критических точек в промежутки возрастания и убывания в том случае, если они удовлетворяют области определения функции.

Для определения промежутков возрастания и убывания функции необходимо найти:

Решение

Ответ:

Точки экстремума функции – точки, где функция определена и через которые производная меняет знак.

Нахождение промежутков выпуклости и вогнутости функции и точек перегиба

Для определения промежутков вогнутости и выпуклости необходимо:

Найти вторую производную из области определения.

Решение

Находим нули числителя и знаменателя, где на примере нашего примера имеем, что нули знаменателя x = ± 1 2

Теперь необходимо нанести точки на числовую ось и определить знак второй производной из каждого промежутка. Получим, что

Ответ:

Иначе говоря, это такая точка, через которую проходит вторая производная и меняет знак, а в самих точках равняется нулю или не существует. Все точки считаются областью определения функции.

Нахождение горизонтальных и наклонных асимптот

При определении функции на бесконечности нужно искать горизонтальные и наклонные асимптоты.

Иначе говоря, асимптотами считают линии, к которым приближается график функции на бесконечности. Это способствует быстрому построению графика функции.

Если асимптоты отсутствуют, но функция определяется на обеих бесконечностях, необходимо посчитать предел функции на этих бесконечностях, чтобы понять, как себя будет вести график функции.

На примере рассмотрим, что

является горизонтальной асимптотой. После исследования функции можно приступать к ее построению.

Вычисление значения функции в промежуточных точках

Чтобы построение графика было наиболее точным, рекомендовано находить несколько значений функции в промежуточных точках.

Построение графика

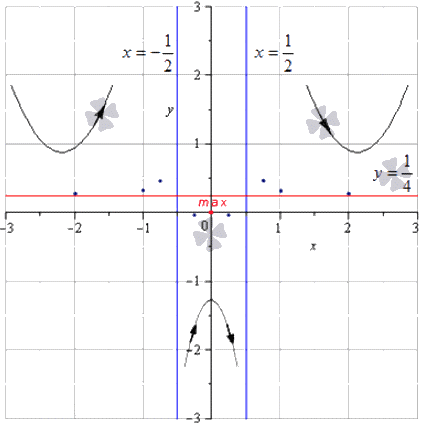
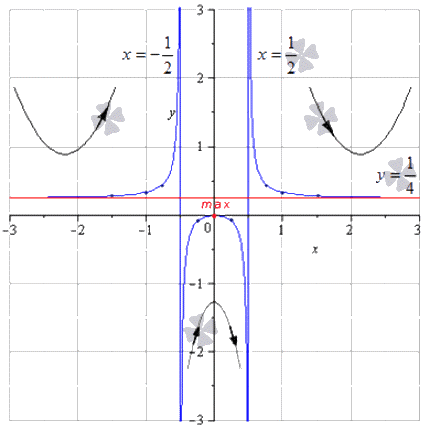
Для определения максимумов и минимумов функции, точек перегиба, промежуточных точек необходимо строить асимптоты. Для удобного обозначения фиксируются промежутки возрастания, убывания, выпуклость, вогнутость. Рассмотрим на рисунке, изображенном ниже.

Необходимо через отмеченные точки проводить линии графика, что позволит приблизить к асимптотам, следуя стрелочкам.

На этом заканчивается полное исследование функции. Встречаются случаи построения некоторых элементарных функций, для которых применяют геометрические преобразования.

Источник

Как исследовать функцию и построить её график?

Похоже, я начинаю понимать одухотворённо-проникновенный лик вождя мирового пролетариата, автора собрания сочинений в 55 томах…. Нескорый путь начался элементарными сведениями о функциях и графиках, и вот сейчас работа над трудоемкой темой заканчивается закономерным результатом – статьёй о полном исследовании функции. Долгожданное задание формулируется следующим образом:

Исследовать функцию методами дифференциального исчисления и на основании результатов исследования построить её график

Или короче: исследовать функцию и построить график.

Зачем исследовать? В простых случаях нас не затруднит разобраться с элементарными функциями, начертить график, полученный с помощью элементарных геометрических преобразований и т.п. Однако свойства и графические изображения более сложных функций далеко не очевидны, именно поэтому и необходимо целое исследование.

Основные этапы решения сведены в справочном материале Схема исследования функции, это ваш путеводитель по разделу. Чайникам требуется пошаговое объяснение темы, некоторые читатели не знают с чего начать и как организовать исследование, а продвинутым студентам, возможно, будут интересны лишь некоторые моменты. Но кем бы вы ни были, уважаемый посетитель, предложенный конспект с указателями на различные уроки в кратчайший срок сориентирует и направит Вас в интересующем направлении. Роботы прослезились =) Руководство свёрстано в виде pdf-файла и заняло заслуженное место на странице Математические формулы и таблицы.

Исследование функции я привык разбивать на 5-6 пунктов:

1) Область определения, непрерывность, четность/нечётность, периодичность функции.

2) Асимптоты графика функции.

6) Дополнительные точки и график по результатам исследования.

На счёт заключительного действия, думаю, всем всё понятно – будет очень обидно, если в считанные секунды его перечеркнут и вернут задание на доработку. ПРАВИЛЬНЫЙ И АККУРАТНЫЙ ЧЕРТЁЖ – это основной результат решения! Он с большой вероятностью «прикроет» аналитические оплошности, в то время как некорректный и/или небрежный график доставит проблемы даже при идеально проведённом исследовании.

Следует отметить, что в других источниках количество пунктов исследования, порядок их выполнения и стиль оформления могут существенно отличаться от предложенной мной схемы, но в большинстве случаев её вполне достаточно. Простейшая версия задачи состоит всего из 2-3 этапов и формулируется примерно так: «исследовать функцию с помощью производной и построить график» либо «исследовать функцию с помощью 1-й и 2-й производной, построить график».

Естественно – если в вашей методичке подробно разобран другой алгоритм или ваш преподаватель строго требует придерживаться его лекций, то придётся внести некоторые коррективы в решение. Не сложнее, чем заменить вилку бензопилой ложкой.

Итак, вооружившись общей схемой исследования, где рассмотрена структура и техника выполнения задачи, переходим к изучению стратегии и тактики действий. Успешно прошедшим курс обучения откроется тайна числа 69 😉 С нетерпением скрипим колёсиком мыши =)

Исследовать функцию и по результатам исследования построить график.

Решение:
1) Функция определена и непрерывна на всей числовой прямой: 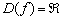. Это очень хорошо, отпадают вертикальные асимптоты.

Проверим функцию на чётность/нечётность:

После чего следует шаблонная отписка: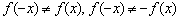
, значит, данная функция не является чётной или нечётной.

Очевидно, что функция непериодическая.

2) Асимптоты, поведение функции на бесконечности.

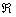
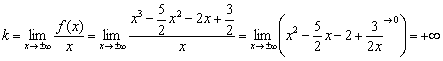
Так как функция непрерывна на , то вертикальные асимптоты отсутствуют.

Нет и наклонных асимптот.

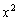
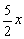
Примечание: напоминаю, что более высокого порядка роста, чем , поэтому итоговый предел равен именно «плюс бесконечности».

Выясним, как ведёт себя функция на бесконечности:

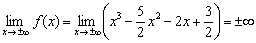
Иными словами, если идём вправо, то график уходит бесконечно далеко вверх, если влево – бесконечно далеко вниз. Да, здесь тоже два предела под единой записью. Если у вас возникли трудности с расшифровкой знаков 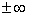, пожалуйста, посетите урок о бесконечно малых функциях.

Таким образом, функция не ограничена сверху и не ограничена снизу. Учитывая, что у нас нет точек разрыва, становится понятна и область значений функции: 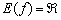– тоже любое действительное число.

ПОЛЕЗНЫЙ ТЕХНИЧЕСКИЙ ПРИЁМ

Каждый этап задания приносит новую информацию о графике функции, поэтому в ходе решения удобно использовать своеобразный МАКЕТ. Изобразим на черновике декартову систему координат. Что уже точно известно? Во-первых, у графика нет асимптот, следовательно, прямые чертить не нужно. Во-вторых, мы знаем, как функция ведёт себя на бесконечности. Согласно проведённому анализу, нарисуем первое приближение: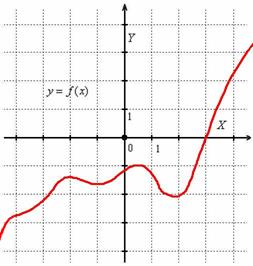

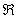
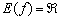
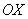
Заметьте, что в силу непрерывности функции на и того факта, что , график должен, по меньшей мере, один раз пересечь ось . А может быть точек пересечения несколько?

3) Нули функции и интервалы знакопостоянства.

Сначала найдём точку пересечения графика с осью ординат. Это просто. Необходимо вычислить значение функции при :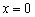

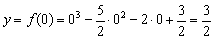
Полтора над уровнем моря.

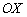
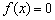
Чтобы найти точки пересечения с осью (нули функции) требуется решить уравнение , и тут нас поджидает неприятный сюрприз:

В конце притаился свободный член, который существенно затрудняет задачу.

Такое уравнение имеет, как минимум, один действительный корень, и чаще всего этот корень иррационален. В худшей же сказке нас поджидают три поросёнка. Уравнение разрешимо с помощью так называемых формул Кардано, но порча бумаги сопоставима чуть ли не со всем исследованием. В этой связи разумнее устно либо на черновике попытаться подобрать хотя бы один целый корень. Проверим, не являются ли оными числа :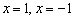
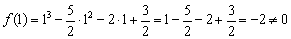
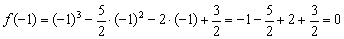
– не подходит;
– есть!

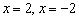
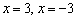
Здесь повезло. В случае неудачи можно протестировать ещё и , а если и эти числа не подошли, то шансов на выгодное решение уравнения, боюсь, очень мало. Тогда пункт исследования лучше полностью пропустить – авось станет что-нибудь понятнее на завершающем шаге, когда будут пробиваться дополнительные точки. И если таки корень (корни) явно «нехорошие», то об интервалах знакопостоянства лучше вообще скромно умолчать да поаккуратнее выполнить чертёж.

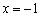
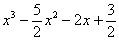
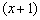
Однако у нас есть красивый корень , поэтому делим многочлен на без остатка:

Алгоритм деления многочлена на многочлен детально разобран в первом примере урока Сложные пределы.

В итоге левая часть исходного уравнения 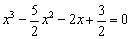раскладывается в произведение:

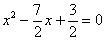
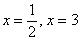
А теперь немного о здоровом образе жизни. Я, конечно же, понимаю, что квадратные уравнения нужно решать каждый день, но сегодня сделаем исключение: уравнение имеет два действительных корня .

На числовой прямой отложим найденные значения 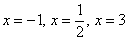и методом интервалов определим знаки функции:

Таким образом, на интервалах 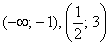график расположен
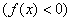
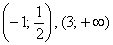
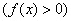
ниже оси абсцисс , а на интервалах – выше данной оси .

Полученные выводы позволяют детализировать наш макет, и второе приближение графика выглядит следующим образом: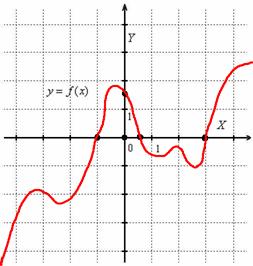

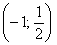
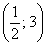
Обратите внимание, что на интервале функция обязательно должна иметь хотя бы один максимум, а на интервале – хотя бы один минимум. Но сколько раз, где и когда будет «петлять» график, мы пока не знаем. К слову, функция может иметь и бесконечно много экстремумов.

4) Возрастание, убывание и экстремумы функции.

Найдём критические точки:

Данное уравнение имеет два действительных корня 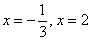. Отложим их на числовой прямой и определим знаки производной:

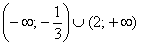
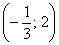
Следовательно, функция возрастает на и убывает на .
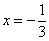
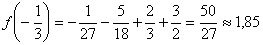
В точке функция достигает максимума: .
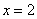
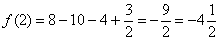
В точке функция достигает минимума: .

Установленные факты загоняют наш шаблон в довольно жёсткие рамки: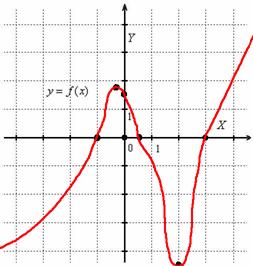

Что и говорить, дифференциальное исчисление – штука мощная. Давайте окончательно разберёмся с формой графика:

5) Выпуклость, вогнутость и точки перегиба.

Найдём критические точки второй производной:

Определим знаки :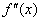

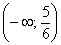
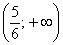
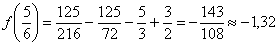
График функции является выпуклым на и вогнутым на . Вычислим ординату точки перегиба: .

Практически всё прояснилось.

6) Осталось найти дополнительные точки, которые помогут точнее построить график и выполнить самопроверку. В данном случае их мало, но пренебрегать не будем:

Выполним чертёж: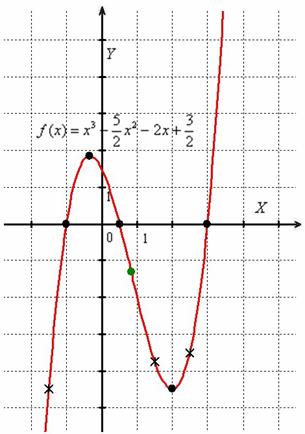

Зелёным цветом отмечена точка перегиба, крестиками – дополнительные точки. График кубической функции симметричен относительно своей точки перегиба, которая всегда расположена строго посередине между максимумом и минимумом.

По ходу выполнения задания я привёл три гипотетических промежуточных чертежа. На практике же достаточно нарисовать систему координат, отмечать найденные точки и после каждого пункта исследования мысленно прикидывать, как может выглядеть график функции. Студентам с хорошим уровнем подготовки не составит труда провести такой анализ исключительно в уме без привлечения черновика.

Для самостоятельного решения:

Исследовать функцию и построить график.

Тут всё быстрее и веселее, примерный образец чистового оформления в конце урока.

Немало секретов раскрывает исследование дробно-рациональных функций:

Методами дифференциального исчисления исследовать функцию и на основании результатов исследования построить её график.

Решение: первый этап исследования не отличается чем-то примечательным, за исключением дырки в области определения:

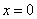
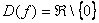
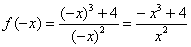
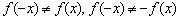
1) Функция определена и непрерывна на всей числовой прямой кроме точки , область определения: .

, значит, данная функция не является четной или нечетной.

Очевидно, что функция непериодическая.

График функции представляет собой две непрерывные ветви, расположенные в левой и правой полуплоскости – это, пожалуй, самый важный вывод 1-го пункта.

2) Асимптоты, поведение функции на бесконечности.

а) С помощью односторонних пределов исследуем поведение функции вблизи подозрительной точки, где явно должна быть вертикальная асимптота:

Действительно, функции терпит бесконечный разрыв в точке ,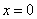
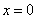
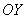
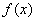
а прямая (ось ) является вертикальной асимптотой графика .

б) Проверим, существуют ли наклонные асимптоты:

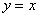
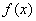
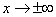
Да, прямая является наклонной асимптотой графика , если .

Пределы 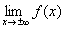анализировать смысла не имеет, поскольку и так понятно, что функция в обнимку со своей наклонной асимптотой не ограничена сверху и не ограничена снизу.

Второй пункт исследования принёс много важной информации о функции. Выполним черновой набросок:

Вывод № 1 касается интервалов знакопостоянства. На «минус бесконечности» график функции однозначно расположен ниже оси абсцисс, а на «плюс бесконечности» – выше данной оси. Кроме того, односторонние пределы сообщили нам, что и слева и справа от точки 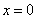функция тоже больше нуля. Обратите внимание, что в левой полуплоскости график, по меньшей мере, один раз обязан пересечь ось абсцисс. В правой полуплоскости нулей функции может и не быть.

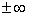
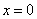
Вывод № 2 состоит в том, что функция возрастает на и слева от точки (идёт «снизу вверх»). Справа же от данной точки – функция убывает (идёт «сверху вниз»). У правой ветви графика непременно должен быть хотя бы один минимум. Слева экстремумы не гарантированы.

Вывод № 3 даёт достоверную информацию о вогнутости графика в окрестности точки 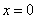. О выпуклости/вогнутости на бесконечностях мы пока ничего сказать не можем, поскольку линия может прижиматься к своей асимптоте как сверху, так и снизу. Вообще говоря, есть аналитический способ выяснить это прямо сейчас, но форма графика «даром» прояснится на более поздних этапах.

Зачем столько слов? Чтобы контролировать последующие пункты исследования и не допустить ошибок! Дальнейшие выкладки не должны противоречить сделанным выводам.

3) Точки пересечения графика с координатными осями, интервалы знакопостоянства функции.

График функции не пересекает ось .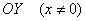

С осью

Методом интервалов определим знаки :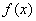

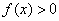
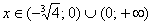
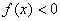
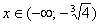
, если ;
, если .

Результаты пункта полностью соответствуют Выводу № 1. После каждого этапа смотрите на черновик, мысленно сверяйтесь с исследованием и дорисовывайте график функции.

4) Возрастание, убывание, экстремумы функции.

В рассматриваемом примере числитель почленно делится на знаменатель, что очень выгодно для дифференцирования: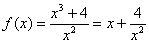

Собственно, это уже проделывалось при нахождении асимптот.

– критическая точка.

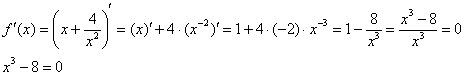
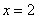
Определим знаки :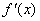

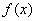
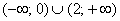
возрастает на и убывает на

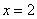
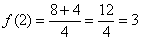
В точке функция достигает минимума: .

Разночтений с Выводом № 2 также не обнаружилось, и, вероятнее всего, мы на правильном пути.

5) Выпуклость, вогнутость, перегибы графика.

, значит, график функции является вогнутым на всей области определения.

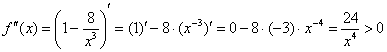
Отлично – и чертить ничего не надо.

Точки перегиба отсутствуют.

Вогнутость согласуется с Выводом № 3, более того, указывает, что на бесконечности (и там и там) график функции расположен выше своей наклонной асимптоты.

6) Добросовестно приколотим задание дополнительными точками. Вот здесь придётся изрядно потрудиться, поскольку из исследования нам известны только две точки.

И картинка, которую, наверное, многие давно представили:

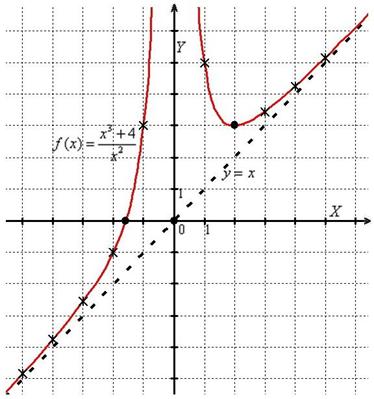
В ходе выполнения задания нужно тщательно следить за тем, чтобы не возникало противоречий между этапами исследования, но иногда ситуация бывает экстренной или даже отчаянно-тупиковой. Вот «не сходится» аналитика – и всё тут. В этом случае рекомендую аварийный приём: находим как можно больше точек, принадлежащих графику (сколько хватит терпения), и отмечаем их на координатной плоскости. Графический анализ найденных значений в большинстве случаев подскажет, где правда, а где ложь. Кроме того, график можно предварительно построить с помощью какой-нибудь программы, например, в том же Экселе (понятно, для этого нужны навыки).

Методами дифференциального исчисления исследовать функцию и построить её график.

Это пример для самостоятельного решения. В нём самоконтроль усиливается чётностью функции – график симметричен относительно оси 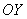, и если в вашем исследовании что-то противоречит данному факту, ищите ошибку.

Чётную или нечётную функцию можно исследовать только при 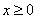, а потом пользоваться симметрией графика. Такое решение оптимально, однако выглядит, по моему мнению, весьма непривычно. Лично я рассматриваю всю числовую ось, но дополнительные точки нахожу всё же лишь справа:

Провести полное исследование функции и построить её график.

Решение: понеслась нелёгкая:

1) Функция определена и непрерывна на всей числовой прямой: .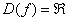

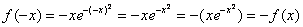
, значит, данная функция является нечетной, её график симметричен относительно начала координат.

Очевидно, что функция непериодическая.

2) Асимптоты, поведение функции на бесконечности.

Так как функция непрерывна на 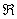, то вертикальные асимптоты отсутствуют

Для функции, содержащей экспоненту, типично раздельное исследование «плюс» и «минус бесконечности», однако нашу жизнь облегчает как раз симметрия графика – либо и слева и справа есть асимптота, либо её нет. Поэтому оба бесконечных предела можно оформить под единой записью. В ходе решения используем правило Лопиталя:

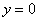
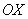
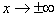
Прямая (ось ) является горизонтальной асимптотой графика при .

Обратите внимание, как я хитро избежал полного алгоритма нахождения наклонной асимптоты: предел 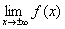вполне легален и проясняет поведение функции на бесконечности, а горизонтальная асимптота обнаружилась «как бы заодно».

Из непрерывности на 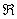и существования горизонтальной асимптоты следует тот факт, что функция ограничена сверху и ограничена снизу.

3) Точки пересечения графика с координатными осями, интервалы знакопостоянства.

Здесь тоже сокращаем решение:
График 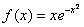проходит через начало координат.

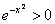
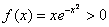
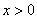
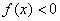
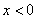
Других точек пересечения с координатными осями нет. Более того, интервалы знакопостоянства очевидны, и ось можно не чертить: , а значит, знак функции зависит только от «икса»:
, если ;
, если .

! Настоятельно рекомендую оформлять черновой шаблон графика
по ходу исследования!

4) Возрастание, убывание, экстремумы функции.

– критические точки.

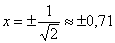
Точки симметричны относительно нуля, как оно и должно быть.

Определим знаки производной:

Функция возрастает на интервале 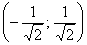и убывает на интервалах

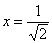
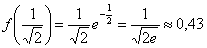
В точке функция достигает максимума: .

В силу свойства 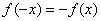(нечётности функции) минимум можно не вычислять:

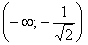
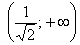
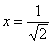
Поскольку функция убывает на интервале , то, очевидно, на «минус бесконечности» график расположен под своей асимптотой. На интервале функция тоже убывает, но здесь всё наоборот – после перехода через точку максимума линия приближается к оси уже сверху.

Из вышесказанного также следует, что график функции является выпуклым на «минус бесконечности» и вогнутым на «плюс бесконечности».

После этого пункта исследования прорисовалась и область значений функции:

Если у вас возникло недопонимание каких-либо моментов, ещё раз призываю начертить в тетради координатные оси и с карандашом в руках заново проанализировать каждый вывод задания.

5) Выпуклость, вогнутость, перегибы графика.

– критические точки.

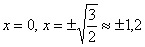
Симметрия точек сохраняется, и, скорее всего, мы не ошибаемся.

Определим знаки :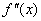

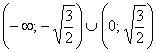
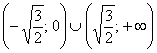
График функции является выпуклым на и вогнутым на .

Выпуклость/вогнутость на крайних интервалах подтвердилась.

Во всех критических точках существуют перегибы графика. Найдём ординаты точек перегиба, при этом снова сократим количество вычислений, используя нечётность функции:

6) Дополнительные точки целесообразно рассчитать только для правой полуплоскости:

Выполним чертёж: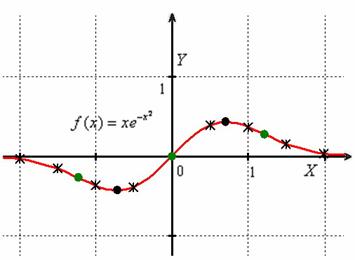

Такой вот симпатяга….

Изначально было запланировано 5 примеров, и если честно, я ожидал, что статья получится заметно больше по объему. Конечно, хочется исследовать ещё одну функцию, но с другой стороны – нельзя объять необъятное, поэтому сегодня воздержимся от логарифмов. Самое важное – усвоить методы, приёмы и хитрости исследования, которые мы только что разобрали.

Желающие могут пройти на страницу готовых задач по высшей математике и закачать архив, который содержит 69 исследований. Выбирайте любую функцию и тренируйтесь! А кто знает…, может встретите ту единственную, которую так давно искали =)

Пример 2: Решение: проведём исследование функции:
1) Функция определена и непрерывна на всей числовой прямой, .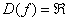

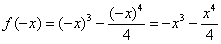
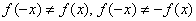
, значит, данная функция не является четной или нечетной.
Функция непериодическая.

2) Асимптоты графика, поведение функции на бесконечности.
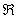
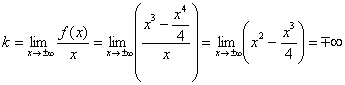
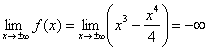
Так как функция непрерывна на , то вертикальные асимптоты отсутствуют.
, значит, наклонные асимптоты также отсутствуют.
, функция не ограничена снизу.

3) Точки пересечения графика с координатными осями, интервалы знакопостоянства функции.
График 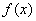проходит через начало координат.
С осью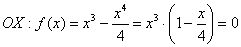

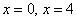
Определим знаки :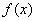

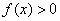
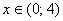
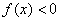
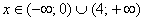
, если ,
, если .

4) Возрастание, убывание, экстремумы функции.

– критические точки.
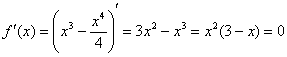
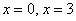
Определим знаки :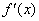

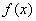
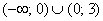
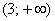
возрастает на и убывает на .
В точке 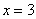функция достигает максимума:

5) Выпуклость, вогнутость, перегибы графика.

– критические точки.
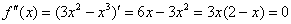
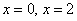
Определим знаки :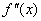

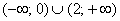
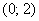
График функции является выпуклым на и вогнутым на .
В обеих критических точках существуют перегибы графика.

6) Найдем дополнительные точки:

Выполним чертёж:

Пример 4: Решение: проведем исследование функции:

1) Функция определена и непрерывна на всей числовой прямой, .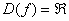

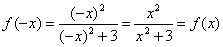
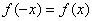
, значит, данная функция является четной, ее график симметричен относительно оси ординат.
Очевидно, что функция непериодическая.

2) Асимптоты, поведение функции на бесконечности.
Так как функция непрерывна на всей числовой прямой, то вертикальные асимптоты отсутствуют.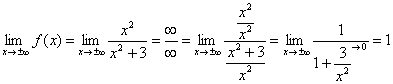

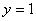
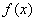
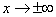
Прямая является горизонтальной асимптотой для графика при .

3) Точки пересечения графика с координатными осями, интервалы знакопостоянства функции.
График функции проходит через начало координат.
на всей области определения.

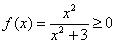
4) Возрастание, убывание, экстремумы функции.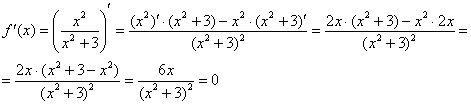

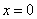
– критическая точка.
Определим знаки :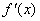

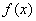
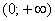
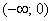
возрастает на и убывает на .
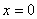
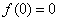
В точке функция достигает минимума: .

5) Выпуклость, вогнутость, перегибы графика.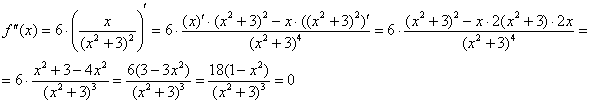

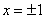
– критические точки.
Определим знаки :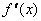

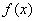
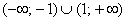
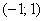
График является выпуклым на и вогнутым на .
В обеих критических точках существуют перегибы графика: .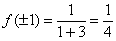

6) Найдем дополнительные точки и выполним чертёж:

Автор: Емелин Александр

(Переход на главную страницу)

Zaochnik.com – профессиональная помощь студентам

Источник