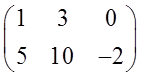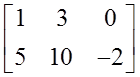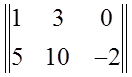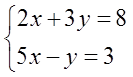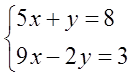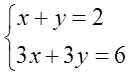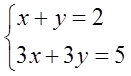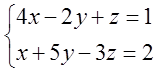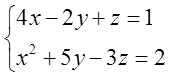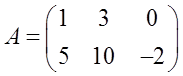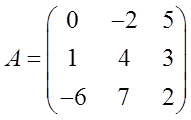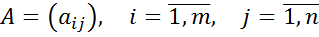Итая житая что такое
Народ, стоит здесь задавать вопрос по эонометрике?
Для просмотра формул ваш браузер должен поддерживать MathML.
| Объявления | Последний пост | |
|---|---|---|
 | Senior lecturer in Mathematics Linkoping (Швеция) | 04.09.2021 23:16 |
 | Работа автором топиков и проектов на математическом треке Hyperskill | 24.09.2021 21:18 |
 | Postdoc: Stochastics and algorithmics behind network problems (Netherlands) | 08.10.2021 08:36 |
Привет всем умникам и умницам.
Помогите до делать 3 задания по эконометрике:
1)Вычислить эмпирическое корреляционное отношение и оценить его значимость на 5% уровне.
2)На уровне значимости (альфа)=0.05 проверить гипотезу о линейной корреляционной зависимости между переменными Y и X.
3)Найти уравнение прямых регрессии построить их график на корреляционном поле и найти 95% доверительный интервалы для коэффициентов регрессии.
Если кто-то захочет помочь скажите я и вышлю данные.
Если вы спросите почему я сам не делаю? Всё потому что не хватает времени, очень много экзаменов и по др.дисциплинам.
Переменные с индексами



В математике широко применяются так называемые индексированные переменные. На бумаге они записываются так:
а читаются так: икс первое, икс второе, бэ восьмое, игрек итое, игрек и минус шестое, зет итое житое, зет и плюс первое житое. Поскольку в алфавите Паскаля нет подстрочных букв и цифр, то те же индексированные переменные на Паскале приходится обозначать так:
X[1] X[2] B[8] Y[i] Y[i-6] Z[i,j] Z[i+1,j]
Зачем нужны индексированные переменные? Их удобно применять хотя бы при операциях над числовыми рядами. Числовой ряд – это просто несколько чисел, выстроенных по порядку одно за другим. Чисел в ряду может быть много и даже бесконечно много.
Возьмем, например, бесконечный ряд чисел Фибоначчи: 1 1 2 3 5 8 13 21 34. Попробуйте догадаться, по какому закону образуются эти числа. Если вы сами не догадались, то я подскажу: каждое из чисел, начиная с третьего, является суммой двух предыдущих. А теперь попробуем записать это утверждение с помощью языка математики. Для этого обозначим каждое из чисел Фибоначчи индексированной переменной таким образом:
Первое число Фибоначчи обозначим так: f[1],
Второе число Фибоначчи обозначим так: f[2] и т.д.
Очевидно, что f[3]=f[1]+f[2],
Как математически одной формулой записать тот факт, что каждое из чисел является суммой двух предыдущих? Математики в индексном виде это записывают так:
Для иллюстрации подставим вместо i любое число, например, 6. Тогда получится:
Задание 102: Запишите в индексном виде, как получается из предыдущего числа ряда последующее:
Что такое матрица? Понятие матрицы.
Но высшая математика на то и высшая, что работает с более сложными объектами, чем привычная школьная. От этого никуда не деться.) И матрица — один из первых таких объектов, с которым студенты знакомятся уже на первом курсе ВУЗа. И мы тоже познакомимся.)
Итак, ключевые причины, почему же студенты не любят матрицы и всячески стараются избегать работы с ними. Перечислю их.
Причина первая — визуальное восприятие. Оно… непривычно, да.) С формулами, уравнениями, графиками у народа обычно всё более-менее ясно и прозрачно: в школе всё худо-бедно решалось, строилось, ощущалось. Всё знакомо. А тут… Какая-то табличка, какие-то малопонятные буковки с индексами (аж двумя!), которые так и норовят путаться перед глазами. Всё это поначалу очень смущает и даже пугает, да…
Причина вторая — это действия с матрицами. Их очень и очень много. Сложение матриц, умножение матриц, транспонирование матриц, поиск обратной матрицы, вычисление определителя, вычисление миноров матрицы, ранга матрицы… Причём все эти операции тоже весьма специфичны и имеют очень мало общего с действиями над обычными числами и алгебраическими выражениями из школьной математики. Эти фишки тоже очень здорово выбивают из колеи.
Причина третья — это рутина. Спору нет, работа с матрицами порой бывает весьма занудной. И скучной. А вместе с рутиной неизбежно возрастает и вероятность глупых арифметических ошибок, да… Особенно при работе с матрицами больших размерностей и/или в процессе элементарных преобразований. Где-то минус теряется, где-то вместо нуля единица пишется, где-то 3+4 двенадцать получается… Эти ляпы на общем фоне рутинной работы просто-напросто не замечаются. И лечатся только лишь предельным вниманием. К сожалению.
И даже после прочтения всех этих ужасов отчаиваться и впадать в панику рано. Прорвёмся!) Для начала успокою: матрица сама по себе — понятие очень простое. Да-да! И главное — полезное и очень мощное в высшей математике. Такое же полезное и мощное, как, скажем, формулы сокращённого умножения в школьной алгебре.) Сомневаетесь? Не надо.) Всё сами дальше увидите. Нужно лишь собраться с духом, рискнуть и… почитать.)
Итак, начнём с первой проблемы — с визуального восприятия.)
Что такое матрица? Устройство матрицы.
Так что же такое матрица? Нет, ничего общего с известным американским научно-фантастическим боевиком данное понятие не имеет. Ну… очень-очень отдалённое сходство всё же есть.)
Итак, удивляемся, но запоминаем:
Матрица — это просто прямоугольная таблица каких-либо элементов.
И всё! Ничего хитрого за этим страшным понятием больше не кроется.) Разумеется, каждое слово в определении несёт свой собственный смысл, да. Разберёмся?)
Слова “прямоугольная таблица” вопросов ни у кого не вызывают (надеюсь).
Например, можно сочинить что-нибудь типа такого:
Чем не прямоугольная табличка?) Но матрицы в высшей математике изображаются и выглядят немножко по-другому, нежели то что мы называем таблицей в привычном восприятии.
Чаще всего матрица в математике записывается вот так:
Всё очень просто и компактно, правда? Никаких рамок, никаких ячеек — ничего чертить и рисовать не нужно. Любая матрица записывается просто набором каких-то чисел в скобочках. Скобочки, кстати, могут быть не только круглыми. Могут быть и квадратными:
Или даже в виде вот таких двойных прямых палочек:
Это всё одно и то же. В большинстве учебников обычно используются круглые скобки. Квадратные скобки чаще встречаются в технических дисциплинах — в сопромате, строительной механике, теории упругости и т.п. Двойные — почти нигде не встречал. Я всё-таки буду следовать традициям и рисовать круглые скобки. Надеюсь, возражений нет.)
Итак, с таблицей разобрались. Что же такое “элемент”? Тоже элементарно (сорри за тавтологию). Любое число, стоящее в матрице на определённом месте, и будет её элементом! Для нашей матрицы число 1 — элемент, 5 — тоже элемент, и 10 — тоже элемент. В общем, вы поняли…
Кстати, слова “на определённом месте” я выделил не зря. И вот почему. Дело всё в том, что любую матрицу следует воспринимать именно как таблицу! А вовсе не как простое множество или набор чисел. Поясняю в чём суть. Рассматривая простое множество чисел, скажем, <1; 2; 3>, мы имеем полное право переставлять элементы множества как попало.
Например, мы можем переставить единичку и двойку. Получим:
Или переставить двойку и тройку:
И так далее. Перестановки элементов множества на его сути никак не сказываются. А вот матрицы более чувствительны к перестановкам. И переставлять элементы матрицы просто так нельзя! Каждый элемент строго на своём месте, в своей ячейке. И если переставить местами хотя бы два элемента, то получится, вообще говоря, уже другая матрица. С другими свойствами, да.
Элементами матрицы, кстати, могут быть не только числа. Могут быть и буквенные выражения, и даже функции. Всякое может быть.) Матрицы с функциями в качестве элементов так и называются — функциональными. Это — довольно сложная штука. И встречается уже в серьёзных разделах высшей математики — в дифференциальных уравнениях, в теории функций нескольких переменных и т.п. Этих ужасов пока не будет.)
Мы же пока будем работать только с матрицами, элементами которых являются числа. Или с числовыми матрицами. Намёк понятен?)
Откуда взялись матрицы, зачем они нужны и в чём их смысл?
Итак, мы выяснили, что матрица — это какая-то табличка. Чаще всего с какими-то числами. Ну и что из этого — спросите вы? Табличка и табличка… Что с ней делать-то? Просто пучить глазки? А делать можно очень много полезного! В соответствующих уроках сами увидите.)
На самом деле с матрицами вы постоянно сталкивались ещё в школе. Сами того не подозревая. Не верите? Сейчас удивитесь.)
Слова “система уравнений” вам знакомы?
Например, такая простенькая системка из двух линейных уравнений:
Решив её (например, подстановкой), получим ответ:
Или, кратенько: (1; 2).
Можно изменить коэффициенты при икс и игрек и получить какую-то новую систему. Например, такую:
Решив её, получим новый ответ: (1; 3).
А можно, например, коэффициенты при переменных не трогать, зато как-то поменять свободные члены. Вместо 8 и 3 записать, скажем, 1 и 2. Получим снова какую-то систему и какое-то решение…
Короче говоря, меняя в системе уравнений коэффициенты при неизвестных и/или свободные члены, можно получать какие-то решения для конкретной системы. Для каждого набора чисел — свои. Кстати, можно и такое наподбирать, что система вообще не будет иметь решений или будет иметь бесконечно много решений.)
Эта система имеет бесконечно много решений. И (1; 1) — решение, и (0; 2) — решение, и (0,5; 1,5) — тоже решение. Можно перечислять до посинения…)
А теперь я изменю в этой системе всего одно число и получу систему, которая вообще не имеет решений:
Кому интересно, можете решить подстановкой. Получите забавный результат 6=5. Попробуйте.)
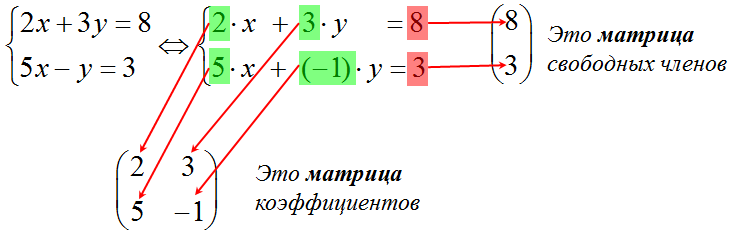
Итак, что мы видим? Мы видим, что решение системы колоссальным образом зависит от этого самого набора чисел. Причём только от него! Этот факт настолько важен, что математики даже придумали этот самый набор чисел (коэффициентов и свободных членов системы) оформлять в виде таблички. Или, говоря математическим языком, в виде матрицы.
Меняя содержимое табличек (матриц) коэффициентов и свободных членов, мы будем получать различные системы линейных уравнений. С различными решениями, да.)
Кстати, вот вам и ответ на вопрос, почему мы не можем просто так переставлять элементы в матрице. Не догадались? Да! Переставив местами хотя бы два элемента, мы получим уже другую матрицу, соответствующую другой системе уравнений. И с другими решениями…
Ну ладно, системы из двух уравнений — это ещё легко. При их решении про матрицы можно особо не вспоминать: выражай себе по-школьному икс через игрек (или наоборот), делай подстановку, решай — и дело с концом. А вот система из трёх линейных уравнений с тремя неизвестными уже гораздо злее.) Заниматься явным выражением одной переменной через другую, подстановкой и прочим школьным занудством уже неохота, да… А если уравнений и/или неизвестных ещё больше? Скажем, четыре или пять…)
И вот тут возникает вполне закономерный вопрос: а можно ли, как-то работая напрямую только с матрицами (коэффициентов и свободных членов), попробовать выяснить:
1) Есть у системы решение или нет его? Или решений вообще бесконечно много?
2) Если решение есть и единственно, то отыскать его быстро и легко.
Новость хорошая: да, можно! Добро пожаловать в новый раздел высшей математики! Под названием линейная алгебра.)
Именно этот раздел и занимается решением систем линейных алгебраических уравнений. Сокращённо — СЛАУ.) Эта страшная аббревиатура будет мозолить вам глаза на протяжении почти всех уроков этого раздела. Привыкаем.)
Причём прошу обратить особое внимание на слово “линейных”. Это слово означает, что все неизвестные (x, y, z, …) входят во все уравнения максимум в первой степени и нигде не должно быть деления на неизвестное.
Это система двух линейных алгебраических уравнений (СЛАУ) с тремя неизвестными. Все неизвестные (x, y, z) в только первой степени, деления на неизвестное ни в одном из уравнений нету. То что число неизвестных больше числа уравнений — вопрос другой. В соответствующем уроке мы научимся с такими злыми системами расправляться.) Главное, что оба уравнения — линейные. Это важно.)
А теперь я изменю в этой системе всего одно слагаемое. Нарисую, например, квадратик над иксом во втором уравнении:
А вот такая система уравнений будет уже нелинейна, да… Именно из-за этого самого квадратика, нарушающего базовый принцип “все неизвестные только в первой степени”. К нелинейным системам имеется свой индивидуальный подход, и линейная алгебра перед ними бессильна… С такими системами мы в этом разделе работать не будем. На радость студентам.)
Матрицы — очень мощный инструмент для решения систем линейных алгебраических уравнений (СЛАУ).
Но не одними лишь системами уравнений ограничивается применение матриц! Матрица — это ещё и своего рода математический оператор. Или преобразователь. Который что-то куда-то преобразует. Или отображает. Как фотоаппарат.) Скажем, один вектор через матрицу можно отобразить в другой. Мощная штука.) Об этом в более серьёзных темах линейной алгебры будет. А системы — так, частный случай. Для начального знакомства.
Как обозначать матрицу и её элементы?
Очень просто. Любые матрицы в математике обозначаются большими буквами латинского алфавита: A, B, C и так далее.
Например, нашу матрицу, приведённую в начале урока, можно обозначить вот так:
И все дела. Слева от знака равенства — название матрицы, справа — её содержимое. В скобочках.)
Но это ещё не все обозначения. Есть и другие, более специфические. Разберём и их.
Любая матрица — это ведь табличка, не так ли? А из чего у нас состоит любая табличка? Правильно, из строчек и колонок! Только это в обиходе.) А в математике те же самые названия звучат более научно — строки и столбцы! Зацените.)
Количество этих самых строк и столбцов коротко записывают в виде произведения m x n и называют размерностью матрицы. Которая дополнительно может указывается в виде подстрочного знака.
Читается эта запись очень просто: “матрица A размерности m на n”. И вот тут студентов могут подстерегать первые проблемы. Какое число (буква) за что отвечает?
Запоминаем:
В размерности матрицы m x n первое число (m) — это (всегда!) количество СТРОК в матрице. Второе число (n) — количество СТОЛБЦОВ.
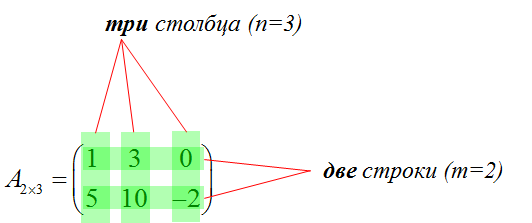
Именно в таком порядке. Сначала строки, а потом — столбцы. А не наоборот. Например, наша матрица — это матрица размера “два на три”:
У неё две строки (m=2) и три столбца (n=3).
Размерность — ключевая характеристика любой матрицы. Почему? А потому, что на некоторые операции с матрицами (например, на сложение, умножение, взятие определителя и обратной матрицы) существуют очень жёсткие ограничения по размерности! Сами увидите. В соответствующих уроках.)
А как кратко в общем виде обозначать элементы матрицы? Тоже просто. Маленькими латинскими буквами с двойным индексом.
И всё. Читается эта закорючка так: “а и-жи”. Или: “а итое-житое”. Забавно, да? Тем не менее вполне себе научно.)
И снова могут быть проблемы с расшифровкой индексов. В школе ведь мы привыкли работать с одиночными индексами. В прогрессиях, например. А тут — двойной! Какой индекс что означает? Не беда! Принцип расшифровки индексов тот же самый — сначала строка, а потом столбец. Первый индекс “i” (“и”)– это номер строки, где находится интересующий нас элемент. Второй индекс “j“ (“жи”) – номер столбца.
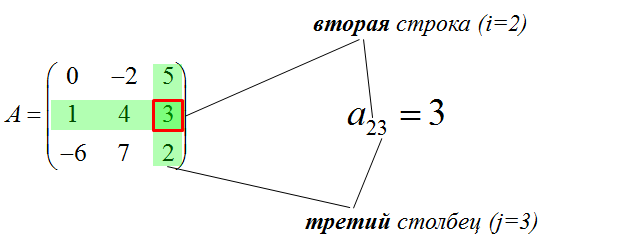
Например, нам дана такая матрица A:
Здесь первый индекс “и” равен двойке (i=2), а второй индекс “жи” – тройке (j=3). Вот и пересекаем (мысленно!) вторую строку и третий столбец. На пересечении получаем нужный нам элемент a23 = 3.
Точно так же на пересечении первой строки и первого столбца мы получим элемент матрицы a11 = 0, на пересечении третьей строки и второго столбца — элемент a32 = 7 и так далее. Чем-то похоже на игру в кораблики или морской бой, не находите?) Вроде бы, всё элементарно. И что, думаете не ошибаются люди? Ошибаются, ещё как! Ещё один источник дурацких ошибок при работе с элементами матриц — это неправильная нумерация строк и столбцов. Со столбцами обычно всё ясно — нумеруем и читаем привычно, слева направо. Не арабы, чай…) А вот со строками могут случаться и непонятки — сверху вниз их нумеровать или снизу вверх…
Запоминаем:
В элементе матрицы aij первый индекс (i) — номер строки, второй индекс (j) — номер столбца. Нумерация строк (всегда!) — сверху вниз. Нумерация столбцов (всегда!) — слева направо.
А теперь, разобравшись с загадочными индексами i и j, мы подходим к самому научному способу задания матрицы — через элемент матрицы в общем виде и диапазон изменения индексов.
Вот она, эта запись:
Расшифровываются эти страшные иероглифы так:
Задана матрица А с элементами aij , где индекс “i” принимает все натуральные значения от единицы до “эм” включительно, а индекс “j” — все натуральные значения от единицы до “эн” включительно.
Солидно, да… Куда проще не заморачиваться и написать кратко и точно Amxn, правда? Но будьте готовы и к такой супернаучной форме записи. Особенно в каких-нибудь продвинутых учебниках.)
Внимание! Запись элемента a23 читается и произносится как “а два три“. Именно так, вы не ослышались.) Ни в коем случае не “a двадцать три“! Или b11 — это элемент “бэ один один“ (а не “бэ одиннадцать“ )! Такое чтение — это… гм… серьёзный вызов преподавателю.) И говорит о полном отсутствии хоть какого-то понимания. О “зачёте” (или “удовл”) даже и не мечтайте после этого. Вот так.
Порядок проведения и математической обработки результатов статистических измерений
При измерениях одного и того же размера в выборке, так же как и во всей партии деталей измеренные значения несколько отличаются друг от друга. Если количество измерений в выборке невелико, то для определения доверительного интервала более полного разброса их значений необходимо провести статистическую обработку результатов измерений.
Статистическая обработка результатов измерений производится следующим образом.
Имеются следующие исходные данные:
номинальный размер детали Х и его допуск T, на чертеже обозначаемые как Х±Т;
N – количество измеренных деталей, один и тот же размер которых несколько отличается между собой по величине или равный у некоторых деталей. Обычно в исходных данных задачи результаты измерений записаны в хаотическом порядке.
Решение
1) Располагают полученные в процессе N измерений действительные значения Xi в порядке возрастания их величины и тем самым получают ранжированный ряд случайных дискретных величин: X1; X2…XN.
2) Диапазон рассеивания R определяется как разность между максимальной XMAX и минимальной XMIN величинами действительных значений измерений:
3) Полученное значение диапазона рассеивания разбивают на K интервалов (рекомендуется 7 – 12 интервалов). Задавшись числом интервалов, рассчитывают дискретный шаг интервалов по формуле:
Полученный отрезок оси делят на K равных по длине интервалов и записывают напротив каждой границы её числовое значение: X1; X1+P; (X1+P)+P и так далее. Конечное значение должно совпасть с XN.
5) Для каждого интервала подсчитывают число измерений nj, имеющих величину, находящуюся в пределах между меньшей, например, X1 и большей X1+P границами этого интервала и так далее.
6) После этого для каждого интервала рассчитывают среднее арифметическое значение X jСР в группе измерений j-того интервала, а также частость числа измерений
nj /(N – 1) в данном интервале.
Результаты измерений и расчётов пунктов 1), 5) и 6) заносят в таблицу.
Пример таблицы с записями значений случайной величины при N=16 и К=7 приведён в таблице 3.1 (вместо букв «ранжированный ряд» надо поставить измеренные величины по возрастанию X1; X2…X16. В первый интервал вошли X1 и X2, во второй – X3, X4 и X5. И так далее для каждого интервала.
Таблица 3.1 – Записи значений случайной величины Xi (ИТОЕ)
| Номер измерения | ||||||||||
| Хi (ИТОЕ) | р | а | н | ж | и | р | о | в | а | н |
| X jСР (ЖИТОЕ) | (р+а)/2 | (н+ж+и)/3 | (р+о+в+а+н)/5 | |||||||
| nj (ЖИТОЕ) | ||||||||||
| nj /(N – 1) | 2/15 | 3/15 | 1/3 |
Продолжение таблицы 3.1
| Номер измерения | ||||||
| Xi (ИТОЕ) | н | ы | й | р | я | д |
| X jСР (ЖИТОЕ) | (н+ы)/2 | (й+р+я+д)/4 | ||||
| nj (ЖИТОЕ) | ||||||
| nj /(N – 1) | 2/15 | 4/15 |
где Xi – значение i-того измерения;
nj – число измерений, имеющих величину, находящуюся в пределах между меньшейи большей границами j-того интервала;
nj /(N – 1) – частость числа измерений в данном интервале.
X jСР – среднее арифметическое значение измерений j-того интервала (рассчитывается для каждого интервала):
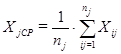
Хij – (икс итое-житое) – измерение Xi в j-том интервале, то есть находящееся в пределах между меньшейи большей границами j-того интервала;
nj /(N – 1) – частость числа измерений в данном интервале.
В таблице в приведенном примере всего 5 размерных интервалов вместо 7 потому что, например, в двух интервалах значений размеров не оказалось: в первом интервале – 2 значения измерений (1 и 2), во втором – 3 (3, 4 и 5) и так далее, а в четвёртом и шестом, например, их нет. Пустые интервалы в таблице не указываются.
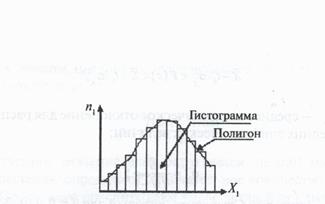
7) Над каждым интервалом строят прямоугольник, соответствующий по своей высоте величине рассчитанной частости nj /(N – 1) для этого интервала, после чего строят эмпирическую ломаную кривую, соединяя серединки верхних перекладин прямоугольников. Если в каком-то интервале частость равна нулю, то ломаную кривую соединяют с серединкой интервала на оси абсцисс.
8) Определяют среднее арифметическое значение всех замеренных действительных значений величин:
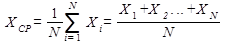
Рисунок – Пример построения гистограммы
9) Рассеяние значений случайных величин в выборке из N измерений относительно эмпирического (опытного, практического) группирования их по интервалам характеризуется уточнённым эмпирическим средним квадратическим отклонением, которое определяется по формуле:

10) По результатам выборки устанавливают границы, внутри которых с определённой вероятностью будет находиться математическое ожидание F(x) случайной величины Х. Эти границы определяют доверительный интервал, который зависит от доверительной вероятности β. В общем случае при малой выборке и различной доверительной вероятности доверительный интервал в своих меньшей и большей границах выразится следующими неравенствами:
ХСР – tδσх ср 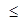
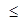
где σх ср – среднее квадратическое отклонение для распределения средних арифметических величин:
σх ср 
tδ – критерий Стьюдента, который для β=0,9 (90% доверительная вероятность) принимаем равным 1,75.
11) Сравнивают границы доверительного интервала с допуском на размер (он задан в условии задачи) и делают вывод о годности всей партии деталей. Для сравнения строят в примерном масштабе схему поля допуска заданного размера X и рядом наносят поле доверительного интервала.
Если границы доверительного интервала не выходят за пределы поля допуска, то партия деталей считается годной с доверительной вероятностью β.
12) Ответом на решение задачи является вывод о годности партии деталей: партия деталей годна или не годна с указанием сравниваемых величин большей и меньшей границ доверительного интервала и верхней и нижней границ поля допуска детали.
Условие задачи
В партии одинаковых деталей у каждой из них измеряется один и тот же размер. Так как количество деталей в выборке для измерений невелико, то для определения доверительного интервала более полного разброса значений размера необходимо провести статистическую обработку результатов измерений.
Изготовлена большая партия круглых стержней и из неё сделана выборка в количестве N=16 штук. Измерен диаметр каждого стержня d1, d2…dN. Для определения годности всей большой партии деталей необходимо построить гистограмму и провести статистическую обработку результатов измерений деталей в выборке.
Исходные данные:N=16 штук – количество стержней; d±IT мм – номинальный диаметр стержня d (из таблицы 3.2) с допуском IT на изготовление (из таблицы 3.3); размерный неранжированный ряд: d1; d2. d16 (из таблицы 3.2).
произвести измерения и занести полученные значения случайных величин в таблицу;
построить гистограмму и эмпирическую кривую (полигон) распределения размеров стержней в партии;
определить доверительный интервал значений измерений диаметров стержней;
сделать заключение о годности всей партии стержней путём сравнения границ доверительного интервала с величиной поля допуска номинального размера.
Варианты номинальных диаметров стержней и результатов измерений выборки из партии выбираются по последней цифре учебного шифра из таблицы 3.2, варианты величины допуска на размер – по предпоследней цифре учебного шифра из таблицы 3.3.
Таблица 3.2 – Варианты номинальных диаметров стержней деталей и результатов измерений выборки из партии, мм
| №вар ианта | d | Номер и результат измерения | |
| d1 | d2 | d3 | d4 |
| 24,85 | 24,90 | 24,90 | 25,02 |
| 27,86 | 27,91 | 27,91 | 28,10 |
| 31,87 | 31,92 | 31,92 | 32,05 |
| 39,88 | 39,93 | 39,93 | 40,07 |
| 44,89 | 44,94 | 44,94 | 45,08 |
| 49,85 | 49,90 | 49,90 | 50,01 |
| 55,86 | 55,91 | 55,91 | 56,02 |
| 62,87 | 62,92 | 62,92 | 63,03 |
| 70,88 | 70,93 | 70,93 | 71,06 |
| 79,89 | 79,94 | 79,94 | 80,07 |
Продолжение таблицы 3.2
| №вар ианта | d | Номер и результат измерения | |
| d5 | d6 | d7 | d8 |
| 25,02 | 25,10 | 25,10 | 25,10 |
| 28,10 | 28,15 | 28,15 | 28,15 |
| 32,05 | 32,12 | 32,12 | 32,12 |
| 40,07 | 40,13 | 40,13 | 40,13 |
| 45,08 | 45,14 | 45,14 | 45,14 |
| 50,01 | 50,15 | 50,15 | 50,15 |
| 56,02 | 56,10 | 56,10 | 56,10 |
| 63,03 | 63,12 | 63,12 | 63,12 |
| 71,06 | 71,14 | 71,14 | 71,14 |
| 80,07 | 80,15 | 80,15 | 80,15 |
Продолжение таблицы 3.2
| №вар ианта | d | Номер и результат измерения | |
| d9 | d10 | d11 | d12 |
| 24,86 | 24,89 | 24,99 | 25,03 |
| 27,88 | 27,90 | 27,99 | 28,01 |
| 31,89 | 31,91 | 32,02 | 32,03 |
| 39,87 | 39,92 | 39,98 | 40,03 |
| 44,88 | 44,93 | 44,98 | 45,01 |
| 49,86 | 49,91 | 49,97 | 50,02 |
| 55,87 | 55,92 | 55,99 | 56,03 |
| 62,88 | 62,93 | 62,98 | 63,04 |
| 70,87 | 70,91 | 70,97 | 71,04 |
| 79,87 | 79,93 | 79,99 | 80,01 |
Продолжение таблицы 3.2
| №вар ианта | d | Номер и результат измерения | |
| d13 | d14 | d15 | d16 |
| 25,04 | 25,03 | 25,11 | 25,11 |
| 28,03 | 28,05 | 28,14 | 28,13 |
| 32,05 | 32,02 | 32,13 | 32,14 |
| 40,02 | 40,03 | 40,14 | 40,12 |
| 45,03 | 45,04 | 45,13 | 45,11 |
| 50,04 | 50,03 | 50,16 | 50,16 |
| 56,01 | 56,05 | 56,12 | 56,13 |
| 63,02 | 63,01 | 63,13 | 63,14 |
| 71,03 | 71,01 | 71,15 | 71,15 |
| 80,02 | 80,04 | 80,16 | 80,12 |
Таблица 3.3 – Варианты величины допуска на размер, мм
| № вари- анта | ||||||||||
| IT | ±0,11 | ±0,12 | ±0,13 | ±0,14 | ±0,15 | ±0,16 | ±0,17 | ±0,18 | ±0,19 | ±0,10 |
Задача 4
Тема: «Штриховое кодирование информации о товаре»
Теоретическая часть
Штриховое кодирование стало впервые применяться в США для идентификации железнодорожных вагонов и, вследствие этого в промышленности и торговле появился универсальный товарный код (URC), состоящий из 12 знаков.
В 1977году по примеру американской была принята европейская система кодирования товаров (EAN – European Article Nambering) как разновидность кода URC для Европы, отличаясь только тринадцатым знаком. В европейской системе кодирования для товаров из США тринадцатым знаком является ноль.
В настоящее время практически 100% продукции, выпускаемой в развитых странах мира для потребительского рынка, имеет на упаковке штриховой код EAN, определяющий производителя и товар.
Штриховой код – это чередование тёмных и светлых полос разной ширины. Носителями закодированной информации являются относительные ширины тёмных и светлых полос и их сочетания. Тёмные полосы называют штрихами, а светлые – пробелами. Ширина штрихов и пробелов всегда кратна модулю, равному по ширине самому узкому из них. Другие штрихи и пробелы составляют два или три модуля, то есть две или три толщины самого узкого штриха или пробела. Узкий штрих соответствует единице, а пробел – нулю в двоичной системе исчисления.
Штриховые коды делятся на товарные и технологические. Первые используются для идентификации производителей товаров и самих товаров, ими производимых. Вторые, с гораздо большим числом знаков – для передачи более подробной информации о производстве товара от производителя к другому производителю или оптовому поставщику для автоматизированного сбора информации и её последующей компьютерной обработки. Вторые могут располагаться на этикетке рядом с первыми, отличаясь шириной кода и количеством цифр.
Штриховые коды считываются специальными сканерами, которые, воспринимая штрихи, пробелы и их сочетания, декодируют штриховой код в цифровой и осуществляют ввод информации в ЭВМ.
Примеры штриховых кодов представлены на рисунках 1 и 2, примеры кодов некоторых стран – в таблице 4.
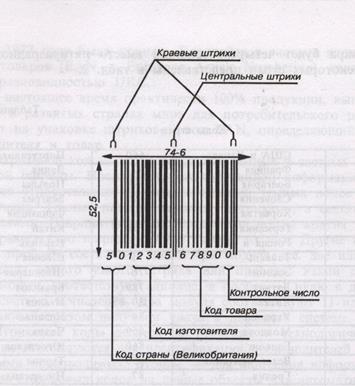
Рисунок 1 – Схема кода EAN-13
После кода страны следуют пять цифр кода изготовителя, который в РФ присваивает конкретному предприятию изготовителю товара национальный орган страны Внешнеэкономическая ассоциация автоматической идентификации ЮНИСКАН.
Последний 13-й разряд представляет собой контрольное число для проверки правильности считывания штрихового кода.
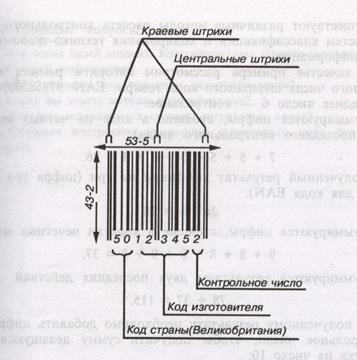
Если товар имеет небольшие размеры и площади, то из-за недостатка места для размещения штрихового кода на этикетке товара применяют 8-ми разрядный код EAN-8, который включает код страны, код изготовителя и контрольное число.
Рисунок 2 – Схема кода EAN-8
Числовые значения штрихового кода применяется для читки кода покупателем. Сканер его не считывает.
Контроль кода по величине контрольного числа необходим для проверки его правильности сканером по штрихам и покупателем по цифрам.
4.2 Методика расчёта правильности штрихового кода
1) Суммируют цифры, стоящие в коде на чётных местах.
2) Полученный результат умножают на три (множитель 3 принят для кодов EAN-13 и EAN-8).
3) Суммируют цифры, стоящие в коде на нечётных местах (без последнего контрольного числа).
4) Суммируют результаты двух последних действий.
5) Полученный результат суммируют с цифрой-контрольным числом. При правильном написании штрихового кода должно получиться число, кратное 10 (десяти)
Задание
По этикетке любого товара (кроме сигарет, алкогольных напитков, тетрадей и ручек), имеющей 13-значный штриховой код, определить следующие характеристики товара.
1) Наименование и модель товара (по надписи на этикетке).
2) Характеристики товара (по надписи на этикетке).
3) Страну, зарегистрированную на штриховом коде (по цифрам штрихового кода) сравнить с надписью на этикетке.
4) Предприятие-изготовитель (по надписи на этикетке) и соответствующие ему цифры кода (по цифрам штрихового кода).
5) Рассчитать правильность штрихового кода (по цифрам штрихового кода).