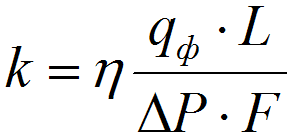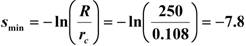Измерение коэффициента проницаемости пласта в чем измеряется
Добыча нефти и газа
Изучаем тонкости нефтегазового дела ВМЕСТЕ!
Проницаемость
Проницаемость – это фильтрующий параметр горной породы, характеризующий её способность пропускать через себя жидкости и газы при перепаде давления.
Абсолютно непроницаемых тел в природе нет. При сверхвысоких давлениях все горные породы проницаемы. Однако при сравнительно небольших перепадах давления в нефтяных пластах многие породы в результате незначительных размеров пор оказываются практически непроницаемыми для жидкостей и газов (глины, сланцы и т.д.).
Хорошо проницаемыми породами являются: песок, песчаники, доломиты, доломитизированные известняки, алевролиты, а так же глины, имеющие массивную пакетную упаковку (рис. 1.4).
Рис. 1.4. Пример массивной пакетной упаковки глин – фильтрация происходит через каналы между пакетами
Рис. 1.5. Пример упорядоченной пакетной упаковки глин – фильтрация практически не происходит
К плохо проницаемым относятся: глины, с упорядоченной пакетной упаковкой, глинистые сланцы, мергели, песчаники, с обильной глинистой цементацией (рис. 1.5).
1.3.1. Линейная фильтрация нефти и газа в пористой среде
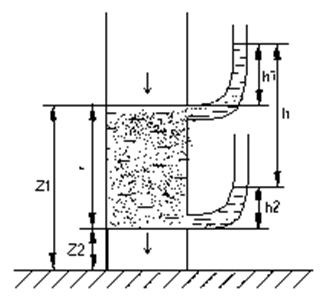
Для оценки проницаемости горных пород обычно пользуются линейным законом фильтрации Дарси. Дарси в 1856 году, изучая течение воды через песчаный фильтр (рис. 1.6), установил зависимость скорости фильтрации жидкости от градиента давления..
Рис. 1.6. Схема экспериментальной установки Дарси для изучения течения воды через песок
Согласно уравнению Дарси, скорость фильтрации воды в пористой среде пропорциональна градиенту давления:

где Q – объёмная скорость воды;
v – линейная скорость воды;
F – площадь сечения, F = pd2/4;
Нефть – неидеальная система (компоненты нефти взаимодействуют между собой), поэтому линейный закон фильтрации для нефти, содержит вязкость, учитывающую взаимодействие компонентов внутри нефтяной системы:

где m – вязкость нефти.
В этом уравнении способность породы пропускать жидкости и газы характеризуется коэффициентом пропорциональности k (1.7), который называется коэффициентом проницаемости (kпр).
Размерность коэффициента проницаемости (система СИ) вытекает из соотношения:

Размерность параметров уравнения Дарси в разных системах единиц
Площадь поперечного сечения фильтра, F
Перепад давления, ∆P
Вязкость жидкости, µ
В системе СИ коэффициент проницаемости измеряется в м2; в системе СГС [kпр] = см2; в системе НПГ (нефтепромысловой геологии) [kпр] = Д (Дарси).
1 Дарси = 1,02×10-8 см2 = 1,02 · 10-12 м2 » 1 мкм2.
Проницаемостью в 1 м2 называется проницаемость пористой среды при фильтрации через образец площадью 1 м2 длиной 1 м и при перепаде давления 1 Па, при которой расход жидкости вязкостью 1 Па×с составляет 1 м3.
Пористая среда имеет проницаемость 1 Дарси, если при однофазной фильтрации жидкости вязкостью 1 спз (спуаз) при ламинарном режиме фильтрации через сечение образца площадью 1 см2 и перепаде давления 1 атм., расход жидкости на 1 см длины породы составляет 1 см3/сек.
Физический смысл размерности проницаемости – это площадь сечения каналов пористой среды, через которые идет фильтрация.
Существует несколько типов каналов:
Приведённые выше уравнения справедливы при условии движения несжимаемой жидкости по линейному закону Дарси.
В случае фильтрации газа это условие не выполняется. При перепаде давления объём газа изменяется, и оценивается по закону Бойля-Мариотта:
При Т = const, P·V = const (1.10)
При линейной фильтрации газа оценивается средняя скорость фильтрации (Vср):
Vcр· Pср = Vо ·Pо = V1· P1 = V2 · P2, (1.11)
Pср = (P1 + P2) / 2, (1.12)
Vcр = Vо·Pо / Pср = 2·Vо·Pо / (P1 + P2). (1.13)
Тогда, средний объёмный расход газа будет равен:

Отсюда уравнение коэффициента проницаемости для газа:

1.3.2. Радиальная фильтрация нефти и газа в пористой среде
Процесс притока пластовых флюидов из пласта в скважину описывается моделью радиальной фильтрации. В этом случае образец породы представляется в виде цилиндрического кольца с проводящими каналами в осевом направлении (рис. 1.7).
Рис. 1.7. Схема радиального притока жидкости в скважину
Площадь боковой поверхности цилиндра: F=2prh, таким образом уравнение Дарси для радиальной фильтрации будет иметь следующий вид:

Отсюда, дебит при радиальной фильтрации жидкости:

Таким образом, коэффициент проницаемости при радиальной фильтрации:

1.3.3. Оценка проницаемости пласта, состоящего из нескольких пропластков различной проницаемости
Пласт состоит, как правило, из отдельных пропластков, поэтому общая проницаемость пласта (kпр) оценивается с учетом проницаемости пропластков и направления фильтрации.
Рис. 1.8. Линейная фильтрация в пласте, состоящем из нескольких изолированных пропластков различной мощности и проницаемости.
При линейной фильтрации жидкости в пласте, состоящем из нескольких изолированных пропластков различной мощности и проницаемости (рис. 1.8), средняя проницаемость пласта рассчитывается следующим образом:

где hi – мощность i-го пропластка;
ki – проницаемость i-го пропластка.
Рис. 1.9. Линейная фильтрация через пласт, имеющий несколько последовательно расположенных зон различной проницаемости.
При линейной фильтрации жидкости через пласт, имеющий несколько последовательно расположенных зон различной проницаемости (рис. 1.9), коэффициент проницаемости пласта рассчитывается следующим образом:

где Li – длина i-го пропластка;
ki – проницаемость i-го пропластка.
Рис. 1.10. Радиальная фильтрация через пласт, имеющий несколько концентрически расположенных зон различной проницаемости.
При радиальной фильтрации жидкости через пласт, имеющий несколько концентрически расположенных зон различной проницаемости (рис. 1.10), средняя проницаемость пласта оценивается следующим образом:

где rk – радиус контура;
rс – радиус скважины;
ri – радиус i-го пропластка;
ki – проницаемость i-го пропластка.
1.3.4. Классификация проницаемых пород
По характеру проницаемости (классификация Теодоровича Г. И.) различают коллектора:
По величине проницаемости (мкм2) для нефти выделяют 5 классов коллекторов:
1. очень хорошо проницаемые (>1);
2. хорошо проницаемые (0,1 – 1);
3. средне проницаемые (0,01 – 0,1);
4. слабопроницаемые (0,001 – 0,01);
Для классификации коллекторов газовых месторождений используют 1–4 классы коллекторов.
Проницаемость горных пород, коэффициент фильтрации, закон Дарси
Проницаемость горных пород
Способность горных пород пропускать через себя жидкости и газы называется проницаемостью. Любая горная порода при больших перепадах давлений может пропускать через себя жидкость или газ. Однако в условиях верхней части земной коры существуют породы, которые практически являются непроницаемы для жидкости и газа. К таким породам относятся плотные породы – соли, глины.
Классификация пустот в горных породах по размерам и форме (по М.К.Калинко,1964г.)
По морфологии пустот
Проницаемость, закон Дарси
Проницаемость определяет способность породы отдавать жидкости и газы, содержащиеся в них, при перепадах давлений. Еще в середине XIX века проводились опыты по определению скорости фильтрации воды в песках. На основе таких опытов французский ученый Дарси установил закон фильтрации, названный его именем – закон Дарси: скорость фильтрации прямо пропорционально гидравлическому уклону, обратно пропорционально длине пути фильтрации.
где h1, h2 – высоты над нулевым уровнем,
Δl – расстояние между точками измерения (длина пути фильтрации)
Гидравлический уклон 
Тогда закон Дарси принимает вид:

Эффективная пористость пород отсутствует при диаметре капилляров, равном 1 мкм. При диаметре каналов в десятые и сотые доли микрона струйное течение жидкости отсутствует, т.е. закон Дарси не соблюдается. Проникновение жидкости через такие породы происходит не по закону фильтрации, а по закону диффузии, т.е. на молекулярном уровне.
Определение проницаемости производится в лабораториях. Различают два вида проницаемости:
Проницаемость горных пород пласта
При относительно небольших перепадах давления в нефтяных пластах многие породы в результате незначительных размеров пор оказываются практически непроницаемыми для жидкостей и газов (глины, сланцы и т.д.).
Хотя при сверхвысоких давлениях все горные породы проницаемы.
Хорошо проницаемыми породами являются: песок, песчаники, доломиты, доломитизированные известняки, глины с массивной пакетной упаковкой, алевролиты.
Плохо проницаемыми породами являются: глины, с упорядоченной пакетной упаковкой, глинистые сланцы, песчаники с глинистой цементацией, мергели.
Различают также абсолютную, фазовую и относительную проницаемости.
Она зависит от размера и структуры поровых каналов, но не зависит от насыщающего флюида, т.е. характеризует физические свойства породы.
Обычно абсолютную проницаемость определяют при фильтрации азота через породу.
Для оценки проницаемости горных пород применяется открытый в 1856 г линейный закон фильтрации Дарси, который установил зависимость скорости фильтрации жидкости от градиента давления.
Абсолютную проницаемость определяют на основании закона Дарси по уравнению:
Проницаемость определяется как:
Существует несколько типов каналов:
Проницаемостью в 1 м 2 соответствует проницаемости горной породы при фильтрации через образец площадью 1 м2 длиной 1 м и при перепаде давления 1 Па, при которой расход жидкости вязкостью 1 Па*с составляет 1 м3.
Размерность параметров уравнения Дарси в разных системах единиц
Гидродинамические параметры пластов и скважин
Для решения многих практических задач, связанных с проектированием и разработкой НГМ, а также с установлением режимов эксплуатации отдельных скважин, необходимо определить параметры, характеризующие гидродинамические свойства скважин и пластов: продуктивность скважин, гидропроводность пласта, пьезопроводность пласта, коэффициент гидродинамического совершенства скважины.
Коэффициент продуктивности добывающей скважины — отношение ее дебита Q к перепаду между пластовым и забойным давлением, соответствующими этому дебиту — показывает на сколько может измениться дебит скважины при изменении депрессии на пласт на единицу:
 | (1.1) |
где, Q – дебит жидкости добывающей скважины, т/сут или м 3 /сут;
Рпл и Рс – соответственно давления пластовое и на забое скважины, МПа или атм, или кгс.
Размерности коэффициента продуктивности добывающей скважины:
В литературе обозначение коэффициента продуктивности добывающей скважины можно встретить через греческую букву η.
Из формулы Дюпюи для плоско-радиального притока однородной несжимаемой жидкости в одиночную добывающую скважину из кругового пласта коэффициент продуктивности добывающей скважины может быть определен как:
 | (1.2) |
где, k – проницаемость пласта, м 2 или Д;
h – мощность пласта, вскрытая добывающей скважиной, м;
μ – динамическая вязкость добываемой скважиной жидкости из пласта, Па·с, Пз;
Rk – радиус контура питания пласта или области дренирования добывающей скважины, м;
rc – радиус добывающей скважины по долоту, мм.
Для нагнетательной скважины определяют аналогичный коэффициент — коэффициент приемистости нагнетательной скважины:
 | (1.3) |
где, Qв – расход воды, закачиваемой в данную скважину или приемистость скважины, м 3 /сут.
Коэффициент гидропроводности пласта:
 | (1.4) |
Коэффициент e — наиболее емкая характеристика продуктивного пласта, определяющая его производительность в скважине.
К и ε связаны между собой:
 | (1.5) |
Коэффициент проводимости или подвижности жидкости (нефти, воды) α,характеризующий подвижность жидкости в пластовых условиях в зависимости от ее динамической вязкости µ и проницаемости пласта k: α = k/ µ.
Определение данного параметра необходимо в случае исследования притока к скважинам нефтей, обладающих структурно-механическими свойствами (аномально- и сверханомально-вязкие нефти).
 | (1.6) |
Коэффициент проницаемости пласта k – важнейшая гидродинамическая характеристика пористой среды – характеризует суммарную площадь сечения поровых каналов, по которым идет процесс фильтрации, на единичной площади фильтрации.
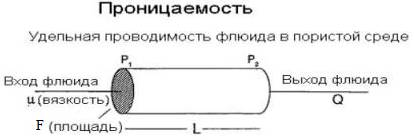
Способы определения коэффициента проницаемости k:
лабораторный — через образец пористой среды длиной l, площадью поперечного сечения F, пропускается жидкость или газ вязкостью μ, с объемным расходом Q, при перепаде давления на входе Р1 и выходе Р2 этого образца ΔP (рис. 1.1). Тогда согласно закона Дарси:
 | (1.7) |
 | (1.8) |
Рис. 1.1. Опыт Дарси по определению проницаемости
Преимущество этого способа — наиболее точный, недостаток — показывает значение k только в точке отбора керна.
o геофизический — определяют при проведении геофизических работ в скважине. Преимущество этого способа — характеризует большую область пласта (осредненно), но только на несколько сантиметров от ствола скважины;
o гидродинамический — позволяет количественно оценить проницаемость призабойной зоны пласта (ПЗП), удаленной зоны пласта и всего пласта в зоне дренирования скважины, но данный способ определения коэффициента проницаемости менее точный, чем лабораторный.
Коэффициент пьезопроводности пласта χ — характеризует способность пласта к передаче возмущений (изменений давления), вызванных изменением режима эксплуатации или характеризует скорость перераспределения давления в пласте в условиях упругого режима. Для однородного пласта применяется формула Щелкачева:
 | (1.9) |
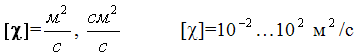 | (1.10) |
где, Βж и Βс — соответственно коэффициент сжимаемости жидкости и пласта;
Β * — коэффициент упругоемкости пласта, Па или см 2 /кгс;
m — эффективная пористость, доли единицы.
Гидродинамическое совершенство скважины характеризуется:
o приведенным радиусом скважины;
o коэффициентом совершенства скважины.
Приведенный радиус скважины — это радиус такой воображаемой скважины (совершенной), которая в аналогичных условиях дает такой же дебит, что реальная скважина (несовершенная).
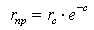 | (1.11) |
Таким образом, приведенный радиус скважины связывает между собой радиус реальной скважины с коэффициентом гидродинамического несовершенства с. Численная величина приведенного радиуса скважины может быть определена по результатам исследования скважины на нестационарном режиме работы скважины.
Коэффициентом гидродинамического совершенства скважины φ называется отношение дебита несовершенной скважины Qнс к дебиту совершенной скважины Qс, и вычисляется по выражению:
 | (1.12) |
В настоящее время гидродинамическое совершенство скважин рассчитывается по результатам экспериментального определения приведенного радиуса rпр, что существенно повышает точность, т.к. отпадает необходимость определения коэффициентов с1 и с2 по специальным графикам Щурова при заведомо неполной и недостоверной информации.
Однако во многих случаях продуктивные пласты вскрываются скважинами не на всю их толщину, а частично, такие скважины считаются несовершенными.
В нефтепромысловой практике совершенных скважин не существует, это теоретическое понятие необходимое для описания работы реальных добывающих скважин и проведения практических расчетов, дебит и другие гидродинамические параметры которых сравнивают с совершенными скважинами. Выделяют три вида несовершенства реальных добывающих скважин (рис. 1.2).
1. Несовершенство по степени вскрытия.
Несовершенство по степени обозначается – с1. Это значит, что скважина вскрывает пласт не на всю мощность (толщину).
2. Несовершенство по характеру вскрытия.
Обозначается – с2. Это означает, что пласт крепится обсадной колонной, которая цементируется, а затем перфорируется.
3. Несовершенство по качеству вскрытия.
Обозначается такой вид несовершенства скважины – S. S – скин-эффект или скин-фактор, явление ухудшения проницаемости в призабойной зоне пласта по разным причинам.
Скин-фактор — гидродинамический параметр, характеризующий дополнительное фильтрационное сопротивление течению флюидов в околоскважинной зоне пласта, приводящее к снижению добычи (дебита) по сравнению с совершенной (идеальной) скважиной. Причинами скин-фактора являются гидродинамическое несовершенство вскрытия пласта, загрязнение околоскважинной зоны, прочие нелинейные эффекты (турбулентное течение, разгазирование, сжатие скелета горной породы и т. д.).
Рис. 1.2. Схемы гидродинамически совершенной (а) и гидродинамически несовершенных скважин:
Скин-фактор и приведённый радиус
По определению скин-фактор описывается формулой:
 | (1.13) |
где, 


После подстановки приведённого радиуса вместо реального радиуса в гидродинамические формулы, описывающие фильтрацию к совершенной скважине, эти формулы становятся пригодными для анализа реальной несовершенной скважины.
Скин-фактор и продуктивность скважины
Применяя уравнение Дюпюи для плоскорадиального установившегося потока несжимаемой жидкости к вертикальной скважине, получаем выражение для скин-фактора:
 | (1.14) |
где, 

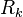

| St = S з + S p + S pp + Sturb + S o + S s + … | (1.15) |
где, Sз – скин-эффект вследствие повреждения породы (+);
Sp – скин-эффект из-за перфорации (+);
Spp – скин-эффект вследствие частичного проникновения скважины в пласт (+);
Sturb – скин-эффект вследствие турбуленции или скин, зависящий от темпа отбора (+);
So – скин-эффект вследствие наклона скважины (-);
Ss – скин-эффект, возникающий вследствие ГРП (-);
Скин-эффект вследствие повреждения породы Sз в лучшем случае может быть изменен до нуля (например – кислотной обработкой). Отрицательный скин возникает вследствие образования трещин (гидроразрыв).
Используя концепцию скина как кольцеобразной зоны вокруг скважины с измененной проницаемостью, Хокинс построил модель скважины, как показано на рис. 1.3. Скин-фактор может быть также вычислен с помощью свойств призабойной зоны.
 | (1.16) |
где, kпл – естественная проницаемость пласта в удаленной зоне, м 2 ;
kз – проницаемость измененной зоны пласта (ПЗС), м 2 ;
rз – радиус измененной зоны пласта (ПЗС), м;
rс – радиус скважины по долоту, м.
Если kз kпл (интенсификация), скин-фактор является отрицательным. Если kз = kпл, (нет повреждения ПЗС по разным причинам или проницаемость ПЗС восстановлена до ее первоначального – естественного состояния), скин-фактор равен 0.
Если величина скин-фактора близка к нулю (практически с учётом погрешности определения: 

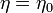
Большая положительная величина скин-фактора 


Рис. 1.3. Модель скин-фактора по Хокинсу
Любое гидродинамическое несовершенство скважины приводит к снижению ее дебита жидкости.
Эффективный радиус скважины
Если проницаемость в зоне изменения kз намного выше, чем проницаемость пласта kпл, то скважина будет вести себя как скважина с вероятным радиусом rэф – эффективный радиус скважины, который может быть вычислен на основе реального радиуса и скин-фактора (рис. 1.4):
 | (1.17 |
 | (1.18 |
Рис. 1.4. Концепция эффективного радиуса скважины
 | (1.19) |
Радиус контура питания (воронки депрессии) – это расстояние от скважины до зоны пласта, где давление полагается постоянным и равным текущему пластовому давлению. Обычно за радиус контура питания скважины в нефтепромысловой практике принимают примерно половину расстояния между двумя добывающими скважинами.
Пример: примем радиус скважины по долоту 108 мм, а радиус дренирования скважины или радиус контура питания – 250 м, при расстоянии между двумя добывающими скважинами – 500 м, тогда:
Анализируя приведенный выше пример с учетом рассмотрения понятия «скин-фактор» или «скин-эффект», можно сказать, что наименьшее фильтрационное сопротивление движению жидкости по пласту к добывающей скважине при всех прочих равных условиях и без ухудшения фильтрационно-емкостных свойств пласта будет на расстоянии от стенки скважины, равном радиусу дренирования или контура питания скважины.
Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим.
Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций.