Изометрия и аксонометрия чем отличаются
Разница между изометрией и аксонометрией
Отображать различные геометрические предметы с помощью чертежей и посредством компьютерной графики можно с применением принципов изометрии и аксонометрии. В чем специфика каждого из них?
Что представляет собой аксонометрия?
Под аксонометрией или аксонометрической проекцией понимается способ графического отображения тех или иных геометрических предметов посредством параллельных проекций.

Геометрический предмет в данном случае чаще всего рисуется с использованием определенной системы координат — так, чтобы та плоскость, на которую он проецируется, не соответствовала положению плоскости других координат соответствующей системы. Получается, что предмет отображается в пространстве посредством 2 проекций и выглядит объемно.
При этом по той причине, что плоскость отображения предмета не расположена строго параллельно какой-либо из осей системы координат, отдельные элементы соответствующего отображения могут искажаться — по одному из 3 следующих принципов.
Во-первых, искажение элементов отображения предметов может наблюдаться по всем 3 осям, используемым в системе, в равной величине. В этом случае фиксируется изометрическая проекция предмета, или изометрия.
Во-вторых, искажение элементов может наблюдаться только по 2 осям в равной величине. В этом случае наблюдается диметрическая проекция.
В-третьих, искажение элементов может фиксироваться как различающееся по всем 3 осям. В этом случае наблюдается триметрическая проекция.
Рассмотрим, таким образом, специфику первого типа искажений, формируемых в рамках аксонометрии.
Что представляет собой изометрия?
Итак, изометрия — это разновидность аксонометрии, которая наблюдается при прорисовке предмета в случае, если искажение его элементов по всем 3 осям координат одинаковое.
Рассматриваемый вид аксонометрической проекции активно применяется в промышленном проектировании. Он позволяет хорошо просматривать те или иные детали в рамках чертежа. Распространено использование изометрии и при разработке компьютерных игр: с помощью соответствующего типа проекции становится возможным эффективно отображать трехмерные картинки.
Можно отметить, что в сфере современных промышленных разработок под изометрией в общем случае понимается прямоугольная проекция. Но иногда она может быть представлена и в косоугольной разновидности.
Сравнение
Главное отличие изометрии от аксонометрии заключается в том, что первый термин соответствует проекции, являющейся только лишь одной из разновидностей той, которая обозначается вторым термином. Изометрическая проекция, таким образом, существенно отличается от других разновидностей аксонометрии — диметрии и триметрии.
Отобразим более наглядно то, в чем разница между изометрией и аксонометрией, в небольшой таблице.
Отличие 3D модели от аксонометрии (изометрии)
Что такое 3D модель
3D-модель – это объемная фигура в пространстве (модель объекта в виде твердого тела), создаваемая в специальной программе: Компас 3D, АutoCAD, Solidworks, и других. По-другому это зрительный объёмный образ желаемого объекта.
3D-модель получается с помощью различных операций (выдавливания, вырезания, вращения и пр.).
После того как модель будет выполнена, на нее можно будет посмотреть с любого ракурса, приблизить, отдалить, внести необходимые корректировки.
Трёхмерная графика активно применяется для создания изображений на плоскости экрана или листа печатной продукции в системах автоматизации проектных работ (САПР; для создания твердотельных элементов: зданий, деталей машин, механизмов).
Трёхмерная графика обычно имеет дело с виртуальным, воображаемым трёхмерным пространством, которое отображается на плоской, двухмерной поверхности дисплея или листа бумаги. В настоящее время известно несколько способов отображения трёхмерной информации в объёмном виде, хотя большинство из них представляет объёмные характеристики весьма условно, поскольку работают со стереоизображением.
Аксонометрия и ее виды
Аксонометрию, в отличие от 3D модели можно выполнить только на плоском чертеже (листе) с помощью программ Компас, АutoCAD, Solidworks, и др., а также на листе бумаги карандашом.
Предмет с системой координат, к которой он отнесён, проецируют на произвольную плоскость (картинная плоскость аксонометрической проекции) таким образом, чтобы эта плоскость не совпадала с его координатной плоскостью. В этом случае получаются две взаимосвязанные проекции одной фигуры на одну плоскость, что позволяет восстановить положение в пространстве, получив наглядное изображение предмета. Так как картинная плоскость не параллельна ни одной из координатных осей, то имеются искажения отрезков по длине параллельных координатным осям. Это искажение может быть равным по всем трём осям — изометрическая проекция, одинаковыми по двум осям — диметрическая проекция и с искажениями разными по всем трём осям — триметрическая проекция.
Геометрическое тело представляет собой совокупность точек. Умея строить модели одной точки, можно получить модели и их совокупности. На рисунке ниже изображена шестигранная призма в ортогональных проекциях и аксонометрии (прямоугольная изометрия). Третья проекция построена с использованием циркуля. Вертикальная прямая проводится на любом расстоянии от заданных проекций.
Для построения аксонометрии на горизонтальной проекции задают оси координат х, у. Сначала строят аксонометрию фигуры основания. Затем из каждой вершины поднимают вертикали и на них откладывают высоту рёбер призмы. Достраивают верхнее основание и обводят ребра с учетом их видимости.
Отличия 3D модели и аксонометрической проекции
Просьба
Учитываю все особенности и отличия 3D-модели от аксонометрической проекции, убедительная просьба не путать эти два разных понятия.
Разница между изометрией и аксонометрией
Отображать различные геометрические предметы с помощью чертежей и посредством компьютерной графики можно с применением принципов изометрии и аксонометрии. В чем специфика каждого из них?
Что представляет собой аксонометрия?
Под аксонометрией или аксонометрической проекцией понимается способ графического отображения тех или иных геометрических предметов посредством параллельных проекций.

Геометрический предмет в данном случае чаще всего рисуется с использованием определенной системы координат — так, чтобы та плоскость, на которую он проецируется, не соответствовала положению плоскости других координат соответствующей системы. Получается, что предмет отображается в пространстве посредством 2 проекций и выглядит объемно.
При этом по той причине, что плоскость отображения предмета не расположена строго параллельно какой-либо из осей системы координат, отдельные элементы соответствующего отображения могут искажаться — по одному из 3 следующих принципов.
Во-первых, искажение элементов отображения предметов может наблюдаться по всем 3 осям, используемым в системе, в равной величине. В этом случае фиксируется изометрическая проекция предмета, или изометрия.
Во-вторых, искажение элементов может наблюдаться только по 2 осям в равной величине. В этом случае наблюдается диметрическая проекция.
В-третьих, искажение элементов может фиксироваться как различающееся по всем 3 осям. В этом случае наблюдается триметрическая проекция.
Рассмотрим, таким образом, специфику первого типа искажений, формируемых в рамках аксонометрии.
Что представляет собой изометрия?
Итак, изометрия — это разновидность аксонометрии, которая наблюдается при прорисовке предмета в случае, если искажение его элементов по всем 3 осям координат одинаковое.

Рассматриваемый вид аксонометрической проекции активно применяется в промышленном проектировании. Он позволяет хорошо просматривать те или иные детали в рамках чертежа. Распространено использование изометрии и при разработке компьютерных игр: с помощью соответствующего типа проекции становится возможным эффективно отображать трехмерные картинки.
Можно отметить, что в сфере современных промышленных разработок под изометрией в общем случае понимается прямоугольная проекция. Но иногда она может быть представлена и в косоугольной разновидности.
Сравнение
Главное отличие изометрии от аксонометрии заключается в том, что первый термин соответствует проекции, являющейся только лишь одной из разновидностей той, которая обозначается вторым термином. Изометрическая проекция, таким образом, существенно отличается от других разновидностей аксонометрии — диметрии и триметрии.
Отобразим более наглядно то, в чем разница между изометрией и аксонометрией, в небольшой таблице.
Таблица
| Изометрия | Аксонометрия |
| Что общего между ними? | |
| Изометрия — разновидность аксонометрии, способ графического отображения предметов с помощью параллельных проекций | |
| В чем разница между ними? | |
| Характеризуется равенством искаженных элементов проекции по всем 3 осям используемой системы координат | Может быть представлена также диметрией (равенством искажений по 2 осям), триметрией (отсутствием равенства искажений при их сопоставлении по 3 осям) |
Аксонометрические проекции
По вопросам репетиторства по инженерной графике (черчению), вы можете связаться любым удобным для вас способом в разделе Контакты. Возможно очное и дистанционное обучение по Skype: 1000 р./ак.ч.
Во многих случаях при выполнении технических чертежей оказывается полезным наряду изображением предметов в системе ортогональных проекций иметь более наглядные изображения. Для построения таких изображений применяются проекции, называемые аксонометрическими.
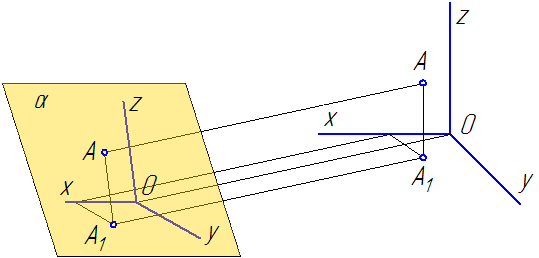
Способ аксонометрического проецирования состоит в том, что данный предмет вместе с осями прямоугольных координат, к которым эта система относится в пространстве, параллельно проецируется на некоторую плоскость α (Рисунок 4.1).
Направление проецирования S определяет положение аксонометрических осей на плоскости проекций α, а также коэффициенты искажения по ним. При этом необходимо обеспечить наглядность изображения и возможность производить определения положений и размеров предмета.
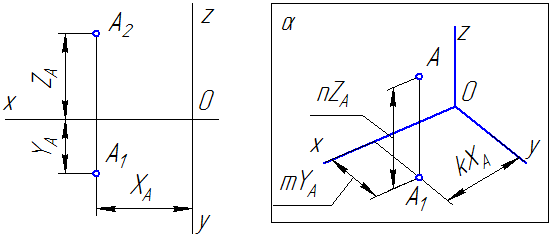
В качестве примера на Рисунке 4.2 показано построение аксонометрической проекции точки А по ее ортогональным проекциям.
Здесь буквами k, m, n обозначены коэффициенты искажения по осям OX, OY и OZ соответственно. Если все три коэффициента равны между собой, то аксонометрическая проекция называется изометрической, если равны между собой только два коэффициента, то проекция называется диметрической, если же k≠m≠n, то проекция называется триметрической.
Если направление проецирования S перпендикулярно плоскости проекций α, то аксонометрическая проекция носит названия прямоугольной. В противном случае, аксонометрическая проекция называется косоугольной.
ГОСТ 2.317-2011 устанавливает следующие прямоугольные и косоугольные аксонометрические проекции:
Ниже приводятся параметры только трех наиболее часто применяемых на практике аксонометрических проекций.
Каждая такая проекция определяется положением осей, коэффициентами искажения по ним, размерами и направлениями осей эллипсов, расположенных в плоскостях, параллельных координатным плоскостям. Для упрощения геометрических построений коэффициенты искажения по осям, как правило, округляются.
4.1. Прямоугольные проекции
4.1.1. Изометрическая проекция
Направление аксонометрических осей приведено на Рисунке 4.3.
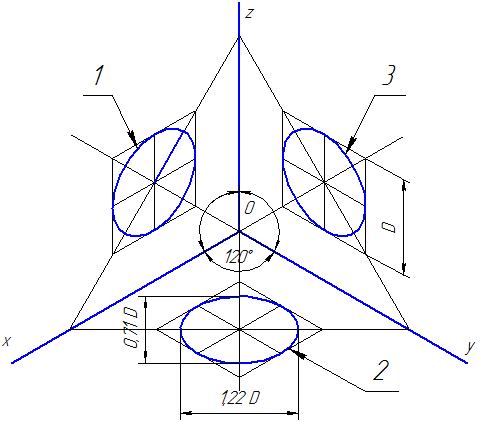
Рисунок 4.3 — Аксонометрические оси в прямоугольной изометрической проекции
Действительные коэффициенты искажения по осям OX, OY и OZ равны 0,82. Но с такими значениями коэффициентов искажения работать не удобно, поэтому, на практике, используются приведенные коэффициенты искажений. Эта проекция обычно выполняется без искажения, поэтому, приведенные коэффициенты искажений принимается k = m = n =1. Окружности, лежащие в плоскостях, параллельных плоскостям проекций, проецируются в эллипсы, большая ось которых равна 1,22, а малая — 0,71 диаметра образующей окружности D.
Большие оси эллипсов 1, 2 и 3 расположены под углом 90º к осям OY, OZ и OX, соответственно.
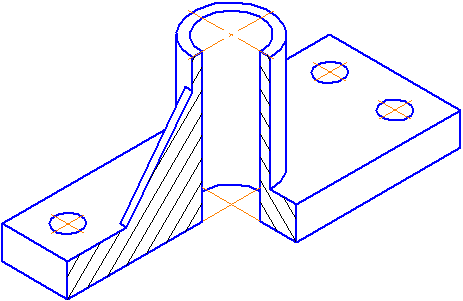
Пример выполнения изометрической проекции условной детали с вырезом приводится на Рисунке 4.4.
Рисунок 4.4 — Изображение детали в прямоугольной изометрической проекции
4.1.2. Диметрическая проекция
Положение аксонометрических осей проводится на Рисунке 4.5.
Для построения угла, приблизительно равного 7º10´, строится прямоугольный треугольник, катеты которого составляют одну и восемь единиц длины; для построения угла, приблизительно равного 41º25´ — катеты треугольника, соответственно, равны семи и восьми единицам длины.
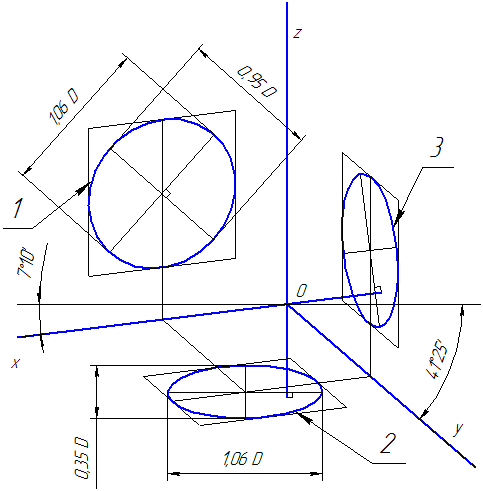
Коэффициенты искажения по осям ОХ и OZ k=n=0,94 а по оси OY — m=0,47. При округлении этих параметров принимается k=n=1 и m=0,5. В этом случае размеры осей эллипсов будут: большая ось эллипса 1 равна 0,95D и эллипсов 2 и 3 — 0,35D (D — диаметр окружности). На Рисунке 4.5 большие оси эллипсов 1, 2 и 3 расположены под углом 90º к осям OY, OZ и OX, соответственно.
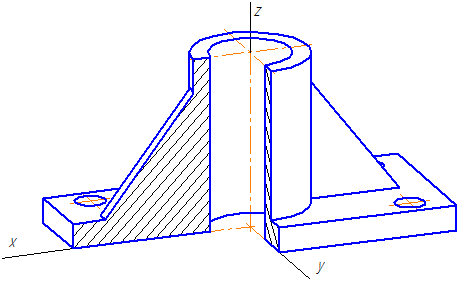
Пример прямоугольной диметрической проекции условной детали с вырезом приводится на Рисунке 4.6.
Рисунок 4.5 — Аксонометрические оси в прямоугольной диметрической проекции
Рисунок 4.6 — Изображение детали в прямоугольной диметрической проекции
4.2 Косоугольные проекции
4.2.1 Фронтальная диметрическая проекция
Положение аксонометрических осей приведено на Рисунке 4.7. Допускается применять фронтальные диметрические проекции с углом наклона к оси OY, равным 300 и 600.
Коэффициент искажения по оси OY равен m=0,5 а по осям OX и OZ — k=n=1.
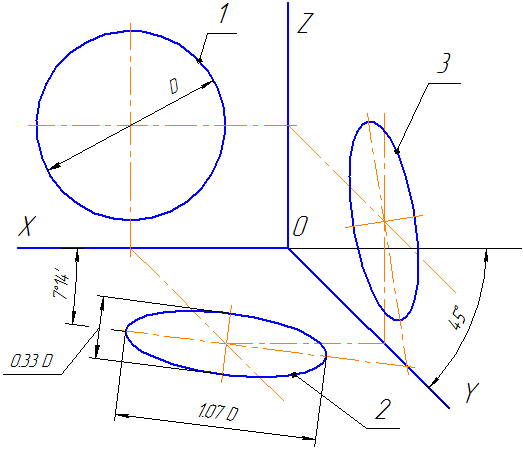
Рисунок 4.7 — Аксонометрические оси в косоугольной фронтальной диметрической проекции
Окружности, лежащие в плоскостях, параллельных фронтальной плоскости проекций, проецируются на плоскость XOZ без искажения. Большие оси эллипсов 2 и 3 равны 1,07D, а малая ось — 0,33D (D — диаметр окружности). Большая ось эллипса 2 составляет с осью ОХ угол 7º 14´, а большая ось эллипса 3 составляет такой же угол с осью OZ.
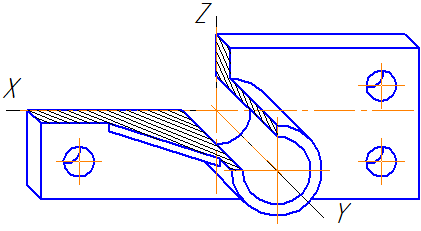
Пример аксонометрической проекции условной детали с вырезом приводится на Рисунке 4.8.
Как видно из рисунка, данная деталь располагается таким образом, чтобы её окружности проецировались на плоскость XОZ без искажения.
Рисунок 4.8 — Изображение детали в косоугольной фронтальной диметрической проекции
4.3 Построение эллипса
4.3.1 Построения эллипса по двум осям
На данных осях эллипса АВ и СD строятся как на диаметрах две концентрические окружности (Рисунок 4.9, а).
Одна из этих окружностей делится на несколько равных (или неравных) частей.
Через точки деления и центр эллипса проводятся радиусы, которые делят также вторую окружность. Затем через точки деления большой окружности проводятся прямые, параллельные линии АВ.
Точки пересечения соответствующих прямых и будут точками, принадлежащими эллипсу. На Рисунке 4.9, а показана лишь одна искомая точка 1.
Рисунок 4.9 — Построение эллипса по двум осям (а), по хордам (б)
4.3.2 Построение эллипса по хордам
Диаметр окружности АВ делится на несколько равных частей, на рисунке 4.9,б их 4. Через точки 1-3 проводятся хорды параллельно диаметру CD. В любой аксонометрической проекции (например, в косоугольной диметрической) изображаются эти же диаметры с учетом коэффициента искажения. Так на Рисунке 4.9,б А1В1=АВ и С1 D1 = 0,5CD. Диаметр А 1В1 делится на то же число равных частей, что и диаметр АВ, через полученные точки 1-3 проводятся отрезки, равные соответственным хордам, умноженным на коэффициент искажение (в нашем случае — 0,5).
4.4 Штриховка сечений
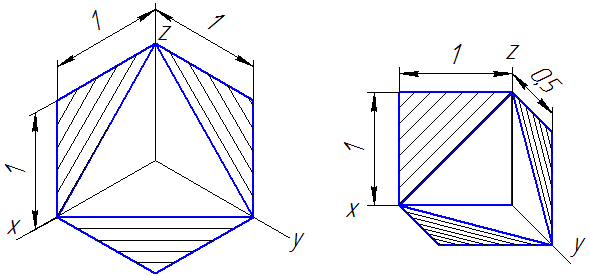
Линии штриховки сечений (разрезов) в аксонометрических проекциях наносятся параллельно одной из диагоналей квадратов, лежащих в соответствующих координатных плоскостях, стороны которых параллельны аксонометрическим осям (Рисунок 4.10: а — штриховка в прямоугольной изометрии; б — штриховка в косоугольной фронтальной диметрии).
Рисунок 4.10 — Примеры штриховки в аксонометрических проекциях
По вопросам репетиторства по инженерной графике (черчению), вы можете связаться любым удобным для вас способом в разделе Контакты. Возможно очное и дистанционное обучение по Skype: 1000 р./ак.ч.
Понятие об аксонометрических проекциях
Наглядные изображения применяют для пояснения чертежей деталей и машин. По ним легче представить форму предмета, чем по чертежу в трёх видах.
Одним из видов наглядных изображений являются аксонометрические изображения.
Аксонометрия в переводе с греческого означает «измерение по осям».
Аксонометрические проекции получают путём проецирования параллельными лучами
предмета, который связан с осями прямоугольных координат, на некоторую плоскость Р (рис. 103).

Таким образом, аксонометрическая проекция — это проекция только на одну плоскость.
Чтобы изображение получилось наглядным, проецирующие лучи не должны быть параллельны ни одной оси координат. Тогда на плоскости Р будут, хоть и с искажениями, изображены все три измерения предмета.
Аксонометрические проекции в зависимости от направления проецирования делятся на два вида: прямоугольные, когда направление проецирования перпендикулярно плоскости Р (угол φ=90°), и косоугольные, когда угол φ≠90°.
Если плоскость Р не параллельна ни одной из координатных плоскостей x,y,z, то на аксонометрической проекции у предмета искажаются все три его измерения. Если же плоскость Р параллельна одной или двум осям координат, то у предмета искажаются размеры соответственно по двум его измерениям или по одному.
Величина искажения определяется коэффициентом искажения, который равен отношению длины аксонометрической проекции отрезка, параллельного соответствующей оси координат, к его действительной длине. Любая аксонометрическая проекция имеет три коэффициента искажения по числу осей координат.
В зависимости от того, разные они или одинаковые, аксонометрические проекции делят на изометрические (коэффициенты искажения равны по всем трём осям) и триметрические (коэффициенты искажения по всем осям разные).
Стандартные виды аксонометрии. Изометрия. Диметрия
Наиболее распространёнными видами аксонометрических проекций являются прямоугольная изометрическая проекция (изометрия) и прямоугольная диметрическая проекция (диметрия), основные правила построения которых определены стандартом.
Прямоугольная изометрия представляет собой аксонометрическую проекцию с направлением проецирования, перпендикулярным к плоскости аксонометрических проекций одинаковыми по всем трём осям коэффициентами искажения, равными 0,82.
Оси изометрии (рис. 104а) составляют между собой углы 120°. Ось Z расположена вертикально. Для упрощения построения коэффициент искажения принимают равным 1.
Изображение при этом получается увеличенным, но вид его не меняется, т.к. сохраняется пропорциональность всех его размеров.
На рис. 104б и в приведены два способа построения осей в изометрии.

Прямоугольная диметрия представляет собой аксонометрическую проекцию с направлением проецирования, перпендикулярным аксонометрической плоскости проекций Р и одинаковыми коэффициентами искажения по осям х и z.
Ось х (рис. 105а) составляет с горизонтальной прямой угол 7°10′, а ось у — угол 41°25′.
Ось z занимает вертикальное положение. На рис. 105б показан графический способ построения осей диметрии.

В диметрии коэффициенты искажения по осям х и z равны 0,94, а по оси у — 0,47. При построениях первый коэффициент округляют до 1, а второй — до 0,5. Таким образом, отрезки, параллельные осям координат х и z, откладывают в натуральную величину, а длину отрезков, параллельных оси у, уменьшают в два раза.
Построение окружности в аксонометрии
Изометрия. Изометрические проекции окружностей, расположенных в плоскостях проекций или в плоскостях, им параллельных, есть эллипсы (рис. 106).

Большие оси этих эллипсов равны l,22Dокр, а малые 0,71Dокр, где Dокр — диаметр изображаемой окружности. Большая ось эллипсов всегда перпендикулярна к той аксонометрической оси, которая отсутствует в плоскости окружности, а малая совпадает с этой осью или параллельна ей.
Практически при построении изометрии окружности эллипс обычно заменяют близким к нему по форме овалом, т.к. построение овала значительно проще.
Наиболее простой способ построения овала показан на рис. 107.

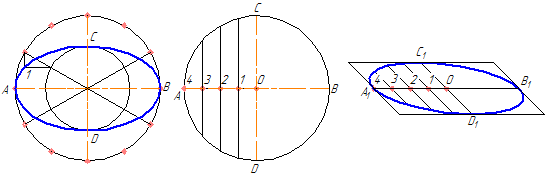
На рис. 108а,б построены изометрии окружностей, расположенных во фронтальной и профильной плоскостях.

Окружности, расположенные во фронтальной плоскости, проецируются в виде эллипсов с большой осью, равной 1,06Dокр, а малой — 0,94Dокр. Большие оси эллипсов, как и в изометрии, перпендикулярны к той аксонометрической оси, которая отсутствует в данной плоскости, а малые оси совпадают с направлением этой оси.

Диметрии окружностей (эллипсы) обычно заменяют овалами, размеры осей которых равны размерам соответствующих осей эллипсов. Построение этих овалов показано на рис. 110. На рис. 110а построения понятны по чертежу.
На рис. 110б строим оси диметрии хр, ур, zр. Затем строим прямую, перпендикулярную оси ур. Отложив на осях хр и zр радиус заданной окружности, получим точки М, К, N, L, которые являются точками сопряжения дуг овала. Через точки М и N проводим горизонтальные прямые. В пересечении этих прямых с осью ур и перпендикуляром к ней получим точки О1, О2, О3, О4. Из центров O1 и О3 опишем дуги радиусом R1=О3 K, а из центров О2 и О4 — дуги радиусом R2=О2M.

Аксонометрические изображения предметов
Приступая к построению аксонометрической проекции предмета, следует выбрать вид аксонометрии, обеспечивающий наибольшую наглядность изображения. Затем предмет связывают с системой прямоугольных координат, оси которой обычно совмещают с осями симметрии предмета. Только после этого можно приступить к построению аксонометрии.
Построение аксонометрии предмета обычно начинают с построения аксонометрии одной из его проекций (вторичной проекции). Затем полученное изображение дополняют построением третьего измерения всех его точек.
На рис. 111 показан пример построения прямоугольной изометрии предмета через построение его горизонтальной проекции.
На рис. 112 приведен пример построения прямоугольной изометрии детали путём построения её вторичной фронтальной проекции.
Для выявления внутренней формы предмета, изображённого в аксонометрии, в некоторых случаях применяют разрезы, которые условно называют вырезами. При этом используют две секущие плоскости, обычно совпадающие с плоскостями симметрии предмета (рис. 113).



Линии штриховки сечений в аксонометрических проекциях наносят параллельно одной из диагоналей проекций квадратов, лежащих в соответствующих координатных плоскостях. Стороны квадратов параллельны аксонометрическим осям (рис. 114).

Что такое 3D модель
3D-модель — это объемная фигура в пространстве (модель объекта в виде твердого тела), создаваемая в специальной программе: Компас 3D, АutoCAD, Solidworks, и других. По-другому это зрительный объёмный образ желаемого объекта.
3D-модель получается с помощью различных операций (выдавливания, вырезания, вращения и пр.).
После того как модель будет выполнена, на нее можно будет посмотреть с любого ракурса, приблизить, отдалить, внести необходимые корректировки.
Трёхмерная графика активно применяется для создания изображений на плоскости экрана или листа печатной продукции в системах автоматизации проектных работ (САПР; для создания твердотельных элементов: зданий, деталей машин, механизмов).
Трёхмерная графика обычно имеет дело с виртуальным, воображаемым трёхмерным пространством, которое отображается на плоской, двухмерной поверхности дисплея или листа бумаги. В настоящее время известно несколько способов отображения трёхмерной информации в объёмном виде, хотя большинство из них представляет объёмные характеристики весьма условно, поскольку работают со стереоизображением.
Аксонометрия и ее виды
Аксонометрия (от др.-греч. ἄξων «ось» + μετρέω «измеряю») — это способ наглядного пространственного (трехмерного) изображения предмета на плоскости (на чертеже) с фиксированным искажением размеров в каждом из трех направлений, по трем координатным осям. В результате на чертеже видны 3 стороны предмета.
Аксонометрию, в отличие от 3D модели можно выполнить только на плоском чертеже (листе) с помощью программ Компас, АutoCAD, Solidworks, и др., а также на листе бумаги карандашом.
Предмет с системой координат, к которой он отнесён, проецируют на произвольную плоскость (картинная плоскость аксонометрической проекции) таким образом, чтобы эта плоскость не совпадала с его координатной плоскостью. В этом случае получаются две взаимосвязанные проекции одной фигуры на одну плоскость, что позволяет восстановить положение в пространстве, получив наглядное изображение предмета. Так как картинная плоскость не параллельна ни одной из координатных осей, то имеются искажения отрезков по длине параллельных координатным осям. Это искажение может быть равным по всем трём осям — изометрическая проекция, одинаковыми по двум осям — диметрическая проекция и с искажениями разными по всем трём осям — триметрическая проекция.
Геометрическое тело представляет собой совокупность точек. Умея строить модели одной точки, можно получить модели и их совокупности. На рисунке ниже изображена шестигранная призма в ортогональных проекциях и аксонометрии (прямоугольная изометрия). Третья проекция построена с использованием циркуля. Вертикальная прямая проводится на любом расстоянии от заданных проекций.
Для построения аксонометрии на горизонтальной проекции задают оси координат х, у. Сначала строят аксонометрию фигуры основания. Затем из каждой вершины поднимают вертикали и на них откладывают высоту рёбер призмы. Достраивают верхнее основание и обводят ребра с учетом их видимости.
Отличия 3D модели и аксонометрической проекции
Просьба
Учитываю все особенности и отличия 3D-модели от аксонометрической проекции, убедительная просьба не путать эти два разных понятия.