Известно что а множество спортсменов класса в множество отличников класса

Решение задач с помощью «Кругов Эйлера»

РЕШЕНИЕ ЗАДАЧ С ПОМОЩЬЮ «КРУГОВ ЭЙЛЕРА»

«… круги очень подходят для того, чтобы облегчить наши размышления»

Нет ученого, имя которого упоминалось бы в учебной математической литературе столь же часто, как имя Эйлера. Даже в средней школе логарифмы и тригонометрию изучают до сих пор в значительной степени «по Эйлеру».

В 1741 году Эйлер пишет «Письма о разных физических и философических материях, написанные к некоторой немецкой принцессе. », где появились впервые «круги Эйлера». Эйлер писал тогда, что «круги очень подходят для того, чтобы облегчить наши размышления».

При решении целого ряда задач Леонард Эйлер использовал идею изображения множеств с помощью кругов и они получили название «круги Эйлера».

С помощью этих кругов Эйлер изобразил и множество всех действительных чисел:

· N — множество натуральных чисел,

· Z — множество целых чисел,

· Q — множество рациональных чисел,

· R — множество всех действительных чисел.

Рисунок 1. Изображение множества действительных чисел

Что такое множество?

В математике нет точного определения этого понятия. Понятие «множество» не определяется, оно поясняется примерами: множество яблок в корзине; множество точек отрезка прямой. Множество состоит из элементов. В приведенных примерах — это яблоки, буквы, точки.

Под множеством можно понимать совокупность каких-либо объектов, называемых элементами множества [1, с. 18]. Примерами множеств могут быть и дома на нашей улице, и алфавит — совокупность букв, и наш 5 «Д» класс — множество учеников.

Множества могут быть:

· Конечное (элементы которого можно пересчитать; например — множество цифр)

· Бесконечное (пересчитать нельзя; например — песчинки в пустыне)

· Пустое (не содержащее ни одного элемента; например — множество зайцев, которые учатся в нашем классе).

Множество K называется подмножеством множества N, если каждый элемент множества K является элементом множества N. Обозначается: KНN. Говорят, что множество K включается в множество N.

Подмножества можно проиллюстрировать кругами Эйлера.

Рисунок 2. Изображение подмножества

Действия с множествами

В математике существуют несколько операций над множествами. Мы разберем два из них: пересечение и объединение.

1. Пересечение множеств

Пересечением множеств M и N называется множество, состоящее из элементов, одновременно принадлежащих M и N. Пересечение множеств M и N обозначается [1, с. 23].

Пример. Множество N = < А Н Д Р Е Й >;

множество K = < А Л Е К С Е Й >; множество M =

Рисунок 3. Пример пересечения множеств

2. Объединение множеств

Объединение множеств — это множество, содержащее в себе все элементы исходных множеств. Объединение множеств M и N обозначается .

Пример ; 2) объединение множества всех пород собак и множества мопсов есть множество всех собак.

Операции объединения и пересечения множеств очень удобно показывать с помощью кругов Эйлера.

По определению в пересечение двух множеств M и N входят элементы, принадлежащие множествам M и N одновременно

Пример. Пусть D — множество из 12 самых хороших девочек, M — множество из 12 самых умных мальчиков. Получили наш класс.

Рисунок 4. Пример объединения множеств

3. Вложенные множества.

Пример. Имеется три множества: «дети», «школьники», «учащиеся начальной школы». Мы видим, что эти 3 множества находятся одно внутри другого. Про множество, находящееся внутри другого множества, говорят, что оно вложенное.

Рисунок 5. Пример вложенных множеств

Задачи, которые можно решить с помощью диаграмм Эйлера

На стол бросили две салфетки 10 см х 10 см. Они покрыли площадь стола, равную 168. Какова площадь перекрытия?

Рисунок 6. Рисунок к задаче № 1

В поход ходили 80 % учеников класса, а на экскурсии было 60 %, причем каждый был в походе или на экскурсии. Сколько процентов класса были и там, и там?

А — множество учеников, которые ходили в поход

В — множество учеников, которые были на экскурсии

Рисунок 7. Рисунок к задаче № 2

В нашем классе 24 ученика. Все они хорошо провели зимние каникулы.10 человек катались на лыжах, 16 ездили на каток, а 12 — лепили снеговиков. Сколько учеников смогли покататься и на лыжах, и на коньках, и слепить снеговика?

А — множество ребят, катающихся на лыжах

В — множество ребят, катающихся на коньках

С — множество ребят, лепивших снеговиков

Пусть х — число ребят,

которые успели за эти каникулы всё!

Рисунок 8. Рисунок к задаче № 3

9 моих друзей любят бананы, 8 – апельсины, а 7 – сливы, 5 – бананы и апельсины, 3 – бананы и сливы, 4 – апельсины и сливы, 2 – бананы, апельсины и сливы. Сколько у меня друзей?

5 – 2 = 3 3 – 2 = 1 4 – 2 = 2

9 – 6 = 3 8 – 7 = 1 7 – 5 = 2

3 + 1 + 2 + 3 + 2 + 1 + 2 = 14

Рисунок 9. Рисунок к задаче № 4

В пионерском лагере «Дубки» в смене актива отдыхали: 30 отличников, 28 победителей олимпиад и 42 спортсмена. 10 человек были и отличниками и победителями олимпиад, 5 — отличниками и спортсменами, 8 — спортсменами и победителями олимпиад, 3 — и отличники, и спортсмены, и победители олимпиад.

Сколько ребят отдыхали в лагере?

А — множество отличников

В — множество победителей олимпиад

С — множество спортсменов

10 – 3 = 7 5 – 3 = 2 8 – 3 = 5

30 – 12 = 18 28 – 15 = 13 42 – 10 = 32

18 + 13 + 32 + 7 + 2 + 5 + 3 = 80

Рисунок 10. Рисунок к задаче № 5

Диаграммы Эйлера — это общее название целого ряда способов графической иллюстрации, широко используемых в различных областях математики: теория множеств, теория вероятностей, логика, статистика, компьютерные науки, и др. Применение кругов Эйлера позволяет даже пятикласснику легко решать задачи, которые обычным путем решаются только в старших классах.

1., Элементы теории множеств и математической логики. Практикум / Калининград. 1997. — 66 с.

2., За страницами учебника математики. Пособие для учащихся 5—6 кл. М.: Просвещение, 1999. с. 189—191, 231.

5. Дополнительные главы по математике для учащихся 5 класса. СПб: СМИО Пресс, 2009. — с. 14—20.

Сколько ребят увлекаются одновременно тремя видами спорта?

Сколько ребят увлекается лишь одним из этих видов спорта?

оспользуемся кругами Эйлера.

Пусть большой круг изображает всех учащихся класса,

а три меньших круга Б, Х и Ф изображают соответственно баскетболистов, хоккеистов и футболистов.

Тогда фигура Z, общая часть кругов Б, Х и Ф, изображает ребят, увлекающихся тремя видами спорта.

одним лишь хоккеем

одним лишь футболом

Составляем уравнение, пользуясь тем, что класс разбился на отдельные группы ребят; количества ребят в каждой группе обведены на рисунке рамочкам:

Таким образом, двое ребят увлекаются всеми тремя видами спорта.

Двое ребят увлекаются всеми тремя видами спорта человека.

Увлекающихся лишь одним видом спорта: 21 человек.

Круги Эйлера – задачи на пересечение или объединение множеств

Это новый тип задач, в которых требуется найти некоторое пересечение множеств или их объединение, соблюдая условия задачи.

Круги Эйлера — геометрическая схема, с помощью которой можно изобразить отношения между подмножествами, для наглядного представления.

Метод Эйлера является незаменимым при решении некоторых задач, а также упрощает рассуждения. Однако, прежде чем приступить к решению задачи, нужно проанализировать условие. Иногда с помощью арифметических действий решить задачу легче.

“Обитаемый остров” и “Стиляги”

Некоторые ребята из нашего класса любят ходить в кино. Известно, что 15 ребят смотрели фильм «Обитаемый остров», 11 человек – фильм «Стиляги», из них 6 смотрели и «Обитаемый остров», и «Стиляги». Сколько человек смотрели только фильм «Стиляги»?

Чертим два множества таким образом:

6 человек, которые смотрели фильмы «Обитаемый остров» и «Стиляги», помещаем в пересечение множеств.

15 – 6 = 9 – человек, которые смотрели только «Обитаемый остров».

11 – 6 = 5 – человек, которые смотрели только «Стиляги».

Ответ. 5 человек смотрели только «Стиляги».

Среди школьников шестого класса проводилось анкетирование по любимым мультфильмам. Самыми популярными оказались три мультфильма: «Белоснежка и семь гномов», «Губка Боб Квадратные Штаны», «Волк и теленок». Всего в классе 38 человек. «Белоснежку и семь гномов» выбрали 21 ученик, среди которых трое назвали еще «Волк и теленок», шестеро – «Губка Боб Квадратные Штаны», а один написал все три мультфильма. Мультфильм «Волк и теленок» назвали 13 ребят, среди которых пятеро выбрали сразу два мультфильма. Сколько человек выбрали мультфильм «Губка Боб Квадратные Штаны»?

В этой задаче 3 множества, из условий задачи видно, что все они пересекаются между собой. Получаем такой чертеж:

Учитывая условие, что среди ребят, которые назвали мультфильм «Волк и теленок» пятеро выбрали сразу два мультфильма, получаем:

21 – 3 – 6 – 1 = 11 – ребят выбрали только «Белоснежку и семь гномов».

13 – 3 – 1 – 2 = 7 – ребят смотрят только «Волк и теленок».

38 – (11 + 3 + 1 + 6 + 2 + 7) = 8 – человек смотрят только «Губка Боб Квадратные Штаны».

Делаем вывод, что «Губка Боб Квадратные Штаны» выбрали 8 + 2 + 1 + 6 = 17 человек.

Ответ. 17 человек выбрали мультфильм «Губка Боб Квадратные Штаны».

В магазин «Мир музыки» пришло 35 покупателей. Из них 20 человек купили новый диск певицы Максим, 11 – диск Земфиры, 10 человек не купили ни одного диска. Сколько человек купили диски и Максим, и Земфиры?

Изобразим эти множества на кругах Эйлера.

Теперь посчитаем: Всего внутри большого круга 35 покупателей, внутри двух меньших 35–10=25 покупателей. По условию задачи 20 покупателей купили новый диск певицы Максим, следовательно, 25 – 20 = 5 покупателей купили только диск Земфиры. А в задаче сказано, что 11 покупателей купили диск Земфиры, значит 11 – 5 = 6 покупателей купили диски и Максим, и Земфиры:

Ответ: 6 покупателей купили диски и Максим, и Земфиры.

Гарри Поттер, Рон и Гермиона

На полке стояло 26 волшебных книг по заклинаниям. Из них 4 прочитал и Гарри Поттер, и Рон. Гермиона прочитала 7 книг, которых не читали ни Гарри Поттер, ни Рон, и две книги, которые читал Гарри Поттер. прочитал 11 книг. Сколько книг прочитал Рон?

Учитывая условия задачи, чертеж будет таков:

Так как Гарри Поттер всего прочитал 11 книг, из них 4 книги читал Рон и 2 книги – Гермиона, то 11 – 4 – 2 = 5 – книг прочитал только Гарри. Следовательно,

26 – 7 – 2 – 5 – 4 = 8 – книг прочитал Рон.

Ответ. 8 книг прочитал Рон.

В пионерском лагере 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют, не увлекаются спортом, не занимаются в драмкружке? Сколько ребят заняты только спортом?

Изобразим множества следующим образом:

70 – (6 + 8 + 10 + 3 + 13 + 6 + 5) = 19 – ребят не поют, не увлекаются спортом, не занимаются в драмкружке. Только спортом заняты 5 человек.

Ответ. 5 человек заняты только спортом.

Из 100 ребят, отправляющихся в детский оздоровительный лагерь, кататься на сноуборде умеют 30 ребят, на скейтборде – 28, на роликах – 42. На скейтборде и на сноуборде умеют кататься 8 ребят, на скейтборде и на роликах – 10, на сноуборде и на роликах – 5, а на всех трех – 3. Сколько ребят не умеют кататься ни на сноуборде, ни на скейтборде, ни на роликах?

Всеми тремя спортивными снарядами владеют три человека, значит, в общей части кругов вписываем число 3. На скейтборде и на роликах умеют кататься 10 человек, а 3 из них катаются еще и на сноуборде. Следовательно, кататься только на скейтборде и на роликах умеют 10-3=7 ребят. Аналогично получаем, что только на скейтборде и на сноуборде умеют кататься 8-3=5 ребят, а только на сноуборде и на роликах 5-3=2 человека. Внесем эти данные в соответствующие части. Определим теперь, сколько человек умеют кататься только на одном спортивном снаряде. Кататься на сноуборде умеют 30 человек, но 5+3+2=10 из них владеют и другими снарядами, следовательно, только на сноуборде умеют кататься 20 ребят. Аналогично получаем, что только на скейтборде умеют кататься 13 ребят, а только на роликах – 30 ребят. По условию задачи всего 100 ребят. 20+13+30+5+7+2+3=80 – ребят умеют кататься хотя бы на одном спортивном снаряде. Следовательно, 20 человек не умеют кататься ни на одном спортивном снаряде.

Ответ. 20 человек не умеют кататься ни на одном спортивном снаряде.

Задача: В классе учатся 40 человек. Из них по русскому языку имеют «тройки» 19 человек, по математике – 17 человек и по физике – 22 человека. Только по одному предмету имеют «тройки»: по русскому языку – 4 человека, по математике – 4 человека и по физике – 11 человек. Семь человек имеют «тройки» и по математике и по физике, из них пятеро имеют тройки и по русскому языку. Сколько человек учатся без «троек». Сколько человек имеют «тройки» по двум из трёх предметов. Рассмотрим решение с помощью следующего слайда

Теория графов – наука сравнительно молодая. Первая работа по теории графов принадлежит Леонарду Эйлеру. Она появилась в 1736 году в публикациях Петербургской Академии Наук и начиналась с рассмотрения задачи о кенигсбергских мостах. Графы придали условиям наглядность, упростили решение и выявили сходство задач. Сейчас почти в любой отрасли науки и техники встречаешься с графами: в электротехнике при построении электрических схем, в химии – при изучении молекул и их цепочек, в экономике – при решении задач выбора оптимального пути для потоков грузового транспорта. Граф – это фигура, состоящая из точек и линий.

Решим следующую задачу:

В школьном драматическом кружке решили ставить гоголевского «Ревизора». И тут разгорелся жаркий спор. Всё началось с Ляпкина-Тяпкина.

– Ляпкиным-Тяпкиным буду я! Решительно заявил Дима. С раннего детства я мечтал воплотить этот образ на сцене.

– Ну хорошо, согласен уступить эту роль, если мне дадут сыграть Хлестакова, проявил великодушие Гена.

– … А мне – Осипа, – не уступил ему в великодушии Дима.

– Хочу быть Земляникой или Городничим, – сказал Вова.

– Нет, Городничим буду я, – хором закричали Алик и Боря. – или Хлестаковым, добавили они одновременно.

Удастся ли распределить роли так. Чтобы исполнители были довольны?

Изобразим каждого участника драматического кружка точкой, а все их пожелания будем изображать линиями. Видно, что Осипа будет играть Дима, Вова – Землянику, Гена – Ляпкина – Тяпкина, Алик и Боря – Хлестакова и Городничего.

Решите с помощью графов следующую задачу: В первенстве класса по настольному теннису 6 участников: Андрей, Борис, Виктор, Галина, Дмитрий и Елена. Первенство проводят по круговой системе – каждый из участников играет с каждым из остальных один раз.

Всеми тремя языками владеют три туриста, значит, в общей части кругов вписываем число 3. Английским и французским языками владеют 10 человек, а 3 из них владеют еще и немецким. Следовательно, только английским и французским владеют 10-3=7 человек.

Аналогично получаем, что только английским и немецким владеют 8-3=5 человек, а немецким и французским 5-3=2 туриста. Вносим эти данные в соответствующие части.

По условию задачи всего 100 туристов. 20+13+30+5+7+2+3=80 туристов знают хотя бы один язык, следовательно, 20 человек не владеют ни одним из данных языков.

Задачи на круги Эйлера

Задача 1. Про учеников школы, которые участвовали в физико-математическом конкурсе, известно, что 7 из них справились с задачами и по математике и по физике, 11 из них справились с задачами по математике, 9 из них справились с задачами по физике. Сколько учеников принимали участие в конкурсе?

Задача 5. Дано 6 гирь: две зеленых, две красных, две синих. В каждой паре одна гиря тяжелая, а другая легкая, причём все тяжелые гири весят одинаково и все легкие тоже. Можно ли за 2 взвешивания на чашечных весах найти все тяжелые гири?

Задача 6. На плоскости расположено 11 шестерёнок, соединенных в кольцо. Могут ли все шестерёнки вращаться одновременно?

Источник

Загадочные круги Эйлера

Урок 30. Математика и игры 3–4 классы

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока “Загадочные круги Эйлера”

Сегодня на занятии рассмотрим логические задачи, при решении которых удобно применять так называемые круги Эйлера.

Леонард Эйлер был выдающимся учёным. Жил он в XVIII веке. Эйлер внёс огромный вклад в развитие физики, математики, астрономии и других наук. Его именем названы более 20 математических формул. В день 200-летия со дня рождения этого великого математика было издано на его родине, в Швейцарии, всё его наследие, которое состояло из 72 томов по 600 страниц.

Ну а что это за круги Эйлера, вы увидите вот на таком примере.

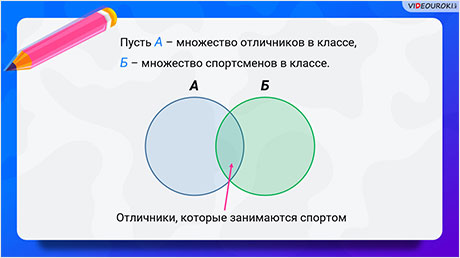
Пусть, например, А – множество отличников в классе, а Б – множество спортсменов в этом же классе.

Нарисуем круг, который изображает множество А. Нарисуем круг, который изображает множество Б. Тогда общая часть этих кругов изображает отличников, которые занимаются спортом.

Отметим, что иногда вместо кругов для изображения множеств применяют фигуры другой формы, например, овалы.

Применение кругов Эйлера при решении некоторых видов задач придаёт им наглядность и простоту.

Давайте решим такую задачу. У всех друзей Миши есть домашние питомцы. 7 друзей любят и держат кошек, а 5 – собак. И только у 3 есть и кошка, и собака. Сколько у Миши друзей?

Решим следующую задачу. 35 шестиклассников являются читателями школьной и районной библиотек. Из них 25 берут книги в школьной библиотеке, 20 – в районной. Сколько учеников не являются читателями районной библиотеки?

Можно узнать, сколько учеников посещают только районную библиотеку.

Следующая задача. Сколько в классе учащихся, если известно, что лыжным спортом увлекаются 28 человек, отличников в классе 12, причём отличников-спортсменов, увлекающихся лыжами, 10 человек?

Отметим, что правильнее будет сказать, что в классе не менее 30 учеников, ведь могут быть ученики, которые не являются ни лыжниками, ни отличниками.

Решим такую задачу. Известно, что из всех учеников класса художественную школу посещают 10 человек. Музыкальную школу – 8 человек. Спортивную школу – 12 человек. Две школы, художественную и музыкальную, – 3. Две школы, музыкальную и спортивную, – 2. Две школы, художественную и спортивную, – 2. Все три школы посещает 1 человек. Сколько учеников посещают только одну школу?

Источник

Практические занятия по дисциплине Математика ЕН.01 для студентов очной формы обучения специальности: 21.02.05 Земельно-имущественные отношения.

Онлайн-конференция

«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»

Свидетельство и скидка на обучение каждому участнику

МИНИСТЕРСТВО ОБРАЗОВАНИЯ СТАВРОПОЛЬСКОГО КРАЯ

Государственное бюджетное образовательное учреждение

«Ставропольский строительный техникум»

для студентов очной формы обучения специальности:

на заседании цикловой комиссии
естественно-математических дисциплин

Председатель цикловой комиссии

______________ / Н.Б. Берлова /

заместитель директора по МРК

Л.В. Печалова, методист
Центра менеджмента качества и методической работы техникума

Н.А. Ваганова, преподаватель математики

Т.В. Рыбина, преподаватель ГБПОУ ССТ
« » 20 г.
___________________

2.Практические занятия…………………. 6

Практическое занятие №2………………………………………….11

Практическое занятие №3………………………………………….18

Практическое занятие №4………………………………………….28

Практическое занятие №5………………………………………….41

В результате изучения дисциплины студент должен:

– значение математики в профессиональной деятельности и при освоении профессиональной образовательной программы;

– основные математические методы решения прикладных задач в области профессиональной деятельности;

– основные понятия и методы математического анализа, дискретной математики, линейной алгебры, теории комплексных чисел, теории вероятностей и математической статистики;

– основы интегрального и дифференциального исчисления.

– решать прикладные задачи в области профессиональной деятельности;

Сборник состоит из пояснительной записки, описания практических занятий, которые снабжены общими теоретическими сведениями, примерами решения типовых заданий, контрольными вопросами и заданиями для самостоятельной работы.

Сборник практических занятий окажет помощь преподавателям в организации занятий, а также может пригодиться студентам при повторении изученного материала и подготовке к дифференцированному зачету.

Цель: закрепить навыки осуществления операций над множествами, навыки использования диаграмм Эйлера-Венна.

При выполнении работы студент должен знать:

понятия множества, подмножества, универсального множества, пересечения множеств, объединения множеств, разности двух множеств и дополнения; понятие диаграмм Эйлера-Венна.

После окончания занятия необходимо уметь:

находить пересечение, объединение, разность и дополнение множеств, в том числе с использованием диаграмм Эйлера-Венна.

ОК 1. Понимать сущность и социальную значимость своей будущей профессии, проявлять к ней

ОК 2. Организовывать собственную деятельность, выбирать типовые методы и способы выполнения профессиональных задач, оценивать их эффективность и качество.

ОК 4. Осуществлять поиск и использование информации, необходимой для эффективного выполнения профессиональных задач, профессионального и личностного развития.

Порядок выполнения работы:

2.Рассмотреть примеры решения типовых заданий.

3. Ответить на контрольные вопросы.

4. Выполнить самостоятельную работу .

5. Сдать отчет по проделанной работе.

Основные теоретические положения и примеры решения типовых заданий.

Понятие множества. Подмножества.

Понятие множества относится к аксиоматическим понятиям математики.

Множество – совокупность определённых, различимых между собой объектов, рассматриваемых как единое целое, и обладающая некоторым общим свойством.

Имеется три важных момента, характеризующих понятие множества:

1) объекты, входящие во множество, определённые – т.е. для каждого объекта можно однозначно сказать, принадлежит ли он данному множеству или нет;

2) объекты, входящие во множество, различимы между собой – т.е. во множестве не может быть двух или более одинаковых объектов;

3) все объекты, входящие во множество, мыслятся как единое целое – т.е. во множестве абстрагируются от свойств отдельных объектов, но говорят об общем свойстве множества, как единого целого; такое общее свойство называют характеристическим.

– множество букв русского алфавита;

– множество натуральных чисел;

– множество студентов, сидящих на 1-м ряду.

– буква «бэ» принадлежит множеству букв русского алфавита;

– буква «бета» не принадлежит множеству букв русского алфавита;

– число 5 принадлежит множеству натуральных чисел;

– число 5,5 – не принадлежит множеству натуральных чисел;

– Вольдемар не сидит в первом ряду.

Таким образом, если множество содержит конечное число элементов, то оно может быть задано перечислением его элементов. Множество может быть также задано при помощи правила, позволяющего определить, является ли данный объект элементом множества или нет. При записи правило, задающее множество, отделяется вертикальной чертой или двоеточием.

Множества А и В считаются равными, если они состоят из одних и тех же элементов. Равенство множеств обозначают так: А = В.

Операции над множествами. Диаграммы Эйлера-Венна.

Пример 3. Пусть А – множество различных букв в слове «математика», а В – множество различных букв в слове «стереометрия». Найти пересечение и объединение множеств А и В.

• объединение А ∪ В • пересечение А∩В • разность А\В • дополнение A

Пример 3. В классе английский язык изучают 25 человек, а немецкий – 27 человек, причем 18 человек изучают одновременно английский и немецкий языки. Сколько человек в классе: а) изучают иностранные языки? б) изучают только английский язык? в) изучают только немецкий язык?

Решение.

Пример 4. Используя диаграммы Эйлера-Венна доказать тождество:

Левая часть равенства представлена на рисунке а), правая – на рисунке б). Из диаграмм очевидно равенство левой и правой частей данного соотношения.

Разбиение множества на классы.

Говорят, что множество Х разбито на попарно непересекающиеся подмножества или классы, если выполнены следующие условия:

1) любые два подмножества попарно не пересекаются;

2) объединение всех подмножеств совпадает с исходным множеством Х.

Классификацию можно выполнять при помощи свойств элементов множества.

Если элементы множества обладают двумя независимыми свойствами, то все множество разбивается на 4 класса.

Пример 5. Пусть Х – множество четырехугольников, А, В и С – его подмножества. Можно ли говорить о разбиении множества Х на классы А, В и С, если:

а) А – множество параллелограммов, В – множество трапеций, С – множество четырехугольников, противоположные стороны которых не параллельны;

б) А – множество параллелограммов, В – множество трапеций, С – множество четырехугольников, имеющих прямой угол?

а) Множества А, В и С попарно не пересекаются. Действительно, если у четырехугольника, противоположные стороны не параллельны, то он не может быть параллелограммом или трапецией. В параллелограмме противоположные стороны попарно параллельны, поэтому он не может принадлежать ни множеству В, ни множеству С. Наконец, в трапеции две противоположные стороны параллельны, а две другие не параллельны, поэтому трапеция не может принадлежать ни множеству А, ни множеству С. Объединение множеств А, В и С даст все множество четырехугольников. Условия классификации выполнены, множество всех четырехугольников можно разбить на параллелограммы, трапеции и четырехугольники, противоположные стороны которых не параллельны.

б) Множества А и В не пересекаются, но множества А и С имеют общие элементы, примером может служить прямоугольник, множества В и С тоже пересекаются: общим элементом является прямоугольная трапеция. Следовательно, нарушено первое условие классификации. Не выполняется и второе условие, так как некоторые четырехугольники не попадают ни в одно из подмножеств А, В или С, таким является четырехугольник с непараллельными сторонами и непрямыми углами. В этом случае множество Х на классы А, В и С не разбивается.

Задания для самостоятельной работы.

Задания выполняются по вариантам, заданным преподавателем.

Задание 1. Образуйте все подмножества множества букв в слове.

Задание 2. Данные множества задать перечислением всех своих элементов.

Задание 4. Используя диаграммы Эйлера-Венна доказать тождество.

Решите задачу используя круги Эйлера: В группе английский язык изучают 15 студентов, немецкий – 10 студентов, а французский – 5, причем 3 студента изучают одновременно английский и немецкий языки, 2 студента изучают одновременно английский и французский языки, 1 студент изучает одновременно французский и немецкий языки. Сколько всего человек в классе изучают эти иностранные языки? Сколько человек изучают только английский язык? немецкий язык? французский язык?

Какое множество называется конечным? пустым?

Что называется пересечением двух множеств?

Что такое диаграмма Эйлера-Венна?

Известно, что А – множество спортсменов группы, В – множество отличников группы. Сформулируйте условия, при которых: а) А∩В=Ø б)АUВ=А.

Время на выполнение: 90- мин. (час.),

выполнение 1 час.10 мин.;

оформление и сдача 10 мин.

Работа выполняется в тетради для практических работ.

Шкала оценки образовательных достижений

Процент результативности (правильных ответов)

Оценка уровня подготовки

Практическая работа №2

Тема: «Вычисление пределов функции»

Цель: Формирование навыков вычисления пределов с помощью замечательных пределов, раскрытия неопределенностей.

. При выполнении практической работы студент должен знать:

-понятие предела функции;

– 1и 2 замечательные пределы;

-понятие непрерывной функции;

После окончания занятия необходимо у меть:

-применять теоремы о приделах;

-применять формулы замечательных пределов;

ОК 2. Организовывать собственную деятельность, выбирать типовые методы и способы

выполнения профессиональных задач, оценивать их эффективность и качество.

ОК 3. Принимать решения в стандартных и нестандартных ситуациях и нести за них

ОК 4. Осуществлять поиск и использование информации, необходимой для эффективного выполнения профессиональных задач, профессионального и личностного развития.

Порядок выполнения работы:

1.Изучить теоретический материал по теме «Пределы».

2.Рассмотреть примеры решения типовых заданий.

3. Ответить на контрольные вопросы.

4. Выполнить самостоятельную работу .

5. Сдать отчет по проделанной работе.

Краткие теоретические сведения

Имеют место основные теоремы, на которых основано вычисление пределов элементарных функций.

Более сложными случаями нахождения предела являются такие, когда подстановка предельного значения аргумента в выражение для приводит к одной из неопределенностей :

Тогда вычисление предела заключается в раскрытии полученных неопределенностей.

Здесь могут оказаться полезными:

Кроме того, при раскрытии неопределенностей используют следующие приемы:

сокращение дроби на критический множитель при ;

избавление от иррациональности в числителе или знаменателе дроби;

Решение: 1) ; выполним преобразования и воспользуемся вторым замечательным пределом.

Примером непрерывной функции может служить любая элементарная функция, которая непрерывна в каждой точке своей области определения.

Точки разрыва функции делятся два типа. К точкам разрыва I рода относятся такие точки, в которых существуют конечные односторонние пределы: (левый предел) и (правый предел). К точкам разрыва II рода относятся те точки, в которых хотя бы один из односторонних пределов не существует или бесконечен.

Задание 1: Вычислите односторонние пределы: 1) ;

Следовательно, при функция имеет бесконечный разрыв; есть точка II рода.

Таким образом, левый и правый пределы исследуемой функции при конечны, но не равны между собой. Поэтому точка I рода, причем точка скачка функции.

Задания для самостоятельной работы

Задание 2.Исследуйте функцию на непрерывность:

Задание 1.Вычислить пределы.

Задание 2.Исследуйте функцию на непрерывность:

Что называется пределом функции?

Сформулируйте основные теоремы вычисления пределов.

Запишите формулы соответствующие первому и второму замечательным пределам.

Какие приемы используются при раскрытии неопределенностей?

5.Дайте определение непрерывной функции.

6.Что называется точкой разрыва?

7.Какая точка называется точкой устранимого разрыва?

8.Какая точка называется точкой скачка? Что называется скачком?

Время на выполнение: 90- мин. (час.),

выполнение 1 час.10 мин.;

оформление и сдача 10 мин.

Работа выполняется в тетради для практических работ.

Шкала оценки образовательных достижений

Процент результативности (правильных ответов)

Оценка уровня подготовки

Практическая работа №3

Тема: « Нахождение дифференциалов функций».

Цель: закрепить навыки нахождения производной и дифференциала.

При выполнении практической работы студент должен знать:

-определение производной, ее геометрический и механический смысл;

правила и формулы дифференцирования функций;

-определение дифференциала функции и его геометрический смысл; определение второй производной, ее физический смысл;

-необходимые и достаточные условия возрастания и убывания функции, существования экстремума;

-общую схему построения графиков функций

определение производной функции;

− теоремы о дифференцировании суммы, произведения, частного, сложной функции;

− геометрический и физический смысл производной функции.

− области практического применения производной функции.

понятие дифференциала функции;

− понятие полного и частного дифференциала;

− формулу приближенных вычислений значений функции в точке с помо-щью дифференциала.

После окончания занятия необходимо у меть:

− вычислять производные функций по определению и таблице производных;

− применять теоремы о производных;

− решать задачи с использованием производных.

-находить дифференциал функции;

− применять формулу приближенных вычислений значения функции;

− находить частные и полный дифференциалы функции многих переменных.

ОК 2. Организовывать собственную деятельность, выбирать типовые методы и способы выполнения профессиональных задач, оценивать их эффективность и качество.

ОК 3. Принимать решения в стандартных и нестандартных ситуациях и нести за них ответственность.

ОК 5. Использовать информационно-коммуникационные технологии в профессиональной деятельности.

Порядок выполнения работы:

1.Повторитьтеоретический материал по теме.

2.Рассмотреть примеры решения типовых заданий.

3. Ответить на контрольные вопросы.

4. Выполнить самостоятельную работу .

5. Сдать отчет по проделанной работе.

Краткие теоретические сведения.

1.Производной от функции по аргументу называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю:

Примечание: производная обозначается также

4.Отыскание производной называется дифференцированием функции.

5.Формулы дифференцирования основных функций:

6.Дифференциалом (первого порядка) функции называется главная часть ее приращения, линейная, относительно приращения аргумента.

Формулы нахождения производной.

Правила вычисления производных:

Примеры решений типовых заданий.

Найти дифференциалы функций.

Решение: Используем основные правила нахождения производных:

Решение: По правилу нахождения производной сложной функции:

Вычислить приближенное значение :

Задания для самостоятельной работы.

Найти дифференциал функции:

1. Вычислить приближенное значение:

_{2 Вариант: задание 1:№4-6}

Практическая работа №4

Тема: « Нахождение экстремумов функций».

Цель: закрепить применение производной к нахождению экстремумов функции, навыки нахождения производной.

При выполнении практической работы студент должен знать:

-определение производной, ее геометрический и механический смысл;

правила и формулы дифференцирования функций;

-определение дифференциала функции и его геометрический смысл; определение второй производной, ее физический смысл;

-необходимые и достаточные условия возрастания и убывания функции, существования экстремума;

общую схему построения графиков функций

После окончания занятия необходимо у меть:

-дифференцировать функции, используя таблицу производных и правила;

-применять производную для нахождения промежутков монотонности и экстремумов функции;

ОК 2. Организовывать собственную деятельность, выбирать типовые методы и способы выполнения профессиональных задач, оценивать их эффективность и качество.

ОК 3. Принимать решения в стандартных и нестандартных ситуациях и нести за них ответственность.

ОК 5. Использовать информационно-коммуникационные технологии в профессиональной деятельности.

ОК 8. Самостоятельно определять задачи профессионального и личностного развития, заниматься самообразованием, осознанно планировать повышение квалификации.

ОК 9. Ориентироваться в условиях частой смены технологий в профессиональной деятельности.

Порядок выполнения работы:

1.Изучить теоретический материал по теме «Нахождение точек экстремума функции».

2.Рассмотреть примеры решения типовых заданий.

3. Ответить на контрольные вопросы.

4. Выполнить самостоятельную работу .

5. Сдать отчет по проделанной работе.

Краткие теоретические сведения.

Алгоритм нахождения экстремумов функции.

1.Найти производную функции и приравнять ее к нулю.

3.Отметить точки максимуму и минимума.

4.Найти значение функции в точках экстремума.

Алгоритм нахождения экстремумов функции с помощью второй производной.

Пример 1.Найти точки экстремума функции

Решение: Найдём критические точки:

Отложим их на числовой прямой и определим знаки производной:
1
точка максимума, так как при переходе через нее производная меняет знак с «+» на «-»

. точка минимума, так как при переходе через нее производная меняет знак с «-» на «+»

Задания для самостоятельной работы.

1.Исследовать функцию на монотонность: у = х 2 +2х-4

3.Исследовать функцию на монотонность и экстремумы.

4. Найти промежутки возрастания и убывания функции:

1.Исследовать функцию на монотонность: у =- х 2 +2х.

3.Исследовать функцию на монотонность и экстремумы.

4.Найти промежутки возрастания и убывания функции: у =

2.Найти точки экстремумов

3.Исследовать функцию на монотонность и экстремумы:

5. Определить экстремумы функции: y =.

Время на выполнение: 90- мин. (час.),

выполнение 1 час.10 мин.;

оформление и сдача 10 мин.

Работа выполняется в тетради для практических работ.

Шкала оценки образовательных достижений

Процент результативности (правильных ответов)

Оценка уровня подготовки

Практическая работа №5

Тема: « Применение различных методов для решения систем линейных уравнений».

Цель: закрепить знания о матрицах и определителях , с формировать умения решать системы алгебраических уравнений первой степени методом Крамера, закрепить знания о матрицах и определителях , с формировать умения решать системы алгебраических уравнений первой степени методом Гаусса

При выполнении практической работы студент должен знать:

После окончания занятия необходимо у меть:

– вычислять определители второго и третьего порядка

– решать СЛАУ методом Гаусса

– решать СЛАУ методом Крамера

ОК 1. Понимать сущность и социальную значимость своей будущей профессии, проявлять к ней

ОК 2. Организовывать собственную деятельность, выбирать типовые методы и способы выполнения профессиональных задач, оценивать их эффективность и качество.

ОК 4. Осуществлять поиск и использование информации, необходимой для эффективного выполнения профессиональных задач, профессионального и личностного развития.

ОК 7. Брать на себя ответственность за работу членов команды (подчиненных), за результат выполнения заданий.

Порядок выполнения работы:

1.Повторить теоретический материал по теме «решение систем уравнений методом Крамера, Гаусса.».

2.Рассмотреть примеры решения типовых заданий.

3. Ответить на контрольные вопросы.

4. Выполнить самостоятельную работу .

5. Сдать отчет по проделанной работе.

Краткие теоретические сведения.

Метод исключения неизвестных (метод Гаусса), основная идея данного метода состоит в том, что данная система линейных уравнений преобразуется в равносильную ей систему специального вида, где одно из уравнений системы содержит все неизвестные, второе – на одно неизвестное меньше, и т. д., последнее уравнение – лишь одно из неизвестных. Покажем это на примере.

Пример. Решить систему линейных уравнений методом Гаусса.

Первый шаг закончен. Второе и третье уравнения образуют первую подсистему. За второе ведущее уравнение примем второе уравнение системы, а за второе ведущее неизвестное – х ₂ ; вторым ведущим элементом будет 7/2. Исключим х ₂ из третьего уравнения. Получим:

Второй шаг закончен. Вторая подсистема состоит из одного третьего уравнения. Прямой ход метода Гаусса закончен. Обратным ходом получаем:

Итак, решение данной системы будет:

Задания для самостоятельной работы.

Вариант 1 ( пример №1,4,а,в. )

Задание 1.Решить по формулам Крамера системы линейных уравнений:

Задание 2.Решить методом Гаусса системы уравнений:

Вариант 2 (пример №2,3, б,г. )

Что называется системой линейных алгебраических уравнений?

Что значит решить систему уравнений.

Сформулируйте теорему Крамера.

Запишите формулы Крамера.

Сформулируйте метод Гаусса.

Время на выполнение: 90- мин. (час.),

выполнение 1 час.10 мин.;

оформление и сдача 10 мин.

Работа выполняется в тетради для практических работ.

Шкала оценки образовательных достижений

Процент результативности (правильных ответов)

Оценка уровня подготовки

Баврин И.И. Математика для технических колледжей и техникумов: учебник и практикум для СПО. – 2-е изд., испр. и доп.. – М.: Юрайт, 2018

Элькин В.Д. Математика и информатика: учебник и практикум для СПО. – М.: Юрайт, 2019

Баврин И.И. Математический анализ: учебник и практикум для СПО. – М.: Юрайт, 2019

Богомолов Н.В., Самойленко П.И. Математика: учебник для СПО. – М.: Юрайт, 2018

Пехлецкий И.Д. Математика: учебник. – М.: ИЦ « Академия», 2018

Математика.(СПО).учебник / М.И. Башмаков. — Москва : КноРус, 2019. — 394 с. —Режим доступа: :индивидуальный круглосуточный доступ к ЭБС из любой точки доступа к сети интернет. Коллекция СПО ЭБС book / ru 26.12.18-26.03.20г.(15 месяцев). https://www.book.ru/book/929528/view2/1

7.Григорьев В.П. Математика (2-е изд., стер.): учебник. – М.: ИЦ « Академия», 2018

8. Кацман Ю.Я. Теория вероятностей и математическая статистика. Примеры с решениями: учебник. – М.: “Юрайт”, 2017

Источник