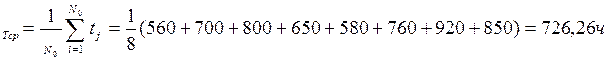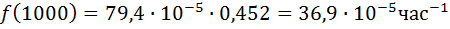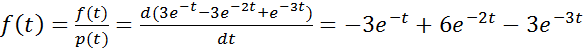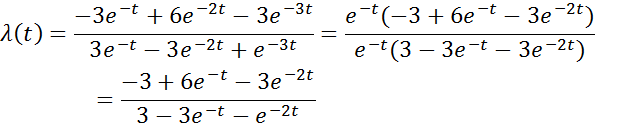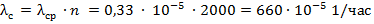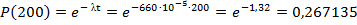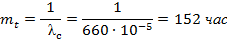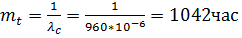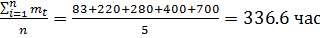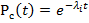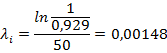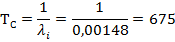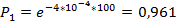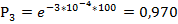Известно что частота отказов изделия аппроксимируется формулой
Требуется определить среднее время восстановления аппаратуры.
Определить статистическую оценку среднего времени безотказной работы изделия.
Стат оценка ср вр-ни безотк работы
62. За наблюдаемый период эксплуатации в аппаратуре было зарегистрировано 6 отказов. Время восстановления составило: t1 =15мин.; t2=20мин.; t3 =10мин.; t4=28мин.; t5=22мин.; t6=30мин.
Требуется определить среднее время восстановления аппаратуры.
Среднее время восстан-ния аппаратуры
63. На испытание поставлено 1000 изделий. За время t=11000 час. вышло из строя 410 изделий. Зв последующий интервал времени 11000-12000 час. вышло из строя еще 40 изделий. Необходимо вычислить p*(t) при t=11000 час. и t=12000 час., а также f*(t), λ *(t) при t=11000 час.
N=1000, T=11000час, Δt=1000час, n(t)=(1000-410)=590, Δn(t)=40.
P * (11000)=n(t)/N = 590/1000=0,59
P * (12000)=n(t)/N = 40/1000=0,04
64. Вероятность безотказной работы автоматической линии изготовления цилиндров автомобильного двигателя в течении 120 час равна 0.9. Предполагается, что справедлив экспоненциальный закон надежности. Требуется рассчитать интенсивность отказов и частоту отказов линии для момента времени t =120 час., а также среднее время безотказной работы.
65. Среднее время безотказной работы автоматической системы управления равно 640 час. Предполагается, что справедлив экспоненциальный закон надежности. Необходимо определить вероятность безотказной работы в течение 120 час., частоту отказов для момента времени t=120 час и интенсивность отказов.
m(t)=640 час, t=120 час.
λ=1/640=1,56 * 10-3 1/час.
P(120)= e —1,56*10-3*120 =0,42
Требуется вычислить количественные характеристики надежности Р(t), f(t), λ(t) для t=150 час. и среднее время безотказной работы шарикоподшипников.
68. Вероятность безотказной работы изделия в течение t=1000 час. Р(1000)=0,95. Время исправной работы подчинено экспоненциальному закону. Требуется определить количественные характеристики надежности f(t), λ (t), mt.
69. Среднее время исправной работы изделия равно 1260 час. Время исправной работы подчинено экспоненциальному закону. Необходимо найти его количественные характеристики надежности P(t), f(t), λ (t) для t=1000 час.
1) 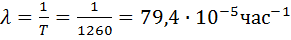
2)Варианты безотказной работы
1)
=1-2 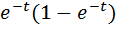
2) 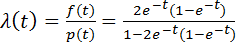
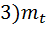

Требуется найти количественные характеристики надежности P(t), λ (t), mt.
f(t)=
1)
2)
3)
72. Определить вероятность безотказной работы и интенсивность отказов прибора при t = 1300 часов работы, если при испытаниях получено значение среднего времени безотказной работы mt=1500 час. и среднее квадратическое отклонение σt = 100 час.
Дано: t=1300 ; mt=1500 час; 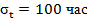
Решение: по эксп. закону 

По нормальному закону: 

λ(t) = f(t)/P(t) = 0,0024 1/час
Необходимо определить вероятность безотказной работы аппаратуры в течении t = 200 час и среднее время безотказной работы аппаратуры.
Решение:
Решение:
2)
3)
При последовательном соединении: Pс(t)=
77. Система состоит из пяти приборов, среднее время безотказной работы которых равно: mt1=83 час; mt2=220 час; mt3=280 час; mt4=400 час; mt5=700 час. Для приборов справедлив экспоненциальный закон надежности. Требуется найти среднее время безотказной работы системы.
Экспоненциальный закон надежности: mср=1/λ
Среднее время безотказной работы системы:
mcр =
78. Прибор состоит из пяти блоков. Вероятность безотказной работы каждого блока в течение времени t=50 час равна: P1(50)=0,98; Р2(50)=0,99; Р3(50)=0,998; Р4(50)=0,975; Р5(50)=0,985. Справедлив экспоненциальный закон надежности. Требуется найти среднее время безотказной работы прибора.
Найдем вероятность безотказной работы системы Рс(t)= 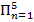
Исходя из экспоненциального закона, найдем интенсивность отказов
Найдем среднюю наработку до первого отказа
Средняя наработка до первого отказа равна 675 часов.
Pc(t)=
mtc=
mtc=
λc(t)=
Известно что частота отказов изделия аппроксимируется формулой
Критерии и количественные характеристики надежности
Критерием надежности называется признак, по которому можно количественно оценить надежность различных устройств.
К числу наиболее широко применяемых критериев надежности относятся:
– вероятность безотказной работы в течение определенного времени P(t);
– средняя наработка до первого отказа Tср;
– наработка на отказ tср;
– частота отказов f(t) или a(t);
– интенсивность отказов l (t);
– параметр потока отказов w (t);
– функция готовности Kг(t);
– коэффициент готовности Kг.
Характеристикой надежности следует называть количественное значение критерия надежности конкретного устройства.
Выбор количественных характеристик надежности зависит от вида объекта.
Критерии надежности невосстанавливаемых объектов
Рассмотрим следующую модель работы устройства.
Пусть в работе (на испытании) находится N0 элементов и пусть работа считается законченной, если все они отказали. Причем вместо отказавших элементов отремонтированные не ставятся. Тогда критериями надежности данных изделий являются:
– вероятность безотказной работы P(t);
– частота отказов f(t) или a(t);
– интенсивность отказов l (t);
– средняя наработка до первого отказа Tср.
Вероятностью безотказной работы называется вероятность того, что при определенных условиях эксплуатации в заданном интервале времени или в пределах заданной наработки не произойдет ни одного отказа.
Вероятностью отказа называется вероятность того, что при определенных условиях эксплуатации в заданном интервале времени возникает хотя бы один отказ. Отказ и безотказная работа являются событиями несовместными и противоположными, поэтому
Q(t)=P(T £ t), 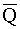
Частотой отказов по статистическим данным называется отношение числа отказавших элементов в единицу времени к первоначальному числу работающих (испытываемых) при условии, что все вышедшие из строя изделия не восстанавливаются.
Частота отказов есть плотность вероятности (или закон распределения) времени работы изделия до первого отказа. Поэтому
Интенсивностью отказов по статистическим данным называется отношение числа отказавших изделий в единицу времени к среднему числу изделий, исправно работающих в данный отрезок времени.
Вероятностная оценка характеристики l (t) находится из выражения
l (t) = f(t) / P(t). (4.2.7)
Интенсивность отказов и вероятность безотказной работы связаны между собой зависимостью
P(t) = еxp 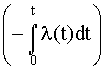
Средней наработкой до первого отказа называется математическое ожидание времени работы элемента до отказа.
Как математическое ожидание, Tср вычисляется через частоту отказов (плотность распределения времени безотказной работы):
M[t] = Tcр = 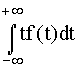
Так как t положительно и P(0)=1, а P( ¥ )=0, то
Tcр = 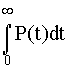
По статистическим данным об отказах средняя наработка до первого отказа вычисляется по формуле
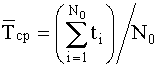
Как видно из формулы (4.2.11), для определения средней наработки до первого отказа необходимо знать моменты выхода из строя всех испытуемых элементов. Поэтому для вычисления средней наработки на отказ 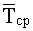
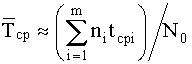
Из выражений для оценки количественных характеристик надежности видно, что все характеристики, кроме средней наработки до первого отказа, являются функциями времени. Конкретные выражения для практической оценки количественных характеристик надежности устройств рассмотрены в разделе “Законы распределения отказов”.
Средняя наработка до первого отказа является достаточно наглядной характеристикой надежности. Однако применение этого критерия для оценки надежности сложной системы ограничено в тех случаях, когда:
– время работы системы гораздо меньше среднего времени безотказной работы;
– закон распределения времени безотказной работы не однопараметрический и для достаточно полной оценки требуются моменты высших порядков;
– система резервированная;
– интенсивность отказов не постоянная;
– время работы отдельных частей сложной системы разное.
Рассмотрим следующую модель работы.
Пусть в работе находится N элементов и пусть отказавшие элементы немедленно заменяются исправными (новыми или отремонтированными). Если не учитывать времени, потребного на восстановление системы, то количественными характеристиками надежности могут быть параметр потока отказов w (t) и наработка на отказ tср.
Параметром потока отказов называется отношение числа отказавших изделий в единицу времени к числу испытываемых при условии, что все вышедшие из строя изделия заменяются исправными (новыми или отремонтированными).
Параметр потока отказов и частота отказов для ординарных потоков с ограниченным последействием связаны интегральным уравнением Вольтера второго рода
w (t) = f(t)+ 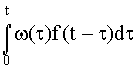
По известной f(t) можно найти все количественные характеристики надежности невосстанавливаемых изделий. Поэтому (2.14) является основным уравнением, связывающим количественные характеристики надежности невосстанавливаемых и восстанавливаемых элементов при мгновенном восстановлении.
Уравнение (4.2.14) можно записать в операторной форме:
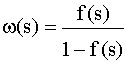
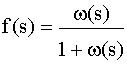
Соотношения (4.2.15) позволяют найти одну характеристику через другую, если существуют преобразования Лапласа функций f(s) и w (s) и обратные преобразования выражений (4.2.15).
Это свойство параметра потока отказов позволяет утверждать, что при вычислении количественных характеристик надежности сложной системы нельзя суммировать имеющиеся в настоящее время значения интенсивности отказов элементов, полученных по статистическим данным об отказах изделий в условиях эксплуатации, так как указанные величины являются фактически параметрами потока отказов;
Из рассмотрения свойств интенсивности и параметра потока отказов видно, что эти характеристики различны.
В настоящее время широко используются статистические данные об отказах, полученные в условиях эксплуатации оборудования. При этом они часто обрабатываются таким образом, что приводимые характеристики надежности являются не интенсивностью отказов, а параметром потока отказов w (t). Это вносит ошибки при расчетах надежности. В ряде случаев они могут быть значительными.
Для получения интенсивности отказов элементов из статистических данных об отказах ремонтируемых систем необходимо воспользоваться формулой (4.2.6), для чего необходимо знать предысторию каждого элемента технологической схемы. Это может существенно усложнить методику сбора статистических данных об отказах. Поэтому целесообразно определять l (t) по параметру потока отказов w (t). Методика расчета сводится к следующим вычислительным операциям:
– по статистическим данным об отказах элементов ремонтируемых изделий и по формуле (4.2.13) вычисляется параметр потока отказов и строится гистограмма w i(t);
– гистограмма заменяется кривой, которая аппроксимируется уравнением;
– находится преобразование Лапласа w i(s) функции w i(t);
– по известной w i(s) на основании (4.2.15) записывается преобразование Лапласа fi(s) частоты отказов;
– по известной fi(s) находится обратное преобразование частоты отказов fi(t);
– находится аналитическое выражение для интенсивности отказов по формуле
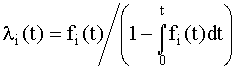
– строится график l i(t).
Если имеется участок, где l i(t)= l i=const, то постоянное значение интенсивности отказов принимается для оценки вероятности безотказной работы. При этом считается справедливым экспоненциальный закон надежности.
Наработка на отказ является достаточно наглядной характеристикой надежности, поэтому она получила широкое распространение на практике.
Часто коэффициент готовности, вычисленный по формуле (4.2.26), отождествляют с вероятностью того, что в любой момент времени восстанавливаемая система исправна. На самом деле указанные характеристики неравноценны и могут быть отождествлены при определенных допущениях.
Действительно, вероятность возникновения отказа ремонтируемой системы в начале эксплуатации мала. С ростом времени t эта вероятность возрастает. Это означает, что вероятность застать систему в исправном состоянии в начале эксплуатации будет выше, чем после истечения некоторого времени. Между тем на основании формулы (4.2.26) коэффициент готовности не зависит от времени работы.
Для выяснения физического смысла коэффициента готовности Kг запишем формулу для вероятности застать систему в исправном состоянии. При этом рассмотрим наиболее простой случай, когда интенсивность отказов l и интенсивность восстановления m есть величины постоянные.
Предполагая, что при t=0 система находится в исправном состоянии (P(0)=1), вероятность застать систему в исправном состоянии определяется из выражений
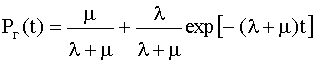
(4.2.27)
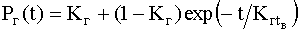
где l = 1 / Tср; m =1 / tв; Kг = Тср / (Тср+ tв).
Это выражение устанавливает зависимость между коэффициентом готовности системы и вероятностью застать ее в исправном состоянии в любой момент времени t.
РФ. Решение. Среднее время безотказной работы изделия по статистическим данным оценивается выражением
Оценка надежности изделия
t1 =560час.; t2=700час.; t3 =800час.; t4=650час.; t5=580час.; t6=760час.; t7=920час.; t8=850час. Определить статистическую оценку среднего времени безотказной работы изделия.
Среднее время безотказной работы изделия по статистическим данным оценивается выражением
Решение. Данная задача является частным случаем решённой в Методических указаниях задачи 2.5, где частота отказов имеет вид
Вероятность безотказной работы:
Зависимость интенсивности отказов от времени:
Определим среднее время безотказной работы аппаратуры:
Решение. Интенсивность отказов системы:
Вероятность безотказной работы электронной машины:
Среднее время безотказной работы электронной машины:
бозотказный работа надежность профилактический
Задача 4.12. Нерезервированная система управления состоит из n = 4000 элементов. Известна требуемая вероятность безотказной работы системы Рс(t) = 0,9 при t = 100 час. Необходимо рассчитать допустимую среднюю интенсивность отказов одного элемента, считая элементы равнонадежными, для того чтобы приближенно оценить достижение заданной вероятности безотказной работы при отсутствии профилактических осмотров в следующих случаях: а) резервирование отсутствует ; б) применено общее дублирование.
Решение. а) резервирование отсутствует
В случае экспоненциального закона надежности всех элементов системы для интенсивности отказов одного элемента имеем
. Интенсивность отказов для всей системы равна
; вероятность безотказной работы системы при t = 100 час. Равна
Отсюда находим интенсивность отказов одного элемента:
б) применено общее ду6лирование
Решение. В рассматриваемом случае кратность резервирования m = 1.

Среднее время безотказной работы устройства:

Задача 6.9. Радиоэлектронная аппаратура состоит из трех блоков:
Вероятность безотказной работы аппаратуры при отсутствии резервирования равна
б) в случае, если имеется дублирование каждого блока, вероятность безотказной работы аппаратуры равна