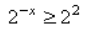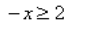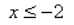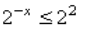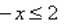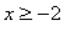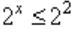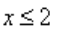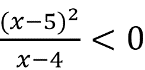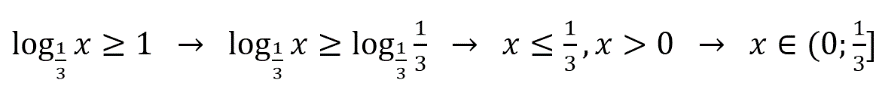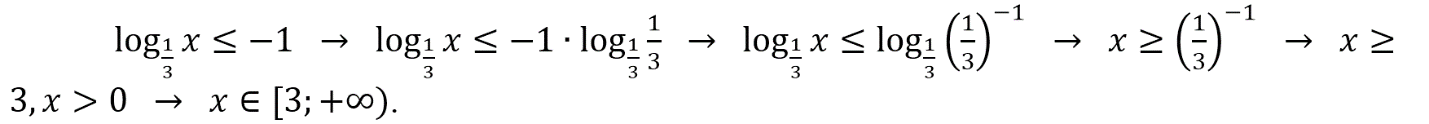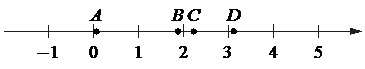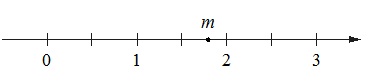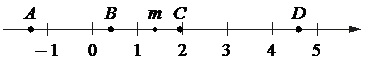Известно что число n принадлежит промежутку 1 0

Курс подготовки к ОГЭ по математике

Онлайн-конференция

«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»

Свидетельство и скидка на обучение каждому участнику

Итоговая работа по теме: «Разработка системы итогового повторения курса алгебры 7-9 классов»

На подготовку к экзамену по математике в 9 классе дополнительно выделяется 1 час консультации в неделю, 32 часа в год, из них 12 часов на подготовку по алгебре, 16 часов на подготовку по геометрии и 4 часа на подготовку по теории вероятностей. Также в конце года на итоговое повторение выделяется 30 часов. Итого для итогового повторения курса алгебры 7-9 классов 42 часа. Повторение я разбила на темы, после каждой темы проверочная работа в форме теста.

Планирование учебного материала

Установите соответствие между выражениями и их значениями:

В таблице приведены значения радиусов атомов четырех химических элементов. Какой из этих элементов имеет наименьший атомный радиус?

В таблице приведены нормативы по прыжкам с места в длину для учащихся начальных классов.

5 2) норматив не выполнен 3) 4 4) 3

Семья из двух взрослых и трех детей отправилась в путешествие по реке на теплоходе. Билет для взрослого стоит 3000 рублей, для ребенка делается скидка 25%. Найдите стоимость всех билетов. Ответ дайте в рублях.

Укажите наибольшее из чисел:

Между какими соседними целыми числами расположено число?

2) 3) 4) все эти числа.

Магазин «Малыш» закупает на оптовой базе наборы погремушек. Стоимость одного набора 145 рублей. Если общая сумма превышает 1000 рублей, то на ту часть суммы, которая превышает 1000 рублей, дается скидка 40%. Сколько рублей магазин должен будет перечислить на счет оптовой базы при заказе 14 наборов?

Найдите координату точки А

На координатной прямой отмечено число с

Из следующих неравенств выберите верное:

1)с-4 2) 5-с 3) 3-с 4) с-6

Известно, что число р принадлежит промежутку (-1;0). В каком из указанных случаев точки с координатами р; 2р; р 2 расположены на координатной прямой в правильном порядке?

Какое из чисел отмечено на координатной прямой точкой В?

На координатной прямой отмечены числа р и с.

Какое из следующих неравенств верное?

Какое из чисел отмечено на координатной прямой точкой Р?

78 и 80 2) 8 и 9 3) 7 и 8 4) 9 и 10

Найдите значение выражения при a =8, b =3.

При каком значении переменной х значение выражения х+ является числом рациональным:

при х=13 2) при х=14 3) при х=15 4) при х=16

При каком значении х выражение не имеет смысла:

при х=4 и при х=10 2) при х=4 и при х=0 3) при х=4 4) при х=10

Какие из данных выражений тожественно равны произведению (х-7)(9х+1):

Найдите значение выражения при х=

Разложите на множители у 2 – ху 2 +ху – у.

Для каждого из выражений укажите тождественно равное ему:

0,000015 2) 0,000225 3)0,00015 4)0,00225

Представьте выражение в виде степени с основанием х

примерно в 18 раз 2) примерно в 180 раз 3) примерно в 1,8 раза 4) примерно в 5,6 раза

Какое из следующих выражений равно произведению 25∙5 n

125 n 2)25 n 3) 5 2n 4) 5 n+2

Решите уравнения: а) х 2 – х – 20=0; б) х + =; в) (2х – 5)(х+3)=0 г) х 2 –8х=0 д) х 2 – 16=0

Какое из данных уравнений не имеет корней:

х 2 +5х + 1=0 2) х 2 –2х + 1=0 3) х 2 + х – 2=0 4) х 2 + х + 5=0

Решите систему уравнений:

Найдите координаты точек пересечения параболы у=х 2 – 3х + 3 и прямой 2х – у – 1 =0.

Огурцы дешевле помидоров на 50%. На сколько процентов помидоры дороже огурцов?

Теплоход проходит по течению реки до пункта назначения 160 км и после стоянки возвращается в пункт отправления. Найдите скорость течения, если скорость теплохода в стоячей воде равна 18 км/ч, стоянка длится 2 часа, а в пункт отправления теплоход возвращается ровно через 20 часов после отплытия из него.

Сопоставьте неравенства и множества их решений.

Найдите область определения выражения

Последовательность задана формулой а _n = 6 n +4. Какое из указанных чисел является членом этой последовательности?

-24 2) 11 3) 40 4) 121

6; 7; 9; 12;… 2) 2; 4; 8; 16;… 3) 2; 4; 6; 8;… 4)3; 1; ;…

6; 7; 9; 1 1 ;… 2) 2; 4; 8; 16;… 3) 2; 4; 6; 12 ;… 4); ;…

Последовательность ( а _n ) – арифметическая прогрессия. Найдите сумму первых одиннадцати ее членов, если а ₁ =12, а ₂ =10.

Последовательность ( а _n ) – арифметическая прогрессия. Найдите сумму первых пятнадцати ее членов, если а ₃ = 9, а ₄ =5.

Последовательность ( b _n ) – геометрическая прогрессия. Найдите сумму первых пяти ее членов, если b ₂ =5, b ₃ =10.

Дана арифметическая прогрессия 36; 27; 18;… Найдите первый отрицательный член этой прогрессии.

15 + 3 n 2) 3 n 3) 9 + 3 n 4) 12 + 3 n

Последовательность задана формулой b _n =. Сколько членов этой последовательности больше двух?

График какой из приведенных ниже функций изображен на рисунке?

Установите соответствие между графиками функций и формулами, которые их задают.

Найдите область определения функции у =

х3 2) х3 3) х0 4) х – любое число

А) k 0, b Б) k 0, b В) k 0, b

1) a 0, c 2) a 0, c 3) a 0, c 4) a0, c

на каком расстоянии друг от друга были автобус и такси в 18 часов; 3) на каком расстоянии от города произошла встреча автобуса и такси.

Найдите значение выражения

a+b 2) – a 3) 2b 4) a – b

Решите уравнение х 2 + 8х + 16=0

Упростите выражение ( t + 3) 2 – (6 t – 1) и найдите его значение при t =2

Найдите наименьшее целое решение системы неравенств

Решите уравнение х 3 – 6х 2 – 4х + 24 =0

Решите систему неравенств

Катер прошел от одной пристани до другой, расстояние между которыми по реке равно 48 км, сделал стоянку на 20 мин и вернулся обратно через 5 ч после начала поездки. Найдите скорость течения реки, если известно, что скорость катера в стоячей воде равна 20 км/ч.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

Ищем педагогов в команду «Инфоурок»

Номер материала: ДБ-029460

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

НИУ ВШЭ откроет первую в России магистратуру по управлению низкоуглеродным развитием

Время чтения: 2 минуты

В Петербурге школьникам разрешили уйти на каникулы с 25 декабря

Время чтения: 2 минуты

Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст

Время чтения: 1 минута

В России утвердили новый порядок формирования федерального перечня учебников

Время чтения: 1 минута

Апробацию новых учебников по ОБЖ завершат к середине 2022 года

Время чтения: 1 минута

Путин поручил не считать выплаты за классное руководство в средней зарплате

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник

Задание №17 ЕГЭ по математике базового уровня

Неравенства и сравнения

В семнадцатом задании нам необходимо сравнить данные числа с положением на координатной прямой или решить и сопоставить решения неравенств с областью на прямой. В данном задании можно пользоваться правилом исключения, поэтому достаточно правильно определить три решения из четырех, выбирая в первую очередь простые. Итак, приступим к разбору 17 задания базового варианта ЕГЭ по математике.

Разбор типовых вариантов заданий №17 ЕГЭ по математике базового уровня

Вариант 17МБ1

Каждой точке соответствует одно из чисел в правом столбце. Установите соответствие между указанными точками и числами.

Алгоритм выполнения:

Решение:

Логарифм по основанию a от аргумента x — это степень, в которую надо возвести число a, чтобы получить число x.

Вариант 17МБ2

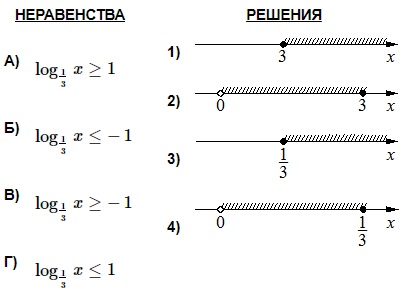
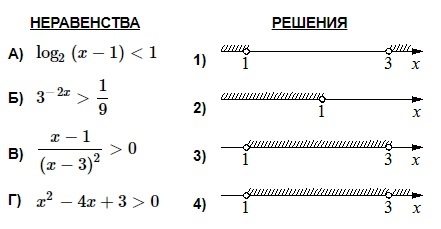
Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.

НЕРАВЕНСТВА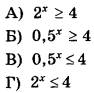

РЕШЕНИЯ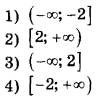

Алгоритм выполнения:

Решение:

Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.

Неравенство примет вид:

Основания степеней одинаковы, следовательно, степени соотносятся так же.

то есть, 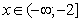— вариант под номером 1.

Аналогично с вариантом Б.

Неравенство примет вид:

Основания степеней одинаковы, следовательно, степени соотносятся так же.

то есть, 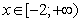— вариант под номером 4.

Представим 4 в виде степени с основанием 2. 2 2 = 4.

Неравенство примет вид:

Основания степеней одинаковы, следовательно, степени соотносятся так же.

и 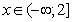— вариант под номером 3.

Вариант 17МБ3

Каждому из четырёх чисел в левом столбце соответствует отрезок, которому оно принадлежит. Установите соответствие между числами и отрезками из правого столбца.

ЧИСЛА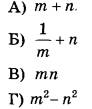

ОТРЕЗКИ

Алгоритм выполнения:

Решение:

Вариант 17МБ4

Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.

Рассмотрим первое неравенство:

Вариант 17МБ5

Каждому из четырех неравенств в левом столбце соответствует одно из решений в правом столбце. Установить соответствие между неравенствами и их решениями.

Алгоритм выполнения

Решение:

А. 2 –х+1 –x+1 –1 → –x+1 2. Ответ: х ϵ (2; +∞). Получаем: А–3.

Б.

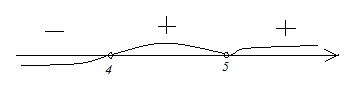
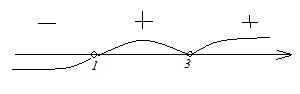
Неравенство преобразований не требует, поэтому сразу применяем метод интервалов, отобразив корни неравенства на координатной прямой.

Корни в данном случае – это х=4 и х=5. Имеем в виду, что неравенство строгое, т.е. значения корней в промежуток для ответа не включаем. В точке х=5 перехода знака не происходит, т.к. по условию (х–5) дано в квадрате. Поскольку нам нужен промежуток, где х 1 → log₄x > log₄4 → x > 4. Т.е.: х ϵ (4; +∞). Ответ: В–1.

Вариант 17МБ6

На координатной прямой отмечены точки А, В, С и D.

Каждой точке соответствует одно из чисел в правом столбце. Установите соответствие между указанными точками и числами.

Алгоритм выполнения

Для каждого из выражений правого столбца делаем следующее:

Решение:

Это значение на прямой находится между значениями –3 и –2 и соответствует точке А. Получили: А–1.

Число находится между значениями 2 и 3 и соответствует точке D. Имеем: D–2.

Число находится на прямой между 0 и 1. Это – точка С. Имеем: С–3.

Число размещается на прямой между значениями –1 и 0, что отображает т.В. Получаем: В–4.

Вариант 17МБ7

Каждому из четырех неравенств в левом столбце соответствует одно из решений в правом столбце. Установить соответствие между неравенствами и их решениями.

Алгоритм выполнения

Решение:

А.

Полученный промежуток-ответ отображен на 4-й координатной прямой. Поэтому имеем: А–4.

Полученный промежуток представлен на 1-й прямой. Отсюда имеем: Б–1.

В. Это неравенство аналогично предыдущему (Б) с разницей исключительно в знаке. Поэтому и ответ будет подобен с той только разницей, что в конечном неравенстве будет противоположный знак. Т.е. получим: х ≤ 3, х > 0 → x ϵ (0; 3]. Соответственно, получаем пару: В–2.

Г. Это неравенство аналогично 1-му (А), но с противоположным знаком. Поэтому ответ здесь будет таким: х ≥ 1/3, х > 0 → х ϵ [1/3; +∞). Т.о., ответ: Г–3.

Вариант 17МБ8

Каждому из четырех неравенств в левом столбце соответствует одно из решений в правом столбце. Установить соответствие между неравенствами и их решениями.

Алгоритм выполнения

Решение:

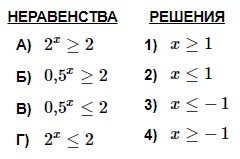
А. 2 х ≥ 2 → 2 х ≥ 2 1 → х ≥ 1. Имеем: А–1.

Г. По аналогии с неравенством А получаем в ответе: х ≤ 1. Имеем: Г–2.

Б. 0,5 х ≥ 2 → (1/2) х ≥ 2 →2 –х ≥ 2 1 х ≤ –1. Имеем: Б–3.

В. По аналогии с неравенством Б получаем в ответе: х ≥ –1. Имеем: В–4.

Вариант 17МБ9

Каждому из четырех неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.

Алгоритм выполнения

Решение:

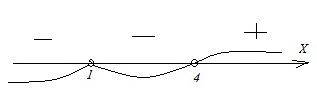
Корнями в этих неравенствах являются х=1 и х=4.

Для неравенства А на прямой имеем:

Результатом здесь будут промежутки с отрицательным знаком, т.е. х 4. Ответ: Б–1.

В неравенстве В нужно взять промежуток с отрицательным знаком. Тогда имеем: 1 4. Ответ: Г–2.

Вариант 17МБ10

На координатной прямой отмечены точки А, В, С и D.

Каждой точке соответствует одно из чисел в правом столбце. Установите соответствие между указанными точками и числами.

Алгоритм выполнения

Решение:

Вариант 17МБ11

Каждому из четырех неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.

Алгоритм выполнения

Решение:

Объединяем полученный промежуток с ОДЗ, получаем: x ϵ (1; 3). Это соответствует решению №3. Ответ: А–3.

Тогда в результате имеем: х ϵ (1; +∞). Ответ: Б–2.

Для решения требуется взять промежутки с положительным знаком. ОДЗ: х≠3. Получаем: х ϵ (1; 3)ᴗ(3; +∞). Ответ: В–4.

ОДЗ не дает ограничений. Значит, х ϵ (–∞; 1)ᴗ(3; +∞). Ответ: Г–1.

Вариант 17МБ12

На координатной прямой отмечено число m.

Каждому из четырех чисел в левом столбце соответствует отрезок, которому оно принадлежит. Установите соответствие между числами и отрезками из правого столбца.

Алгоритм выполнения

Решение:

Число m располагается на прямой между 1,5 и 2 и немного смещено от середины этого отрезка к двойке. Следовательно, наиболее точным для него является 1,8.

Число А. Имеем: √1,8. Известно, что √1=1, √2≈1,4. Т.е. √1,8 наверняка располагается на отрезке между 1 и 2. Ответ: А–1.

Число Б. Оно равно: 1,8 3 =5,832, т.е. это число принадлежит промежутку [5; 6]. Ответ: Б–4.

Число В. Это число равно: 1,8+1=2,8, что соответствует отрезку [2; 3]. Ответ: В–2.

Число Г. Тут получаем: 6/1,8≈3,33. Этому значению соответствует отрезок [3; 4]. Ответ: Г–3.

Вариант 17МБ13

Каждому из четырех чисел в левом столбце соответствует отрезок, которому оно принадлежит. Установите соответствие между числами и отрезками из правого столбца.

Алгоритм выполнения

Решение:

Число √0,15 очень немногим отличается от √0,16, а из 0,16 можно точно извлечь

Находим значения выражений А–Г и определяем их соответствия отрезкам:

А. –1/0,4=–2,5. Результат соответствует отрезку [–3; –2]. Ответ: А–1.

Б. 0,4 2 =0,16. Число входит в промежуток [0; 1]. Ответ: Б–3.

В. 4·0,4=1,6. Это число находится в интервале [1; 2]. Ответ: В–4.

Г. 0,4–1=–0,6. Результат попадает на отрезок [–1; 0]. Ответ: Г–2.

Вариант семнадцатого задания 2019 года (10)

На координатной прямой отмечено число m и точки А, В, С и D.

Каждой точке соответствует одно из чисел в правом столбце. Установите соответствие между указанными точками и числами.

Алгоритм выполнения

Решение:

Точка m располагается почти посередине между 1 и 2, но немного ближе к 1, чем к 2. Максимально приближенным к реальному в данном случае следует считать значение m=1,4.

Определяем соответствие чисел и точек на прямой:

Источник

Информатика ЕГЭ 15 задание разбор

15 задание ЕГЭ «Основные законы алгебры логики»

15-е задание: «Основные законы алгебры логики»
Уровень сложности — повышенный,
Требуется использование специализированного программного обеспечения — нет,
Максимальный балл — 1,
Примерное время выполнения — 5 минут.

Проверяемые элементы содержания: Знание основных понятий и законов математической логики

Плейлист видеоразборов задания на YouTube:

Задания с множествами

Элементами множества А являются натуральные числа. Известно, что выражение

Ответ: 12

Элементами множества А являются натуральные числа. Известно, что выражение

Ответ: 18

Определите наибольшее возможное количество элементов в множестве A .

Ответ: 7

Элементами множества А являются натуральные числа. Известно, что выражение

Определите наименьшее возможное количество элементов множества A.

Ответ: 1

Задания с отрезками на числовой прямой

Отрезки на числовой прямой:

На числовой прямой даны два отрезка: P=[44,48] и Q=[23,35].

Укажите наибольшую возможную длину отрезка А, для которого формула

тождественно ложна, то есть принимает значение 0 при любом значении переменной x.

Ответ: 4

✎ Решение 2 (программирование):
Внимание! этот способ подходит НЕ для всех заданий с отрезками!
Python:

def f(a1,a2,x): return((44 maxim: maxim=a2-a1 print(a1,a2, a2-a1) # сами точки отрезка и длина

PascalABC.net:

Отрезки на числовой прямой:

На числовой прямой даны два отрезка: P = [10,20] и Q = [30,40].

Укажите наибольшую возможную длину отрезка A, для которого формула

тождественно истинна, то есть принимает значение 1 при любом значении переменной x.

Ответ: 10

Отрезки на числовой прямой:

На числовой прямой даны два отрезка: P = [3, 20] и Q = [6, 12].

Укажите наибольшую возможную длину отрезка A, для которого формула

тождественно истинна, то есть принимает значение 1 при любом значении переменной x.

Ответ: 8

Далее возможно 2 способа решения.

✎ 2 способ:
После того, как мы избавились от импликации, имеем:

Отрезки на числовой прямой:

На числовой прямой даны два отрезка: P = [11, 21] и Q = [15, 40].

Укажите наибольшую возможную длину отрезка A, для которого формула

тождественно истинна, то есть принимает значение 1 при любом значении переменной x.

Ответ: 19

Задания с ДЕЛ

Поиск наибольшего А, известная часть Дел ∨ Дел = 1

Для какого наибольшего натурального числа А формула

тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной х)?

Ответ: 8

Далее можно решать задание либо с помощью кругов Эйлера, либо с помощью логических рассуждений.

Решение с помощью логических рассуждений:

Решение с помощью кругов Эйлера:

Результат: 8

✎ Решение 2 (программирование):
Python:

for A in range(1,500): OK = 1 for x in range(1,1000): OK *= ((x % 40 == 0) or (x % 64 == 0))

Поиск наименьшего А, известная часть Дел ∧ ¬Дел = 1

Для какого наименьшего натурального числа А формула

тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной х)?

Ответ: 3

Избавимся от импликации:

✎ Решение 2 (программирование). Язык Python, Pascal:

Из общего выражения:

for A in range(1,50): OK = 1 for x in range(1,1000): OK *= (x % A == 0) 0)or (x mod 42 = 0)) = false then begin ok := 0; break; end; end; if (ok = 1) then begin print(A); break; end end; end.

Результат: 3

Для какого наименьшего натурального числа А формула

тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной х)?

Ответ: 285

✎ Решение 2 (программирование):
Python:
Из общего выражения:

Источник