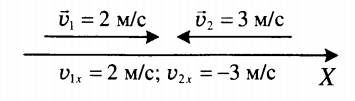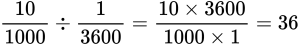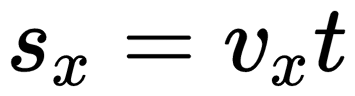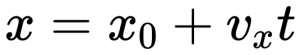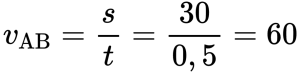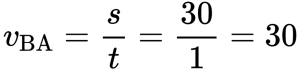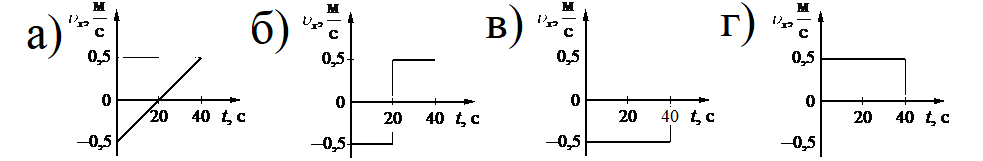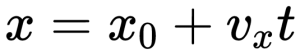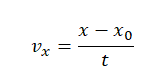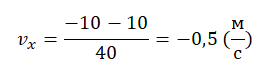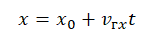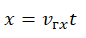Известно что для определения координаты прямолинейно движущегося прямолинейно

Равномерное прямолинейное движение

теория по физике 🧲 кинематика

Равномерное прямолинейное движение — это такое движение, при котором тело совершает за любые равные промежутки времени равные перемещения.

Скорость при прямолинейном равномерном движении

Если тело движется равномерно и прямолинейно, его скорость остается постоянной как по модулю, так и по направлению. Ускорение при этом равно нулю.

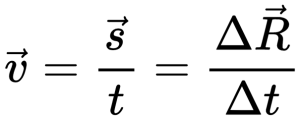
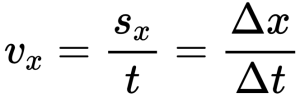
Векторный способ записи скорости при равномерном прямолинейном движении:s — вектор перемещения, ΔR— изменение радиус-вектора, t — время, а ∆t — его изменение. Проекция скорости на ось ОХ: s_x — проекция перемещения на ось ОХ, ∆x — изменение координаты точки (ее абсциссы). Знак модуля скорости зависит от направления вектора скорости и оси координат:

Основная единица измерения скорости — 1 метр в секунду. Сокращенно — 1 м/с.

Спидометр — прибор для измерения модули скорости тела.

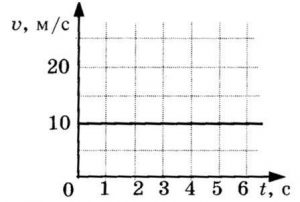
График зависимости скорости от времени представляет собой прямую линию, перпендикулярную оси скорости и параллельную оси времени. Выглядит он так:

Чтобы сравнить модули скоростей на графике, нужно оценить их удаленность от оси времени. Чем дальше график от оси, тем больше модуль.

Пример №1. Найти модуль скорости и направление движения тела относительно оси ОХ. Выразить скорость в км/ч.

График скорости пересекает ось в точке со значением 10. Единица измерения — м/с. Поэтому модуль скорости равен 10 м/с. График лежит выше оси времени. Это значит, что тело движется по направлению оси ОХ. Чтобы выразить скорость в км/ч, нужно перевести 10 м в километры и 1 с в часы:

Теперь нужно разделить километры на часы:

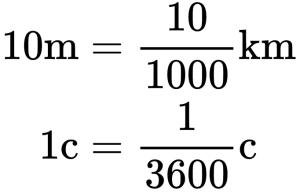
Перемещение и координаты тела при равномерном прямолинейном движении

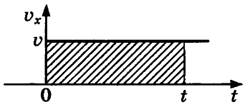
Геометрический смысл перемещения заключается в том, что его модуль равен площади фигуры, ограниченной графиком скорости, осями скорости и времени, а также линией, проведенной перпендикулярно оси времени.

При прямолинейном равномерном движении эта фигура представляет собой прямоугольник. Поэтому модуль перемещения вычисляется по следующей формуле:

Вектор перемещения равен произведению вектора скорости на время движения: Внимание!

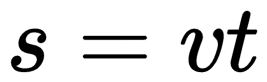
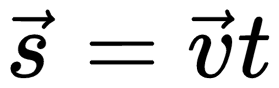
При равномерном прямолинейном движении путь и перемещение совпадают. Поэтому путь, пройденный телом, можно найти по этим же формулам.

Формула проекции перемещения:

График проекции перемещения

График проекции перемещения показывает зависимость этой проекции от времени. При прямолинейном равномерном движении он представляет собой луч, исходящий из начала координат. Выглядит он так:

Чтобы по графику проекции перемещения сравнить модули скоростей, нужно сравнить углы их наклона к оси s_x.Чем меньше угол, тем больше модуль. Согласно рисунку выше, модули скорости тел, которым соответствуют графики 1 и 3, равны. Они превосходят модуль скорости тела 2, так как их угол наклона к оси s_x меньше.

График координаты

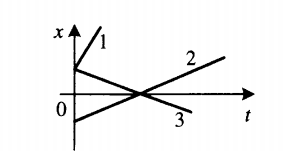
График координаты представляет собой график зависимости координаты от времени. Выглядит он так:

Так как график координаты представляет собой график линейной функции, уравнение координаты принимает вид :

Чтобы сравнить модули скоростей тел по графику координат, нужно сравнить углы наклона графика к оси координат. Чем меньше угол, тем больше модуль скорости. На картинке выше наибольший модуль скорости соответствует графику 1. У графиков 2 и 3 модули равны.

Чтобы по графику координат найти время встречи двух тел, нужно из точки пересечения их графиков провести перпендикуляр к оси времени.

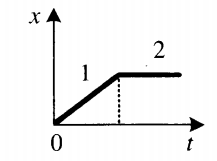
Пример №2. График зависимости координаты тела от времени имеет вид:

Изучите график и на его основании выберите два верных утверждения:

На участке 1 координата растет, и ее график представляет собой прямую. Это значит, что на этом участке тело движется равномерно (с постоянной скоростью). На участке 2 координата с течением времени не меняется, что говорит о том, что тело покоится. Исходя из этого, верными утверждениями являются номера 1 и 3.

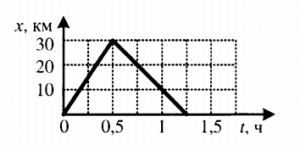
Пример №3. На рисунке изображен график движения автомобиля из пункта А (х=0 км) в пункт В (х=30 км). Чему равна минимальная скорость автомобиля на всем пути движения туда и обратно?

Согласно графику, с начала движения до прибытия автомобиля в пункт 2 прошло 0,5 часа. А с начала движения до возвращения в пункт А прошло 1,5 часа. Поэтому время, в течение которого тело возвращалось из пункта В в пункт А, равно:

Туда и обратно автомобиль проходил равные пути, каждый из которых равен 30 км. Поэтому скорость во время движения от А к В равна:

Скорость во время движения от В к А равна:

Минимальная скорость автомобиля на всем пути движения составляет 30 км/ч.

На рисунке представлены графики зависимости пройденного пути от времени для двух тел. Скорость второго тела v₂ больше скорости первого тела v₁ в n раз, где n равно…

Алгоритм решения

Решение

Рассмотрим графики во временном интервале от 0 до 4 с. Ему соответствуют следующие данные:

Скорость определяется формулой:

Так как начальный момент времени и скорость для обоих тел нулевые, формула примет вид:

Скорость первого тела:

Скорость второго тела:

Отношение скорости второго тела к скорости первого тела:

pазбирался: Алиса Никитина | обсудить разбор | оценить

На рисунке приведён график зависимости координаты тела от времени при прямолинейном движении тела по оси Ox.

Алгоритм решения

Уравнение координаты при равномерном прямолинейном движении имеет вид:

Отсюда проекция скорости равна:

Начальная координата x_o = 10 м, конечная x = –10 м. Общее время, в течение которого двигалось тело, равно 40 с.

Вычисляем проекцию скорости:

Этому значению соответствует график «в».

pазбирался: Алиса Никитина | обсудить разбор | оценить

Алгоритм решения

Решение

Весь график можно поделить на 3 участка:

По условию задачи нужно найти путь, пройденный автомобилем в интервале времени от t₁ = 20 c до t₂ = 50 с. Этому времени соответствуют два участка:

Записываем формулу искомой величины:

s₁ — путь тела, пройденный на первом участке, s₂ — путь тела, пройденный на втором участке.

s₁и s₂ можно выразить через формулы пути для равномерного и равноускоренного движения соответственно:

Теперь рассчитаем пути s₁и s₂, а затем сложим их:

pазбирался: Алиса Никитина | обсудить разбор | оценить

Источник

Известно что для определения координаты прямолинейно движущегося прямолинейно

Школьник летом на даче жил недалеко от военного аэродрома, на который постоянно садились военно-транспортные самолеты, которые летели всегда по одной и той же траектории («глиссаде»), проекция которой на землю являлась прямой линией, отстоящей на расстояние от дачи школьника. Он вооружился секундомером и точным угломерным инструментом, провел многократные измерения некоторых времен и углов и усреднил их для однотипных марок самолетов. Оказалось, что когда самолет находился на минимальном расстоянии от школьника, угол между горизонталью и направлением на самолет составлял а а звук его двигателей был слышен в месте нахождения школьника спустя время За это время самолет успевал удалиться от точки максимального сближения со школьником на угловое расстояние Исходя из этих данных, школьник определил скорость самолета. Чему она оказалась равна?

Какие законы Вы использовали для описания движения? Обоснуйте их применение к данному случаю.

Обоснование. Движение самолета является поступательным, поэтому самолет можно считать материальной точкой и рассматривать перемещение в вертикальной плоскости. Учитывая, что промежуток времени очень мал, можно считать за данный интервал времени движение самолета прямолинейным и равномерным и применять законы данного вида движения.

Перейдем к решению. Поскольку угол наклона глиссады мал, то в момент максимального сближения самолета и школьника расстояние между ними примерно равно

где l — раcстояние до глиссады.

Звук от двигателей, излученный в этот момент, доходит до школьника, согласно условию, спустя время и школьник слышит максимум громкости.

За время t самолёт успевает удалиться от точки максимального сближения со школьником в направлении перпендикулярном L на расстояние, равное Таким образом, и скорость самолета

Источник

10 класс

§ 5. Равномерное прямолинейное движение

Равномерное прямолинейное движение. Скорость.

Если нам известно, что автомобиль в данный момент времени находится в определённом месте на шоссе, то мы ещё ничего не знаем о том, как он движется. Важной физической величиной, характеризующей движение тела, является его скорость. Со скоростью вы знакомы из повседневной жизни. Скорость показывает, как быстро движется тело, т. е. как быстро с течением времени меняется его положение в пространстве по отношению к другим телам.

Самое простое движение — это равномерное движение тела по прямой. Для этого движения проще всего определить, что такое скорость.

Движение тела называют равномерным прямолинейным, если его траектория представляет собой прямую линию и тело за любые равные промежутки времени проходит равные расстояния.

При равномерном прямолинейном движении координаты движущегося тела изменяются одинаково за любые равные промежутки времени.

Скоростью равномерного прямолинейного движения называют отношение изменения координаты тела Δx к промежутку времени Δt, за который это изменение координаты произошло.

Обратим внимание, что здесь речь идёт о проекции скорости движения тела на координатную ось X. Если обозначить скорость через υ_x, то, согласно определению:

В СИ единица скорости — метр в секунду (м/с).

Если скорость движения тела постоянна, то координата меняется со временем по простому закону. В § 4 «Перемещение. Радиус-вектор»мы рассмотрели векторный способ представления таких кинематических характеристик движения, как радиус-вектор, вектор перемещения. Прямолинейное движение тела также можно описывать с помощью векторов. Однако заметных преимуществ для данного вида движения это не даёт, поэтому в этом параграфе мы будем использовать координатный способ описания движения.

Рассмотрим движение тела, начиная с момента времени t₀ = 0. Пусть в начальный момент времени координата тела равна x₀ (рис. 2.10).

Отсюда следует, что

Выражение (2) называют кинематическим уравнением равномерного прямолинейного движения.

Видно, что зависимость координаты тела от времени является линейной функцией времени. Так как проекция скорости υ_х тела на координатную ось X может быть как больше, так и меньше нуля, то координата х или возрастает, или убывает. Итак, для определения координаты тела в произвольный момент времени необходимо знать начальную координату x₀ и скорость υ_х.

Подчеркнём, что формула (2) непосредственно определяет координату движущегося тела, но не пройденный путь.

Длину отрезка траектории, пройденного телом за некоторый промежуток времени, называют путём, пройденным за этот промежуток времени.

При прямолинейном движении в одном направлении пройденный путь s (см. рис. 2.10) равен модулю изменения координаты:

Зная модуль скорости движения тела, можно найти пройденный им путь:

Из выражения (3) следует, что модуль скорости υ равен

Отметим, что при криволинейном движении модуль перемещения не равен пути, пройденному телом с момента времени t₁ до момента времени t₂ (рис. 2.11), т. е. длина кривой A₁A₂ больше длины вектора перемещения.

Графическое представление равномерного прямолинейного движения.

При равномерном прямолинейном движении проекция скорости тела υ_х = const. Поэтому и её модуль υ = const (т. е. не изменяется с течением времени). Графиком зависимости модуля скорости υ от времени t является прямая АВ, параллельная оси времени и расположенная выше этой оси, так как υ > 0 (рис. 2.12, a).

Обратите внимание на то, что по графику зависимости x(t) можно находить положения тела до начала отсчёта времени при условии, что и до этого момента оно двигалось равномерно и прямолинейно с той же скоростью. Моменты времени до начала отсчёта считают отрицательными. Согласно рисунку 2.14, за 3 с до начала отсчёта времени координата тела была равна 4,5 м.

Таким образом, все графики равномерного прямолинейного движения представляют собой прямые линии. Для их построения достаточно указать значения х или s для двух моментов времени.

Вопросы:

1. Какое движение тела называют равномерным прямолинейным?

2. Как можно определить скорость равномерного прямолинейного движения?

3. Что представляет собой кинематическое уравнение равномерного прямолинейного движения?

4. Почему путь не может быть отрицательной величиной?

5. Какую информацию можно получить, анализируя графики равномерного прямолинейного движения?

Вопросы для обсуждения:

2. Опишите характер движения пешехода, используя рисунок 2.15.

3. Какой физический смысл имеет угол наклона графика зависимости координаты от времени к оси времени при равномерном прямолинейном движении?

Пример решения задачи

По графикам зависимости координат тел 1 и 2 от времени (рис. 2.16) для каждого тела определите проекцию скорости на ось X. Запишите кинематические уравнения движения этих тел. Для каждого из них постройте графики зависимости проекции скорости от времени.

Решение:

Начальная координата обоих тел x₀ = 0, поэтому кинематическое уравнение движения для каждого тела можно записать в виде:

Проекцию скорости движения можно найти по графику как отношение изменения координаты к промежутку времени, за который это изменение произошло:

Учитывая полученные данные, построим графики зависимости υ_х(t) для каждого тела (рис. 2.17).

Упражнения

2. От станции А по направлению к станции В отправился товарный поезд со скоростью 30 км/ч. Через 0,5 ч от станции в том же направлении вышел пассажирский поезд. C какой по модулю скоростью должен двигаться пассажирский поезд, чтобы догнать товарный поезд на станции В? Расстояние между станциями составляет 45 км.

3. Навстречу друг другу движутся пассажирский поезд со скоростью 90 км/ч и скорый поезд со скоростью 120 км/ч. Расстояние между поездами равно 70 км. На каком расстоянии от скорого поезда должен находиться разъезд, чтобы поезда разошлись без остановки?

4. Два мотоцикла движутся прямолинейно и равномерно. Скорость движения первого мотоцикла по модулю больше скорости движения второго мотоцикла. Постройте для данных тел графики зависимости:

б) модуля скорости от времени.

а) начальную координату тела;

б) проекцию и модуль скорости его движения;

Источник

Уравнение координаты при равноускоренном прямолинейном движении

теория по физике 🧲 кинематика

Уравнение координаты — зависимость координаты тела от времени:

Уравнение координаты при равноускоренном прямолинейном движении:

x₀ — координата тела в начальный момент времени, v_0x —проекция начальной скорости на ось ОХ, a_x —проекция ускорения на ось ОХ, x — координата тела в момент времени t

Зная уравнение координаты, можно определить координату тела в любой момент времени.

Пример №1. Движение автомобиля задано уравнением:

Определить начальное положение автомобиля относительно тела отсчета, его начальную скорость и ускорение. Также найти положение тела относительно тела отсчета в момент времени t = 10 c.

В момент времени t = 10 c координата автомобиля равна:

Совместное движение двух тел

Иногда в одной системе отсчета рассматривается движение сразу двух тел. В этом случае движение каждого тела задается своим уравнением. Эти уравнения используются для нахождения различных параметров движения этих тел. Такой способ решения задач называется аналитическим.

Аналитический способ решения задачи на совместное движение тел

Чтобы найти место встречи двух тел, нужно:

Пример №2. По одному направлению из одной точки начали двигаться два тела. Первое тело движется прямолинейно и равномерно со скоростью 3 м/с. Второе тело — равноускорено с ускорением 1 м/с 2 без начальной скорости. Определите, через какое время второе тело догонит первое. Вычислите, на каком расстоянии от тела отсчета это произойдет.

Составим уравнения для движения каждого из тел:

Приравняем правые части этих уравнений и найдем время t:

Отсюда t₁ = 0 с, а t₂ = 6 с. Первый корень нам не подходит — из условия задачи уже было понятно, что тела начали движение одновременно. Снова они встрется, когда пройдет 6 секунд.

Чтобы найти, какое расстояние они пройдут за это время, подставим известное время в любое из уравнений:

Графический способ решения задачи на совместное движение тел

Существует графический способ решения данной задачи. Для этого нужно:

Таким способом можно определить, в какое время произойдет встреча двух тел. Нужно лишь провести перпендикуляр к оси времени после построения графиков перемещений.

Графический способ решения задач требует высокой точности построения графиков. Поэтому он применяется редко!

Если в одной системе описывается движение двух тел, и одно тело начинает движение с опозданием t_запазд, то его уравнение координаты принимает вид:

Если Саша догонит Мишу до того, как мальчики станут двигаться с равномерной скоростью, уравнение движения с равномерной скоростью можно игнорировать. Если это так, то корнем уравнения будет время, не превышающее 4 с (через столько времени оба мальчика начнут двигаться равномерно).

В таком случае составим уравнения только для тех участков пути, на которых мальчики двигались равноускорено:

Приравняем правые части уравнений и вычислим t:

В результате получаем два корня: t₁ = 0,6 с, а t₂ = 3,4 с. Первый корень не подходит, так как в это время Саша еще не начал движение. Второй корень подходит, так как он меньше 4 с. Значит, Саша догонит Мишу через 3,4 с после того, как Миша начнет движение.

Материальная точка движется прямолинейно с постоянным ускорением. График зависимости её координаты от времени x=x(t) изображён на рисунке.

В момент времени t=0 проекции её скорости υ_x и ускорения a_x на ось Ох удовлетворяют соотношениям:

а)

б)

в)

г)

pазбирался: Алиса Никитина | обсудить разбор | оценить

Алгоритм решения

Решение

Запишем уравнение движения грузовика:

Так как начальная координата равна нулю, это уравнение примет вид:

Отсюда скорость движения грузовика равна:

Запишем уравнение движения мотоциклиста:

Так как начальная координата равна нулю, начальная скорость тоже нулевая, и мотоциклист начал движение позже грузовика, это уравнение примет вид:

Найдем время, через которое грузовик и мотоциклист встретились:

Подставим найденное время встречи в формулу для вычисления проекции скорости грузовика:

pазбирался: Алиса Никитина | обсудить разбор | оценить

Источник