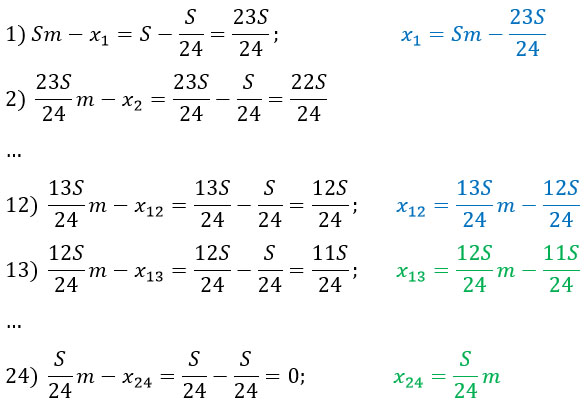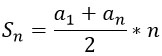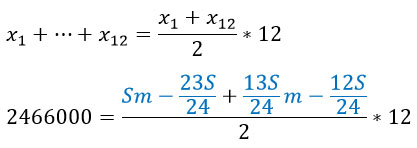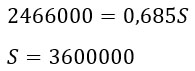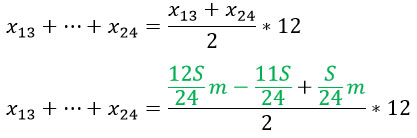Известно что в течение первого года кредитования нужно вернуть банку 2466 тыс
Если видишь в условии задачи фразу “на одну и ту же”, то это задача на дифференцированный платеж. О разнице аннуитетного и дифференцированного платежах можно посмотреть здесь на примерах двух задач.
m = 1 + 2/100 = 1,02 (полезный коэффициент; увеличитель суммы долга)
Если долг на одну и ту же величину меньше, то это говорит о том, что он уменьшается равномерно каждый месяц на S/24 (всю сумму кредита S разделили на 24 месяца).
Помимо этого мы знаем, что каждый месяц долг увеличивается на 2% (в m раз) и делается выплата.
Помимо того, что я распишу изменение суммы долга, я сразу выражу выплаты, которые должны будут производиться.
Как мы уже знаем, долг уменьшается равномерно на одну и ту же сумму, т.е. уменьшается в арифметической прогрессии.
Выразим сумму выплат за первые 12 месяцев по формуле суммы первых n членов арифметической прогрессии. Сама формула выглядит так:
Адаптируя ее под нашу задачу, получим вот что:
Путем несложных преобразований найдем S.
Теперь выразим сумму выплат за последние 12 месяцев.
Преобразуем правую часть уравнения и подставим найденную S:
Ответ: 2034000 рублей.
Не можешь найти нужную задачу? Предложи свою! Наша группа в VK.
Известно что в течение первого года кредитования нужно вернуть банку 2466 тыс
Источник задания: Решение 3752. ЕГЭ 2016 Математика, И.В. Ященко. 36 вариантов. Ответ.
Задание 17. 15 января планируется взять кредит в банке на 24 месяца. Условия его возврата таковы:
– 1-го числа каждого месяца долг возрастает на 2% по сравнению с концом предыдущего месяца;
– со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
– 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца.
Известно, что в течение второго года кредитования нужно вернуть банку 339 тыс. рублей. Какую сумму нужно вернуть банку в течение первого года кредитования?
Обозначим через 
размер кредита, взятого в банке. Во втором месяце долг увеличивается на 2% и, затем, осуществляется выплата так, чтобы долг уменьшался на одну и ту же величину, т.е. в первый раз выплата будет составлять 
, и сумма долга во втором месяце составит
.
Аналогично для следующего месяца, только долг теперь будет составлять 
, получаем остаток долга в размере
.
После 24 месяцев выплаты будут составлять сумму, равную
.
Из этого выражения выделим слагаемые, отвечающие за выплаты во втором году:
и перепишем это выражение в виде
По условию задачи, выплаты составили 339 тыс. рублей, получаем уравнение
То есть сумма кредита составила 600 тыс. рублей. Таким образом, в первый год кредитования было выплачено
Подставим вместо 
, получим:
тыс. рублей.
Известно что в течение первого года кредитования нужно вернуть банку 2466 тыс
Источник задания: Решение 2852. ЕГЭ 2016 Математика, И.В. Ященко. 30 вариантов. Ответ.
Задание 17. 15-го января планируется взять кредит в банке на 24 месяца. Условия его возврата таковы:
— 1-го числа каждого месяца долг возрастает на 3% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца.
Известно, что в течение первого года (первых 12 месяцев) кредитования нужно вернуть банку 1399,5 тыс. рублей. Какую сумму планируется взять в кредит?
Обозначим через 
тыс. рублей сумму кредита. Тогда 1-го числа первого месяца данная сумма увеличится на 3% и станет равной 
. Выплату нужно сделать так, чтобы сумма долга равномерно уменьшалась каждый месяц. Учитывая, что кредит взят на 24 месяца, сумма долга после первого месяца должна быть равна 
, т.е. платеж будет равен
.
Во второй месяц, долг также увеличивается 
и сумма платежа должна составить
,
то есть долг будет равен 
.
Соответственно, на 12-й месяц сумма платежа будет равна:
и сумма всех платежей за первые 12 месяцев составят
В задаче сказано, что величина 
равна 1399,5 тыс. рублей, получаем уравнение:
,
тыс. рублей
то есть в банке был взят кредит в размере 1800000 рублей.
Известно что в течение первого года кредитования нужно вернуть банку 2466 тыс
Источник задания: Решение 2752. ЕГЭ 2016 Математика, И.В. Ященко. 30 вариантов. Ответ.
Задание 17. 15-го января планируется взять кредит в банке на 24 месяца. Условия его возврата таковы:
— 1-го числа каждого месяца долг возрастает на 1% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца.
Известно, что в течение второго года (последних 12 месяцев) кредитования нужно вернуть банку 798,75 тыс. рублей. Какую сумму нужно вернуть банку в течение первого года (последних 12 месяцев) кредитования?
Обозначим через 
тыс. рублей сумму кредита, взятого в банке. После 1-го числа начисляется 1%, т.е. сумма долга становится равной 
. Затем, нужно сделать платеж так, чтобы сумма долга равномерно уменьшалась каждый месяц на одну и ту же величину, т.е. после первого месяца она должна составить 
, и, следовательно, величина выплаты равна
.
1-го числа следующего месяца сумма вновь увеличивается на 1%: 
, а, затем, осуществляется платеж такой, чтобы сумма долга равнялась 
, получаем:
.
На 24-й месяц (последний) нужно сделать платеж в размере:
.
Таким образом, сумма выплат за последние 12 месяцев составит:
,
По условию задачи величина 
равна 798,75, находим сумму кредита:
.
Теперь, зная сумму кредита, найдем сумму выплат за первые 12 месяцев, имеем:
Известно что в течение первого года кредитования нужно вернуть банку 2466 тыс
Источник задания: Решение 5052. ЕГЭ 2016 Математика, И.В. Ященко. 36 вариантов. Ответ.
Задание 17. 15 января планируется взять кредит в банке на 24 месяца. Условия его возврата таковы:
– 1-го числа каждого месяца долг возрастает на 2% по сравнению с концом предыдущего месяца;
– со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
– 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца.
Известно, что в течение первого года кредитования нужно вернуть банку 822 тыс. рублей. Какую сумму нужно вернуть банку в течение второго года кредитования?
Пусть 
размер кредита, взятого в банке. После первого месяца начисляются 2%, что составляет 
и нужно сократить долг так, чтобы он уменьшался пропорциональными частями каждый месяц, т.е. нужно выплатить в первый месяц 
, получим сумму долга на второй месяц
.
Аналогично для второй выплаты, сумма выплачиваемого долга должна составлять 
и тогда сумма долга будет равна
.
В результате, сумма выплат за первый год составят:
По условию задачи сумма выплаченного долга за первый год составила 822 тыс. рублей, получаем уравнение
То есть сумма кредита составляет 1200 тыс. рублей. Вычислим сумму долга, возвращаемую во второй год кредитования, имеем:
перепишем выражение в виде
Подставим вместо сумму кредита, получим:
тыс. рублей.