как гадать японские кроссворды с цифрами на поле

Как разгадывать японские кроссворды

13 Мар 2016г | Раздел: Разное

Здравствуйте, уважаемые читатели сайта sesaga.ru. Японские кроссворды от обычных отличаются тем, что для их решения не требуется ломать голову, чтобы отгадывать разнообразные замысловатые слова. В японском кроссворде зашифрована картинка, которую необходимо разгадать путем закрашивания клеток.

Кроссворд представляет собой поле, состоящее из определенного количества пустых клеток, которые в процессе разгадывания закрашивают в нужной последовательности, указанной цифрами подсказками.

Цифры-подсказки указывают на количество закрашенных клеток в вертикальных и горизонтальных линиях кроссворда, и при этом каждая цифра образует группу из слитно закрашенных клеток, между которыми оставляют пропуск в одну или несколько пустых клеток.

Для удобства счета клетки объединяют в квадраты по 5 клеток, а сами квадраты выделяют толстыми линиями, что позволяет производить пересчет сразу по пять клеток.

Группы клеток закрашивают в той последовательности, в какой расположены цифры-подсказки: для горизонтальной линии отсчет начинают от левой границы поля, а для вертикальной линии от верхней границы. Но при этом необходимо учитывать, что в зависимости от рисунка между первой клеткой группы и границей поля может быть несколько пустых клеток.

Разгадывать кроссворд начинают с поиска самых больших цифр-подсказок, находящихся в вертикальных и горизонтальных линиях, потому как именно эти цифры с большим количеством слитных клеток закрашивают первыми, а затем от этих закрашенных клеток отталкиваются при дальнейшем решении кроссворда.

При разгадывании японских кроссвордов усвойте несколько правил:

1. Используйте простой карандаш, так как это дает шанс в случае ошибки стереть неправильное решение и продолжить разгадывать кроссворд. В случае ошибки рекомендую не тратить время на поиск ошибки, а очистить поле полностью и приступить к решению кроссворда сначала.

2. В процессе решения кроссворда необходимо отмечать пустые клетки, в которых не может быть рисунка. Это уменьшает площадь поиска и облегчает разгадывания рисунка.
Как правило, пустые клетки зачеркивают крестиком или отмечают точкой. Если отмечать точками, то рисунок получается более выразительным.

3. Каждая найденная группа закрашенных клеток, отделяется с двух сторон точкой или крестиком. Допустим, что мы определили группу из пяти клеток в горизонтальной линии 5, 3, 1. Значит, перед первой и после последней клеточкой ставим точку.

Когда в горизонтальной линии будут найдены все группы клеток 5, 3, 1, то каждая отделяется с обеих сторон.

Ну и теперь, когда в горизонтальной линии 5, 3, 1 окончательно найдены все три группы клеток, но еще остались пустые клеточки, то эти пустые клеточки заполняем точками, так как в этой линии больше никаких закрашенных клеток быть не должно.

Таким же образом поступаем и с вертикальной линией.

4. Цифры-подсказки, линии которых будут полностью заполнены точками и группами, желательно зачеркнуть. Зачеркнутая цифра будет указывать, что линия закончена и на эту цифру больше не стоит обращать внимания.

5. В японском кроссворде нет приблизительных решений — только точный расчет. Нельзя приблизительно закрасить клетку или выделить пустую.

Сам процесс разгадывания японского кроссворда описать очень сложно, потому как при его решении возникает много «если», которые в рамках одной страницы не объяснить. Взять хотя бы одну клеточку, при закрашивании которой может возникнуть несколько вариантов с «если».

Предлагаю Вам посмотреть видеоролики, где в процессе решения кроссвордов я постарался рассказать основные моменты, возможные нюансы и маленькие хитрости. В первом ролике разгадывается легкий кроссворд, рассчитанный на начинающих, а во втором разгадывается сложный, но объяснение дается также, с расчетом на начинающих.

Также можете почитать статью и посмотреть ролик как решать судоку.
Удачи!

Источник

Как решать японские кроссворды?

Японский кроссворд (по-другому нонограмма) — это головоломка, в которой, в отличие от обычных кроссвордов, зашифрованы не слова, а изображения.

Подобные нонограммы появилась в Японии в конце XX века и, несмотря на непривычный вид и пугающую на первый взгляд трудность, смогли завоевать популярность у любителей головоломок во всем мире, в том числе и в России.

Правильно разгадать японский кроссворд – значит, восстановить изображение, зашифрованное с помощью цифр. Шифрованным изображением может быть любой объект: транспорт, животное, человек, любые символы. Профессионально составленный кроссворд должен иметь единственное логическое решение без каких-либо вариантов.

Научиться разгадывать японские кроссворды несложно. Для этого достаточно усвоить алгоритм решения нонограммы на достаточно простом примере, чтобы понять всю суть данной головоломки, а затем можно смело выбирать кроссворды со сложными изображениями.

Поскольку правила решения цветных и чёрно-белых кроссвордов несколько различаются, рассмотрим, прежде всего, особенности составления и решения чёрно-белых кроссвордов.

Для начала обратим внимание на схему подобного кроссворда.

пример разгаданного японского кроссворда

Как видим, поле японского кроссворда расчерчено горизонтальными и вертикальными линиями разной толщины. Самые толстые линии отделяют поле для картинки от цифр. Более тонкими линиями поле делится на группы по 5 клеток (как по горизонтали, так и по вертикали) исключительно для удобства подсчёта.

Само изображение в японском кроссворде формируется путем закрашивания отдельных клеток в чёрный цвет. Не закрашенная клетка при этом считается белой. В процессе решения необходимо восстановить картинку по имеющимся цифрам.

Таким образом, цифры в сетке японского кроссворда слева и сверху означают количество заштрихованных клеток, идущих подряд, без пропусков, по горизонтали и вертикали соответственно. Каждая отдельная цифра обозначает отдельную группу. Например, набор чисел 7, 1 и 2 в сетке японского кроссворда означает, что в этом ряду есть три группы: первая — из семи, вторая — из одной, третья — из двух чёрных клеток. Причём между группами должна быть как минимум одна не закрашенная клетка. Пустые клетки могут быть и по краям рядов. При решении японского кроссворда необходимо определить размещение этих групп клеток.

Начинать разгадывание рекомендуется с нахождения горизонтальных линий или вертикальных столбцов, где можно сделать какой-либо вывод о том, какие клетки закрашены, а какие не закрашены. Эти логические выводы можно отображать специальными пометками, которые помогут получить новые зацепки для разгадывания кроссворда.

ПРИМЕР РЕШЕНИЯ ЯПОНСКОГО КРОССВОРДА:

Рассмотрим простой пример, состоящий из 9 строк и 9 столбцов.

Заштрихованные клетки будем обозначать квадратом чёрного цвета, а пустое поле — синим крестиком. Для удобства числа после определения их местоположения будем вычёркивать.

Обратим внимание, что в результате первого шага, у нас автоматически нашлось решение для первой строки, а также для первого и девятого столбца, где во всех случаях быть закрашена всего одна клетка. А это значит, что все остальные клетки в этих рядах будут пустыми. Вычёркиваем все три использованные цифры и отмечаем пустые клетки.

Опять внимательно изучаем результат предыдущих действий. Становится ясно, что в четвёртой строке снова определяется вся группа из семи идущих подряд клеток, которые можно смело заштриховать.

Всегда следует обращать внимание на самые большие из предложенных чисел, которые легче дают зацепку для дальнейшего решения головоломки. В нашем случае это две шестёрки во втором и восьмом столбце. Поскольку место положения группы из шести клеток в данных комбинациях буден неоднозначным, попробуем рассуждать логически. Заодно познакомимся с одним из основных принципов решения японских кроссвордов. Запоминаем простое правило. Если число рядом со строкой или столбцом всего одно, и оно составляет больше половины длины, то можно закрашивать несколько клеток в середине. В нашем случае это центральные четыре клетки. Как не размещай в восьми клетках группу из шести клеток, четыре центральные обязательно окажутся закрашенными (т.е. 8-6=2, что означает количество “неизвестных” клеток сверху и снизу). Поскольку, окончательное решение по данным столбцам мы ещё не приняли, сами цифры пока не вычёркиваем, а обводим красным кружком. Сюда мы вернёмся позже, когда получим новую зацепку.

И снова нам улыбнулась удача. В шестой и седьмой строке решение обозначилось автоматически в результате предыдущих манипуляций. Вычёркиваем ненужные цифры и отмечаем пустые клетки.

Поскольку кроссворд довольно простой, уже просматривается несколько вариантов его дальнейшего решения. Они очевидны. Можно пойти любым путём. Например, снова обратить внимание на самые большие из оставшихся цифр. Пятёрку в третьей строке пока оставим в покое, т.к. проще сначала вычеркнуть цифру 4 в очевидном шестом столбце. Не забываем отмечать пустые клетки.

Теперь не оставляет сомнения местоположение группы из трёх клеток в соседнем столбце справа.

Обратим внимание на столбцы слева. В четвёртом столбце прорисовываем области из четырёх и двух сплошных клеток, место которых определилось однозначно.

И снова во второй строке мы видим, что вся группа из трёх клеток уже стоит на своём месте. Остаётся только зачеркнуть эту цифру.

Обратим внимание на третий столбец. Также очевидно, где находятся две группы из трёх и двух обозначенных клеток.

А вот и наша пятёрка в третьей строке нарисовалась сама собой. Остаётся только оформить пустые клетки по бокам.

Возвращаемся к нашим шестёркам во втором и восьмом столбце, решение которых мы отложили до лучших времён. Самое время дорисовать группу из шести клеток в обоих столбцах.

Логическим завершением головоломки будет оформление уже обозначившихся двух нижних строк. Перечёркиваем пустые клетки, и японский кроссворд решён. Картинка получена.

Источник

Как разгадывать японские кроссворды

Что такое японские кроссворды

Изображения в японском кроссворде зашифрованы с помощью чисел. Числа расположены слева и сверху от основного игрового поля. Числа показывают сколько ячеек надо закрасить.

Числа над игровым полем, показывают, сколько закрашенных ячеек должно быть в каждом столбце.

Числа слева от игрового поля, показывают сколько закрашенных ячеек должно быть в каждой строке.

Основные требования к японскому кроссворду:

Основные шаги для решения

При решении кроссворда вам необходимо:

Пример решения японского кроссворда

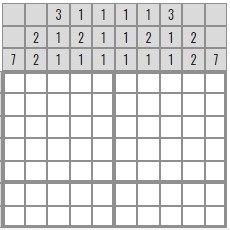
Давайте попробуем решить простой японский кроссворд «Письмо»:

Размер кроссворда 10 на 7. Давайте попробуем разгадать его.

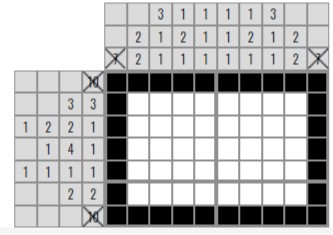
Для начала найдем все ячейки. В первой и последней строке есть число 10, значит вся строка будет закрашена полностью. Также в первом и последнем столбце есть число 7, значит весь столбец будет закрашен полностью. Давайте закрасим эти строки и столбцы и зачеркнем соответствующие числа.

Теперь внимательно посмотрим на вторую и 6 строку. У этих чисел есть начальные и конечные закрашенные ячейки. Соответственно, мы их можем продолжить или завершить.

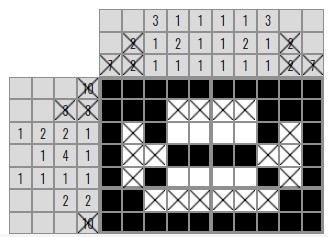
Теперь давайте отметим крестиками те ячейки, где точно не могут быть закрашены

Посмотрите на 3 и седьмую строки. Т.к. между закрашенными ячейками должна быть одна пустая ячейка и есть первые две закрашенные клетки, мы можем закрасить остальные

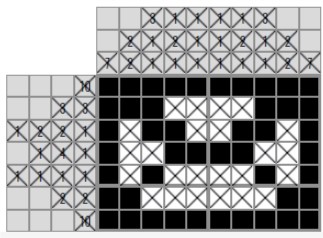
На 4 строке остается только место для числа 4. Давайте закрасим его.

На 3 строке есть начало и конец для чисел 2. Давайте закрасим их.

Поздравляю Вас! Вы успешно решили кроссворд и узнали азы разгадывания японских кроссвордов.

Теперь попробуйте еще раз разгадать этот кроссворд самостоятельно!

Источник

Как решать японские кроссворды

Японские кроссворды представляют собой головоломку, скрывающую изображение. Нонограммы появились в конце ХХ в. в Японии. Они отличаются размерами, сложностью, количеством цветов. Есть различия и в том, как решать японские кроссворды, в зависимости от размеров изображения и доступных цифр.

Основная информация про нонограммы

Нонограмма – это головоломка, в которой спрятано изображение. Различают 2 вида японских кроссвордов: черно-белые и цветные. Картинка в обоих случаях представлена в виде закрашенных и пустых клеток на поле.

На положение и количество зарисованных квадратов в каждом ряду указывают цифры над верхней и левой границами.

Решить японский кроссворд означает восстановить изначальный вид рисунка, т.е. найти верное расположение всех зарисованных квадратов на поле и закрасить их нужным цветом.

Основные элементы японских кроссвордов:

Требования к кроссворду:

За счет однозначности правил, можно найти решение всех японских кроссвордов. Главное быть внимательным и выбрать правильную тактику.

Главные правила решения

Пошаговой инструкции, которая объясняет, как разгадывать японские кроссворды, и подходит для всех случаев, нет. Каждая картинка требует индивидуального подхода, но есть несколько основных шагов. Задача перед решающим сводится к определению максимального количества закрашенных и незакрашенных ячеек в каждом ряду.

Начинать следует с поиска наибольших чисел, двигаясь по убыванию.

Для проверки клеток на закрашенность используют несколько методов. Они применимы к кроссвордам любой величины и сложности.

Освоив основные методы, новичок научится решать простые японские кроссворды.

Чтобы не запутаться, о каких квадратах идет речь, в описании методов используются 3 слова:

Цифры, которые обозначают уже закрашенные блоки, зачеркивают для удобства.

Отталкивание от границы

Если в строке или столбце первый зарисованный квадрат находится на меньшем расстоянии от границ поля, чем подходящая для него цифра, можно закрасить еще несколько ячеек дальше от него. Количество закрашиваемых квадратов равняется разности между положением уже зарисованного квадрата и первым числом. Работает это для правой и нижней границы, сравнению подлежат последние числа по столбику и по строке.

Например, если первая цифра в строке 5, а на этой линии закрашена 4 клетка, можно закрасить еще 1 после нее – при любом раскладе она будет закрашена.

Так отталкиваются не только от границ поля, но и от клеток с крестиком. Метод применим для второй и следующих цифр в ряду.

Наложение крайних позиций

Если рядом со строкой или столбцом записано одно число, которое больше половины ряда, закрашивают несколько квадратов в середине.

Для этого нужно наложить крайнее левое положение блока на крайнее правое – место, где они пересекаются, точно будет закрашено. Отталкиваться при использовании этого метода можно и от квадратов, помеченных крестиком.

Этим приемом можно пользоваться, если блок не один. Тогда накладывается крайнее левое положение всей группы на крайнее правое, при этом отступ между блоками в группе должен быть минимальным. Закрашивать можно только те клетки, в которых блоки наложились сами на себя.

Разделение имеющихся полос

Если на поле есть 2 полосы и между ними 1 пустая клетка, то нужно проверить, можно ли ее закрасить. Если при зарисовке получается полоса больше, чем допустимая условием в этом ряду, то она точно не будет закрашенной и ее сразу можно отметить крестиком. Часто после такого разделения полосы по обе стороны от крестика можно достроить и вычеркнуть несколько чисел из условия.

Например, если в ряду есть только цифры 1 и 2, то три ячейки подряд закрашены быть точно не могут. Значит посередине будет пустая клетка.

Если между полосами есть пробел и вы точно уверены, что обе полосы – это часть одного блока, то пропуск между ними нужно закрасить. Например, в ряду нужно разместить блоки 1, 6, 2 и есть 2 закрашенных полосы по 2 и 3 квадрата. Обе полоски не могут быть частями блоков 1 и 2, а значит, пропуск между ними точно можно закрасить – это части элемента из 6 квадратов.

Проверка пустых клеток

Бывают ситуации, когда закрашенные полосы могут подсказать, какие квадраты на поле точно будут пустыми. Если ни одно из возможных положений блока, соответствующего этой полосе, не затрагивает какие-то ячейки поля, в них ставится крестик.

Например, в строчке из 10 квадратов зарисованы 2 в середине, а в ряду должно быть закрашено 5 подряд. Тогда любое положение 5 клеток не задевает 1 крайний квадрат справа и 1 слева. Их можно зачеркнуть.

Случается и так, что в ограниченную 2 или больше крестиками область не помещается ни в один блок из этого ряда. Тогда пустые квадраты тоже заполняются крестиками.

Взаимоисключающие позиции

Если любое положение группы блоков исключает возможность закрашивания некоторой клетки, ее отмечают крестиком.

Например, в ряду, состоящем из 13 ячеек, нужно разместить 2 блока по 4 и 3 квадрата, при этом 3 квадрата в центре уже зарисованы, а в 5 нарисован крестик. Если закрашенная полоска относится к блоку из 3 квадратов, то оставшиеся справа ячейки будут пустыми. Если к блоку из 4, то 10-й квадрат будет пустым. В обоих вариантах 10-й квадрат отмечается крестиком.

Отличается ли решение цветных кроссвордов

Главная отличительная черта цветных японских кроссвордов – это наличие 3 и более цветов. Методы заполнения у них остаются прежними.

Дополнительную сложность представляет соответствие цветов в столбцах и строках. Если при решении черно-белой нонограммы не нужно сверять положение каждого квадрата по столбикам и строкам, то при цветной такая необходимость есть. Важно не только правильно определить положение закрашенных клеток, но и не перепутать цвет.

Кроме того, немного отличается поле головоломки: фон у цифр совпадает с цветом закрашенной полосы на поле.

Правила про обязательный отступ между блоками одинакового цвета сохраняется, но между блоками разных цветов пропуска может не быть. В остальном построение кроссвордов идентично.

Проверка цветов на пересечении

Важная особенность цветных кроссвордов – цветовое соответствие. Если выбрана возможная клетка для цвета по горизонтали, в этом ряду по вертикали должен присутствовать такой же цвет, иначе зарисовать квадрат нельзя.

Такая особенность позволяет откинуть множество вариантов расположения цветных блоков и упрощает решение головоломки.

Как и во многих других логических играх, научиться разгадывать японские кроссворды можно только опытным путем. Чем больше вы будете тренироваться, тем быстрее сможете перейти от самых простых загадок к профессиональным.

Источник

Решение цветных японских кроссвордов со скоростью света

Японские кроссворды (также нонограммы) — логические головоломки, в которых зашифровано пиксельное изображение. Разгадывать кроссворд нужно с помощью чисел, расположенных слева от строк и сверху от столбцов.

Размер кроссвордов может доходить до 150×150. Игрок с помощью специальных логических приемов вычисляет цвет каждой клетки. Решение может занять как пару минут на кроссвордах для начинающих, так и десятки часов на сложных головоломках.

Хороший алгоритм может решить задачу намного быстрее. В тексте описано, как с помощью наиболее подходящих алгоритмов (которые вообще приводят к решению), а также их оптимизаций и использования особенностей C++ (которые уменьшают время работы в несколько десятков раз) написать решение, работающее почти мгновенно.

В мобильной версии Хабра формулы в тексте могут не показываться (не во всех мобильных браузерах) — пользуйтесь полной версией или другим мобильным браузером, если заметили проблемы с формулами

Правила игры

Изначально холст кроссворда белый. Для ванильных черно-белых кроссвордов нужно восстановить местоположения черных клеток.

В черно-белых кроссвордах количество чисел для каждой строки (слева от холста) или для каждого столбца (сверху от холста) показывает, сколько групп черных клеток находятся в соответствующих строке или столбце, а сами числа — сколько слитных клеток содержит каждая из этих групп. Набор чисел значит, что в определенном ряду есть три последовательные группы из , и черных клеток подряд. Группы могут быть расположены в ряду как попало, не нарушая относительный порядок (цифры задают их длину, а позицию надо угадать), но они обязательно должны разделяться хотя бы одной белой клеткой.

В цветных кроссвордах у каждой группы еще есть свой цвет — любой, кроме белого, это фоновый цвет. Соседние группы разных цветов могут стоять вплотную, но для соседних групп одинаковых цветов разделение хотя бы одной белой клеткой еще обязательно.

Что не является японским кроссвордом

Каждое пиксельное изображение можно зашифровать в виде кроссворда. Но восстановить обратно может быть невозможно — получившаяся головоломка может либо иметь более одного решения, либо иметь одно решение, но не может быть решена логическим путем. Тогда оставшиеся клетки в процессе игры приходится отгадывать, используя квантовые компьютеры шаманские технологии.

Такие кроссворды являются не кроссвордами, а графоманией. Считается, что корректный кроссворд — такой, что логическим путем можно прийти к единственному решению.

“Логический путь” — это возможность восстановить каждую клетку одну за другой, рассматривая строку/столбец по отдельности, или их пересечение. Если такой возможности нет, количество рассматриваемых вариантов ответа может быть очень много, намного больше, чем человек сможет посчитать сам.

Неправильная нонограмма — решение единственное, но решить нормально нельзя. Оранжевым помечены “нерешаемые” клетки. Взято из Wikipedia.

Такое ограничение объясняется так — в самом общем случае японский кроссворд это NP-полная задача. Однако, NP-полной задачей разгадывание не становится, если есть алгоритм, в каждый момент времени однозначно указывающий, какие клетки открыть далее. Все методы разгадывания кроссвордов, применяемые человеком (за исключением метода Монте-Карло проб и ошибок), основываются именно на этом.

У наиболее православных кроссвордов ширина и высота делится на 5, нет рядов, которых можно посчитать мгновенно (такие, где либо цветные клетки забивают все места, либо их нет совсем), и ограничено количество дополнительных цветов. Эти требования не обязательные.

Наипростейший неправильный кроссворд:

Часто не решаются взад закодированные пиксельные арты, в которых используется “шахматный порядок” для имитации градиента. Лучше понять будет, если вы наберете в поиске “pixelart gradient”. Градиент как раз похож на этот фейловый кроссворд 2×2.

Возможные варианты решений

У нас есть размер кроссворда, описание цветов и всех строк и столбцов. Как можно собрать из этого картинку:

Полный перебор

Для каждой клетки перебираем все возможные состояния и проверяем на удовлетворительность. Сложность такого решения для черно-белого кроссворда , для цветного . По аналогии с клоунской сортировкой это решение можно тоже назвать клоунским. Оно годится для размера 5×5.

Backtracking

Перебираются все возможные методы расстановки горизонтальных групп клеток. Ставим группу клеток в строке, проверяем, что она не ломает описание групп столбцов. Если ломает — ставим дальше на 1 клетку, опять проверяем. Поставили — переходим к следующей группе. Если группу поставить нельзя никак — откатываем две группы, переставляем предыдущую группу, и так далее, пока не поставим последнюю группу успешно.

Отдельно для каждого ряда

Это решение намного лучше и оно истинно верное. Мы можем проанализировать каждую строку и каждый столбец по отдельности. У каждого ряда попытаемся раскрыть максимум информации.

Алгоритм для каждой клетки в ряду узнает больше информации — может оказаться, что в какой-то цвет клетку окрасить невозможно, группы не сойдутся. Сразу строку полностью раскрыть нельзя, но полученная информация “поможет” раскрыться лучше нескольким столбцам, а когда мы начнем их анализировать, те опять “помогут” строкам, и так в течение нескольких итераций, пока для всех клеток не останется один возможный цвет.

Истинно верное решение

Одна строка, два цвета

Эффективное отгадывание черно-белого “однострочника”, для которого некоторые клетки уже отгаданы — весьма жесткая задача. Она встречалась в таких местах, как:

Монохромный однострочник тоже можно решать по-разному, и за (перебор всех вариантов, проверка на корректность, выделение клеток, которые имеют один и тот же цвет во всех вариантах), и еще как-то менее тупо.

Основная идея в том, чтобы использовать аналог бэктрекинга, но без лишних вычислений. Если мы как-то поставили несколько групп и сейчас находимся в какой-то клетке, то требуется узнать, можно ли поставить оставшиеся группы, начиная с текущей клетки.

Такой подход называется динамическим программированием. Псевдокод упрощен, и там даже запоминание вычисленных значений не производится.

Функции CanInsertBlack/CanInsertWhite нужны, чтобы проверить, можно ли теоретически поставить группу нужного размера в нужное место. Все что им надо сделать — проверить, что в указанном интервале клеток нет “100% белой” клетки (для первой функции) или “100% черной” (для второй). Значит, они могут работать за , это можно сделать с помощью частичных сумм:

Такое же колдунство с частичными суммами ждет строки вида

Тут можно вместо = True увеличивать число на 1. А если нам надо произвести много прибавлений на отрезке в неком массиве , и притом этот массив мы никак не используем перед разными прибавлениями (про такое говорят, что эта задача “решается оффлайн”), то вместо цикла:

Таким образом, работает весь алгоритм за , где — количество групп черных клеток, — длина строки. И мы проходим на полуфинал ACM ICPC или получаем бронзу межнара. Решение ACM (Java). Решение IOI (C++).

Одна строка, много цветов

При переходе на многоцветные нонограммы, которых еще непонятно, как решать, мы узнаем страшную правду — оказывается, на каждую строку магическим образом влияют все столбцы! Это понятнее через пример:

В то время как двухцветные нонограммы нормально обходились без этого, им не надо было оглядываться на ортогональных друзей.
На картинке видно, что у левого примера три крайние правые клетки пустые, потому что поломается конфигурация, если окрасить эти клетки в те цвета, в которых окрасить себя не-белый цвет.

Но этот прикол математически разрешим — надо каждой клетке выдать число, где -й бит будет означать, можно ли дать этой клетке -й цвет. Изначально у всех клеток значение . Решение динамики поменяется не очень сильно.

Можно будет наблюдать следующий эффект: в этом же левом примере, по версии строк, крайняя справа клетка может иметь либо синий либо белый цвет.
По версии столбцов, эта клетка имеет либо зеленый, либо белый цвет.
По версии здравого смысла, эта клетка будет иметь только белый цвет. И дальше мы продолжаем вычислять ответ.

Если считать нулевой бит “белым”, первый “синим”, второй “зеленый”, то строка вычислила для последней клетки состояние , а столбец . Значит, реально у этой клетки состояние

Много строк, много цветов

Постоянно делаем обновление состояний всех строк и столбцов, описанное в прошлом пункте, пока не останется ни одной клетки с больше чем одним битом. В каждой итерации после обновления всех строк и столбцов, обновляем состояния всех клеток в них через взаимный AND.

Первые результаты

Допустим, что код мы писали не как дятлы, то есть никуда по ошибке объекты не копируем вместо передачи по ссылке, нигде в алгоритме не косячим, велосипедов не изобретаем, для битовых операций используем __builtin_popcount и __builtin_ctz (особенности gcc), все аккуратно и чисто.

Посмотрим на время работы программы, которая считывает из файла головоломку и решает ее полностью. Стоит оценить достоинства машинки, на которой все это добро писалось и тестировалась:

Понятно, что такой суперкомпьютер был выбран, потому что оптимизации на нем имеют больший эффект, чем на летающей шайтан-машине.

Итак, после прогона нашего алгоритма на самом сложном кроссворде (по версии nonograms.ru), получаем не очень хороший результат — от 47 до 60 секунд (в это входит считывание из файла и решение). Надо заметить, что “сложность” на сайте посчитана хорошо — этот же кроссворд во всех версиях программы так же был самым тяжелым, другие наиболее сложные кроссворды по мнению архива держались в топе по времени.

Для быстрого тестирования была сделана функциональность для бенчмарка. Для получения данных для него я специальным скриптом спарсил 4683 цветных кроссворда (из 10906) и 1406 черно-белых (из 8293) с nonograms.ru (это один из крупнейших архивов нонограмм в интернете) и сохранил их в формате, понятном программе. Можно считать, что эти кроссворды являются случайной выборкой, поэтому бенчмарк показал бы адекватные средние значения. Также номера пары дюжин самых “сложных” кроссвордов (также самых больших по размеру и количеству цветов) записал в скрипт для загрузки ручками.

Оптимизация

Здесь показаны возможные приемы для оптимизации, которые были сделаны (1)во время написания всего алгоритма, (2)для ужимания времени работы с полминуты до долей секунды, (3)те оптимизации, которые могут быть полезны далее.

Во время написания алгоритма

Что уменьшает время работы

Этих правок оказалось достаточно, чтобы получить такие данные на бенчмарке:

Можно заметить, что в среднем черно-белые кроссворды “сложнее” цветных. Это подтверждает наблюдения любителей игры, которые также считают, что “цветные” решаются в среднем легче.

Таким образом, без радикальных правок (таких как переписывание всего кода на на С или ассемблерных вставок с fastcall и опусканием указателя фрейма) можно достичь высокой производительностью, заметим, на весьма скромном компьютере. К оптимизациям может быть применим принцип Парето — окажется, что мелкая оптимизация влияет сильно, потому что этот кусок кода критичен и вызывается очень часто.

Дальнейшая оптимизация

Следующие методы могут сильно улучшить производительность программы. Некоторые из них работают не во всех случаях, а при некоторых условиях.

Эти функции независимы друг от друга и у них нет общей памяти, кроме переменной solver (тип OneLineSolver), так что можно создать два объекта “решателя” (здесь очевидно только один — solver) и запустить два потока в этой же функции. Эффект такой — в цветных кроссвордах “самый тяжелый” решается в два раза быстрее, в черно-белых такой же на треть быстрее, а среднее время увеличилось, за счет сравнительно больших затрат на создание потоков.

Но вообще я бы не советовал делать прямо так в текущей программе и спокойно использовать — во-первых, создание потоков затратная операция, не стоит постоянно создавать потоки для микросекундных задач, во-вторых, при некоторой комбинации аргументов программы, потоки могут обращаться одновременно к какой-то внешней памяти, например при создании картинок решения — это надо бы учесть и обезопасить.

Если бы задача была серьезной и у меня было бы много данных и многоядерные машины, я бы пошел еще дальше — можно завести несколько постоянных потоков, у каждого будет свой объект OneLineSolver, и еще одна thread-safe структура, которая рулит распределением работы и по запросу к ней выдает референс на очередную строку/столбец для решения. Потоки после решения очередной задачи обращаются к структуре заново, чтобы решать что-то еще. Какую-то задачу-нонограмму в принципе можно начать решать, не закончив предыдущей, например когда эта структура занимается взаимным AND всех клеток, и тогда какие-то потоки свободны и ничего не делают. Еще распараллеливание можно провести на графическом процессоре через CUDA — вариантов много.

То есть работает за линию, за (Позже будет объяснение смысла именно такого кода).

К сожалению, особо сильные колдунства как алгоритм Фарака-Колтона и Бендера (предподсчет , запрос ) использовать нельзя, так как вкурив статьи, можно понять, они созданы только для таких операций , что , то есть результат коммутативной операции — один из аргументов (жаль, а так хотелось. )

Еще можно использовать расширение алгоритма для черного-белого кроссворда — частичные суммы для всех цветов.

Итак, возникает вопрос — почему мы не используем все это богатство комплюктерн саенс, а делаем за линию? На это есть несколько ответов:

То есть объяснение простое — оба этих пункта выполняются и вставка этих чудес программерской мысли вместо тупого алгоритма либо очень слабо оптимизирует программу, либо только увеличивает время работы из-за специфики вычислений — очень маленького и не такого большого количества запросов, чтобы они грузили процессор. Факт про запросы доказывает то, что по мнению профайлера те функции занимают

11% времени соответственно, то есть довольно мало для такого потенциально слабого места программы. Даже если у нас из-за этого возникает большая оценка сложности алгоритма, стоит понимать, что в таких типах задач это оценка сверху, а реальное время работы на рандомном кроссворде всегда премного ниже.

Но не стоит забывать про структуры данных — они могут пригодиться в других случаях, так что я включил их в список оптимизаций. Переходим к следующему по списку.

В общем, вот такие прикольные оптимизации. “Пихание” бедного алгоритма в зависимости от условий это весело и познавательно. Можно узнать про разные крутые вещи, как встроенное декартово дерево по неявному ключу в C++ (это rope, но велосипедная писанина практически всегда работает быстрее), особые встроенные сорта деревьев и спрятанный hashtable, работающий в 3-6 раза быстрее по вставке/удалению и в 4-10 раз по записи/чтению, чем unordered_map. Не говоря уже про различные нестандартные мазафаки со стороны, например из boost.

ROFL Omitting Format Language

Вдохновившись гениями давно минувших дней и их мыслительными продуктами, в частности совершенно новыми алгоритмами архивации и операционками с нескучными обоями, я также придумал принципиально новый формат картинок, основанный на японских кроссвордах и эффекте Даннинга-Крюгера.

ROFL — рекурсивный акроним, прямо как “GNU’s Not Unix”. Собственно, смысл формата в том, что картинка кодируется в виде японского кроссворда, а редактор, чтобы прочитать ее, должен решить этот кроссворд. Отсюда и слово Omitting в названии — формат как бы скрывает истинное положение дел в картинке (что, кстати, может быть полезным в криптографии: можно передавать японские кроссворды с зашифрованными в нем паролями — все хакеры повесятся).

Лучше, если формат был бы похож на Matroska — в начале файла 4 байта [52][4F][46][4C], затем в трех байтах размер картинки и количество цветов, потом описание цветов, потом цвета, каждый по 3 байта, и потом описание всех групп — длина, количество клеток и цвет.

Формат свободный, лицензия MIT, финансовые отчисления добровольные — мне на кофе, как автору.

Исходники

Исходники программы лежат на GitHub. У программы есть множество возможных аргументов, генерация кроссворда из картинки, генерация картинок из кроссворда (кстати, почти все картинки в статье сгенерированы через этот код). Дополнительными библиотеками были Magick++ и args.

Источник