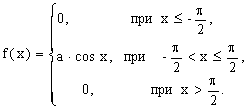Как найти параметр а в плотности распределения

Функция плотности распределения

Содержание:

Пусть имеется непрерывная случайная величина X с функцией распределения F (х), которую мы предположим непрерывной и дифференцируемой. Вычислим вероятность попадания этой случайной величины на участок от

т. е. приращение функции распределения на этом участке. Рассмотрим отношение этой вероятности к длине участка,- т. е. среднюю вероятность, приходящуюся на единицу длины на этом участке, и будем приближать к нулю.

В пределе получим производную от функции распределения:

Эта функция называется плотностъю распределения (иначе «плотностью вероятности») непрерывной случайной величины X. Иногда функцию f (х) называют также «дифференциальной функцией распределения» или «диффе-ренциальным законом распределения величины X.

По этой ссылке вы найдёте полный курс лекций по высшей математике:

Термины «плотность распределения», «плотность вероятности»

Термины «плотность распределения», «плотность вероятности» становятся особенно наглядными Рис. 5.4.1. при пользовании механической интерпретацией распределения; в этой интерпретации функция f (х) буквально характеризует плотность распределения масс по оси абсцисс (так называемую «линейную плотность»).

Кривая, изображающая плотность распределения случайной величины, называется кривой распределения (рис. 5.4.1).

Плотность распределения, так же как и функция распределения, есть одна из форм закона распределения. В противоположность функции распределения эта форма не является универсальной: она существует только для непрерывных случайных величин.

Рассмотрим непрерывную случайную величину X с плотностью распределения и элементарный участок dx, примыкающий к точке х (рис. 5.4.2). Вероят ность попадания случайной величины X

на этот элементарный участок (с точностью до бесконечно малых высшего порядка) равна f(x)dx. Величина f(x)dx называется элементом вероятности. Геометрически это есть площадь элементарного прямоугольника, опирающегося на отрезок dx (рис. 5.4.2).

Возможно вам будут полезны данные страницы:

Выразим вероятность попадания величины X на отрезок от а до 0 (рис. 5.4.3) через плотность распределения. Очевидно, она равна сумме элементов вероятности на всем этом участке, т. е. интегралу:

Геометрически вероятность попадания величины X на участок равна площади кривой распределения, опирающсйся на этот участок (рис. 5.4.3).

Формула (5.4.2) выражает плотность распределения через функцию распределения. Зададимся обратной задачей: выразить функцию распределения через плотность. По определению

откуда по формуле (5.4.3) имеем:

Геометрически F (х) есть не что иное, как площадь кривой распределения, лежащая левее точки х (рис. 5.4.4).

Укажем основные свойства плотности распределения:

1. Плотность распределения есть неотрицательная функция: Это свойство непосредственно вытекает из того, что функция распределения F (х) есть неубывающая функция.

2. Интеграл в бесконечных пределах от плотности распределения равен единице:

Это следует из формулы (5.4.4) и из того, что геометрически основные свойства плотности распределения означают, что:

Выясним размерности основных характеристик случайной величины — функции распределения и плотности распределения. Функция распределения F (х), как всякая вероятность, есть величина безразмерная. Размерность плотности распределения /(х), как видно из Формулы (5.4.1), обратна размерности случайной величины.

Примеры с решением

Пример 1. Функция распределения непрерывной случайной величины X задана выоажением

а) Найти коэффициент а.

б) Найти плотность распределения f (х).

в) Найти вероятность попадания величины X на участок от 0,25 до 0,5.

Решение:

а) Так как функция распределения величины X непрерывна, то при

б) Плотность распределения величины X выражается формулой

в) По формуле (5.3.1) имеем:

Пример 2. Случайная величина X подчинена закону распределения с плотностью:

а) Найти коэффициент а,

б) Построить график плотности распределения /(х).

в) Найти функцию распределения F (х) и построить ее график,

г) Найти вероятность попадания величины X на участок от

Решение:

а) Для определения коэффициента а воспользуемся свойством плотности распределения:

б) График плотности f (х) представлен на рис. 5.4.5.

в) По формуле (5.4.4) получаем выражение функции распределения:

График функции F (х) изображен на рис. 5.4.6.

г) По формуле (5.3.1.) имеем

Тот же результат, но несколько более сложным путем можно получить по формуле (.5.4.3).

Пример 3. Плотность распределения случайной величины X задана формулой:

а) Построить график плотности

б) Найти вероятность того, что величина X попадет на участок (—1,+1).

Решение:

а) График плотности дан на рис. 5.4.7.

б) По формуле (5.4.3) имеем:

Присылайте задания в любое время дня и ночи в whatsapp.

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Источник

Плотность распределения

Плотность распределения

Плотность распределения

Плотность распределения вероятностей непрерывной случайной величины

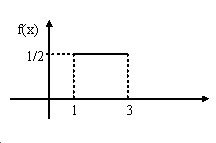
Решение. Построим график функции плотности распределения вероятностей.

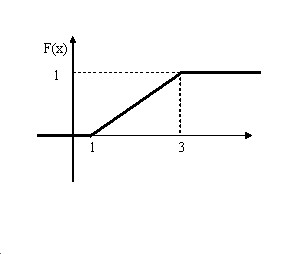
Построим график функции распределения

Свойства плотности распределения

Геометрически это означает, что площадь под кривой распределения равна 1.

Далее:

Критерий полноты

Криволинейный интеграл первого рода

СДНФ. Теорема о представлении в виде СДНФ. Построение СДНФ по таблице

Замена переменных в тройном интеграле

Вычисление тройного интеграла. Теорема о переходе от тройного интеграла к повторному

Свойства тройного интеграла

Примеры применения цилиндрических и сферических координат

Замена переменных в двойном интеграле. Двойной интеграл в полярных координатах

Вычисление криволинейного интеграла второго рода в случае выполнения условия независимости от формы

Критерий полноты <формулировка>. Лемма о несамодвойственной функции

Решение задач с помощью алгебры высказываний

Соленоидальное векторное поле

Введение

Упрощение логических функций

Источник

Математика — онлайн помощь

Свойство 1. Плотность распределения — неотрицательная функция: .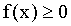

Доказательство. Функция распределения — неубывающая функция, следовательно, ее производная 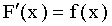— функция неотрицательная.

С геометрической точки зрения это означает, что точки, принадлежащие графику плотности распределения, расположены либо над осью Ох, либо на этой оси.

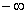
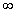
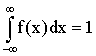
Свойство 2. Несобственный интеграл от плотности распределения в пределах от до равен единице:

.

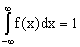
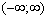
Доказательство. Несобственный интеграл выражает вероятность события, состоящего в том, что случайная величина примет значение, принадлежащее интервалу . Очевидно, такое событие достоверно, следовательно, вероятность его равна единице.

Геометрически это означает, что вся площадь криволинейной трапеции, ограниченной осью Ох и кривой распределения, равна единице.

В частности, если все возможные значения случайной величины принадлежат интервалу (a;b), то

.

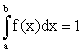
ПРИМЕР 13.1.44 Плотность распределения случайной величины Х задана:

Найти постоянный параметр а.

.

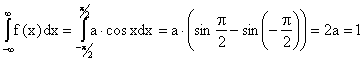
Таким образом, искомый параметр .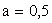

Уважаемые студенты
На нашем сайте можно получить помощь по всем разделам математики и другим предметам:
✔ Решение задач
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Источник

Непрерывная случайная величина, функция распределения и плотность вероятности

Определение непрерывной случайной величины и её связь с вероятностью

Случайной величиной называется переменная, которая может принимать те или иные значения в зависимости от различных обстоятельств, и случайная величина называется непрерывной, если она может принимать любое значение из какого-либо ограниченного или неограниченного интервала. Для непрерывной случайной величины невозможно указать все возможные значения, поэтому обозначают интервалы этих значений, которые связаны с определёнными вероятностями.

Примерами непрерывных случайных величин могут служить: диаметр детали, обтачиваемой до заданного размера, рост человека, дальность полёта снаряда и др.

Так как для непрерывных случайных величин функция F(x), в отличие от дискретных случайных величин, нигде не имеет скачков, то вероятность любого отдельного значения непрерывной случайной величины равна нулю.

Функция распределения непрерывной случайной величины и плотность вероятности

В качестве закона распределения, имеющего смысл только для непрерывных случайных величин, вводится понятие плотности распределения или плотности вероятности. Подойдём к нему путём сравнения смысла функции распределения для непрерывной случайной величины и для дискретной случайной величины.

Итак, функцией распределения случайной величины (как дискретной, так и непрерывной) или интегральной функцией называется функция , которая определяет вероятность, что значение случайной величины X меньше или равно граничному значению х.

Плотностью вероятности f(x) непрерывной случайной величины называется производная её функции распределения:

.

Зная функцию плотности, можно найти вероятность того, что значение непрерывной случайной величины принадлежит закрытому интервалу [a; b]:

вероятность того, что непрерывная случайная величина X примет какое-либо значение из интервала [a; b], равна определённому интегралу от её плотности вероятности в пределах от a до b:

.

При этом общая формула функции F(x) распределения вероятностей непрерывной случайной величины, которой можно пользоваться, если известна функция плотности f(x) :

.

График плотности вероятности непрерывной случайной величины называется её кривой распределения (рис. ниже).

Площадь фигуры (на рисунке заштрихована), ограниченной кривой, прямыми, проведёнными из точек a и b перпендикулярно оси абсцисс, и осью Ох, графически отображает вероятность того, что значение непрерывной случайной величины Х находится в пределах от a до b.

Свойства функции плотности вероятности непрерывной случайной величины

1. Вероятность того, что случайная величина примет какое-либо значение из интервала (и площадь фигуры, которую ограничивают график функции f(x) и ось Ох) равна единице:

2. Функция плотности вероятности не может принимать отрицательные значения:

,

а за пределами существования распределения её значение равно нулю

Плотность распределения f(x), как и функция распределения F(x), является одной из форм закона распределения, но в отличие от функции распределения, она не универсальна: плотность распределения существует только для непрерывных случайных величин.

Упомянем о двух важнейших в практике видах распределения непрерывной случайной величины.

Если функция плотности распределения f(x) непрерывной случайной величины в некотором конечном интервале [a; b] принимает постоянное значение C, а за пределами интервала принимает значение, равное нулю, то такое распределение называется равномерным.

Если график функции плотности распределения симметричен относительно центра, средние значения сосредоточены вблизи центра, а при отдалении от центра собираются более отличающиеся от средних (график функции напоминает разрез колокола), то такое распределение называется нормальным.

Пример 1. Известна функция распределения вероятностей непрерывной случайной величины:

Найти функцию f(x) плотности вероятности непрерывной случайной величины. Построить графики обеих функций. Найти вероятность того, что непрерывная случайная величина примет какое-либо значение в интервале от 4 до 8: .

Решение. Функцию плотности вероятности получаем, находя производную функции распределения вероятностей:

Найдём вероятность того, что непрерывная случайная величина примет какое либо значение в интервале от 4 до 8:

.

Пример 2. Функция плотности вероятности непрерывной случайной величины дана в виде:

Решение. Коэффициент C найдём, пользуясь свойством 1 функции плотности вероятности:

Таким образом, функция плотности вероятности непрерывной случайной величины:

.

Таким образом, полная запись функции распределения вероятностей:

Найдём вероятность того, что непрерывная случайная величина примет какое либо значение в интервале от 0 до 5:

.

Пример 3. Плотность вероятности непрерывной случайной величины X задана равенством , при этом . Найти коэффициент А, вероятность того, что непрерывная случайная величина X примет какое-либо значение из интервала ]0, 5[, функцию распределения непрерывной случайной величины X.

Решение. По условию приходим к равенству

.

Следовательно, , откуда . Итак,

.

Теперь находим вероятность того, что непрерывная случайная величина X примет какое-либо значение из интервала ]0, 5[:

Теперь получим функцию распределения данной случайной величины:

Пример 4. Найти плотность вероятности непрерывной случайной величины X, которая принимает только неотрицательные значения, а её функция распределения .

Решение. По определению плотности вероятности получаем

при и при , поскольку F(x) для этих значений x постоянна (равна нулю).

Пример 5. Плотность распределения непрерывной случайной величины задана формулой:

(при x > 0 )

1) найти функцию распределения непрерывной случайной величины;

2) найти вероятность того, что непрерывная случайная величина примет значение, лежащее между 1 и 2.

2) вероятность попадания непрерывной случайной величины на участок между 1 и 2 вычислим как приращение функции распределения на этом участке:

Пример 6. Непрерывная случайная величина имеет плотность

при .

1) найти вероятность попадания непрерывной случайной величины на участок от 0 до π/4;

2) функцию распределения непрерывной случайной величины.

1) находим вероятность:

.

2) находим функцию распределения непрерывной случайной величины:

Пример 7. Плотность распределения непрерывной случайной величины задана формулой

.

Найти вероятность попадания непрерывной случайной величины на участок (-1; +1)

.

Источник