как найти скорость электрона в магнитном поле
Как найти скорость электрона в магнитном поле
В некоторых электронных приборах используется влияние магнитного поля на движущиеся в нем электроны.
В § 3-2, в было получено выражение (3-6) для силы, с которой однородное магнитное поле действует на электрон, движущийся перпендикулярно направлению поля. Величина этой силы пропорциональна произведению магнитной индукции В, заряда электрона 

Из выражения силы (3-6) следует, что при 

Если на электрон действует только магнитное поле, то он будет перемещаться по окружности радиуса 
Сила F является центростремительной и уравновешивается центробежной силой электрона 
Так как эти силы равны, то можно написать
откуда определяется радиус, окружности
Отношение массы электрона к его заряду постоянно, следовательно, радиус окружности пропорционален скорости движения электрона и обратно пропорционален магнитной индукции поля.
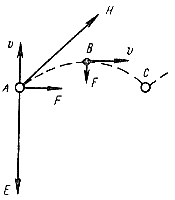
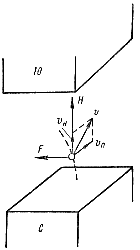
Рис. 13-4. Движение электрона в магнитном поле при начальной скорости v в плоскости, перпендикулярной вектору магнитной индукции поля.
Рис. 13-5. Движение электрона в магнитном поле при начальной скорости, направленной под острым углом к вектору магнитной индукции поля.
Если начальная скорость электрона не перпендикулярна направлению поля, то ее следует разложить на две составляющие: нормальную, т. е. перпендикулярную к направлению поля 

Первая составляющая скорости 

Как найти скорость электрона в магнитном поле
Рассмотрим снова движение электрона, находящегося в однородном магнитном поле. Мы ожидаем, что при малых скоростях электрона описанное ранее движение будет совпадать с тем, что мы получим сейчас. При больших скоростях существенную роль должны играть так называемые релятивистские поправки. Эта задача представляет интерес не только для сравнения нерелятивистских и релятивистских результатов, но имеет и чисто практическое значение. Дело в том, что в установках, ускоряющих электроны до релятивистских скоростей, часто используют постоянные однородные магнитные поля, удерживающие эти электроны на круговых орбитах.
Выражение для силы, действующей на движущийся электрон со стороны магнитного поля, было получено нами ранее:
Второй закон движения в форме Ньютона имеет вид
В рассматриваемом случае электрон движется по круговой орбите с ускорением 
(изменяется лишь направление скорости), данный случай особенно прост для исследования, так как величина 
В результате релятивистский закон движения можно записать в виде
Комбинируя второй закон Ньютона с выражением для силы, действующей на электрон со стороны магнитного поля, получаем
Отсюда находим напряженность магнитного поля, необходимую для удержания частицы на орбите радиусом
которую можно сравнить с определенной ранее напряженностью поля в нерелятивистском случае:
Эти напряженности отличаются множителем
Смысл полученного результата состоит в том, что в релятивистском случае требуется большее магнитное поле для удержания частицы с заданной скоростью на орбите заданного радиуса. Этот результат нетрудно понять. При заданных 




При желании можно считать, что разница между релятивистским и нерелятивистским выражениями целиком обусловлена изменением релятивистской массы электрона
возрастающей при увеличении его скорости (фиг. 47).
Измерение напряженности магнитного поля, удерживающего электрон со скоростью 



Фиг. 47. Зависимость массы от скорости.
Отсюда видно, что практические инженерные и экономические решения должны существенно зависеть от того, какие соотношения верны — релятивистские или нерелятивистские. Люди, имеющие отношение к подобным вещам, давно убедились в том, что справедливо релятивистское выражение, определяющее напряженность магнитного поля. Этот вывод был подтвержден так много раз и при таких разнообразных условиях, что сейчас уже потерял всякий смысл вопрос о том, проверена ли на опыте теория относительности. Она настолько хорошо проверена, что стала частью наших обычных представлений. Соотношения, вытекающие из теории относительности (подобно соотношениям геометрии Евклида), стали неотъемлемой частью нашего мышления и повсеместно используются инженерами, конструирующими ускорители частиц, в их практической деятельности. Вполне
возможно, что в будущем по неизвестным сейчас причинам эти представления (как и любые другие) придется уточнять. Но в настоящее время теория относительности внесла такую ясность в рассматриваемый круг явлений, что подобно геометрии Евклида в пространстве она заслужила титул «правдивой».
Максимальная скорость
Рассмотрим теперь поведение частицы, на которую действует постоянная однородная сила в заданном направлении. С точки зрения теории Ньютона такая частица будет испытывать постоянное ускорение, а ее скорость со временем будет неограниченно возрастать. Релятивистские уравнения можно записать в виде
где релятивистский импульс
В релятивистском случае импульс и энергия частицы, подверженной действию постоянной силы, непрерывно нарастают. Скорость же частицы не может превысить с.
Чтобы показать это, выразим из уравнения (31.3) скорость через импульс.
При заданной массе покоя и при больших значениях импульса это выражение можно приблизительно представить в виде
Таким образом, в пределе бесконечно больших значений импульса скорость 
Если действительно приложить к электрону постоянную силу (как, например, в эксперименте «Максимальная скорость» 
Таким образом, мы получили следующий практический результат: несмотря на то, что импульс и энергия электрона непрерывно увеличиваются, его скорость, т. е. пройденное электроном расстояние,
деленное на соответствующий отрезок времени, приближается к постоянной величине — скорости света.
На фиг. 48 изображена принципиальная схема установки для определения максимальной скорости электронов [3].
Электроны ускоряют в однородном поле в левой части установки. Моменты их пролета через точки А и В засекают с помощью осциллографа. Таким образом определяют скорость электронов.
Их кинетическую энергию (которая превращается в тепло при попадании электронов в мишень) определяют по измеренному повышению температуры мишени.
Если построить затем график зависимости кинетической энергии от 
(прямая линия на фиг. 49), а релятивистскому выражению
ДВИЖЕНИЕ ЭЛЕКТРОНОВ В ЭЛЕКТРИЧЕСКОМ И МАГНИТНОМ ПОЛЯХ
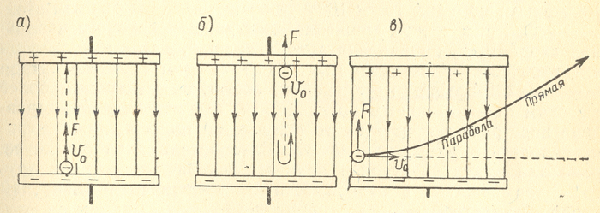
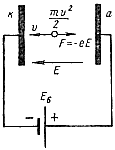
На рис.1 а, изображено электрическое поле в вакууме между двумя плоскими электродами. Они могут представлять собой катод и анод диода или любые два соседних электрода многоэлектродного прибора. Представим себе, что из электрода, имеющего более низкий потенциал, например из жатода, вылетает электрон с некоторой начальной скоростью Vo. Поле действует на электрон с силой F и ускоряет его движение к электроду, имеющему более высокий положительный потенциал, например к аноду. Иначе говоря, электрон притягивается к электроду с более высоким положительным потенциалом. Поэтому поле в данном случае называют ускоряющим. Двигаясь ускоренно, электрон приобретает наибольшую скорость в конце своего пути, т. е. при ударе об электрод, к которому он летит. В момент удара кинетическая энергия электрона также будет наибольшей. Таким образом, при движении электрона в ускоряющем поле происходит увеличение кинетической энергии электрона за счет того, что поле совершает работу по перемещению электрона. Электрон всегда отнимает энергию от ускоряющего поля.
Скорость, приобретаемая электроном при движении в ускоряющем поле, зависит исключительно от пройденной разности потенциалов U и определяется формулой
Удобно скорости электронов выражать условно в вольтах. Например, скорость электрона 10 в, означает такую скорость, которую электрон приобретает в результате движения в ускоряющем поле с разностью потенциалов 10 в. Из приведенной формулы легко найти, что при U — 100 в скорость V
6 000 км/сек. При таких больших скоростях время пролета электрона в пространстве между электродами получается весьма малым, порядка 10 в минус 8 — 10 в минус 10 сек.
Рассмотрим теперь движение электрона, у которого начальная скорость Vo направлена против силы F, действующей на электрон со стороны поля (рис.1 б). В этом случае электрон вылетает с некоторой начальной скоростью из электрода с более высоким положительным потенциалом. Та,к как сила F направлена навстречу скорости Vo, то получается торможение электрона и поле называют тормозящим. Следовательно, одно и то же поле для одних электронов является ускоряющим, а для других— тормозящим, в зависимости от направления начальной скорости электрона.
Движение электронов в электрическом и магнитном полях
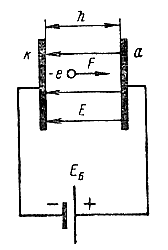
Если два плоских, параллельно расположенных электрода поместить в вакуум и подключить к источнику электродвижущей силы, то в пространстве между электродами образуется электрическое поле, силовые линии которого будут прямолинейны, параллельны друг другу и перпендикулярны к поверхностям обоих электродов.
Знак минус свидетельствует о том, что сила F, действующая на отрицательный заряд —е, и напряженность поля Е имеют противоположные направления. Для однородного электрического поля произведение напряженности Е на расстояние между электродами h равно приложенной разности потенциалов между электронами:
и U к и U а — потенциалы электродов к и а.



























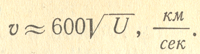
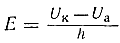
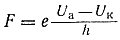 (2)
(2)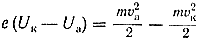
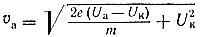 (4)
(4)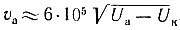 (5)
(5)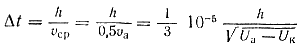 (6)
(6)
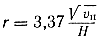 (8)
(8)