Как называется параметр определяемый по формуле t и измеряемый в рад с2
Формулы частоты вращения циклической. Определение частоты вращения вала
Одним из распространенных в природе и технике видов движения является вращение. Этот вид перемещения тел в пространстве характеризуется набором физических величин. Важная характеристика любого вращения — это частота. Формулу частоту вращения можно найти, зная определенные величины и параметры.
Что такое вращение?
Под ним в физике понимают такое перемещение материальной точки вокруг некоторой оси, при котором ее расстояние до этой оси остается постоянным. Оно называется радиусом вращения.

Примерами этого движения в природе является вращение планет вокруг Солнца и вокруг собственной оси. В технике вращение представлено движением валов, шестеренок, колеса автомобиля или велосипеда, перемещением лопастей ветровых мельниц.
Описывающие вращение физические величины
Для численного описания вращения в физике был введен ряд характеристик. Перечислим их и охарактеризуем.
В первую очередь это угол поворота, обозначается θ. Поскольку полная окружность характеризуется центральным углом в 2*pi радиан, то, зная величину θ, на которую повернулось вращающееся тело за определенный промежуток времени, можно определить число оборотов за это время. Кроме того, угол θ позволяет рассчитать линейный путь, пройденный телом вдоль кривой окружности. Соответствующие формулы для числа оборотов n и пройденного пути L имеют вид:
Где r — радиус окружности или радиус вращения.
Следующей характеристикой рассматриваемого типа движения является угловая скорость. Ее обычно обозначают буквой ω. Она измеряется в радианах в секунду, то есть показывает величину угла в радианах, на которые поворачивается вращающееся тело за одну секунду. Для угловой скорости в случае равномерного вращения справедлива формула:
Угловая частота, период и угловая скорость
Выше уже отмечалось, что важным свойством любого вращательного движения является время, за которое совершается один оборот. Это время называется периодом вращения. Его обозначают буквой T и измеряют в секундах. Формулу для периода T можно записать через угловую скорость ω. Соответствующее выражение имеет вид:
Величина, обратная периоду, называется частотой. Ее измеряют в герцах (Гц). Для кругового движения удобно использовать не саму частоту, а ее угловой аналог. Обозначим ее f. Формула частоты вращения угловой f имеет вид:
Чтобы рассчитать угловую частоту, необходимо знать период вращательного движения.
Сравнивая две последние формулы, приходим к следующему равенству:
Это равенство означает следующее:
Различие между этими величинами единственное: угловая частота является величиной скалярной, скорость же — это вектор.
Линейная скорость вращения, частота и частота угловая
В технике для некоторых вращающих конструкций, например, шестерен и валов, известны их рабочие частоты μ и линейные скорости v. Тем не менее каждую из этих характеристик можно использовать для определения угловой или циклической частоты.
Выше отмечалось, что частота μ измеряется в герцах. Она показывает количество оборотов вращающегося тела за одну секунду. Формула для нее принимает вид:
Если сравнить это выражение с соответствующим равенством для f, то формула, как найти частоту вращения f через μ описывающая, будет иметь вид:
Эта формула интуитивно понятна, поскольку μ показывает количество оборотов за единицу времени, а f отражает ту же самую величину, только представленную в радианах.
Линейная скорость v связана со скоростью угловой ω следующим равенством:
Поскольку модули величин f и ω равны, то из последнего выражения легко получить соответствующую формулу частоты вращения циклической. Запишем ее:
Где r — радиус вращения. Заметим, что скорость v линейно растет при увеличении радиуса r, при этом отношение этих величин является константой. Последнее умозаключение означает, что если измерять циклическую частоту вращения в любой точке сечения вращающегося массивного объекта, то она будет везде одинаковой.
Задача на определение циклической частоты вращения вала
Угловые частоты вращения содержат полезную информацию, поскольку позволяют рассчитать такие важные физические характеристики, как момент импульса или угловую скорость. Решим такую задачу: известно, что рабочая частота вращения вала составляет 1500 оборотов в минуту. Чему равна циклическая частота для этого вала?
Из единиц измерения, приведенный в условии, понятно, что дана обычная частота μ. Поэтому формула частоты вращения вала циклической имеет вид:
Прежде чем ею пользоваться, следует перевести указанную в условии цифру к стандартным единицам измерения, то есть к обратным секундам. Поскольку вал за минуту делает 1500 оборотов, то за секунду он сделает в 60 раз меньше оборотов, то есть 25. То есть частота его вращения равна 25 Гц. Подставляя это число в записанную выше формулу, получаем значение циклической частоты: f = 157 рад/с.
Как называется параметр определяемый по формуле t и измеряемый в рад с2
При движении по окружности с постоянной по величине линейной скоростью v тело испытывает направленное к центру окружности постоянное центростремительное ускорение
Вывод формулы для центростремительного ускорения
По определению
На рисунке треугольники, образованные векторами перемещений и скоростей, подобны. Учитывая, что |r1| = |r2| = R и |v1| = |v2| = v, из подобия треугольников находим:
откуда
Поместим начало координат в центр окружности и выберем плоскость, в которой лежит окружность, за плоскость (x, y). Положение точки на окружности в любой момент времени однозначно определяется полярным углом j, измеряемым в радианах (рад), причем
x = R cos(j + j0), y = R sin(j + j0),
где j0 определяет начальную фазу (начальное положение точки на окружности в нулевой момент времени).
В случае равномерного вращения угол j, измеряемый в радианах, линейно растет со временем:
Циклическая частота равна величине угла поворота (измеренном в рад) за единицу времени, так что иначе ее называют угловой скоростью.
Зависимость координат точки на окружности от времени в случае равномерного вращения с заданной частотой можно записать в виде:
Время, за которое совершается один оборот, называется периодом T.
Связь циклической частоты с периодом и частотой: 2p = wT, откуда
Связь линейной скорости и угловой скорости находится из равенства: 2pR = vT, откуда
Выражение для центростремительного ускорения можно записать разными способами, используя связи между скоростью, частотой и периодом:
Связь поступательного и вращательного движений
Основные кинематические характеристики движения по прямой с постоянным ускорением: перемещение s, скорость v и ускорение a. Соответствующие характеристики при движении по окружности радиусом R: угловое перемещение j, угловая скорость w и угловое ускорение a (в случае, если тело вращается с переменной скоростью). Из геометрических соображений вытекают следующие связи между этими характеристиками:
Все формулы кинематики равноускоренного движения по прямой могут быть превращены в формулы кинематики вращения по окружности, если сделать указанные замены. Например:
s = vt
j = wt,
v = v0 + atw = w0 + at.
Связь между линейной и угловой скоростями точки при вращении по окружности можно записать в векторной форме. Действительно, пусть окружность с центром в начале координат расположена в плоскости (x, y). В любой момент времени вектор R, проведенный из начала координат в точку на окружности, где находится тело, перпендикулярен вектору скорости тела v, направленному по касательной к окружности в этой точке. Определим вектор w, который по модулю равен угловой скорости w и направлен вдоль оси вращения в сторону, которая определяется правилом правого винта: если завинчивать винт так, чтобы направление его вращения совпадало с направлением вращения точки по окружности, то направление движения винта показывает направление вектора w. Тогда связь трех взаимно перпендикулярных векторов R, v и w можно записать с помощью векторного произведения векторов:
Характеристики колебаний
Чтобы описать колебательные процессы и отличить одни колебания от других, используют 6 характеристик. Они называются так (рис. 1):
Такие величины, как амплитуду и период, можно определить по графику колебаний.
Начальную фазу, так же, определяют по графику, с помощью интервала времени \(\large \Delta t\), на который относительно нуля сдвигается начало ближайшего периода.
Частоту и циклическую частоту вычисляют из найденного по графику периода, по формулам. Они находятся ниже в тексте этой статьи.
А фазу определяют с помощью формулы, в которую входит интересующий нас момент времени t колебаний. Читайте далее.
Что такое амплитуда
Амплитуда – это наибольшее отклонение величины от равновесия, то есть, максимальное значение колеблющейся величины.
Измеряют в тех же единицах, в которых измерена колеблющаяся величина. К примеру, когда рассматривают механические колебания, в которых изменяется координата, амплитуду измеряют в метрах.
В случае электрических колебаний, в которых изменяется заряд, ее измеряют в Кулонах. Если колеблется ток – то в Амперах, а если – напряжение, то в Вольтах.
Часто обозначают ее, приписывая к букве, обозначающей амплитуду индекс «0» снизу.
К примеру, пусть колеблется величина \( \large x \). Тогда символом \( \large x_ <0>\) обозначают амплитуду колебаний этой величины.
Иногда для обозначения амплитуды используют большую латинскую букву A, так как это первая буква английского слова «amplitude».
С помощью графика амплитуду можно определить так (рис. 2):
Что такое период
Когда колебания повторяются точно, изменяющаяся величина принимает одни и те же значения через одинаковые кусочки времени. Такой кусочек времени называют периодом.
Обозначают его обычно большой латинской буквой «T» и измеряют в секундах.
\( \large T \left( c \right) \) – период колебаний.
Одна секунда – достаточно большой интервал времени. Поэтому, хотя период и измеряют в секундах, но для большинства колебаний он будет измеряться долями секунды.
Чтобы по графику колебаний определить период (рис. 3), нужно найти два одинаковых значения колеблющейся величины. После, провести от этих значений к оси времени пунктиры. Расстояние между пунктирами – это период колебаний.
Период – это время одного полного колебания.
На графике период найти удобнее одним из таких способов (рис. 4):
Что такое частота
Обозначают ее с помощью греческой буквы «ню» \( \large \nu \).
Частота отвечает на вопрос: «Сколько полных колебаний выполняется за одну секунду?» Или же: «Сколько периодов умещается в интервал времени, равный одной секунде?».
Поэтому, размерность частоты — это единицы колебаний в секунду:
\( \large \nu \left( \frac<1>
Иногда в учебниках встречается такая запись \( \large \displaystyle \nu \left( c^ <-1>\right) \), потому, что по свойствам степени \( \large \displaystyle \frac<1>
Начиная с 1933 года частоту указывают в Герцах в честь Генриха Рудольфа Герца. Он совершил значимые открытия в физике, изучал колебания и доказал, что существуют электромагнитные волны.
Одно колебание в секунду соответствует частоте в 1 Герц.
Чтобы с помощью графика определить частоту, нужно на оси времени определить период. А затем посчитать частоту по такой формуле:
Существует еще один способ определить частоту с помощью графика колеблющейся величины. Нужно отмерить на графике интервал времени, равный одной секунде, и сосчитать количество периодов колебаний, уместившихся в этот интервал (рис. 5).
Что такое циклическая частота
Колебательное движение и движение по окружности имеют много общего – это повторяющиеся движения. Одному полному обороту соответствует угол \(\large 2\pi\) радиан. Поэтому, кроме интервала времени 1 секунда, физики используют интервал времени, равный \(\large 2\pi\) секунд.
Число полных колебаний для такого интервала времени, называется циклической частотой и обозначается греческой буквой «омега»:
\( \large \displaystyle \omega \left( \frac<\text<рад>>
Примечание: Величину \( \large \omega \) так же называют круговой частотой, а еще — угловой скоростью (ссылка).
Циклическая частота отвечает на вопрос: «Сколько полных колебаний выполняется за \(\large 2\pi\) секунд?» Или же: «Сколько периодов умещается в интервал времени, равный \(\large 2\pi\) секунд?».
Обычная \( \large \nu \) и циклическая \( \large \omega \) частота колебаний связаны формулой:
Слева в формуле количество колебаний измеряется в радианах на секунду, а справа – в Герцах.
Чтобы с помощью графика колебаний определить величину \( \large \omega \), нужно сначала найти период T.
Затем, воспользоваться формулой \( \large \displaystyle \nu = \frac<1>
И только после этого, с помощью формулы \( \large \omega = 2\pi \cdot \nu \) посчитать циклическую \( \large \omega \) частоту.
Для грубой устной оценки можно считать, что циклическая частота превышает обычную частоту примерно в 6 раз численно.
Определить величину \( \large \omega \) по графику колебаний можно еще одним способом. На оси времени отметить интервал, равный \(\large 2\pi\), а затем, сосчитать количество периодов колебаний в этом интервале (рис. 6).
Что такое начальная фаза и как определить ее по графику колебаний
Отклоним качели на некоторый угол от равновесия и будем удерживать их в таком положении. Когда мы отпустим их, качели начнут раскачиваться. А старт колебаний произойдет из угла, на который мы их отклонили.
Такой, начальный угол отклонения, называют начальной фазой колебаний. Обозначим этот угол (рис. 7) какой-нибудь греческой буквой, например, \(\large \varphi_ <0>\).
\(\large \varphi_ <0>\left(\text <рад>\right) \) — начальная фаза, измеряется в радианах (или градусах).
Начальная фаза колебаний – это угол, на который мы отклонили качели, перед тем, как их отпустить. Из этого угла начнется колебательный процесс.
Рассмотрим теперь, как величина \(\large \varphi_ <0>\) влияет на график колебаний (рис. 8). Для удобства будем считать, что мы рассматриваем колебания, которые происходят по закону синуса.
Кривая, обозначенная черным на рисунке, начинает период колебаний из точки t = 0. Эта кривая является «чистым», не сдвинутым синусом. Для нее величину начальной фазы \(\large \varphi_ <0>\) принимаем равной нулю.
Вторая кривая на рисунке обозначена красным цветом. Начало ее периода сдвинуто вправо относительно точки t = 0. Поэтому, для красной кривой, начавшей новый период колебаний спустя время \(\large \Delta t\), начальный угол \(\large \varphi_ <0>\) будет отличаться от нулевого значения.
Определим угол \(\large \varphi_ <0>\) с помощью графика колебаний.
Обратим внимание (рис. 8) на то, что время, лежащее на горизонтальной оси, измеряется в секундах, а величина \(\large \varphi_ <0>\) — в радианах. Значит, нужно связать формулой кусочек времени \(\large \Delta t\) и соответствующий ему начальный угол \(\large \varphi_ <0>\).
Как вычислить начальный угол по интервалу смещения
Алгоритм нахождения начального угла состоит из нескольких несложных шагов.
\[\large T = 5 – 1 = 4 \left( \text <сек>\right)\]
Из графика следует, что период T = 4 сек.
Полученное значение дроби означает, что красная кривая сдвинута относительно точки t = 0 и черной кривой на четверть периода.
Для этого используем формулу:
\(\large \displaystyle \frac<1> <4>\cdot 2\pi = \frac<\pi > <2>=\varphi_ <0>\)
Значит, интервалу \(\large \Delta t\) соответствует угол \(\large \displaystyle \frac<\pi > <2>\) – это начальная фаза для красной кривой на рисунке.
Чтобы обозначить запаздывание, будем использовать знак «минус» для начального угла:
Примечание: Если на кривой колебаний начало ближайшего периода лежит левее точки t = 0, то в таком случае, угол \(\large \displaystyle \frac<\pi > <2>\) имеет знак «плюс».
Для не сдвинутого влево, либо вправо, синуса или косинуса, начальная фаза нулевая \(\large \varphi_ <0>= 0 \).
Для синуса или косинуса, сдвинутого влево по графику и опережающего обычную функцию, начальная фаза берется со знаком «+».
А если функция сдвинута вправо и запаздывает относительно обычной функции, величину \(\large \varphi_ <0>\) записываем со знаком «-».
Примечания:
Благодаря таким допущениям график колебаний при решении большинства задач можно изображать, начиная из окрестности нуля и преимущественно в правой полуплоскости.
Что такое фаза колебаний
Рассмотрим еще раз обыкновенные детские качели (рис. 9) и угол их отклонения от положения равновесия. С течением времени этот угол изменяется, то есть, он зависит от времени.
В процессе колебаний изменяется угол отклонения от равновесия. Этот изменяющийся угол называют фазой колебаний и обозначают \(\varphi\).
Различия между фазой и начальной фазой
Существуют два угла отклонения от равновесия – начальный, он задается перед началом колебаний и, угол, изменяющийся во время колебаний.
Первый угол называют начальной \( \varphi_<0>\) фазой (рис. 10а), она считается неизменной величиной. А второй угол – просто \( \varphi\) фазой (рис. 10б) – это величина переменная.
Как на графике колебаний отметить фазу
На графике колебаний фаза \(\large \varphi\) выглядит, как точка на кривой. С течением времени эта точка сдвигается (бежит) по графику слева направо (рис. 11). То есть, в разные моменты времени она будет находиться на различных участках кривой.
На рисунке отмечены две крупные красные точки, они соответствуют фазам колебаний в моменты времени t1 и t2.
А начальная фаза на графике колебаний выглядит, как место, в котором находится точка, лежащая на кривой колебаний, в момент времени t=0. На рисунке дополнительно присутствует одна мелкая красная точка, она соответствует начальной фазе колебаний.
Как определить фазу с помощью формулы
Пусть нам известны величины \(\large \omega\) — циклическая частота и \(\large \varphi_<0>\) — начальная фаза. Во время колебаний эти величины не изменяются, то есть, являются константами.
Время колебаний t будет величиной переменной.
Фазу \(\large \varphi\), соответствующую любому интересующему нас моменту t времени, можно определить из такого уравнения:
Левая и правая части этого уравнения имеют размерность угла (т. е. измеряются в радианах, или градусах). А подставляя вместо символа t в это уравнение интересующие нас значения времени, можно получать соответствующие им значения фазы.
Что такое разность фаз
Обычно понятие разности фаз применяют, когда сравнивают два колебательных процесса между собой.
Рассмотрим два колебательных процесса (рис. 12). Каждый имеет свою начальную фазу.
\( \large \varphi_<01>\) – для первого процесса и,
\( \large \varphi_<02>\) – для второго процесса.
Определим разность фаз между первым и вторым колебательными процессами:
Величина \(\large \Delta \varphi \) показывает, на сколько отличаются фазы двух колебаний, она называется разностью фаз.
Как связаны характеристики колебаний — формулы
Движение по окружности и колебательное движение имеют определенную схожесть, так как эти виды движения могут быть периодическими.
Поэтому, основные формулы, применимые для движения по окружности, подойдут так же, для описания колебательного движения.
\( \large T \left( c \right) \) – время одного полного колебания (период колебаний);
\( \large N \left( \text <шт>\right) \) – количество полных колебаний;
\( \large t \left( c \right) \) – общее время для нескольких колебаний;
\(\large \nu \left( \text <Гц>\right) \) – частота колебаний.
\(\large \displaystyle \omega \left( \frac<\text<рад>>
\(\large \varphi_ <0>\left( \text <рад>\right) \) — начальная фаза;
\(\large \varphi \left( \text <рад>\right) \) – фаза (угол) в выбранный момент времени t;
\(\large \Delta t \left( c \right) \) — интервал времени, на который относительно точки t=0 сдвинуто начало ближайшего периода.
Виброускорение, виброскорость и виброперемещение
В чём измеряют вибрацию?
Для количественного описания вибрации вращающегося оборудования и в диагностических целях используют виброускорение, виброскорость и виброперемещение.
Виброускорение
Виброускорение измеряется в:
AdB = 20 * lg10(A) + 120
AdB – виброускорение в децибелах
lg10 – десятичный логарифм (логарифм по основанию 10)
A – виброускорение в м/с 2
120 дБ – уровень 1 м/с 2
A = 10^((AdB-120)/20)
Например, 140 дБ = уровень 10 м/с 2 = 1 G
Виброскорость
Виброскорость – это скорость перемещения контролируемой точки оборудования во время её прецессии вдоль оси измерения.
В практике измеряется обычно не максимальное значение виброскорости, а ее среднеквадратичное значение, СКЗ (RMS). Физическая суть параметра СКЗ виброскорости состоит в равенстве энергетического воздействия на опоры машины реального вибросигнала и фиктивного постоянного, численно равного по величине СКЗ. Использование значения СКЗ обусловлено ещё и тем, что раньше измерения вибрации велись стрелочными приборами, а они все по принципу действия являются интегрирующими, и показывают именно среднеквадратичное значение переменного сигнала.
Из двух широко применяемых на практике представлений вибросигналов (виброскорость и виброперемещение) предпочтительнее использование виброскорости, так как это параметр, сразу учитывающий и перемещение контролируемой точки и энергетическое воздействие на опоры от сил, вызвавших вибрацию. Информативность виброперемещения может сравниться с информативностью виброскорости только при условии, когда дополнительно, кроме размаха колебаний, будут учтены частоты, как всего колебания, так и его отдельных составляющих. На практике сделать это весьма проблематично.
Для измерения СКЗ виброскорости используются самые простые приборы – виброметры. В более сложных приборах (виброанализаторах) также всегда присутствует режим виброметра.
Виброскорость измеряется в:
VdB = 20 * lg10(V) + 86
VdB – виброскорость в децибелах
lg10 – десятичный логарифм (логарифм по основанию 10)
V – виброскорость в мм/с
86 дБ – уровень 1 мм/с
Ниже приведены значечения виброскорости в дБ для стандартного ряда норм вибрации. Видно, что разница между соседними значениями – 4 дБ. Это соответствует разнице в 1,58 раза.
| мм/с | дБ |
| 45 | 119 |
| 28 | 115 |
| 18 | 111 |
| 11,2 | 107 |
| 7,1 | 103 |
| 4,5 | 99 |
| 2,8 | 95 |
| 1,8 | 91 |
| 1,12 | 87 |
| 0,71 | 83 |
Виброперемещение
Виброперемещение (вибросмещение, смещение) показывает максимальные границы перемещения контролируемой точки в процессе вибрации. Обычно отображается размахом (двойной амплитудой, Пик-Пик, Peak to peak). Виброперемещение – это растояние между крайними точками перемещения элемента вращающегося оборудования вдоль оси измерения.
Виброперемещение измеряется в линейных единицах:
Видео от Сергея Бойкина
Автор: Андрей Щекалев
Напишите мне свой вопрос, я отвечу Вам и дополню статью полезной информацией.
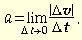
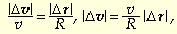
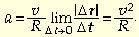
 j = wt,
j = wt, 











