Как называется сигнал параметры которого принимают конечное число значений
MT1402: Теоретические основы информатики. Имитационное моделирование
В предыдущем пункте было сказано, что передача информации производится с помощью сигналов, а самим сигналом является изменение некоторой характеристики носителя с течением времени. При этом в зависимости от особенностей изменения этой характеристики (т.е. параметра сигнала) с течением времени выделяют два типа сигналов: непрерывные и дискретные.
Сигнал называется непрерывным (или аналоговым), если его параметр может принимать любое значение в пределах некоторого интервала.
Сигнал называется дискретным, если его параметр может принимать конечное число значений в пределах некоторого интервала.
Пример дискретных сигналов представлен на рис. 1.1,б. Как следует из определения, дискретные сигналы могут быть описаны дискретным и конечным множеством значений параметров
Принципиальным и важнейшим различием непрерывных и дискретных сигналов является то, что дискретные сигналы можно обозначить, т.е. приписать каждому из конечного чисел возможные значения сигнала знак, который будет отличать данный сигнал от другого
Набор знаков, в котором установлен порядок их следования, называется алфавитом.
Представляется важным еще раз подчеркнуть, что понятия знака и алфавита можно отнести только к дискретным сообщениям.
INFOблог
Поиск по этому блогу
воскресенье, 8 сентября 2013 г.
Непрерывные и дискретные сигналы
Тогда материальный объект (или среда), с помощью которого представляется та или иная информация будет являться носителем информации , а изменение какой-либо характеристики носителя мы будем называть сигналом .
Например, представим равномерно горящую лампочку, она не передает никакой информации. Но, если мы будем включать и выключать лампочку (т.е. изменять ее яркость), тогда с помощью чередований вспышек и пауз мы сможем передать какое-нибудь сообщение (например, посредством азбуки Морзе). Аналогично, равномерный гул не дает возможности передать какую-либо информацию, однако, если мы будем изменять высоту и громкость звука, то сможем сформировать некоторое сообщение (что мы и делаем с помощью устной речи).
При этом сигналы могут быть двух видов: непрерывный (или аналоговый ) и дискретный .
В учебнике даны следующие определения.
Непрерывный сигнал принимает множество значений из некоторого диапазона. Между значениями, которые он принимает, нет разрывов.
Дискретный сигнал принимает конечное число значений. Все значения дискретного сигнала можно пронумеровать целыми числами.
Немного уточним эти определения.
Сигнал называется непрерывным (или аналоговым), если его параметр может принимать любое значение в пределах некоторого интервала.
3. Формы представления информации
Сигнал называется непрерывным (или аналоговым), если его параметр может принимать любое значение в пределах некоторого интервала
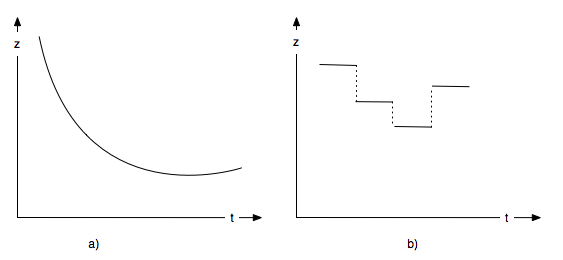
Если обозначить Z- значение параметра сигнала, at- время, то зависимость Z(t) будет непрерывной функцией (рис.1.2,а).
Рис. 1.2. Непрерывные (а) и дискретные (б) сигналы
Сигнал называется дискретным, если его параметр может принимать конечное число значений в пределах некоторого интервала.
Пример дискретных сигналов представлен на рис. 1.2,б. Как следует из определения, дискретные сигналы могут быть описаны дискретным и конечным множеством значений параметров
Принципиальным и важнейшим различием непрерывных и дискретных сигналов является то, что дискретные сигналы можно обозначить, т.е. приписать каждому из конечного чисел возможные значения сигнала знак, который будет отличать данный сигнал от другого.
Вся совокупность знаков, используемых для представления дискретной информации, называется набором знаков.
Таким образом, набор есть дискретное множество знаков.
Набор знаков, в котором установлен порядок их следования, называется алфавитом.
Понятия знака и алфавита можно отнести только к дискретным сообщениям.
Так как имеются два типа сообщений, между ними, возможны четыре варианта преобразований (см. рис. 1.3):
Рис. 1.3. Варианты преобразований
Осуществимы и применяются на практике все четыре вида преобразований. Примерами устройств, в которых осуществляется преобразование типа N1 → N2 являются микрофон (звук преобразуется в электрические сигналы); магнитофон и видеомагнитофон (чередование областей намагничения ленты превращается в электрические сигналы, которые затем преобразуются в звук и изображение); телекамера (изображение и звук превращаются в электрические сигналы); радио- и телевизионный приемник (радиоволны преобразуются в электрические сигналы, а затем в звук и изображение); аналоговая вычислительная машина (одни электрические сигналы преобразуются в другие). Особенностью данного варианта преобразования является то, что оно всегда сопровождается частичной потерей информации. Потери связаны с помехами (шумами), которые порождает само информационное техническое устройство и которые воздействуют извне. Эти помехи примешиваются к основному сигналу и искажают его. Поскольку параметр сигнала может иметь любые значения (из некоторого интервала), то невозможно отделить ситуации: был ли сигнал искажен или он изначально имел такую величину. (В ряде устройств искажение происходит в силу особенностей преобразования в них сообщения, например в черно-белом телевидении теряется цвет изображения; телефон пропускает звук в более узком частотном интервале, чем интервал человеческого голоса; кино- и видеоизображение оказываются плоскими, они утратили объемность.)
Развертка по времени состоит в том, что наблюдение за значением величины Z производится не непрерывно, а лишь в определенные моменты времени с интервалом Δt:
Совместное выполнение обеих операций эквивалентно нанесению масштабной сетки на график Z(t), как показано на рис.1.4. Далее, в качестве пар значений
Рис. 1.4. Дискретизация аналогового сигнала за счет операций развертки по времени и квантования по величине
Ответом на эти сомнения служит так называемая теорема отсчетов, доказанная в 1933г. В. А. Котельниковым (по этой причине ее иногда называют его именем), значение которой для решения проблем передачи информации было осознано лишь в 1948г. после работ К. Шеннона. Теорема, которую примем без доказательства, но результаты будем в дальнейшем использовать, гласит:
Непрерывный сигнал можно полностью отобразить и точно воссоздать по последовательности измерений или отсчетов величины этого сигнала через одинаковые интервалы времени, меньшие или равные половине периода максимальной частоты, имеющейся в сигнале.
Комментарии к теореме:
Теорема касается только тех линий связи, в которых для передачи используются колебательные или волновые процессы.
Смысл теоремы в том, что дискретизация не приведет к потере информации и по дискретным сигналам можно будет полностью восстановить исходный аналоговый сигнал, если развертка по времени выполнена в соответствии со следующим соотношением:
Можно перефразировать теорему отсчетов:
Развертка по времени может быть осуществлена без потери информации, связанной с особенностями непрерывного (аналогового) сигнала, если шаг развертки не будет превышать Δt, определяемый в соответствии с (1.2).
Например, для точной передачи речевого сигнала с частотой до Vm = 4000 Гц при дискретной записи должно производиться не менее 8000 отсчетов в секунду; в телевизионном сигнале Vm ≈ 4 МГц, следовательно, для его точной передачи потребуется около 8000000 отсчетов в секунду.
Выбор шага развертки по времени и квантования по величине сигнала лежат в основе оцифровки звука и изображения. Примерами устройств, в которых происходят такие преобразования, являются сканер, модем, устройства для цифровой записи звука и изображения, лазерный проигрыватель, графопостроитель. Термины «цифровая запись», «цифровой сигнал» следует понимать как дискретное представление с применением двоичного цифрового алфавита.
Таким образом, преобразование сигналов типа N → D, как и обратное D → N, может осуществляться без потери, содержащейся в них информации.
Таким образом, за исключением N1 → N2 в остальных случаях оказывается возможным преобразование сообщений без потерь содержащейся в них информации. При этом на первый взгляд непрерывные и дискретные сообщения оказываются равноправными. Однако на самом деле это не так. Сохранение информации в преобразованиях N → D и D → N обеспечивается именно благодаря участию в них дискретного представления. Другими словами, преобразование сообщений без потерь информации возможно только в том случае, если хотя бы одно из них является дискретным. В этом проявляется несимметричность видов сообщений и преимущество дискретной формы. К другим ее достоинствам следует отнести:
• простоту и, как следствие, надежность и относительную дешевизну устройств по обработке информации;
• точность обработки информации, которая определяется количеством обрабатывающих элементов и не зависит от точности их изготовления;
3. Формы представления информации
Сигнал называется непрерывным (или аналоговым), если его параметр может принимать любое значение в пределах некоторого интервала
Если обозначить Z- значение параметра сигнала, at- время, то зависимость Z(t) будет непрерывной функцией (рис.1.2,а).
Рис. 1.2. Непрерывные (а) и дискретные (б) сигналы
Сигнал называется дискретным, если его параметр может принимать конечное число значений в пределах некоторого интервала.
Пример дискретных сигналов представлен на рис. 1.2,б. Как следует из определения, дискретные сигналы могут быть описаны дискретным и конечным множеством значений параметров
Принципиальным и важнейшим различием непрерывных и дискретных сигналов является то, что дискретные сигналы можно обозначить, т.е. приписать каждому из конечного чисел возможные значения сигнала знак, который будет отличать данный сигнал от другого.
Вся совокупность знаков, используемых для представления дискретной информации, называется набором знаков.
Таким образом, набор есть дискретное множество знаков.
Набор знаков, в котором установлен порядок их следования, называется алфавитом.
Понятия знака и алфавита можно отнести только к дискретным сообщениям.
Так как имеются два типа сообщений, между ними, возможны четыре варианта преобразований (см. рис. 1.3):
Рис. 1.3. Варианты преобразований
Осуществимы и применяются на практике все четыре вида преобразований. Примерами устройств, в которых осуществляется преобразование типа N1 → N2 являются микрофон (звук преобразуется в электрические сигналы); магнитофон и видеомагнитофон (чередование областей намагничения ленты превращается в электрические сигналы, которые затем преобразуются в звук и изображение); телекамера (изображение и звук превращаются в электрические сигналы); радио- и телевизионный приемник (радиоволны преобразуются в электрические сигналы, а затем в звук и изображение); аналоговая вычислительная машина (одни электрические сигналы преобразуются в другие). Особенностью данного варианта преобразования является то, что оно всегда сопровождается частичной потерей информации. Потери связаны с помехами (шумами), которые порождает само информационное техническое устройство и которые воздействуют извне. Эти помехи примешиваются к основному сигналу и искажают его. Поскольку параметр сигнала может иметь любые значения (из некоторого интервала), то невозможно отделить ситуации: был ли сигнал искажен или он изначально имел такую величину. (В ряде устройств искажение происходит в силу особенностей преобразования в них сообщения, например в черно-белом телевидении теряется цвет изображения; телефон пропускает звук в более узком частотном интервале, чем интервал человеческого голоса; кино- и видеоизображение оказываются плоскими, они утратили объемность.)
Развертка по времени состоит в том, что наблюдение за значением величины Z производится не непрерывно, а лишь в определенные моменты времени с интервалом Δt:
Совместное выполнение обеих операций эквивалентно нанесению масштабной сетки на график Z(t), как показано на рис.1.4. Далее, в качестве пар значений
Рис. 1.4. Дискретизация аналогового сигнала за счет операций развертки по времени и квантования по величине
Ответом на эти сомнения служит так называемая теорема отсчетов, доказанная в 1933г. В. А. Котельниковым (по этой причине ее иногда называют его именем), значение которой для решения проблем передачи информации было осознано лишь в 1948г. после работ К. Шеннона. Теорема, которую примем без доказательства, но результаты будем в дальнейшем использовать, гласит:
Непрерывный сигнал можно полностью отобразить и точно воссоздать по последовательности измерений или отсчетов величины этого сигнала через одинаковые интервалы времени, меньшие или равные половине периода максимальной частоты, имеющейся в сигнале.
Комментарии к теореме:
Теорема касается только тех линий связи, в которых для передачи используются колебательные или волновые процессы.
Смысл теоремы в том, что дискретизация не приведет к потере информации и по дискретным сигналам можно будет полностью восстановить исходный аналоговый сигнал, если развертка по времени выполнена в соответствии со следующим соотношением:
Можно перефразировать теорему отсчетов:
Развертка по времени может быть осуществлена без потери информации, связанной с особенностями непрерывного (аналогового) сигнала, если шаг развертки не будет превышать Δt, определяемый в соответствии с (1.2).
Например, для точной передачи речевого сигнала с частотой до Vm = 4000 Гц при дискретной записи должно производиться не менее 8000 отсчетов в секунду; в телевизионном сигнале Vm ≈ 4 МГц, следовательно, для его точной передачи потребуется около 8000000 отсчетов в секунду.
Выбор шага развертки по времени и квантования по величине сигнала лежат в основе оцифровки звука и изображения. Примерами устройств, в которых происходят такие преобразования, являются сканер, модем, устройства для цифровой записи звука и изображения, лазерный проигрыватель, графопостроитель. Термины «цифровая запись», «цифровой сигнал» следует понимать как дискретное представление с применением двоичного цифрового алфавита.
Таким образом, преобразование сигналов типа N → D, как и обратное D → N, может осуществляться без потери, содержащейся в них информации.
Таким образом, за исключением N1 → N2 в остальных случаях оказывается возможным преобразование сообщений без потерь содержащейся в них информации. При этом на первый взгляд непрерывные и дискретные сообщения оказываются равноправными. Однако на самом деле это не так. Сохранение информации в преобразованиях N → D и D → N обеспечивается именно благодаря участию в них дискретного представления. Другими словами, преобразование сообщений без потерь информации возможно только в том случае, если хотя бы одно из них является дискретным. В этом проявляется несимметричность видов сообщений и преимущество дискретной формы. К другим ее достоинствам следует отнести:
• простоту и, как следствие, надежность и относительную дешевизну устройств по обработке информации;
• точность обработки информации, которая определяется количеством обрабатывающих элементов и не зависит от точности их изготовления;
Как называется сигнал параметры которого принимают конечное число значений
В предыдущем шаге было сказано, что передача информация производится с помощью сигналов, а самим сигналом является изменение некоторой характеристики носителя с течением времени. При этом в зависимости от особенностей изменения этой характеристики (т.е. параметра сигнала) с течением времени выделяют два типа сигналов: непрерывные и дискретные.
Если обозначить Z – значение параметра сигнала, а t – время, то зависимость Z(t) будет непрерывной функцией (рис.1(а)).
Рис.1. Непрерывные и дискретные сигналы
Примерами непрерывных сигналов являются речь и музыка, изображение, показание термометра (параметр сигнала – высота столба спирта или ртути – имеет непрерывный ряд значений) и пр.
Пример дискретных сигналов представлен на рис. 1(б). Как следует из определения, дискретные сигналы могут быть описаны дискретным и конечным множеством значений параметров
Принципиальным и важнейшим различием непрерывных и дискретных сигналов является то, что дискретные сигналы можно обозначить, т.е. приписать каждому из конечного числа возможных значений сигнала знак, который будет отличать данный сигнал от другого.
Природа знака может любой – жест, рисунок, буква, сигнал светофора, определенный звук и т.д. Природа знака определяется носителем сообщения и формой представления информации в сообщении.
Сами по себе знак или буква не несут никакого смыслового содержания. Однако такое содержание им может быть приписано – в этом случае знак будет называться символом. Например, силу в физике принято обозначать буквой F – следовательно, F является символом физической величины сила в формулах. Другим примером символов могут служить пиктограммы, обозначающие в компьютерных программах объекты или действия.
Таким образом, понятия «знак», «буква» и «символ» нельзя считать тождественными, хотя весьма часто различия между ними не проводят, поэтому в информатике существуют понятия «символьная переменная», «кодировка символов алфавита», «символьная информация» – во всех приведенных примерах вместо термина «символьный» корректнее было бы использовать «знаковый» или «буквенный».
Представляется важным еще раз подчеркнуть, что понятия знака и алфавита можно отнести только к дискретным сообщениям.