Как называют линию параметры которой равномерно распределены вдоль ее длины

5.1. Электрические цепи с распределенными параметрами основные определения

В этом разделе будем рассматривать длинные линии или цепи, сводящиеся к длинным линиям.

Электрическими линиями с распределенными параметрами назы­вают такие линии, в которых для одного и того же момента времени ток и напряжение непрерывно изменяются при переходе от одной точки (сечения) линии к другой, соседней точке.

Под магнитными линиями с распределенными параметрами пони­мают такие линии, магнитный поток и магнитное напряжение вдоль которых непрерывно меняются при переходе от одной точки линии к соседней.

Эффект непрерывного изменения тока (потока) и электрического (магнитного) напряжения вдоль линии существует вследствие того, что линии обладают распределенными продольными и поперечными сопротивлениями (рис. 5.1, а).

На схеме (рис. 5.1, а) изображен участок линии с распределен­ными параметрами, через dx обозначен бесконечно малый элемент длины линии.

В результате утечки тока через сопротивление Z ₄ ток . Аналогично, ток и т.д. Напряжение между точками а и b не равно напряжению между точками с и d и т.д.

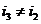
В электрических линиях с распределенными параметрами продоль­ные сопротивления образованы активными сопротивлениями проводов линии и индуктивностями двух противостоящих друг другу участков линии длиной dx. Поперечные сопротивления состоят из сопротивле­ний утечки, появляющейся вследствие несовершенства изоляции между проводами линии, и емкостей, образованных противостоящими друг другу элементами (участками) линии. В магнитных линиях с рас­пределенными параметрами продольные сопротивления представляют собой магнитные сопротивления самих магнитных стержней, образую­щих магнитную линию, а поперечные сопротивления обусловлены утечкой магнитного потока по воздуху между противостоящими друг

другу участками линии.

Линию с распределенными параметрами называют однородной, если равны друг другу все продольные сопротивления участков линии одинаковой длины и если равны друг другу все поперечные сопро­тивления участков линии одинаковой длины. Так, участок линии (рис. 5.1, а) однороден, если Z ₁ = Z ₂ = Z ₃ =… и Z ₄ = Z ₅ = Z ₆.

Линию с распределенными параметрами называют неоднородной, если продольные сопротивления в ней различны или поперечные сопротивления неодинаковы.

Кроме того, линии с распределенными параметрами можно под­разделить на две большие группы: нелинейные и линейные.

В качестве примера нелинейной электрической линии с распреде­ленными параметрами можно назвать электрическую линию передачи высокого напряжения при наличии между проводами линии тихого электрического разряда – явления короны на проводах. В этом слу­чае емкость между противостоящими друг другу участками линии является функцией напряжения между этими участками.

В качестве примера нелинейной магнитной линии с распределен­ными параметрами можно назвать линию, образованную параллельно расположенными магнитными сердечниками, которые в процессе работы линии могут насыщаться.

Когда говорят о линии с распределенными параметрами, то обычно этот термин мысленно связывают с мощными линиями передачи элек­трической энергии на большие расстояния, с телефонными и телеграф­ными воздушными или кабельными линиями, с рельсовыми линиями автоблокировки на железнодорожном транспорте, с антеннами в ра­диотехнике и другими родственными линиями и установками.

В то же время с линиями с распределенными параметрами имеют дело и тогда, когда «линий» в буквальном смысле слова, казалось бы, вовсе нет. Так, обычная индуктивная катушка при достаточно высо­ких частотах представляет собой линию с распределенными парамет­рами (рис. 5.1, б). Из рисунка (рис. 5.1, в) видно, что кроме индуктивностей в схеме замещения есть межвитковые емкости и емкости на корпус прибора (на землю).

Если по катушке проходит переменный ток, то через межвитко­вые емкости и емкости на землю также идет ток. При одном и том же напряжении между соседними витками ток через емкости тем больше, чем выше частота переменного тока. При низкой частоте (десятки, сотни, тысячи герц) ток через емкости несоизмеримо мал, по сравнению с токами через витки катушки, и наличие емкостей можно не учитывать в расчете (что и делалось до сих пор).

Если же частота тока очень велика, например сотни миллиардов герц, то токи через емкости могут во много раз превышать токи через витки катушки. В этом случае вся катушка в целом будет оказывать прохождению переменного тока емкостное, а не индуктивное сопротивление (коли­чественные изменения перешли в качественные).

При промежуточных частотах, порядка нескольких мегагерц (когда линейные размеры ка­тушки соизмеримы с длиной волны), индуктивная катушка является типичной линией с распределенными параметрами.

Если индуктивная катушка намотана на стальной сердечник, который способен насы­щаться, и частота тока достаточно велика, то все устройство в целом представляет собой сложную совокупность из электрической и маг­нитной нелинейных цепей с распределенными параметрами.

В курсе ТОЭ изучают только основы однородных линейных цепей с распределенными параметрами. Вся теория излагается применительно к электрическим линиям с распределенными параметрами на перемен­ном токе. Теория однородных линейных электрических цепей с рас­пределенными параметрами на постоянном токе непосредственно сле­дует из теории цепей переменного тока, если принять угловую частоту равной нулю.

Теория однородных линейных магнитных линий на постоянном токе в значительной мере аналогична теории однородных линейных электрических линий с распределенными параметрами, только вместо тока в уравнении должны быть подставлены:

Источник

Длинная линия. Примеры использования длинных линий. Основные параметры длинных линий

Длинная линия — электрическая линия, образованная двумя параллельными проводниками тока, длина которых превышает длину волны передаваемых электромагнитных колебаний, а расстояние между проводниками значительно меньше длины волны. Длинные линии, предназначенные для передачи электромагнитной энергии от передатчика к антенне или от антенны к входу приемника, называются фидерами. В зависимости от назначения длина фидерных линий может колебаться от единиц метров до десятков и даже сотен километров. В тоже время в радиотехнической практике широко используются сравнительно небольшие отрезки длинных линий.

Наиболее простым примером использования линий является открытый фидер, представляющий собой открытую линию, состоящую из двух параллельных (обычно медных) проводников. Расстояние между проводниками на всем протяжении линии неизменно благодаря применению опорных изоляторов, выполняемых из специальных высокочастотных керамических материалов. Первичные параметры и волновое сопротивление такого фидера определяются по формулам:

Единственное достоинство открытого фидера – его простота. Однако открытым фидерам присущ ряд серьезных недостатков, основным из которых является излучение фидером электромагнитной энергии вдоль всей его длины. Это излучение, резко возрастающее с укорочением длины волны, снижает коэффициент полезного действия и ухудшает диаграмму направленности антенны, питаемой таким фидером.
От основного недостатка, присущего открытой линии, свободна экранированная линия, выполняемая обычно в виде двухпроводного кабеля, в котором проводники разделены сплошным слоем твердого, но гибкого диэлектрика. Такая линия состоит из двух проводников, диэлектрика, экрана-оплетки из тонкой медной проволоки и защитной оболочки, выполняемой обычно из специальной пластмассы.
Благодаря применению экрана потери на излучение получаются весьма небольшими, однако с ростом частоты значительно возрастают диэлектрические потери, что ограничивает использование экранирование кабеля дециметровым диапазоном волн.

Рис. 4. Двухпроводная кабельная линия. Рис. 5. Коаксиальная линия.

С укорочением длины волны передаваемых вдоль фидера электромагнитных колебаний приходится отказываться от коаксиального кабеля, так как уже в дециметровом и тем более в сантиметровом диапазоне волн потери в нем резко возрастают. Потери в коаксиальной линии изменяются обратно пропорционально диаметрам проводников. Таким образом, преобладающим является затухание, связанное с наличием внутреннего проводника. Естественно поэтому стремление отказаться от внутреннего проводника и создать систему в виде полой трубы.
Такая труба, выполненная их хорошо проводящего материала и являющаяся граничной поверхностью для электромагнитных волн, называется волноводом. Волноводы представляют собой особый тип длинных линий.
Разомкнутые и короткозамкнутые отрезки длинных линий обладают свойствами настроенных контуров. Аналогичные свойства имеют и отрезки волноводов, замкнутые на обоих концах. Такие колебательные системы, называемые объемными резонаторами, широко применяются в диапазоне сантиметровых волн, где не только обычные колебательные контуры с сосредоточенными параметрами, но и отрезки длинных линий становятся уже практически неприменимыми из-за больших потерь.

Процессы, протекающие в длинной линии при передаче электромагнитной энергии, можно представить следующим образом: при подключении генератора к входным зажимам линии между проводами возникает электрическое поле, которое создает движение электронов, сопровождаемое появлением магнитного поля. Следовательно, напряжение и ток в линии связаны с существованием электромагнитного поля, силовые линии которого окружают проводники. В движущемся электромагнитном поле и заключена передаваемая вдоль линии энергия.

Всякая длинная линия имеет распределенные по длине индуктивность L, емкость между проводами С, активное сопротивление R и активную проводимость между проводами G, наличие которой обусловлено несовершенством изоляции.

Если параметры линии равномерно распределены по длине, то обозначая соответствующие величины на единицу длины через L₁,C₁,R₁ и G₁, имеем для линии длиной l.

Коэффициент Zc называют волновым сопротивление линии, а α – фазовой постоянной, причем λ – длина волны колебаний, передаваемых вдоль линии. Иногда величины α и Zc называют вторичными параметрами линии.

Длинная линия называется однородной, если значения её параметров неизменны на всём протяжении. При отсутствии в линии электрических потерь, т. е. R = G = 0 (обычно на радиочастотах):

Длинные линии применяют для передачи информации в дальней телеграфно-телефонной связи, телевидении, радиолокации, а также для передачи энергии по проводам на далёкие расстояния

Источник

Методы определения МП.

Импульсные методы ОМП.

Понятие о линиях с распределенными параметрами.

Фактически параметры электрической цепи всегда распределены вдоль ее участков. Но во многих случаях можно без заметной погрешности считать, что активное и реактивное сопротивления сосредоточены в определенных точках цепи. Такое допущение справедливо, когда скорость изменения во времени напряжений и токов пренебрежимо мала по сравнению со скоростью распространения электромагнитной волны вдоль цепи. При периодических токах и напряжениях это условие означает, что волна успевает пробежать вдоль всей линии за небольшую долю периода. Если же за время пробега волны от начала до конца цепи (или обратно) токи и напряжения успевают заметно измениться, то такую цепь называют линией с распределенными параметрами, или длинной линией.

Очевидно, что токи и напряжения в таких линиях являются функциями двух параметров: времени t и длины линии 1. При этом длина волны Л определяется формулой

Линию, параметры которой распределены равномерно по ее длине, называют однородной. Сюда относятся, в частности, участки ВЛ и КЛ, на всем протяжении которых сечение непрерывных проводников, их взаимное расположение и характеристики среды не изменяются. В точках нарушения однородности (место повреждения, разветвления, транспозиции, соединительная муфта), называемых также особыми точками, возникают отраженные (движущиеся в обратном направлении) и преломленные волны. Отраженная волна возвращается к месту посылки сигнала, и по времени двойного пробега ее можно судить о расстоянии до МП.

Значение синусоидального сигнала в данной точке линии является синусоидальной функцией времени, а в каждый данный момент оно будет распределено вдоль линии также по синусоидальному закону. Такая волна напряжения перемещается по линии с постоянной скоростью v и называется бегущей волной. Из-за наличия активных потерь по мере продвижения вдоль линии волна затухает по показательному закону (рис. 5.12). Волны, бегущие от начала линии к ее концу, называются прямыми, или падающими, в обратном направлении — обратными, или отраженными. Каждое значение бегущей волны в данной точке линии представляет собой сумму прямой и обратной волн. В частном случае одной из волн может и не быть.

Рис.5.12. Бегущая волна в линии с потерями

Источник

Установившиеся режимы в электрических цепях с распределенными параметрами

Определение цепей с распределенными параметрами. Упрощенная теория линий

В цепях с распределенными параметрами электрическое, магнитное поля и потери энергии распределены вдоль участков цепи, а напряжения и токи различны для разных точек (сечений) цепи. Примеры цепей с распределенными параметрами: длинные линии электропередачи, линии электропроводной связи и телеуправления, обмотки трансформаторов и электрических машин и др.

Если расстояние между проводами длинной линии много меньше длины волны электромагнитных колебаний между проводами, то для расчета такой линии применима упрощенная теория, которая основана на понятиях теории электрических цепей (напряжения, токи, сопротивления, индуктивности, емкости), а не на теории электромагнитного поля, которая учитывает, что электрическое и магнитное поля линии распределяются внутри проводов и между проводами. Ниже излагается упрощенная теория.

Дифференциальные уравнения однородной линии и их решение для синусоидального режима

Линия, параметры которой равномерно распределены вдоль всей ее длины, называется однородной.

Рассмотрим однородную двухпроводную линию с индуктивностью Цу1х, активным сопротивлением R_Qdx, емкостью 131

Каждый элементарный участок линии можно рассматривать как элементарный четырехполюсник, а линию в целом можно считать симметричным пассивным четырехполюсником относительно любых двух сечений, например относительно входных и выходных зажимов.

По законам Кирхгофа

После упрощения последних уравнений, сократив их на dx, получим систему основных дифференциальных уравнений линии с распределенными параметрами

Будем полагать, что в линии установившийся режим при синусоидальном напряжении источника питания. Уравнения (9.1) и (9.2) в комплексной форме

Источник

Линия (единица длины)

В старорусской системе мер 1 линия = 1⁄16 ногтя = 1⁄256 пяди = 0,69453 мм.

В русской (с XVIII века) и английской системах мер 1 линия («большая») = 1⁄10 дюйма = 10 точек = 2,54 мм.

В английской системе мер 1 линия («малая») = 1⁄12 дюйма = 2,11666666… мм. Эта единица использовалась редко, так как в технике использовались десятые, сотые и тысячные («милы») доли дюйма. Измерения в биологии и типографском деле использовали эту единицу, сокращая её как ” (за пределами этих областей линию обозначали как ”’, a ” применялось и применяется для обозначения дюйма).

Изготовители пуговиц для измерения толщины пуговиц использовали специальную линию, равную 1⁄40 дюйма = 0,635 мм, также известную как англ. button measure.

«Французская» линия = 1⁄144 «нормального фута» = 2,255 мм.

* В новопольской и прусской системах мер линия составляла 2,0 и 2,17 мм соответственно.

Связанные понятия

Шичжи (кит. упр. 市制, пиньинь: shìzhì — «рыночная система») — система мер, имевшая употребление в Китае до конца XX века. В КНР меры были стандартизированы для соответствия Международной системе единиц (СИ), а древняя система мер имела в основании число 16. В Гонконге английская система мер использовалась вместе с гонконгской, а с 1976 года к употребимым единицам добавились метрические. Тайваньская система мер использовалась под японским и голландским владычеством, в ней многие одноимённые меры обладали.

Упоминания в литературе

Связанные понятия (продолжение)

Идеи, сходные с теми, которые лежат в основании метрической системы, обсуждались в XVI и XVII столетиях. Симон Стевин опубликовал предложения по десятичной записи, а Джон Уилкинс опубликовал проект десятичной системы мер, основанной на естественных единицах. Первую практическую реализацию метрической системы осуществили в 1799 году, во время Великой Французской революции, когда существовавшая система мер, которая приобрела дурную репутацию, была временно заменена десятичной системой, основанной на.

Сякканхо́ (яп. 尺貫法 сякканхо:) — традиционная японская система мер длины, объёма, площади, веса и денег, которая частично происходит от китайской, распространённой ранее во всей Восточной Азии.

В европейской традиции исторически сложились два варианта построения системы наименования чисел.

Эта статья содержит два списка стран по длине береговой линии в километрах. Если это значение равно нулю, значит страна не имеет выхода к морю.

Источник