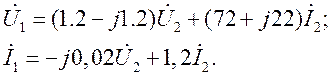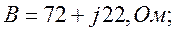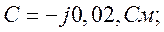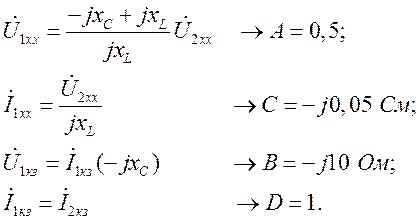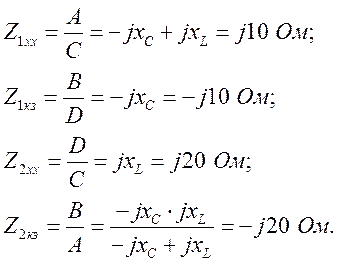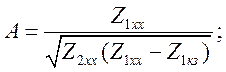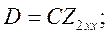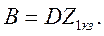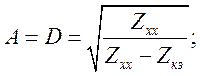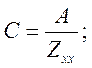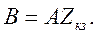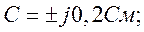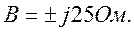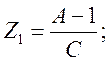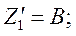Как определить а параметры четырехполюсника

1.4 Способы определения параметров четырехполюсника

Параметры четырехполюсника могут быть определены или расчетным путем по его внутренней схеме, или по результатам измерений с помощью измерительных приборов: вольтметра, амперметра, ваттметра или фазометра.

По известной внутренней схеме четырехполюсника его параметры можно определить различными способами:

а) составлением уравнений по законам Кирхгофа (либо методом контурных токов или узловых напряжений) и представлением их решения в виде одной из форм уравнений;

б) по значениям напряжений и токов в режимах холостого хода и короткого замыкания;

в) по входным сопротивлениям в режимах холостого хода и короткого замыкания;

г) разбивкой сложного четырехполюсника на более простые четырехполюсники, параметры которых известны.

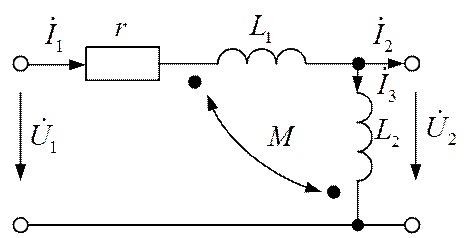
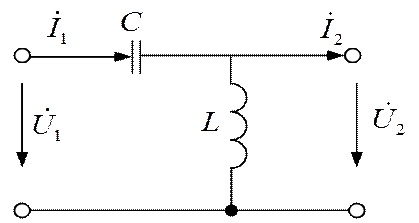
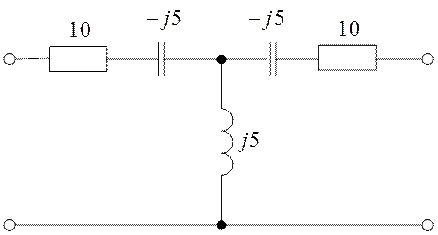
Определить коэффициенты матрицы [А] для четырехполюсника (рис. 1.2) при заданных параметрах схемы: r = 60 Ом; ωL₁ = 20 Ом; ωL₂ = 60 Ом;
ωM = 10 Ом.

Из системы уравнений по законам Кирхгофа:

(1.12)

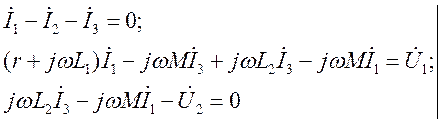
исключением тока 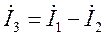и приведением (1.12) к виду (1.9) получим:

Следовательно, .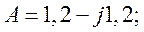

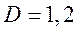
Определить коэффициенты матрицы [А] двумя способами:

а) из уравнений Кирхгофа для режимов холостого хода и короткого замыкания;

б) через входные сопротивления холостого хода и короткого замыкания.

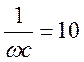
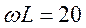
Параметры схемы: Ом, Ом.

А. Из уравнений Кирхгофа для режимов холостого хода и короткого замыкания:

, (1.13)

, (1.14)

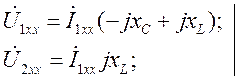
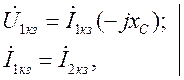
Б. Входные сопротивления холостого хода и короткого замыкания со стороны входных зажимов:

Выбирая три сопротивления из четырех и дополняя уравнением (1.10), находим

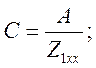
Получили матрицу .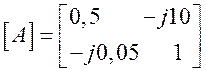

Для симметричного четырехполюсника в результате измерений получены значения сопротивлений: Z_xx=10 Ом; Z_кз=12,5 Ом.

Определить А – параметры четырехполюсника.

Для симметричного четырехполюсника

Получаем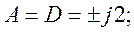

Следовательно, данным измерений соответствуют две матрицы:

и (1.13)

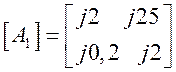
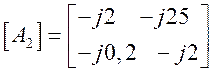
и два эквивалентных четырехполюсника.

1.5. Схемы замещения четырехполюсника

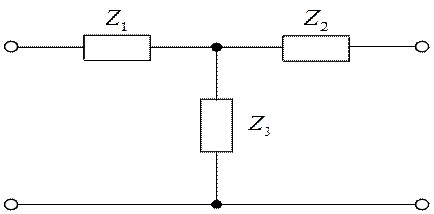
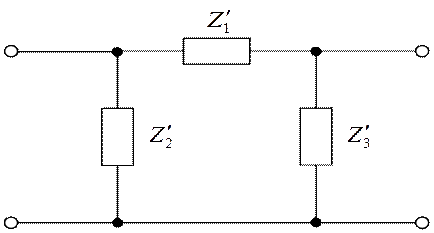
Каждый пассивный четырехполюсник с известными параметрами одной из форм может быть представлен схемой замещения с минимальным числом элементов. Так как только три параметра четырехполюсника являются независимыми, то и минимальное число элементов в схеме замещения, отвечающих этим параметрам, равно трем. Такими простейшими схемами замещения являются Т – образная и П – образная (рис. 1.4).

Рис. 1.4. а) Т – образная схема; б) П – образная схема

Матрица [А]_Т – для Т – образной схемы легко определяется из уравнений для контурных токов и имеет вид

. (1.14)

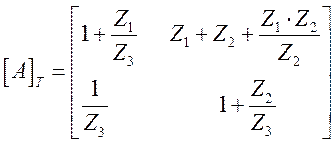
Матрица [А]_П – для П – образной схемы находится из уравнений, составленных по методу узловых потенциалов и имеет вид:

. (1.15)

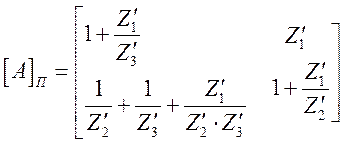
Параметры схем замещения определяются через коэффициенты матриц [А]_Т и [А]_П :

– для Т – образной схемы:

(1.16)

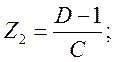
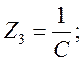
– для П – образной схемы:

(1.17)

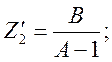
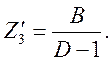
Определить параметры Т – образных схем замещения четырехполюсника по матрицам [А₁] и [А₂] примера 1.3.

Используя соотношения (1.16), находим параметры двух схем замещения, изображенных на рис. 1.5.

Рис. 1.5 Две эквивалентные схемы замещения

Используя выражение (1.7), находим:

Чтобы распечатать файл, скачайте его (в формате Word).

Источник

Определить А-параметры четырехполюсника

Аналитические отношения токи и напряжения на входе и на выходе четырехполюсника называются уравнениями передачи четырехполюсника. Величины связывающие токи и напряжения в этих уравнениях называют параметрами четырехполюсника.

В системе уравнений с А-параметрами ток и напряжение на зажимах определяются через ток и напряжение на выходных зажимах.

Запишем уравнения А-параметров для четырехполюсника:

Расчет эквивалентных сопротивлений данного четырехполюсника

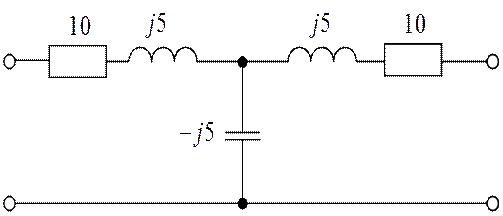
Рис. 1.1.1 Схема четырехполюсника, данная по условию

Для этого рассчитаем комплексное сопротивление индуктивности для заданной циклической частоты щ =1499 рад/с:

Рис. 1.1.2 Схема четырехполюсника, данная по условию, с присвоенными индексами Z

Расчет А-параметров четырехполюсника методом холостого хода и короткого замыкания

Рис. 1.2.1 Схема четырехполюсника при холостом ходе

Учитывая это, преобразуем уравнения А-параметров четырехполюсника (стр.6 1.1):

Рассчитаем по полученным формулам (1.2.2; 1.2.3) А-параметры:

Рис. 1.2.2 Схема четырехполюсника при коротком замыкании

Выразим параметры из уравнений (1.2.4) и

Рассчитаем эти параметры с помощью полученных выражений (1.2.7; 1.2.8)

Для проверки правильности расчетов А-параметров применим правило: определитель матрицы А-параметров обратимого четырехполюсника должен быть равен 1.

Матрица А-параметров имеет вид (1.3.1):

Составим выражение для нахождения ее определителя (1.3.2)

Рассчитаем определитель матрицы А-параметров данного четырехполюсника:

Определитель матрицы составленной из А-параметров четырехполюсника равен 1, следовательно расчет А-параметров произведен верно.

Источник

Термины и определения основных понятий

Электрическая цепь имеющая два входных и два выходных зажима называется четырехполюсником.

Активные ЧП содержит внутри себя источники электрической энергии. Пассивные ЧП не содержит источники электрической энергии. В дальнейшем рассматриваем только пассивные ЧП.

Примерами ЧП могут служить: линия передачи, трансформатор, электрический фильтр и т. д.

Выводы ЧП к которым подключается источник электрической энергии называются входными, а выводы, к которым присоединяется нагрузка – выходными.

ЧП называется симметричным, если перемена местами его входных и выходных зажимов не изменяет напряжение и ток в остальной части цепи куда он подключен. В противном случае ЧП называется несимметричным.

На рисунке приведена в общем виде схема ЧП. Принятому положительному направлению токов соответствует передача энергии от входных зажимов к выходным зажимам.

Соотношение между напряжениями и токами могут быть записаны в виде следующих уравнений:

1.Форма || Y ||

Здесь все Y –комплексные коэффициенты пропорциональности, имеющие размерность проводимости.

При этом:

2.Форма || Z ||

При этом :

3.Форма ||А||

При этом справедливо:

Наличие связи между коэффициентами, а также ;

показывает, что при любой форме записи уравнений ЧП независимыми являются только 3 параметра.

Коэффициенты зависят от схемы внутренних соединений ЧП, от величины сопротивлений схемы и частоты.

Если поменять местами вход и выход ЧП, то

Для симметричного ЧП:

Определение коэффициентов ЧП ( первичных параметров)

Если внутреннее содержимое ЧП известно, то его коэффициенты можно определить теоретически (расчетным путем).

1 способ. Он состоит в записи уравнений по законам Кирхгофа и последовательным приведением этих уравнений к одной из форм уравнений .

(1)

Приведем полученную систему к форме || Z ||:

Из (3): подставим с в (1) и (2)

форма ||Z||

Приведем полученную систему к форме || A ||:

Из (2)

— верно

2 способ: По известным напряжениям и токам в режимах холостого хода и короткого замыкания.

Покажем, что этим способом мы получили те же результаты:

Величина входного сопротивления могут быть легко найдена с помощью амперметра, вольтметра и ваттметра.

Для входных зажимов ЧП входное сопротивление:

При ХХ () (1)

При КЗ () (2)

Еще одно уравнение получим из уравнений для обратного включения.

Для обратного включения имеем:

В режиме ОКЗ () (3)

Решим уравнения (1)—(3) относительно какого-либо коэффициента (например А). Для этого выразим коэффициенты В, С, D и подставим полученные значения в уравнение связи.

Для симметричного ЧП A = D и

Поэтому

Для определения коэффициентов симметричного ЧП достаточно провести опыты ХХ и КЗ.

Эквивалентные схемы ЧП.

Т. К.пассивный ЧП характеризуется тремя независимыми параметрами, то его эквивалентная схема должна содержать как минимум три элемента.

На рисунке привидены Т и П-образная эквивалентные схемы.

Выразим Т-схемы через .

Тогда

Или

Аналогично для П-схемы имеем:

Пассивный ЧП не содержит источников электрической энергии, активные – содержат.

Примеры ЧП: линия передачи, трансформатор, электрический фильтр и т. д.

Выводы ЧП к которым подключается источник электрической энергии называются входными, а выводы с нагрузкой – выходными.

ЧП называется симметричным если перемена местами его входных и выходных зажимов не изменяет напряжение и ток в остальной части цепи куда он подключен.

Соотношение между напряжениями и токами ЧП могут быть записаны в виде следующих уравнений:

Здесь все Y –комплексные коэффициенты пропорциональности имеющие размерность проводимости.

Если поменять входное и выходное, то

Определение коэффициентов ЧП

Если внутреннее содержимое ЧП известно, то его коэффициенты можно определить аналитически.

I.

C остоит в записи уравнений по законам Кирхгофа и последовательным приведением этих уравнений к одной из форм уравнений ЧП.

Входное сопротивление R со стороны вторичных зажимов.

Величины входных сопротивлений находятся с помощью А, В и Вг

Эквивалентные схемы ЧП.

Так как пассивный ЧП характеризуется тремя независимыми параметрами, то его эквивалентная схема должна содержать как минимум тир элемента.

Широкое распространение получили Т и П-образные схемы.

Величины входных сопротивлений находятся с помощью амперметра, вольтметра и ваттметра.

1. Что такое четырехполюсник?

2. Что такое активный четырехполюсник?

3. Что такое пассивный четырехполюсник?

4. Приведите примеры четырехполюсников.

5. Какие четырехполюсники называются входными, а какие – выходными?

6. Какие четырехполюсники называются симметричными, а какие – несимметричными?

7. Опишите 3 способа определении коэффициентов четырехполюсников

8. Какие существуют схемы замещения четырехполюсников?

Упражнения и задачи

1. Определить А-параметры четырехполюсника:

а) используя законы Кирхгофа; б) при режимах холостого хода и короткого замыкания.

Источник