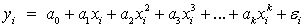Как оценивается значимость параметров уравнения регрессии
Оценка значимости уравнения регрессии. Коэффициент детерминации
Проверить значимость уравнения регрессии — значит установить, соответствует ли математическая модель, выражающая зависимость между переменными, экспериментальным данным и достаточно ли включенных в уравнение объясняющих переменных (одной или нескольких) для описания зависимой переменной.
Проверка значимости уравнения регрессии производится на основе дисперсионного анализа.
В математической статистике дисперсионный анализ рассмотрен как самостоятельный инструмент (метод) статистического анализа.
Здесь же он применяется как вспомогательное средство для изучения качества регрессионной модели.
Согласно основной идее дисперсионного анализа (см., § 2.9)
Убедимся в том, что пропущенное в (3.41) третье слагаемое
/=1 
(с учетом соотношения (3.31)).
Схема дисперсионного анализа имеет вид, представленный в табл. 3.3.
Число степеней свободы
Средние квадраты и s (табл. 3.3) представляют собой несмещенные оценки дисперсий зависимой переменной, обусловленных соответственно регрессий или объясняющей переменной X и воздействием неучтенных случайных факторов и ошибок; т — число оцениваемых параметров уравнения регрессии; п — число наблюдений.
Замечание. При расчете общей суммы квадратов Q полезно иметь в виду, что
При отсутствии линейной зависимости между зависимой и объясняющими(ей) переменными случайные величины s r = Qr /( т
О и s 1= Qe/(n—m) имеют /^-распределение соответственно с т— 1 и п
т степенями свободы, а их отношение — ^-распределение с теми же степенями свободы (см. § 2.3). Поэтому уравнение регрессии значимо на уровне а, если фактически наблюдаемое значение статистики
где Fa.*,.*2 — табличное значение /’-критерия Фишера—
Снедекора, определенное на уровне значимости а при к=т
и ki=n—m степенях свободы.
В случае линейной парной регрессии т = 2, и уравнение регрессии значимо на уровне а, если
Следует отметить, что значимость уравнения парной линейной регрессии может быть проведена и другим способом, если оценить значимость коэффициента регрессии Ь, который, как отмечено в § 3.4. имеет /-распределение Стьюдента с к—п—2 степенями свободы.
Уравнение парной линейной регрессии или коэффициент регрессии Ь значимы на уровне а (иначе — гипотеза #о о равенстве параметра Pi нулю, т. е. Я0: Pi=0, отвергается), если фактически наблюдаемое значение статистики (3.37)
больше критического (по абсолютной величине), т. е.
В ряде прикладных задач требуется оценить значимость коэффициента корреляции г (§ 3.3). При этом исходят из того, что
имеет /-распределение Стьюдента с п — 2 степенями свободы.
Коэффициент корреляции г значим на уровне а (иначе — гипотеза Я0 о равенстве генерального коэффициента корреляции р нулю, т. е. Но: р=0, отвергается), если
где /|_а;„_2— табличное значение /-критерия Стьюдента, определенное на уровне значимости а при числе степеней свободы п— 2.
Легко показать, что получаемые значения /-критерия для проверки гипотез р=0 по (3.45) и р=0 по (3.46) одинаковы.
По данным табл. 3.1 оценить на уровне а=0,05 значимость уравнения регрессии У по X
Решение. 1-й способ. Выше, в примерах 3.1, 3.2 были 10 10
Вычислим необходимые суммы квадратов по формулам (3.40), (3.42):
По таблице /^распределения (табл. IV приложений) /o.o5;i;8 = 4,20. Так как />/Ь,о5;1;8> то Уравнение регрессии значимо.
2-й способ. Учитывая, что />i = l,016, ^(jc, -х) = 24,40,
s 2 = 1,049 (см. пример 3.3, табл. 3.2), по формуле (3.45)
говорят, мерой качества подгонки регрессионной модели к наблюденным значениям уд, характеристикой прогностической силы анализируемой регрессионной модели является коэффициент детерминации, определяемый по формуле
Величина R 2 показывает, какая часть (доля) вариации зависимой переменной обусловлена вариацией объясняющей переменной.
Так как 0 2 2 к единице, тем лучше регрессия аппроксимирует эмпирические данные, тем теснее наблюдения примыкают к линии регрессии. Если R 2 = 1, то эмпирические точки (х,, уд лежат на линии регрессии (см. рис. 3.3) и между переменными Y и X существует линейная функциональная зависимость. Если R 2 = 0, то вариация зависимой переменной полностью обусловлена воздействием неучтенных в модели переменных, и линия регрессии параллельна оси абсцисс (см. рис. 3.4).
Заметим, что коэффициент R 2 имеет смысл рассматривать только при наличии свободного члена в уравнении регрессии, так как лишь в этом случае, как уже отмечалось, верно равенство (3.41), а следовательно, и (3.47).
По данным табл. 3.1 найти коэффициент детерминации и пояснить его смысл.
Решение. В примере 3.4 было получено Qr =25,21, 0= 33,6.
По формуле (3.47) R 2 =^- = ^^- = 0,750. (Коэффициент
детерминации можно было вычислить и иначе, если учесть, что в примере 3.2 был вычислен коэффициент корреляции /-0,866. Тогда Д 2 =Я=0,866 2 =0,750.)
Как оценивается значимость параметров уравнения регрессии?



Оценка знач-ти Ур-я в целом дается с помощью F-критерия
Фишера: выдвигается гипотеза, что коэф-нт регрессии =0 (b=0) след-но Xне оказ-т влияние на Y. Расч F-критерия предшест-т анализ дисперсии. Дел-ся разд-е общей ∑ квадратов откл-й перем-й Y от средн знач Y на 2 части – «объясненную и необъясненную»: ∑(Yi-Yср)2= ∑(Yтеор(X1)-Yср)2
+∑(Yтеор(Xi)-Yi)2, те общей ∑ квадратов откл-й=∑
квадратов отклонений(объясненная регрессия)+остаточная ∑квадратов
отклонений. Общ ∑ квадратов отклонений инд-х знач от ср знач вызвана
влиянием множества причин. Если нет влияния рассматриваемого фактора, то линия
регрессии парал-на оси OX, остаточная ∑квадратов отклонений озн-т проч и
неучт-е фак-ры. ∑ квадратов откл-й связана с числом степеней
свободы(Degrees of freedom) – это число независимо варьирующих признаков,
влияющих на соотв ∑ квадратов откл-й. Общ ∑ квадратов откл-й имеет
число степеней свободы (n-1). Yср=(Y1+Yn)/n. Для остаточн ∑квадратов
отклонений число степеней свободы= (n-2). Если соотв ∑квадратов
отклонений разделить на соотв ∑ степеней свободы, то получится
дисперсия(D) на 1 степень свободы. ∑квадратов отклонений объясн регрессии
– число степеней свободы=1. Dобщ=∑(Y-Yср)2/( n-1),
/(n-2). Fкритерий Фишера F=Dфакт/Dост. Если гипотеза справедлива, то
Dфакторн=Dост, но для гипот-зы необх опроверж этого, те Dфакт>Dост. Есть
таблицы крит-х знач Fкритерий-это макс вел-на отношения дисперсии для дан
уровня вероят-ти. Если Fфакт> Fтабл, то Ур-е регрессии явл-ся значимым
(гипотеза отклоняется) и наоборот(гипотеза не может отклониться без
существенного риска). Можно говорить о значимости не только Ур-я вцелом, но и
его параметров. Для этого опр-ся их станд-я ошибка. Yтеор=a(альфа)+b(бетта)*xi.
Ma- ср квадр откл-е а от альфы и Mb-соотв. Tфактор=a/Mа>табл, то явл-ся
знач-м. Ma=корень квадратный из ∑(Yтеор(Xi)-Yi)2/(n-2)*
∑x2/[n*∑(x-xср)2]; Mb=корень квадратный из
∑(Yтеор(Xi)-Yi)2=Sост в квадрате
Коэф-т Мb* определяет наклон прямой регрессии.
8.Запишите все виды моделей, нелинейных относительно:
– объясняющих переменных;
– оцениваемых параметров.
Если между экономическими явлениями существуют нелинейные соотношения, то они выражаются с помощью соответствующих нелинейных функций.
Различают два класса нелинейных регрессий:
регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам: регрессии, нелинейные по оцениваемым параметрам.
Нелинейные регрессии по включаемым в нее объясняющим переменным, но линейные по оцениваемым параметрам
Данный класс нелинейных регрессий включает уравнения, в которых зависимая переменная линейно связана с параметрами. Примером могут служить: полиномы разных степеней
и равносторонняя гипербола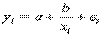
Полином любого порядка сводится к линейной регрессии с ее методами оценивания параметров и проверки гипотез.
Среди нелинейной полиноминальной регрессии чаще всего используется парабола второй степени; в отдельных случаях — полином третьего порядка. Ограничение в использовании полиномов более высоких степеней связаны с требованием однородности исследуемой совокупности: чем выше порядок полинома, тем больше изгибов имеет кривая и, соответственно, менее однородна совокупность по результативному признаку.
Равносторонняя гипербола, для оценки параметров которой используется тот же подход «замены переменных» (1/x заменяют на переменную z) хорошо известна в эконометрике.
Она может быть использована, например, для характеристики связи удельных расходов сырья, материалов и топлива с объемом выпускаемой продукции. Также примером использования равносторонней гиперболы являются кривые Филлипса и Энгеля..
Пример нахождения статистической значимости коэффициентов регрессии
Связь между признаком Y фактором X сильная и прямая
Уравнение регрессии
Анализ точности определения оценок коэффициентов регрессии
S a = 0.2704
Доверительные интервалы для зависимой переменной
Рассчитаем границы интервала, в котором будет сосредоточено 95% возможных значений Y при неограниченно большом числе наблюдений и X = 88,16
(128.06;163.97)
Проверка гипотез относительно коэффициентов линейного уравнения регрессии
1) t-статистика
Статистическая значимость коэффициента регрессии a подтверждается
Fkp = 4.96
Поскольку F > Fkp, то коэффициент детерминации статистически значим.
Коэффициент корреляции
Рассчитываем показатель тесноты связи. Таким показателем является выборочный линейный коэффициент корреляции, который рассчитывается по формуле:
Т.е. увеличение x на величину среднеквадратического отклонения этого показателя приведет к увеличению средней среднедневной заработной платы Y на 0.721 среднеквадратичного отклонения этого показателя.
1.4. Ошибка аппроксимации.
Оценим качество уравнения регрессии с помощью ошибки абсолютной аппроксимации.
2.3. Анализ точности определения оценок коэффициентов регрессии.
Несмещенной оценкой дисперсии возмущений является величина:
2.4. Доверительные интервалы для зависимой переменной.
Экономическое прогнозирование на основе построенной модели предполагает, что сохраняются ранее существовавшие взаимосвязи переменных и на период упреждения.
Для прогнозирования зависимой переменной результативного признака необходимо знать прогнозные значения всех входящих в модель факторов.
Прогнозные значения факторов подставляют в модель и получают точечные прогнозные оценки изучаемого показателя.
(a + bxp ± ε)
где
Рассчитаем границы интервала, в котором будет сосредоточено 95% возможных значений Y при неограниченно большом числе наблюдений и X p = 94
(76.98 + 0.92*94 ± 7.8288)
(155.67;171.33)
С вероятностью 95% можно гарантировать, что значения Y при неограниченно большом числе наблюдений не выйдет за пределы найденных интервалов.
2.5. Проверка гипотез относительно коэффициентов линейного уравнения регрессии.
1) t-статистика. Критерий Стьюдента.
Проверим гипотезу H0 о равенстве отдельных коэффициентов регрессии нулю (при альтернативе H1 не равно) на уровне значимости α=0.05.
tкрит = (10;0.05) = 1.812
Поскольку 3.2906 > 1.812, то статистическая значимость коэффициента регрессии b подтверждается (отвергаем гипотезу о равенстве нулю этого коэффициента).
где m – число факторов в модели.
Оценка статистической значимости парной линейной регрессии производится по следующему алгоритму:
1. Выдвигается нулевая гипотеза о том, что уравнение в целом статистически незначимо: H0: R 2 =0 на уровне значимости α.
2. Далее определяют фактическое значение F-критерия:
где m=1 для парной регрессии.
3. Табличное значение определяется по таблицам распределения Фишера для заданного уровня значимости, принимая во внимание, что число степеней свободы для общей суммы квадратов (большей дисперсии) равно 1 и число степеней свободы остаточной суммы квадратов (меньшей дисперсии) при линейной регрессии равно n-2.
4. Если фактическое значение F-критерия меньше табличного, то говорят, что нет основания отклонять нулевую гипотезу.
В противном случае, нулевая гипотеза отклоняется и с вероятностью (1-α) принимается альтернативная гипотеза о статистической значимости уравнения в целом.
Табличное значение критерия со степенями свободы k1=1 и k2=10, Fkp = 4.96
Поскольку фактическое значение F > Fkp, то коэффициент детерминации статистически значим (Найденная оценка уравнения регрессии статистически надежна).
Оценка параметров уравнения регреcсии. Пример
Задание:
По группе предприятий, выпускающих один и тот же вид продукции, рассматриваются функции издержек:
y = α + βx;
y = α x β ;
y = α β x ;
y = α + β / x;
где y – затраты на производство, тыс. д. е.
x – выпуск продукции, тыс. ед.
1. Уравнение имеет вид y = α + βx
1. Параметры уравнения регрессии.
Средние значения
Связь между признаком Y фактором X сильная и прямая
Уравнение регрессии
| x | y | x 2 | y 2 | x ∙ y | y(x) | (y- y ) 2 | (y-y(x)) 2 | (x-x p ) 2 |
| 78 | 133 | 6084 | 17689 | 10374 | 142.16 | 115.98 | 83.83 | 1 |
| 82 | 148 | 6724 | 21904 | 12136 | 148.61 | 17.9 | 0.37 | 9 |
| 87 | 134 | 7569 | 17956 | 11658 | 156.68 | 95.44 | 514.26 | 64 |
| 79 | 154 | 6241 | 23716 | 12166 | 143.77 | 104.67 | 104.67 | 0 |
| 89 | 162 | 7921 | 26244 | 14418 | 159.9 | 332.36 | 4.39 | 100 |
| 106 | 195 | 11236 | 38025 | 20670 | 187.33 | 2624.59 | 58.76 | 729 |
| 67 | 139 | 4489 | 19321 | 9313 | 124.41 | 22.75 | 212.95 | 144 |
| 88 | 158 | 7744 | 24964 | 13904 | 158.29 | 202.51 | 0.08 | 81 |
| 73 | 152 | 5329 | 23104 | 11096 | 134.09 | 67.75 | 320.84 | 36 |
| 87 | 162 | 7569 | 26244 | 14094 | 156.68 | 332.36 | 28.33 | 64 |
| 76 | 159 | 5776 | 25281 | 12084 | 138.93 | 231.98 | 402.86 | 9 |
| 115 | 173 | 13225 | 29929 | 19895 | 201.86 | 854.44 | 832.66 | 1296 |
| 0 | 0 | 0 | 16.3 | 20669.59 | 265.73 | 6241 | ||
| 1027 | 1869 | 89907 | 294377 | 161808 | 1869 | 25672.31 | 2829.74 | 8774 |
2. Оценка параметров уравнения регрессии
Значимость коэффициента корреляции
Анализ точности определения оценок коэффициентов регрессии
S a = 0.1712
Доверительные интервалы для зависимой переменной
Рассчитаем границы интервала, в котором будет сосредоточено 95% возможных значений Y при неограниченно большом числе наблюдений и X = 1
(-20.41;56.24)
Проверка гипотез относительно коэффициентов линейного уравнения регрессии
1) t-статистика
Статистическая значимость коэффициента регрессии a подтверждается
Fkp = 4.84
Поскольку F > Fkp, то коэффициент детерминации статистически значим
Оценка значимости параметров уравнения регрессии
Оценка значимости параметров уравнения линейной регрессии производится с помощью критерия Стьюдента:
если tрасч. > tкр, то принимается основная гипотеза (Ho), свидетельствующая о статистической значимости параметров регрессии;
Вопросы для самопроверки по 2 разделу
1. Укажите основные составляющие эконометрической модели и их сущность.
2. Основное содержание этапов эконометрического исследования.
3. Сущность подходов по определению параметров линейной регрессии.
4. Сущность и особенность применения метода наименьших квадратов при определении параметров уравнения регрессии.
5. Какие показатели используются для оценки тесноты взаимосвязи исследуемых факторов?
6. Сущность линейного коэффициента корреляции.
7. Сущность коэффициента детерминации.
8. Сущность и основные особенности процедур оценки адекватности (статистической значимости) регрессионных моделей.
9. Оценка адекватности линейных регрессионных моделей по коэффициенту аппроксимации.
10. Сущность подхода оценки адекватности регрессионных моделей по критерию Фишера. Определение эмпирических и критических значений критерия.
11. Сущность понятия «дисперсионный анализ» применительно к эконометрическим исследованиям.
12. Сущность и основные особенности процедуры оценки значимости параметров линейного уравнения регрессии.
13. Особенности применения распределения Стьюдента при оценке значимости параметров линейного уравнения регрессии.
14. В чем состоит задача прогноза единичных значений исследуемого социально-экономического явления?
Содержание практического занятия № 2.1 «Метод наименьших квадратов. Определение параметров линейного уравнения регрессии»:
1. Построить поле корреляции и сформулировать предположение о форме уравнения взаимосвязи исследуемых факторов;
2. Записать основные уравнения метода наименьших квадратов, произвести необходимые преобразования, составить таблицу для промежуточных расчетов и определить параметры линейного уравнения регрессии;
3. Осуществить проверку правильности проведенных вычислений с помощью стандартных процедур и функций электронных таблиц Excel.
4. Провести анализ результатов, сформулировать выводы и рекомендации.
Содержание практического занятия № 2.2 «Оценка тесноты взаимосвязи исследуемых факторов»:
1. Расчет значения линейного коэффициента корреляции;
2. Построение таблицы дисперсионного анализа;
3. Оценка коэффициента детерминации;
4. Осуществить проверку правильности проведенных вычислений с помощью стандартных процедур и функций электронных таблиц Excel.
5. Провести анализ результатов, сформулировать выводы и рекомендации.
Содержание практического занятия № 2.3 «Оценка адекватности линейного уравнения регрессии»:
1. Оценка адекватности уравнения по значениям коэффициента аппроксимации;
2. Оценка адекватности уравнения по значениям коэффициента детерминации;
3. Оценка адекватности уравнения по критерию Фишера;
4. Провести общую оценку адекватности выбранного уравнения регрессии;
5. Осуществить проверку правильности проведенных вычислений с помощью стандартных процедур и функций электронных таблиц Excel.
6. Провести анализ результатов, сформулировать выводы и рекомендации.
Содержание практического занятия № 2.4 «Оценка значимости параметров линейного уравнения регрессии»:
1. Оценка адекватности уравнения по значениям коэффициента аппроксимации;
2. Оценка адекватности уравнения по значениям коэффициента детерминации;
3. Оценка адекватности уравнения по критерию Фишера;
4. Провести общую оценку адекватности параметров уравнения регрессии;
5. Осуществить проверку правильности проведенных вычислений с помощью стандартных процедур и функций электронных таблиц Excel.
6. Провести анализ результатов, сформулировать выводы и рекомендации.
Содержание практического занятия № 2.5 «Применения пакетов прикладных программ в эконометрических исследованиях»:
1. Использование стандартных процедур мастера функций электронных таблиц Excel (из разделов «Математические» и «Статистические»);
2. Подготовка данных и особенности применения функции «ЛИНЕЙН»;
3. Подготовка данных и особенности применения функции «ПРЕДСКАЗ».
4. Анализ результатов, выводы и рекомендации.
Содержание практического занятия № 2.6 «Применения пакетов прикладных программ в эконометрических исследованиях»:
1. Использование стандартных процедур пакета анализа данных электронных таблиц Excel;
2. Подготовка данных и особенности применения процедуры «РЕГРЕССИЯ»;
3. Интерпретация и обобщение данных таблицы регрессионного анализа;
4. Интерпретация и обобщение данных таблицы дисперсионного анализа;
5. Интерпретация и обобщение данных таблицы оценки значимости параметров уравнения регрессии;
6. Анализ результатов, выводы и рекомендации.
При выполнении лабораторной работы по данным одного из вариантов необходимо выполнить следующие частные задания:
1. Осуществить выбор формы уравнения взаимосвязи исследуемых факторов;
2. Определить параметры уравнения регрессии;
3. Провести оценку тесноты взаимосвязи исследуемых факторов;
4. Провести оценку адекватности выбранного уравнения регрессии;
5. Провести оценку статистической значимости параметров уравнения регрессии.
6. Осуществить проверку правильности проведенных вычислений с помощью стандартных процедур и функций электронных таблиц Excel.
7. Провести анализ результатов, сформулировать выводы и рекомендации.
Задания для практических и лабораторных работ по теме «Парная линейная регрессия и корреляция в эконометрических исследованиях».