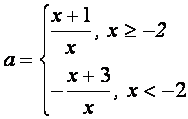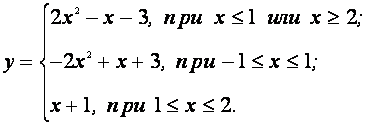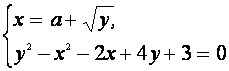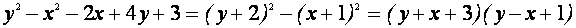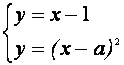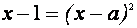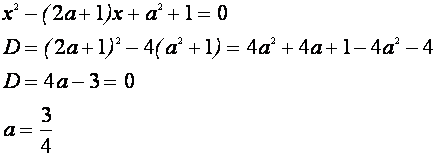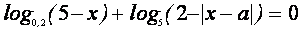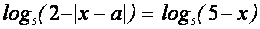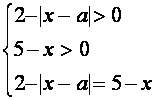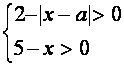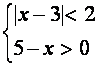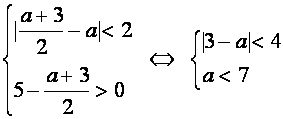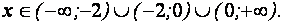Как решать систему неравенств с параметром

Содержание:

1. Основные определения

Любая система значений переменных

Решить уравнение с параметрами – значит указать, при каких значениях параметров существуют решения и каковы они.

Два уравнения, содержащие одни и те же параметры, называются равносильными, если:

а) они имеют смысл при одних и тех же значениях параметров;

б) каждое решение первого уравнения является решением второго и наоборот.

2. Алгоритм решения.

3. Примеры

I. Решить уравнение

(1)

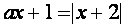
Поскольку х=0 не является корнем уравнения, то можно разрешить уравнение относительно а :

или

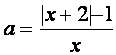
График функции – две “склеенных” гиперболы. Количество решений исходного уравнения определяется количеством точек пересечения построенной линии и прямой у=а.

II. Найти все значения параметра а, при которых уравнение 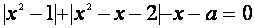имеет три различных корня.

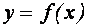
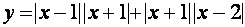
В системе координат хОу построим график функции ). Для этого можно представить её в виде и, рассмотрев четыре возникающих случая, запишем эту функцию в виде

III. Найти все значения параметра а, при каждом из которых система уравнений

Выделим в левой части второго уравнения полные квадраты и разложим её на множители

и

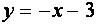
Выясним, при каких значениях параметра а кривая из семейства “полупарабол” имеет хотя бы одну общую точку с одной из полученных прямых.

Если вершины полупарабол находятся правее точки А, но левее точки В (точка В соответствует вершине той “полупараболы”, которая касается

Случай касания “полупараболы” с прямой 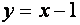определим из условия существования единственного решения системы

В этом случае уравнение

имеет один корень, откуда находим :

Ответ: а ∈ (- ∞ ;-3] ∪ ( ;+ ∞ ).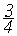

IV. Решить уравнение

Это уравнение равносильно системе

Уравнение 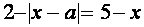перепишем в виде

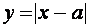
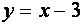
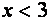
Последнее уравнение проще всего решить, используя геометрические соображения. Построим графики функций и Из графика следует, что при графики не пересекаются и, следовательно, уравнение не имеет решений.

Исследуем теперь, при каких значениях а найденные решения уравнения (*) будут удовлетворять условиям

если а ∈ (- ∞ ;3), то решений нет;

если a ∈ (3;7), то ;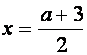

если a ∈ [7; + ∞ ), то решений нет.

V. Решить уравнение

1. При любом а :

4. По графику определяем, при каких значениях а уравнение (5) имеет решение и при каких – не имеет решения.

Источник

Факультативный курс «Линейные уравнения и неравенства с параметрами»

Окончание. Начало в № 1, 2

Рассмотрение данной темы следует начинать с краткого повторения решения линейных неравенств с одной переменной.

Упражнение 1. Решите линейное неравенство:

а) 2x > 22; б) –5x ≥ 30;
в) –0,1x ≤ 4; г) 0∙x 0; е) 0∙x ≤ 0;
ж) 0∙x ≥ –3; з) 2x – 4 > 5 – x;
и) к)
л) м) 3 – 2x 2 – 3 ≥ 9x(x + 2) – a
является решением неравенства
3x + a ≤ 2x + 1?
Решение. Решим первое неравенство:
9x 2 + 6x + 1 – 3 ≥ 9x 2 + 18x – a, 12x ≤ a – 2,
Решим второе неравенство: x ≤ 1 – a. Чтобы каждое решение первого неравенства являлось решением второго, необходимо, чтобы

Отсюда: a – 2 ≤ 12 – 12a,
Ответ: при

Упражнение 4. При каких значениях параметра a хотя бы одно решение неравенства

будет являться решением неравенства 3 – 0,5x > a?
Решение. Решив первое неравенство относительно x, получим: 8x – 8a – 12a – 12x ≤ 96,
x ≥ –5a – 24. Решив второе неравенство относительно x, получим: x –5a – 24. Откуда a > –10.
Ответ: при a > –10.

Далее разберем алгоритм решения линейных неравенств с параметрами:
1) решение линейных неравенств с одной переменной и положительным коэффициентом при этой переменной;
2) решение линейных неравенств с одной переменной и отрицательным коэффициентом при этой переменной;
3) решение неравенств с коэффициентом, равным нулю. Данный момент требует особенно пристального рассмотрения. Результат разбора полезно записать в виде таблицы.

Алгоритм решения линейных неравенств с одной переменной

Упражнение 5. Решите неравенство
(a – 1)x ≤ a 2 – 1
относительно переменной x.

Решение. Рассмотрим три случая.
1. a – 1 = 0. Тогда неравенство примет вид 0∙x ≤ 0, и его решением является любое значение переменной x.
2. a – 1 > 0. Тогда (a – 1)x ≤ a 2 – 1 ⇔ x ≤ a + 1.
3. a – 1 2 – 1 ⇔ x ≥ a + 1.

Ответ: при a = 1 x ∈ R;
при a > 1 x ≤ a + 1;
при a 2 x ≤ a 2 – 1
относительно переменной x.

Задание на дом
1. Решите неравенство (a – 2)x > a 2 – 4 относительно переменной x.
2. При каких значениях параметра a каждое решение неравенства 0,3x – 6 –2,8. Целые решения данного неравенства: –2; –1; 0; 1; 2. Решив второе неравенство, получим x 2, то есть a > 4. С другой стороны, a не может быть больше 6 (полезно оговорить случай, когда 0,5a = 3), так как тогда система будет иметь более пяти целых решений. Значит, 0,5a ≤ 3, то есть a ≤ 6.

Ответ: при 4 1 – a. Чтобы система не имела решений, необходимо, чтобы (случай обсудить отдельно). Из последнего неравенства следует: a ≤ –0,2.

Ответ: при a ≤ –0,2 система не имеет решений.

Упражнение 5. При каких значениях параметра a решением системы уравнений является пара положительных значений x и y?

Решение. Решая систему способом сложения, получим:

откуда

так как x > 0 и y > 0, то получим систему неравенств

Ответ: при a > 3 решением системы является пара положительных чисел.

Упражнение 6. При каких значениях параметра b корень уравнения 6 – 3b + 4bx = 4b + 12x меньше 1?

Решение. 6 – 3b + 4bx = 4b + 12x,
(4b – 12)x = 7b – 6.
Если b = 3, то уравнение примет вид 0∙x = 15 и не будет иметь корней.
Если b ≠ 3, то
По условию Тогда
Дробь отрицательна, если числитель и знаменатель имеют разные знаки.
Поэтому
Решив обе системы, получим: –2 2.
Если a – 1 = 0, то решения первого неравенства — x ∈ R, а решения системы — x > 2.
Если a – 1 > 0, то Здесь возможны три случая: или Рассмотрим эти случаи.
1. Пусть тогда откуда
Имеем: 1 0. Решением первой системы является неравенство a > 1,5. В этом случае система также не имеет решений.

Ответ: при a ≤ 1 x > 2;
при 1 2 + y 2 2 – 4y 2 ≤ 0.

Решение. а) График уравнения y = 2| x | – 2 разбивает плоскость на две области. Возьмем «контрольную» точку, чтобы определить, в какой из областей выполняется неравенство. Например, при подстановке координат точки A(0; 0) в неравенство получаем: 0 > 2| 0 | – 2, что верно. Значит, точка A лежит в нужной нам области.

б) Графиком уравнения являются пересекающиеся прямые x = 1 и y = –2. Используя контрольные точки, проверим, какие из областей изображают решение неравенства.

A(0; 0): (0 – 1)(0 + 2) ≥ 0 — неверно;
B(2; 2): (2 – 1)(2 + 2) ≥ 0 — верно;
C(3; – 3): (3 –1)(–3 + 2) ≥ 0 — неверно;
E(–3; –3): (–3 – 1)(–3 + 2) ≥ 0 — верно.
Простейшей линией на плоскости является прямая, разбивающая плоскость на две полуплоскости. Ордината любой точки верхней полуплоскости больше ординаты соответствующей ей точки прямой y = kx + b. В этой полуплоскости выполняется неравенство y > kx + b. В полуплоскости, расположенной ниже прямой y = kx + b, выполняется неравенство y 2 + 1)x.
2. Найдите целочисленные решения системы неравенств

3. Решите неравенство x(x – a) 2 0 x ∈ (0; a).

Ответ: при a 0 x ∈ (0; a).
Далее учащиеся самостоятельно решают упражнение 4.

Упражнение 4. Решите неравенство:
а) (x – 2a)(x – a) 2 – x 2 ≥ (x + a)(4 – a);
в)

Ответ: при a 0 x ∈ (a; 2a).
б) Преобразуем данное неравенство
(a – x)(x + a) ≥ (x + a) (4 – a),
(a – x)(x + a) – (x + a)(4 – a) ≥ 0,
(x + a)(2a – x – 4) ≥ 0.
Изобразим на координатной плоскости множество точек, соответствующих данному неравенству.

Чтобы определить координаты точки пересечения прямых, решим уравнение –x = 0,5x + 2, откуда
Тогда
Ответ:

в) Дробь если числитель и знаменатель имеют разные знаки. Поэтому

Изобразим множество точек, соответствующих неравенству

Решение. Построим график уравнения (x – a 2 )(x – | a |) = 0 в координатной плоскости Oxa, где горизонтальная ось — ось a, вертикальная — ось x, прямая a = α в этом случае будет перемещаться слева направо.

Из чертежа видно, что уравнение имеет два корня: x = a 2 и x = | a | при a 1, и один корень x = 1 при a = ±1 или x = 0 при a = 0.

Упражнение 7. Исследуйте количество решений системы уравнений

в зависимости от значений параметра m.

Решение. Решим уравнение

Тогда
(m – 4)(m + 1) = –2(m + 2), m 2 – 3m – 4 = –2m – 4, m 2 – m = 0, m = 0 или m = 1.
Рассмотрим пропорцию

При m = 0 получаем: — верно.
Значит, при m = 0 система имеет бесконечно много решений.
Если m = 1, то — неверно,
значит, при m = 1 система не имеет решений.

Ответ: при m = 0 — бесконечно много решений;
при m = 1 нет решений;
при m ≠ 0 и m ≠ 1 — единственное решение.

Упражнение 8. При каких значениях параметра a неравенство справедливо для всех x из промежутка [1; 2]?
Решение. Значение дроби отрицательно, если числитель и знаменатель имеют разные знаки. Тогда

Отсюда

Первая система имеет решения, если 2a + 1 > a, то есть при a > –1. Промежуток [1; 2] не входит во множество решений системы, если

Решением данной системы является промежуток (0,5; 1).
Вторая система имеет решения, если 2a + 1 2 (x – 2a) 2 (x – 2a) ≤ 0;
в) | x |(x – a) > 0;
г) | x + a |(x – 2) ≥ 0.

Решение. а) Так как (x – a) 2 ≥ 0 при любых значениях переменной, то неравенство
(x – a) 2 (x – 2a) 2 ≠ 0;
то есть при x a, то есть a > 0, то решение неравенства x ∈ (–∞; a) ∪(a; 2a).
Если a ≤ 0, то x ∈ (–∞; 2a).

б) Так как (x – a) 2 ≥ 0 при любых значениях переменной, то неравенство (x – a) 2 (x – 2a) ≤ 0 выполняется, если x – 2a ≤ 0 или (x – a) 2 = 0; то есть при x ≤ 2a или x = a. Если 2a ≥ a, то есть a ≥ 0,
то решение неравенства x ∈ (–∞; 2a], если a 0, если x > a, x ≠ 0. Если a ≥ 0, то x ∈ (a; +∞), если a –2, то x ∈ [2; +∞) ∪ <–a>, если
a ≤ –2, то x ∈ [2; +∞).

Упражнение 10. Решите систему неравенств

двумя способами (аналитическим и графическим с использованием системы координат Oxa).

Решение. Способ I (аналитический).

Чтобы система имела решение, необходимо, чтобы

откуда a ≥ 1. Если a > 1, то

если a = 1, то x = 1. При a 1
при a = 1 x = 1; при a 2 общих точек нет.

Источник

Квадратные уравнения и квадратичные неравенства с параметрами

Дорогой друг! Если ты никогда не решал задач с параметрами – прочитай статьи «Что такое параметр» и «Графический способ решения задач с параметрами». Квадратные уравнения, а тем более неравенства с параметрами только на первый взгляд кажутся простыми. Чтобы уверенно решать их, надо знать определенные приемы. О некоторых мы расскажем.

Разберем сначала подготовительные задачи. А в конце – реальную задачу ЕГЭ.

1. Найдите все значения a, при которых уравнение не имеет действительных корней.

Всегда ли это уравнение является квадратным относительно переменной х? – Нет, не всегда. В случае, когда коэффициент при равен нулю, оно станет линейным.

Рассмотрим два случая – когда это уравнение квадратное и когда оно линейное.

Тогда уравнение примет вид 2 = 0. Такое уравнение не имеет действительных корней, что удовлетворяет условию задачи.

Уравнение будет квадратным. Квадратное уравнение не имеет действительных корней тогда и только тогда, когда его дискриминант отрицательный.

Если и – корни квадратного уравнения
, то по теореме Виета:

Решим первое неравенство системы

Возведем второе уравнение системы в квадрат:

Значит, сумму квадратов корней уравнения можно выразить через параметр

У него единственный корень, причем положительный. Это удовлетворяет условию задачи.

Покажем один из приемов решения квадратичных уравнений и неравенств с параметрами. Он основан на следующих простых утверждениях:

— Оба корня квадратного уравнения и положительны тогда и только тогда, когда их сумма положительна и произведение положительно.

Очевидно, что сумма и произведение двух положительных чисел также положительны. И наоборот – если сумма и произведение двух чисел положительны, то и сами числа положительны.

— Оба корня квадратного уравнения и отрицательны тогда и только тогда, когда их сумма отрицательна, а произведение положительно.

Корни квадратного уравнения и имеют разные знаки тогда и только тогда, когда их произведение отрицательно.

Сумма и произведение корней входят в формулировку теоремы Виета, которой мы и воспользуемся. Получим

С учетом пункта 1 получим ответ

4. При каких значениях параметра a уравнение

имеет единственное решение?

Для того, чтобы исходное уравнение имело единственное решение, нужно, чтобы уравнение относительно t имело ровно один положительный корень.

1) В случае уравнение будет линейным

Значит, подходит. В этом случае уравнение имеет единственный положительный корень.

Дискриминант является полным квадратом и поэтому всегда неотрицателен. Уравнение имеет либо один, либо два корня. В этом случае несложно найти корни в явном виде.

Один корень получился не зависящим от параметра, причем положительным. Это упрощает задачу.

Для того, чтобы уравнение имело единственный положительный корень, нужно, чтобы либо второй был отрицательным, либо равным нулю, либо чтобы корни совпадали. Рассмотрим все случаи.

Объединив все случаи, получим ответ.

И наконец – реальная задача ЕГЭ.

5. При каких значениях a система имеет единственное решение?

Решением квадратного неравенства может быть:

В каких случаях система двух квадратных неравенств имеет единственное решение:

1) единственная общая точка двух лучей-решений ( или интервалов-решений)

2) одно из неравенств имеет решение – точку, которая является решением второго неравенства

Рассмотрим первый случай.

Если является решением 1 и 2 уравнений, то является решением уравнения (вытекает из второго первое) ⇒ или

Второй корень первого уравнения:

Второй корень второго первого:

– бесконечно много решений, не подходит.

Рассмотрим второй случай.

– решением является точка, если – является решением второго неравенства.

– решением является точка, если – не является решением первого неравенства.

Источник

Задача 18: уравнения и неравенства с параметром

Существует ровно три генеральных метода решения задач 18:

Конечно, одну и ту же задачу зачастую можно решить разными способами. Но далеко не все они оптимальны: выбрав неправильный «путь», можно увязнуть в вычислениях, так и не дойдя до ответа.

Поэтому в данном разделе я рассмотрю все способы, а ваша задача — практиковаться и учиться правильно выбирать.:)

Глава 1. Графический подход § 1. Вебинар по задачам 18: модуль и окружности § 2. Как решать задачу 18: графический подход § 3. Задача 18: две окружности и модуль § 4. Задача 18: пересечение графиков окружности и модуля § 5. Новая задача 18 из пробного ЕГЭ — наглядный пример того, как эффективно работает графическое решение задач с параметром. Глава 2. Аналитический подход § 1. Задачи 18: Аналитическое решение § 2. Окружность и модуль: задачи 18 с двумя параметрами § 3. Аналитическое решение задачи 18 с перебором различных вариантов Глава 3. Нестандартные приемы § 1. Задача 18: метод симметричных корней § 2. Как увидеть симметрию корней в задаче 18? § 3. Метод мажорант в задаче 18 § 4. Графическое решение сложных задач 18 с модулем § 5. Задание 18: Симметрия корней в системе уравнений § 6. Анализ знаков квадратного трёхчлена в сложных задачах 18 § 7. Применение производной для отыскания точек пересечения графиков § 8. Продвинутый метод симметричных корней § 9. Новая задача 18 с графическим решением

Источник