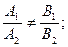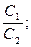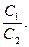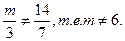Как решать слау с параметром

07.07.202214.07.2022 admin 0 Comments

Системы уравнений с двумя переменными и параметрами

п.1. Решение системы линейных уравнений с параметром

Ответ: при всех действительных a, кроме a ≠ ± 1.

п.2. Решение системы нелинейных уравнений с параметром

При решении системы нелинейных уравнений с параметром чаще всего используем графический метод (см. §15 данного справочника).

Например:
При каком значении a система уравнений имеет одно решение: \( \left\< \begin < l >\mathrm & \\ \mathrm & \end\right. \).
\( \mathrm \) – уравнение окружности с центром в начале координат, и переменным радиусом a.
\( \mathrm \) – уравнение прямой.
Система имеет одно решение, если прямая является касательной к окружности:

п.3. Примеры

Пример 2. Найти все значения параметра a, при каждом из которых система
\( \left\< \begin < l >\mathrm <|x|+|y|=4>& \\ \mathrm <(x-3)^2+(y-3)^2=(a+1)^2>& \end\right. \) имеет единственное решение.
Первое уравнение – квадрат с вершинами (±4; 0),(0; ±4); второе уравнение – окружность переменного радиуса с центром в точке (3; 3).

Единственное решение соответствует радиусу \( \mathrm>. \)
При увеличении радиуса будет 2, 3 или 4 точки пересечения. При дальнейшем увеличении окружность становится слишком большой, пересечений с квадратом нет.
Получаем:\( \mathrm<|a+1|=\sqrt<2>\Rightarrow a+1=\pm\sqrt<2>\Rightarrow a_<1,2>=-1\pm\sqrt<2>>. \)

При (a – 1) 2 2 = 4 одно решение.
При (a – 1) 2 > 4 два решения.
Получаем:\( \mathrm <(a-1)^2=4\Rightarrow a-1=\pm 2\Rightarrow>\left[\begin < l >\mathrm & \\ \mathrm & \end\right. \)

Источник

Системы линейных уравнений с параметрами

(1)

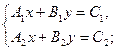
а х, у – неизвестные, называется системой двух линейных алгебраических уравнений с двумя неизвестными в параметрах.

Если из какого-нибудь уравнения системы можно найти одну из неизвестных х или у через другую, то, подставив найденную неизвестную в другое уравнение, получим линейное уравнение с параметрами относительно одной неизвестной. Тем самым, исследование системы сведётся к исследованию линейного уравнения.

Каждое из уравнений системы двух уравнений с двумя неизвестными представляют собой прямые.

На плоскости возможны три случая взаимного расположения двух прямых. Эти прямые могут:

а) пресекаться, в этом случае система (1) имеет единственное решение; коэффициенты системы удовлетворяют условию

б) совпадать, в этом случае система (1) имеет бесконечно много решений; коэффициенты системы удовлетворяют условию

= =

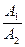
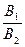
в) параллельны, в этом случае система (1) не имеет решений;

коэффициенты системы удовлетворяют условию

= ≠

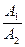
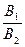
Пример 1. Определить, при каких значения m система

имеет единственное решение.

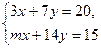
Решение: Данная система имеет единственное решение, если

Пример 2. Определить, при каком значении m система 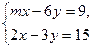не имеет решений.

Решение: Так как 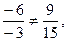то данная система не имеет реше-

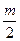
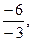
ний, если = т. е. m=4.

Пример 3. Определить, при каком значении m система 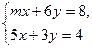имеет бесконечное множество решений.

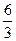
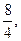
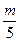
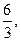
Решение: Так как = то данная система имеет бесконечное множество решений, если = т. е. при m = 10.

Источник

Урок по теме «Решение систем линейных уравнений, содержащих параметры»

Разделы: Математика

Если в задаче меньше трех переменных, это не задача; если больше восьми – она неразрешима. Энон.

Задачи с параметрами встречаются во всех вариантах ЕГЭ, поскольку при их решении наиболее ярко выявляется, насколько глубоки и неформальны знания выпускника. Трудности, возникающие у учащихся при выполнении подобных заданий, вызваны не только относительной их сложностью, но и тем, что в учебных пособиях им уделяется недостаточно внимания. В вариантах КИМов по математике встречается два типа заданий с параметрами. Первый: «для каждого значения параметра решить уравнение, неравенство или систему». Второй: «найти все значения параметра, при каждом из которых решения неравенства, уравнения или системы удовлетворяют заданным условиям». Соответственно и ответы в задачах этих двух типов различаются по существу. В первом случае в ответе перечисляются все возможные значения параметра и для каждого из этих значений записываются решения уравнения. Во втором – перечисляются все значения параметра, при которых выполнены условия задачи. Запись ответа является существенным этапом решения, очень важно не забыть отразить все этапы решения в ответе. На это необходимо обращать внимание учащихся.
В приложении к уроку приведен дополнительный материал по теме «Решение систем линейных уравнений с параметрами», который поможет при подготовке учащихся к итоговой аттестации.

Урок рассчитан на два учебных часа.

Ход урока

Сообщение темы, целей и задач урока.

Проверка домашней работы. В качестве домашнего задания учащимся было предложено решить каждую из трех систем линейных уравнений

а) б) в)

графически и аналитически; сделать вывод о количестве полученных решений для каждого случая

Ответы:

Заслушиваются и анализируются выводы, сделанные учащимися. Результаты работы под руководством учителя в краткой форме оформляются в тетрадях.

В общем виде систему двух линейных уравнений с двумя неизвестными можно представить в виде: .

Решить данную систему уравнений графически – значит найти координаты точек пересечения графиков данных уравнений или доказать, что таковых нет. Графиком каждого уравнения этой системы на плоскости является некоторая прямая.

Возможны три случая взаимного расположения двух прямых на плоскости:

К каждому случаю полезно выполнить рисунок.

Сегодня на уроке мы научимся решать системы линейных уравнений, содержащие параметры. Параметром будем называть независимую переменную, значение которой в задаче считается заданным фиксированным или произвольным действительным числом, или числом, принадлежащим заранее оговоренному множеству. Решить систему уравнений с параметром – значит установить соответствие, позволяющее для любого значения параметра найти соответствующее множество решений системы.

Решение задачи с параметром зависит от вопроса, поставленного в ней. Если нужно просто решить систему уравнений при различных значениях параметра или исследовать ее, то необходимо дать обоснованный ответ для любого значения параметра или для значения параметра, принадлежащего заранее оговоренному в задаче множеству. Если же необходимо найти значения параметра, удовлетворяющие определенным условиям, то полного исследования не требуется, и решение системы ограничивается нахождением именно этих конкретных значений параметра.

Пример 1. Для каждого значения параметра решим систему уравнений

В этом случае имеем

Система несовместна, т.е. решений не имеет.

Очевидно, что в этом случае система имеет бесконечно много решений вида x = t; где t-любое действительное число.

Пример 2. При каких значениях параметра a система уравнений

Пример 3. Найдем сумму параметров a и b, при которых система

имеет бесчисленное множество решений.

Решение. Система имеет бесчисленное множество решений, если

То есть если a = 12, b = 36; a + b = 12 + 36 =48.

а) не имеет решений; б) имеет бесконечно много решений.

Класс разбивается на группы по 4-5 человек. В каждую группу входят учащиеся с разным уровнем математической подготовки. Каждая группа получает карточку с заданием. Можно предложить всем группам решить одну систему уравнений, а решение оформить. Группа, первой верно выполнившая задание, представляет свое решение; остальные сдают решение учителю.

Карточка. Решите систему линейных уравнений

при всех значениях параметра а.

Если класс сильный, группам могут быть предложены разные системы уравнений, перечень которых находится в Приложении1. Тогда каждая группа представляет классу свое решение.

Отчет группы, первой верно выполнившей задание

Участники озвучивают и поясняют свой вариант решения и отвечают на вопросы, возникшие у представителей остальных групп.

Решение систем линейных уравнений с параметрами можно сравнить с исследованием, которое включает в себя три основных условия. Учитель предлагает учащимся их сформулировать.

При решении следует помнить:

Учитель оценивает работу на уроке класса в целом и выставляет отметки за урок отдельным учащимся. После проверки самостоятельной работы оценку за урок получит каждый ученик.

При каких значениях параметра b система уравнений

Графики функций y = 4x + b и y = kx + 6 симметричны относительно оси ординат.

Решите систему уравнений при всех значениях m и n.

Решите систему линейных уравнений при всех значениях параметра а (любую на выбор).

Источник

Решение систем линейных уравнений с параметрами

Разделы: Математика

Ход урока

2. Повторение:

I. Линейное уравнение с одной переменной:

1. Дайте определение линейного уравнения с одной переменной

[Уравнение вида ax=b, где х – переменная, а и b некоторые числа, называется линейным уравнением с одной переменной]

2. Сколько корней может иметь линейное уравнение?

[- Если а=0, b0, то уравнение не имеет решений, х

— Если а=0, b=0, то х R

— Если а0, то уравнение имеет единственное решение, х =

3. Выясните, сколько корней имеет уравнение (по вариантам)

Ответ: много корнейII ряд – II вариант

Ответ: корней нетIII ряд – III вариант

Ответ: единственный корень

II. Линейное уравнение с 2 –мя переменными и система линейных уравнений с 2- мя переменными.

1. Дайте определение линейного уравнения с двумя переменными. Приведите пример.

[Линейным уравнением с двумя переменными называются уравнения вида ах +by=с, где х и у – переменные, а, b и с – некоторые числа. Например, х-у=5]

2. Что называется решением уравнения с двумя переменными?

[Решением уравнения с двумя переменными называются пара значений переменных, обращающие это уравнение в верное равенство.]

3. Является ли пара значений переменных х = 7, у = 3 решением уравнения 2х + у = 17?

4. Что называется графиком уравнения с двумя переменными?

[Графиком уравнения с двумя переменными называется множество всех точек координатной плоскости, координаты которых является решениями этого уравнения.]

5. Выясните, что представляет собой график уравнения:

[Выразим переменную у через х: у=-1,5х+3

Формулой у=-1,5х+3 является линейная функция, графиком которой служит прямая. Так как, уравнения 3х+2у=6 и у=-1,5х+3 равносильны, то эта прямая является и графиком уравнения 3х+2у=6]

6. Что является графиком уравнения ах+bу=с с переменными х и у, где а0 или b0?

[Графиком линейного уравнения с двумя переменными, в котором хотя бы один из коэффициентов при переменных не равен нулю, является прямая.]

7. Что называется решением системы уравнений с двумя переменными?

[Решением системы уравнений с двумя переменными называется пара значений переменных, обращающая каждое уравнение системы в верное равенство]

8. Что значит решить систему уравнений?

[Решить систему уравнений – значит найти все ее решения или доказать, что решений нет.]

9. Выясните, всегда ли имеет такая система решения и если имеет, то сколько (графическим способом).

10. Сколько решений может иметь система двух линейных уравнений с двумя переменными?

[Единственное решение, если прямые пересекаются; не имеет решений, если прямые параллельны; бесконечно много, если прямые совпадают]

11. Каким уравнением обычно задается прямая?

12. Установите связь между угловыми коэффициентами и свободными членами:

k₁ = k₂, b₁ = b_2, много решений.

На доске таблица, которую постепенно заполняет учитель вместе с учениками.

III. Объяснение новой темы.

где A_1, A_2, B₁,B_2, C₁ C_{2 –} выражения_, зависящие от параметров, а х и у – неизвестные, называется системой двух линейных алгебраических уравнений с двумя неизвестными в параметрах.

Возможны следующие случаи:

1) Если , то система имеет единственное решение

2) Если , то система не имеет решений

3) Если , то система имеет бесконечно много решений.

IV. Закрепление

Пример 1.

а) имеет бесконечное множество решений;

б) имеет единственное решение

а) , а=4

б) , а?4

а) если а=4, то система имеет бесконечное множество решений;

б) если а4, то решение единственное.

Пример 2.

Решение: а) , т.е. при m1 система имеет единственное решение.

б) , т.е. при m=1 (2=m+1) и n1 исходная система решений не имеет

в) , при m=1 и n=1 система имеет бесконечно много решений.

Ответ: а) если m=1 и n1, то решений нет

y= x=

Пример 3.

Решение: Из II уравнения найдем х=1-ау и подставим в I уравнение

1) а=0. Тогда уравнение имеет вид 0*у=3 [у ]

Следовательно, при а=0 система не имеет решений

Следовательно, у . При этом х=1-ау=1+3у

3) а0 и а-3. Тогда у=-, х=1-а(-=1+1=2

1) если а=0, то (х; у)

2) если а=-3, то х=1+3у, у

3) если а0 и а?-3, то х=2, у=-

Рассмотрим II способ решения системы (1).

Решим систему (1) методом алгебраического сложения: вначале умножим первое уравнение системы на В_2, второе на – В₁ и сложим почленно эти уравнения, исключив, таким образом, переменную у:

Т.к. А₁В₂-А₂В₁0, то х =

т.к. А₂В₁-А₁В₂ 0 у =

Для удобства решения системы (1) введем обозначения:

_— главный определитель

Теперь решение системы (1) можно записать с помощью определителей:

х= ; у=

Приведенные формулы называют формулами Крамера.

— Если , то система (1) имеет единственное решение: х=; у=

— Если , или , , то система (1) не имеет решений

— Если , , , , то система (1) имеет бесконечное множество решений.

В этом случае систему надо исследовать дополнительно. При этом, как правило, она сводится к одному линейному уравнению. В случае часто бывает удобно исследовать систему следующим образом: решая уравнение , найдем конкретные значения параметров или выразим один из параметров через остальные и подставим эти значения параметров в систему. Тогда получим систему с конкретными числовыми коэффициентами или с меньшим числом параметров, которую надо и исследовать.

Если коэффициенты А₁, А₂, В₁, В₂, системы зависят от нескольких параметров, то исследовать систему удобно с помощью определителей системы.

Пример 4.

Решение: Найдем определитель системы:

1) Тогда