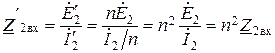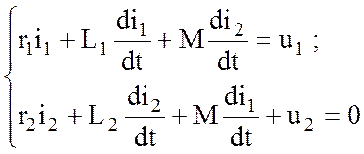Как связаны между собой реальные и приведенные параметры цепи вторичной обмотки

ЛЕКЦИЯ 15. Параметры приведенной вторичной обмотки и схема замещения трансформатора

Параметры приведенной вторичной обмотки и схема замещения трансформатора. Приведенный трансформатор

Неравенство витков первичной и вторичной обмоток усложняет расчет электрических цепей, элементами которых является трансформатор, т. к.:

-трансформаторы соединяют разные участки электрических цепей электромагнитным путем, электрически эти участки не связаны, т. к. w₁не равно w₂, то и не равны Е₁ и Е₂. Если в электрической цепи n трансформаторов, то n раз приходится изменять по значению ток и напряжение ;

Магнитная связь между обмотками усложняет анализ трансформаторов. Для его упрощения составляют эквивалентную электрическую схему, в которой магнитная связь заменяется гальванической. Получил распространение способ приведения вторичной обмотки трансформатора к первичной.

Приведенная вторичная обмотка содержит то же количество витков, что и первичная, т. е. w = w₁. Поскольку ЭДС обмоток после приведения становятся одинаковыми

, ,

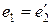
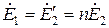
Операция приведения увеличивает ЭДС E₂ в n раз.

Для сохранения мощностей всех элементов вторичной цепи ее параметры нужно пересчитать так, чтобы ток I₂ уменьшился в n раз, т. е. = ₂/n. Это означает, что входное сопротивление вторичной цепи

должно увеличиться в n 2 раз. Тогда для получения приведенных сопротивлений сопротивления всех элементов вторичной цепи нужно увеличить в n 2 раз:

;;.

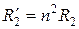
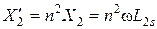
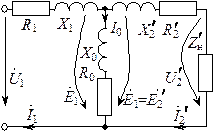
Таким образом следует, что ток ветви с элементами X₀, R₀ равен намагничивающему току İ₀ (эту ветвь называют намагничивающей). Сопротивление R₀ введено с целью учета тепловых потерь в сердечнике за счет гистерезиса и вихревых токов. Параметры X₀, R₀ определяются экспериментально, из опыта холостого хода.

Источник

Приведение параметров вторичной обмотки и схема замещения приведенного трансформатора

В общем случае параметры первичной обмотки трансформатора отличаются от параметров вторичной обмотки. Эта разница наиболее ощутима при больших коэффициентах трансформации, что затрудняет расчеты и построение векторных диаграмм, так как в этом случае векторы электрических величин первичной обмотки значительно отличаются по своей длине от одноименных векторов вторичной обмотки. Указанные затруднения устраняются приведением всех параметров трансформатора к одинаковому числу витков, обычно к числу витков первичной обмотки w₁. С этой целью все величины, характеризующие вторичную цепь трансформатора, — ЭДС, напряжение, ток и сопротивления — пересчитывают на число витков w₁ первичной обмотки.

Таким образом, вместо реального трансформатора с коэффициентом трансформации k = w₁/w₂ получают эквивалентный трансформатор с k=w₁/w’₂=1, где w’₂=w₁. Такой трансформатор называют приведенным. Однако приведение вторичных параметров трансформатора не должно отразиться на его энергетических показателях: все мощности и фазовые сдвиги во вторичной обмотке приведенного трансформатора должны остаться такими, как и в реальном трансформаторе.

Так, электромагнитная мощность вторичной обмотки реального трансформатора Е₂I₂ должна быть равна электромагнитной мощности вторичной обмотки приведенного трансформатора:

(1.27)

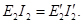
Подставив значение приведенного тока вторичной обмотки I₂= I₂(w₂/w₁,) в (1.27), получим формулу приведенной вторичной ЭДС:

(1.28)

(1.29)

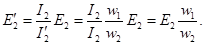
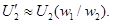
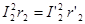
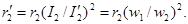
Из условия равенства потерь в активном сопротивлении вторичной обмотки имеем . Определим приведенное активное сопротивление:

(1.30)

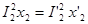
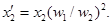
Приведенное индуктивное сопротивление рассеяния вторичной обмотки определяют из условия равенства реактивных мощностей ,откуда

(1.31)

Приведенное полное сопротивление вторичной обмотки трансформатора

(1.32)

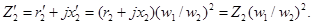
Приведенное полное сопротивление нагрузки, подключенной на выводы вторичной обмотки, определим по аналогии с (1.32):

(1.33)

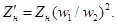
Уравнения напряжений и токов для приведенного трансформатора имеют вид

(1.34)

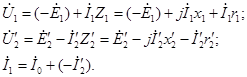
Эти уравнения устанавливают аналитическую связь между параметрами трансформатора во всем диапазоне нагрузок от режима х.х. до номинальной.

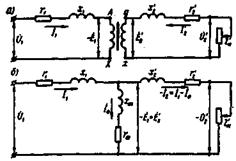
Еще одним средством, облегчающим исследование электромагнитных процессов и расчет трансформаторов, является применение электрической схемы замещения приведенного трансформатора. На рис. 1.18, а представлена эквивалентная схема приведенного трансформатора, на которой сопротивления r и х условно вынесены из соответствующих обмоток и включены последовательно им. Как было установлено ранее, в приведенном трансформаторе k = 1, а поэтому 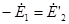. В результате точки А и а, атакже точки X и х на схеме имеют одинаковые потенциалы, что позволяет электрически соединить указанные точки, получив Т–образную схему замещения приведенного трансформатора (рис. 1.18, б). В электрической схеме замещения трансформатора магнитная связь между цепями заменена электрической.

Рис. 1.18. Эквивалентная схема (в) и схема замещения (б) приведенного

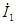
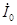
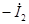
Схема замещения приведенного трансформатора удовлетворяет всем уравнениям ЭДС и токов приведенного трансформатора (1.34) и представляет собой совокупность трех ветвей: первичной — сопротивлением Z₁ = r₁ + jx₁ и током ; намагничивающей — сопротивлением Z_m=r_m+jx_m и током ; вторичной — с двумя сопротивлениями: сопротивлением собственно вторичной ветви Z’₂ = r’₂ + jx’₂ и сопротивлением нагрузки Z’_H = r_н‘ ± jx’_H и током . Изменением сопротивления нагрузки Z’_H на схеме замещения могут быть воспроизведены все режимы работы трансформатора.

Параметры ветви намагничивания Z_m = r_m + jx_m определяются током х.х. Наличие в этой ветви активной составляющей r_m обусловлено магнитными потерями в трансформаторе (см. § 1.14).

Все параметры схемы замещения, за исключением Z’_H, являются постоянными для данного трансформатора и могут быть определены из опыта х.х. и опыта к.з. (см. §1.11).

Источник

где – эквивалентная индуктивность схемы;

– эквивалентное сопротивление схемы.

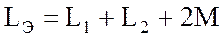
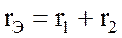
Встречное включение (см. рис.3.24,б) характеризует следующее уравнение

, (3.75)

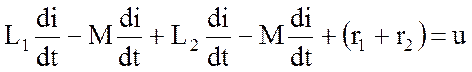
где дополнительные падения напряжения 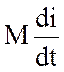, обусловленные взаимной магнитной связью катушек, вычитаются.

Поэтому после преобразований получаем:

;

, (3.76)

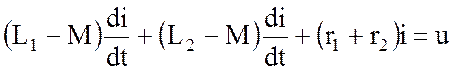
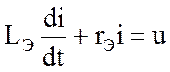
где ; .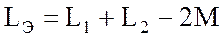

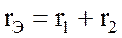
В первом случае, как следует из (3.74), взаимная индуктивность М обусловливает увеличение эквивалентной индуктивности. В данном случае эквивалентная индуктивность уменьшается, но остается величиной положительной в любых условиях.

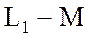
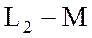
Разности и в (3.76) могут быть как положительными, так и отрицательными, но не одновременно.

Уравнения (3.73) и (3.76) можно записать в комплексной форме, например, относительно комплексных действующих значений напряжений и тока:

для согласного включения

;

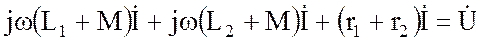
для встречного включения

. (3.77)

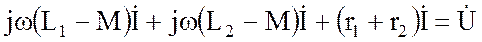
Степень магнитной связи между двумя катушками характеризует параметр

, (3.78)

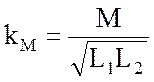
который называют коэффициентом магнитной связи. Этот коэффициент в зависимости от условий имеет значения в диапазоне от нуля до единицы. Нулевое значение k_м достигается в случаях, когда оси катушек взаимно перпендикулярны. Максимальное значение, близкое к единице, может быть получено при так называемой бифилярной намотке, когда намотка обеих катушек осуществляется соприкасающейся парой проводов.

3.10.2. Магнитно-связанные цепи без электрической связи

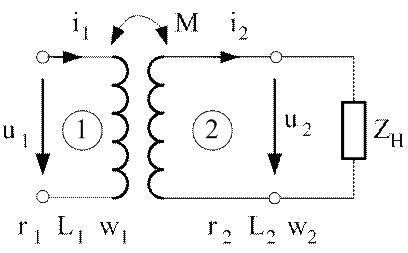
Схема простейшего двухобмоточного воздушного трансформатора изображена на рис.3.26.

Рис.3.26. Воздушный трансформатор

Все параметры первичной обмотки имеют индекс единицу, вторичной обмотки – двойку.

Электрическое соединение между первичной и вторичной обмотками отсутствует. Энергия во вторичный контур передается через изменяющееся во времени магнитное поле.

Схема рассматриваемого трансформатора двухконтурная, поэтому можно записать два уравнения по второму закону Кирхгофа:

(3.79)

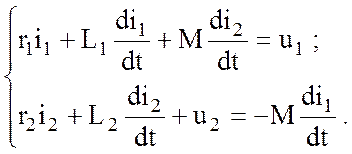
Здесь величина – 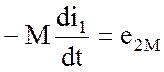представляет собой ЭДС взаимной индукции, которая током первичной обмотки i₁ наводится во вторичной обмотке. Именно эта ЭДС обусловливает ток i₂ во вторичной обмотке трансформатора и нагрузке Z_н.

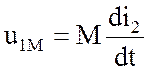
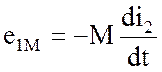
Составляющая в первом уравнении (3.79) является падением напряжения, которое компенсирует ЭДС взаимной индукции , наводимой током вторичной обмотки i₂ в первичной обмотке. Наличие ЭДС e_1M и e_2M характеризуют двухстороннюю магнитную связь в схеме воздушного трансформатора.

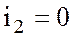
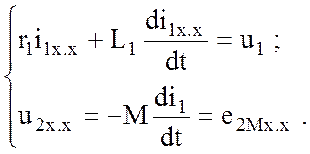
В режиме холостого хода, когда вторичный контур разомкнут, ток и система (3.79) приобретает вид

(3.80)

В этом режиме магнитная связь односторонняя, поскольку магнитный поток вторичной обмотки отсутствует.

Уравнения (3.79) в комплексной форме имеют вид:

(3.81)

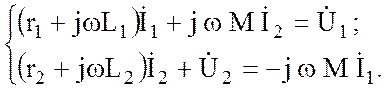
Решение этих уравнений позволяет определить токи первичной и вторичной обмоток и исследовать режимы трансформатора в полном диапазоне изменения параметров, т.е. от режима холостого хода до режима короткого замыкания (Z_н = 0).

Чтобы распечатать файл, скачайте его (в формате Word).

Источник

Большая Энциклопедия Нефти и Газа

Параметры вторичной обмотки ТТ ( гт2 и хт2) обычно указываются в технических данных на ТТ. [1]

При этом параметры вторичной обмотки должны быть надлежащим образом пересчитаны, чтобы сохранить реальные энергетические соотношения в машине. [3]

При определении параметров вторичной обмотки приведенного трансформатора все параметры первичной его обмотки остаются неизменными. При замене реального трансформатора приведенным активные, реактивные и полные мощности, а также коэффициент мощности вторичной обмотки трансформатора остаются постоянными. [4]

В процессе определения параметров вторичной обмотки приведенного трансформатора все параметры первичной его обмотки остаются неизменными. При замене реального трансформатора приведенным трансформатором активные, реактивные и полные мощности, а также коэффициент мощности вторичной обмотки трансформатора должны оставаться постоянными. [5]

При этом все величины и параметры вторичной обмотки приводят к числу витков первичной обмотки таким образом, чтобы физические процессы в приведенном трансформаторе не отличались от процессов в реальном трансформаторе. [6]

Как уже указывалось ранее, все параметры вторичных обмоток приводятся к первичной. [7]

Исследование работы трансформатора при нагрузке производится на основе векторных диаграмм, построенных для приведенного трансформатора, у которого параметры вторичной обмотки приведены к напряжению U и числу витков w первичной обмотки. При замене реального трансформатора приведенным активные, реактивные и полные мощности, а также коэффициент мощности вторичной обмотки трансформатора принимаются неизменными. [11]

Однако указанное приведение параметров трансформатора не должно отразиться на его энергетических показателях: все мощности и фазовые сдвиги параметров вторичной обмотки приведенного трансформатора должны остаться такими, как и в реальном трансформаторе. [12]

Исследование работы трансформатора при нагрузке удобно производить на основе векторных диаграмм, построенных для приведенного трансформатора, у которого параметры вторичной обмотки приведены к напряжению и числу витков первичной обмотки. [13]

Исследование работы трансформатора при нагрузке удобно производить на основе векторных диаграмм, построенных для приведенного трансформатора, заменяющего реальный трансформатор, у которого параметры вторичной обмотки приведены к напряжению и числу витков первичной обмотки. [14]

Исследование работы трансформатора при нагрузке удобно проводить на основе векторных диаграмм, построенных для приведенного трансформатора, заменяющего реальный трансформатор, у которого параметры вторичной обмотки приведены к напряжению и числу витков первичной обмотки. [15]

Источник

Электрическая схема замещения трансформатора

Параметры первичной и вторичной обмоток трансформатора отличаются, что наиболее ощутимо при больших коэффициентах трансформации и затрудняет построение векторных диаграмм.

Названное затруднение устраняется процедурой, называемой приведением параметров вторичной обмотки и нагрузки к первичной, они пересчитываются на число витков, равное числу витков первичной обмотки w1. В результате вместо реального трансформатора с коэффициентом трансформации

получают эквивалентный трансформатор с

Такой трансформатор называют приведенным.

Приведение вторичных параметров не должно отразиться на энергетических показателях трансформатора: все мощности и фазовые сдвиги во вторичной обмотке приведенного трансформатора должны остаться такими, как в реальном трансформаторе. В результате число витков вторичной обмотки изменится в раз и как следствие этого

Из условия равенства электромагнитных мощностей вторичных обмоток реального и приведенного трансформаторов получаем выражение для приведенного тока вторичной обмотки

Из условия равенства потерь в активном сопротивлении вторичных обмоток реального и приведенного трансформаторов получаем выражение для приведенного активного сопротивления вторичной обмотки

Приведенное индуктивное сопротивление рассеяния вторичной обмотки определяем из условия равенства реактивных мощностей вторичных обмоток реального и приведенного трансформаторов

Приведенное полное сопротивление вторичной обмотки трансформатора

Уравнения напряжений для приведенного трансформатора

Эти уравнения устанавливают аналитическую связь между параметрами трансформатора в диапазоне нагрузок от режима холостого хода до номинальной.

Изобразим эквивалентную схему трансформатора (рис.1.5,а). На этой схеме активные и индуктивные сопротивления условно вынесены из соответствующих обмоток и включены последовательно.

Т-образная электрическая схема замещения приведенного трансформатора облегчает исследование электромагнитных процессов и расчет трансформаторов. Схема представляет собой совокупность трех ветвей. Первая: с сопротивлением

Источник