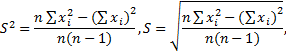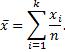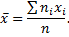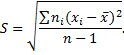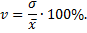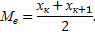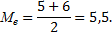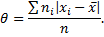Какие бывают виды оценок статистических параметров
Статистические оценки
Связанные понятия
Упоминания в литературе
Связанные понятия (продолжение)
В статистике метод оценки с помощью апостериорного максимума (MAP) тесно связан с методом максимального правдоподобия (ML), но дополнительно при оптимизации использует априорное распределение величины, которую оценивает.
Функция предельного правдоподобия (англ. Marginal Likelihood Function) или интегрированное правдоподобие (англ. integrated likelihood) — это функция правдоподобия, в которой некоторые переменные параметры исключены. В контексте байесовской статистики, функция может называться обоснованностью (англ. evidence) или обоснованностью модели (англ. model evidence).
В математике и физике, выборка по уровням это разновидность выборки методом случайных блужданий, основывающаяся на том факте что для выборки функции с заданным распределением достаточно производить равномерноую выборку из области под графиком плотности вероятности.
Модели дискретного выбора — экономические (эконометрические) модели, позволяющие описывать, объяснять и прогнозировать выбор между, двумя или более альтернативами (то есть когда множество альтернатив не более чем счетно). Модели дискретного выбора позволяют на основе некоторых характеристик (атрибутов) экономического субъекта или ситуации оценить вероятность выбора той или иной альтернативы.
Т-критерий Вилкоксона — (также используются названия Т-критерий Уилкоксона, критерий Вилкоксона, критерий знаковых рангов Уилкоксона, критерий суммы рангов Уилкоксона) непараметрический статистический тест (критерий), используемый для проверки различий между двумя выборками парных или независимых измерений по уровню какого-либо количественного признака, измеренного в непрерывной или в порядковой шкале.. Впервые предложен Фрэнком Уилкоксоном. Другие названия — W-критерий Вилкоксона, критерий знаковых.
СТАТИСТИЧЕСКИЕ ОЦЕНКИ
Изучив эту главу, студент будет знать, что выборка может рассматриваться как эмпирический аналог генеральной совокупности, что с помощью выборочных данных можно судить о свойствах генеральной совокупности и оценивать ее характеристики, основные законы распределения статистических оценок, уметь производить точечные и интервальные оценки параметров генеральной совокупности методом моментов и максимального правдоподобия, владеть способами определения точности и надежности полученных оценок.
Виды статистических оценок
О параметрах генеральной совокупности мы знаем то, что они объективно существуют, но определить их непосредственно невозможно в силу того, что генеральная совокупность или бесконечна или чрезмерно велика. Поэтому может стоять вопрос только об оценке этих характеристик.
Ранее было установлено, что для выборки, извлеченной из генеральной совокупности, при соблюдении условий репрезентативности, можно определить характеристики, которые являются аналогами характеристик генеральной совокупности.
cjp Определение 8.1. Приближенные значения параметров распределения, найденные по выборке, называются оценкой параметра.
Обозначим оцениваемый параметр случайной величины (генеральной совокупности) как 0, а его оценку, полученную с помощью выборки, 0.
Оценка 0 является случайной величиной, поскольку любая выборка является случайной. Оценки, полученные для разных выборок, будут отличаться друг от друга. Поэтому будем считать 0 функцией, зависящей от выборки: 0 = 0(Хв).
ЩР Определение 8.2. Статистическая оценка называется состоятельной, если она стремиться по вероятности к оцениваемому параметру:
Это равенство означает, что событие 0=0 становится достоверным при неограниченном возрастании объема выборки.
В качестве примера можно привести относительную частоту некоторого события А, которая является состоятельной оценкой вероятности этого события в соответствии с теоремой Пуассона (см. формулу (6.1), часть 1).
Определение 8.3. Статистическая оценка называется эффективной, если она имеет наименьшую дисперсию при одних и тех же объемах выборки.
Сначала сделаем важное утверждение: учитывая то, что все случайные величины X, извлекаются из одной и той же генеральной совокупности X, а значит, имеют одно и то же распределение что и X, можно записать:
Таким образом, выборочная средняя является статистической оценкой математического ожидания случайной величины. Эта оценка является состоятельной поскольку в соответствии со следствием из теоремы Чебышева она сходится по вероятности к математическому ожиданию (6.3).
Мы установили, что в рассматриваемом случае математическое ожидание выбранной нами оценки (случайной величины) равно самому оцениваемому параметру. Оценки, обладающие таким свойством, занимают особое место в математической статистике, они называются несмещенными.
Определение 8.4. Статистическая оценка © называется несмещенной, если ее математическое ожидание равно оцениваемому параметру 
Если это требование не выполнено, то оценка называется смещенной.
Таким образом, выборочная средняя является несмещенной оценкой математического ожидания.
Преобразуем каждое из двух полученных слагаемых:
Здесь было использовано равенство М(Х.) = М(Х 2 ), справедливое по той же причине, что и (8.1).
Рассмотрим второе слагаемое. С помощью формулы квадрата суммы п слагаемых получаем
учитывая снова равенство (8.1), а также то, что X. и X независимые случайные величины запишем
и окончательно получим:
Подставим полученные результаты в (8.3) 
После преобразования получим
Таким образом, можно сделать вывод, что выборочная дисперсия является смещенной оценкой генеральной дисперсии.
Учитывая полученный результат, поставим задачу построить такую оценку генеральной дисперсии, которая удовлетворяла бы условию несмещенности (8.2). Для этого рассмотрим случайную величину
Легко видеть, что для этой величины условие (8.2) выполняется:
Следовательно, 5 2 можно считать несмещенной оценкой генеральной дисперсии. Эта величина называется исправленной выборочной дисперсией. Значение исправленной дисперсии для конкретной выборки рассчитывается по формуле
Заметим, что различие между выборочной дисперсией и исправленной выборочной дисперсией становятся незначительными при больших объемах выборки.
При выборе оценок характеристик случайных величин важно знать их точность. В некоторых случаях требуется высокая точность, а иногда достаточно иметь грубую оценку. Например, планируя перелет с пересадкой нам важно знать как можно точнее планируемое время прилета к месту стыковки авиарейсов. В другой ситуации, например, находясь дома и ожидая курьера с заказанным нами товаром, высокая точность времени его прибытия для нас не важна. В обоих случаях случайной величиной является время прибытия, а интересующей нас характеристикой случайной величины — среднее время в пути.
Оценки бывают двух видов. В первом случае ставится задача получить конкретное числовое значение параметра. В другом случае определяется интервал, в который с заданной вероятностью попадает интересующий нас параметр.
Виды статистических оценок параметров распределения
Все статистические оценки подразделяют на точечные и интервальные.
Статистика, используемая в качестве приближенного значения неизвестного параметра генеральной совокупности, называется ее точечной оценкой. Таким образом, точечная оценка определяется одним числом.
Если рассматривают выборку малого объема, то точечная оценка
может значительно отличаться от оцениваемого параметра, т.е. приводить к грубым ошибкам. По этой причине при небольшом объеме выборки следует пользоваться интервальными оценками.
Выборочной средней 
называют среднее арифметическое значение признака выборочной совокупности. Если все значения признака 
выборки объема n различны, то находится по формуле
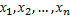
Если значения признака 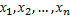имеют соответствующие частоты, то среднюю выборочную рассчитывают следующим образом
Таким образом, выборочная средняя, найденная по данным одной выборки, есть конкретное число.
Если извлекать другие выборки того же объема из одной генеральной совокупности, то выборочная средняя будет изменяться от выборки к выборке.
Вывод: выборочную среднюю можно рассматривать как случайную величину, т.е. можно говорить о распределениях (теоретическом и эмпирическом) выборочной средней и о числовых характеристиках этого распределения.
Отклонением от общей средней называют разность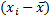 
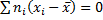
между значением признака и общей средней. Сумма произведений отклонений на соответствующие частоты равна нулю
.
Выборочной дисперсией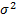 
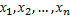
называют среднее арифметическое квадратов отклонения наблюдаемых значений признака от их среднего значения . Если значения признака имеют соответственно частоты 
и 
, то выборочная дисперсия рассчитывается по формуле
Кроме дисперсии для характеристики рассеяния значений признака выборочной совокупности вокруг своего среднего значения используют еще одну характеристику – среднее квадратическое отклонение. Выборочным средним квадратическим отклонением называют квадратный корень из выборочной дисперсии
Среднее квадратическое отклонение – это обобщающая характеристика размеров вариации признака в совокупности. Среднее квадратическое отклонение показывает, насколько в среднем отклоняются конкретные варианты от их среднего значения.
По вышеуказанным данным выборки, возможно, оценить неизвестные генеральную дисперсию и генеральное среднее квадратическое отклонение. Для этого используют несмещенную оценку генеральной совокупности – исправленную дисперсию
Для оценки среднеквадратического отклонения генеральной совокупности используют исправленное среднее квадратическое отклонение, которое не является несмещенной оценкой
Коэффициент вариации представляет собой выраженное в процентах отношение среднеквадратического отклонения к средней арифметической
Коэффициент вариации используют для сравнительной оценки вариации единиц совокупности и как характеристику однородности совокупности. Совокупность считается количественно однородной, если коэффициент вариации не превышает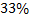 
.
Кроме перечисленных выше характеристик вариационного ряда используют и другие, такие как мода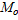 
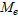
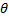
, медиана 
, среднее абсолютное отклонение 
.
Модой 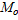называют варианту, которая имеет наибольшую частоту.
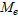
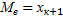
Медианой называют варианту, которая делит вариационный ряд на две части, равные по числу вариант. Если число вариант нечетно, т.е. n=2k+1, то 
; если число вариант четно, т.е. n=2k, то
Например, для ряда 2 3 5 6 7 медиана равна 5; для ряда 2 3 5 6 7 9 медиана равна
Средним абсолютным отклонением 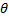называют среднее арифметическое абсолютных отклонений
Среднее абсолютное отклонение служит для характеристики рассеяния вариационного ряда.
Интервальной называют оценку, которая определяется двумя числами – концами интервала. Интервальные оценки позволяют установить точность и надежность оценок.
Дата добавления: 2015-08-11 ; просмотров: 2009 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
18.6.5. Статистические оценки параметров распределения
Несмещенной называется статистическая оценка 
, математическое ожидание которой равно оцениваемому параметру 
при любой выборке:
Смещенной называется оценка, при которой условие (18.51) не выполнено. Эффективной называется оценка, которая имеет минимальную дисперсию при заданном объеме выборки П. Состоятельной называется статистическая оценка типа (18.50), которая при П >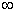 
стремится по вероятности к оцениваемому параметру.
Теперь укажем виды числовых характеристик оценок. Прежде всего, это средние. Генеральная средняя для изучаемого количественного признака Х по генеральной совокупности
И Выборочная средняя
Можно показать, что выборочная средняя (18.52) является несмещенной оценкой; это аналог математического ожидания случайной величины.
Введем в рассмотрение величины, характеризующие отклонение значений количественного признака Х от своего среднего значения. Это Генеральная дисперсия:
И выборочная дисперсия:
Можно показать, что для вычисления этих характеристик справедливы более удобные формулы, аналогичные дисперсии случайной величины; так, формула (18.53) принимает вид
Генеральное среднее квадратическое отклонение определяется как
Аналогично вводится и Выборочное среднее квадратическое отклонение
Пример 4. Выборка задана таблицей распределения
Найти выборочные характеристики: среднюю, дисперсию и среднее квадратическое отклонение.
Решение. По формуле (18.52) сначала находим 
В:
Затем по формулам (18.54) и (18.55) находим две другие искомые величины:
Статистическое оценивание
Материал из MachineLearning.
Содержание
Постановка задачи
Различают два основных типа оценок: точечные оценки и доверительные интервалы.
Точечное оценивание
К общим методам построения точечных оценок параметров относятся: метод максимального правдоподобия, метод моментов, метод квантилей.
Ниже приводятся некоторые свойства, которыми могут обладать или не обладать точечные оценки.
Состоятельность
Когда употребляют просто термин состоятельность, то обычно имеется в виду слабая состоятельность, т.е. сходимость по вероятности.
Условие состоятельности является практически обязательным для всех используемых на практике оценок. Несостоятельные оценки используются крайне редко.
Несмещенность и асимптотическая несмещенность
Оценка параметра называется несмещенной, если ее математическое ожидание равно истинному значению оцениваемого параметра:
Более слабым условием является асимптотическая несмещенность, которая означает, что математическое ожидание оценки сходится к истинному значению параметра с ростом объема выборки:
Сравнение оценок и эффективность
Для сравнения между собой различных оценок одного и того же параметра применяют следующий метод: выбирают некоторую функцию риска, которая измеряет отклонение оценки от истинного значения параметра, и лучшей считают ту, для которой эта функция принимает меньшее значение.
Чаще всего в качестве функции риска рассматривают математическое ожидание квадрата отклонения оценки от истинного значения
Существует нижняя граница на данную функцию риска, называемая неравенство Крамера-Рао.
(Несмещенные) оценки, для которых достигается эта нижняя граница (т.е. имеющие минимально возможную дисперсию), называются эффективными. Однако существование эффективной оценки есть довольно сильное требование на задачу, которое имеет место далеко не всегда.
Достаточные статистики
(Несмещенная) эффективная оценка параметра всегда является достаточной статистикой.
Доверительные интервалы
Другим типом оценок статистических параметров являются доверительные интервалы.
Доверительные интервалы используются, когда нам нужны надежные границы, в которые попадает значение оцениваемого параметра.
Часто вместе с точечной оценкой параметра строят доверительный интервал, середина которого равна этой оценке. Его ширина является наглядной характеристикой того, насколько точна может быть данная точечная оценка.
Иногда бывает наоборот: естественным образом строится некоторый доверительный интервал, а в качестве точечной оценки параметра рассматривают его середину.