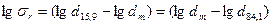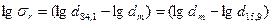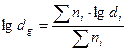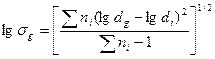Какие параметры характеризуют величину дисперсности

Коллоидная химия. Шпаргалка

Данное издание создано в помощь студентам вузов, которые хотят быстро подготовиться к экзаменам и сдать сессию без проблем. Пособие составлено с учетом Государственного образовательного стандарта.

Оглавление

Приведённый ознакомительный фрагмент книги Коллоидная химия. Шпаргалка предоставлен нашим книжным партнёром — компанией ЛитРес.

4. Дисперсность. Удельная поверхность дисперсных систем, методы ее измерения

Основная характеристика дисперсных систем — размеры частиц, или дисперсность. Дисперсные системы делят на грубодисперсные (низкодисперсные) и тонкодисперсные (высокодисперсные), или коллоидные системы (коллоиды). В грубодисперсных системах частицы имеют размер от 10 –4 см и выше, в коллоидных — от 10 –4 до 10 –5 — 10 –7 см. Дисперсность определяется по трем измерениям тела, либо характеризуется величиной, обратной минимальному размеру и названной дисперсностью, либо через удельную площадь поверхности S_уд (отношение межфазной поверхности к объему тела). Количественной характеристикой дисперсности (раздробленности) вещества является степень дисперсности (степень раздробленности D) — величина, обратная размеру дисперсных частиц а: D = 1/a, где а равно диаметру сферических или волокнистых частиц, или длине ребра кубических частиц, или толщине пленок. Все частицы дисперсной фазы имеют одинаковые размеры — монодисперсная система. Частицы дисперсной фазы неодинакового размера — полидисперсная система. Соотношение между поверхностью и объемом характеризует удельная поверхность:

Для частиц сферической формы она равна:

Для частиц кубической формы —

где r — радиус шара; d — его диаметр; l — длина ребра куба.

Дисперсность D связана с удельной поверхностью S_уд:

где V — объем дисперсной фазы, мл.

Для сферических частиц уравнение принимает вид:

Формула для расчета удельной поверхности (S_уд) системы с шарообразными частицами:

где n — число частиц, м 3 ; S₀ — поверхность каждой частицы.

Корреляционная спектроскопия рассеянного света: в определенном оптическом объеме V₀, подсчитывают число частиц n. Зная концентрацию частиц С и n, находят объем частицы : = С / (vd),

где d — плотность дисперсной фазы.

Зная объем, можно вычислить радиус частиц:

Зная радиус частиц, можно вычислить удельную поверхность S_уд.

Источник

Параметры и свойства дисперсных систем

Основные физико-химические свойства аэродисперсных систем.

Тема 3

Многофазные системы принято называть дисперсными системами, состоящими из дисперсной фазы и дисперсионной среды. Поскольку аэрозоль является дисперсной фазой и без газовой среды существовать не может, то в реальных условиях существование аэрозоля происходят различные процессы, которые характеризуются следующими параметрами.

Геометрические параметры пылевых частиц:

Физико – химические параметры:

Для удобства весь интервал возможных размеров делят на 3 группы:

λ _д – средняя длина свободного пробега молекулы газа λ _д = 0,065 = 0,07мкм

Наибольший интерес представляют частицы от 0,1 до 100 мкм. Частицы меньшего диметра находятся в области перехода о частиц к молекулам, или наоборот. Частицы крупнее 100 мкм долгое время находиться во взвешенном состоянии не могут.

Размер частиц определяется средним диаметром, который представляет собой сумму диаметров всех частиц, деленную на их полное число:

, число частиц.

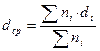
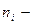
Т.к частицы, находящиеся в атмосфере имеют разные плотности и различную степень агрегации, то наиболее целесообразным считается определять размер частиц по их аэродинамическому поведению.

Стоксовский диаметр 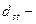диаметр сферической частицы, обладающей такой же скоростью оседания, что и рассматриваемая частица с плотностью равной плотности материала рассматриваемой частицы.

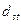
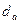
Стоксовский и аэродинамический диаметры отличаются друг от друга лишь тем, что зависит от плотности частицы, а не зависит.

Эквивалентный диаметр 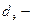размер частицы, на имеющей правильной формы объем которой равен объему рассматриваемой частицы.

Дисперсный состав удобно выражать:

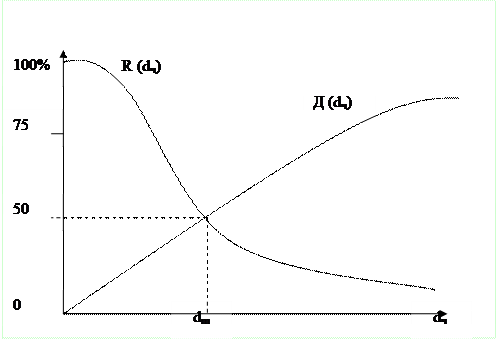
С помощью данной таблицы можно представить дисперсный состав в виде интегральных кривых R(dr), или D(dr), показывающих относительное содержание частиц с большими или меньшими размерами, чем заданные размеры.

d_m представляет собой размер, при котором масса частиц мельче d_m равна массе частиц крупнее d_m.

3. Графическое представление дисперсионного состава в виде дифференциальной кривой.

Для построения этой кривой процентное содержание каждой фракции делят на разность размеров частиц, принятых в качестве граничных, и это значение откладывают как ординаты точки, а абсцисса точек равна среднему размеру частиц соответствующей фракции.

Фракцией называют относительную долю частиц, размеры которой находятся в определенном интервале значений, принятых в качестве нижнего и верхнего предела (1– 3).По крупности все пыли условно делят на пять классов:

1 класс: наиболее крупнодисперсная пыль;

2 класс: крупнодисперсная пыль;

3 класс: среднедисперсная пыль;

4 класс: мелкодисперсная пыль;

5 класс: наиболее мелкодисперсная пыль.

4. Более полную и достоверную информацию о распределении частиц дает форма логарифмически-нормального распределения (ЛНР).

При построении интегральных кривых вероятностно в логарифмической системе координат графики строят особым способом.

В этой системе координат ось абсцисс начинается от точки, соответствующей значению равному 50%, и значение X откладывают: большие – вверх, меньшие – вниз от этой точки.

Если после построения графика линия получилось прямой, то это свидетельствует о логарифмически-нормальном характере распределения частиц, которое можно выражать с помощью параметров d_m и 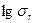— среднеквадратическое отклонение функции данного распределения. Оно находится из соотношения, которое является свойством интеграла вероятности:

Если кривая строится по проскоку D(dr), то

При ЛНР стандартное геометрическое отклонение 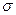представляет собой интервал размеров частиц, которые имеют 68,2% всех частиц данного объема. В этом случае среднее значение этого интервала:

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник

Количественные характеристики дисперсных систем

» data-shape=»round» data-use-links data-color-scheme=»normal» data-direction=»horizontal» data-services=»messenger,vkontakte,facebook,odnoklassniki,telegram,twitter,viber,whatsapp,moimir,lj,blogger»>

КОЛИЧЕСТВЕННЫЕ ХАРАКТЕРИСТИКИ ДИСПЕРСНЫХ СИСТЕМ в коллоидной химии

Коллоидная химия – это наука о физико-химических свойствах дисперсных систем и поверхностных явлениях. Вследствие исклю­чительно большой роли коллоидных систем и коллоидно-химичес­ких процессов в различных областях техники и человеческой дея­тельности и благодаря накоплению теоретического и практического материала, она выделилась в самостоятельную научную дисципли­ну. Объектами ее изучения являются гетерофазные системы, в ко­торых одна из фаз находится в высокодисперсном (раздробленном) состоянии.

Трудно назвать какую-либо сферу человеческой деятельнос­ти, в которой бы не использовались коллоидные системы или кол­лоидные процессы. Поверхностные явления (смачивание, адгезия, адсорбция, коагуляция, седиментация и др.) лежат в основе таких процессов химической технологии, как измельчение, гранулирова­ние, сушка, фильтрация, флотация, спекание, склеивание, краше­ние. К наиболее распространенным дисперсным системам относят дымы и туманы, эмульсии, пены, суспензии, порошки, ныли, гели. Дисперсными системами являются продукты питания, лекарства, биологоческие ткани. В мире каждый год производится сотни мил­лионов тонн дисперсных веществ и материалов. Знание закономер­ностей, присущих дисперсным системам, необходимо не только для оптимизации технологических процессов, но и при получении материалов с заданными свойствами, а также при решении задач охраны окружающей среды.

Определение размера частиц и удельной поверхности

Дисперсные системы всегда гетерогенные (гетерофазные). Они состоят из дисперсной фазы и дисперсионной среды.

Объектам изучения коллоидной химии присущи два основных признака:

Основные характеристики, используемые для описания дисперс­ных систем:

3. Удельная поверхность Sуд. – это межфазная поверхность (S1,2,), приходящаяся на единицу объема дисперсной фазы (V) или ее мас­сы (т).

Рассмотрим, как определяется удельная поверхность: если система состоит из п частиц, то

Коэффициенты формы для сферических, кубических частиц к = 6, для пленок к = 2, для волокон к = 4.

С увеличением дисперсности или уменьшением размера час­тиц возрастает удельная поверхность.

Методы получения дисперсных систем

Для получения дисперсных систем используют две группы ме­тодов: диспергационные и конденсационные (табл. 1.1).

Диспергирование – метод получения дисперсных систем пу­тем измельчения или дробления конденсированного тела.

Конденсация – метод получения дисперсных систем за счет объединения или агрегатирования молекул, или ионов вещества.

Дробление веществ до частиц малых размеров требует боль­шой затраты работы, так как поверхность раздела между фазами в таких системах весьма велика. Однако с помощью механических методов диспергирования даже в присутствии стабилизаторов прак­тически невозможно получение частиц с размерами менее 100 нм. В случае диспергирования одной жидкости в другой (несмешивающейся с первой) процесс называется эмульгирование.м. И в этом случае требуется почти обязательное присутствие в системе ве­ществ – эмульгаторов, стабилизирующих ее дисперсный состав (поверхностно-активных веществ, полимеров, порошков). Таким образом, обычно получают частицы радиусом не меньше 500 нм.

Более высокая дисперсность системы может быть достигнута при использовании мегодов, основанных на агрегации атомов и мо­лекул, т. е. методов конденсации. Именно эти методы чаще всего используются для получения истинно-коллоидных растворов.

Образование дисперсных систем при использовании конден­сационных методов происходит в результате либо гетерогенного зарождения, когда возникновение новой фазы осуществляется на уже имеющихся поверхностях (стенках сосуда, частицах посто­ронних веществ – ядрах конденсации), либо на поверхностях заро­дышей, возникающих самопроизвольно в гомогенной среде.

Зародыши в этом случае могут возникать лишь при определен­ном критическом пересыщении раствора.

Степень пересыщения

Самопроизвольное возникновение ядер конденсации зави­сит от многих причин: химических свойств реагирующих веществ, от характера ассоциации атомов и молекул, вязкости среды, темпе­ратуры и др.

Процесс образования дисперсной фазы при конденсации име­ет две основные стадии:

Дисперсность получаемых коллоидных систем зависит от соот­ношения скорости образования зародышей (υ1) и скорости их рос­та (υ2). При малой скорости образования зародышей (υ1 υ2) в системе, наоборот, возникает большое число мел­ких частиц. В этом случае образуются высокодисперсные золи, размер частиц в которых позволяет отнести их к коллоидным растворам.

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Определяем дисперсность системы D и удельную поверх­ность S уд

Рассчитываем общую поверхность частиц S и число частиц N в дисперсной системе.

Пример 1.2.

Пример 1.3.

Источник

Дисперсные системы

Количественные характеристики дисперсных систем

Дисперсные системы — это гетерогенные, преимущественно микро- гетерогенные системы, состоящие как минимум из двух фаз, одна из которых находится в дисперсном (раздробленном) состоянии. Обычно раздробленную (диспергированную) часть системы называют дисперсной фазой; непрерывную (сплошную), в которой находится раздробленная фаза, — дисперсионной средой.

Основная количественная характеристика — линейный (поперечный) размер частиц дисперсной фазы. Размерностью этой величины в системе СИ является метр, [а] = м, но поскольку речь идет об очень мелких частицах, то используются приставки микро-, нано- и другие (прил. Б). Для сферических частиц линейный размер — это диаметр (радиус) сферы, для кубических — длина ребра куба.

Раздробленность системы количественно характеризуют дисперсностью D — величиной, обратной линейному размеру, то есть D = —. Раз-

Дисперсные системы, имеющие частицы одинакового размера, называются монодисперсными; с неодинаковыми — полидисперсными. Реальные системы, как правило, полидисперсны, их свойства определяются степенью раздробленности вещества, а также характером распределения частиц по размерам.

Важным показателем дисперсной системы является удельная поверхность К0Т0 Р ая обычно выражается отношением суммарной по

верхности раздела дисперсной фазы 1 с дисперсионной средой 2 (межфазной поверхности) sj ₂ к суммарному объему этих частиц V:

Размерность удельной поверхности [$ ^] = м *, см 1 или мм

Поверхность может быть отнесена не только к объему частиц, но и к объему дисперсионной среды или системы в целом. В некоторых случаях удельную поверхность определяют как межфазную поверхность по отношению к массе дисперсной фазы т:

тогда ее размерность будет [s = м 2 /кг или см 2 /г.

Рассмотренные величины a, D и s ^ связаны между собой и для

частиц геометрически правильной формы эта связь имеет вид простых соотношений. Так, для монодисперсной системы, состоящей из сферических

частиц с диаметром d (г—радиус):

Для частиц кубической формы с ребром а:

Приведенные соотношения получены из геометрических формул, которые стоит напомнить:

объем шара с радиусом г (d = 2r):

поверхность шара: s=4m

поверхность одной грани куба с ребром а равна а 2 ;

В общем виде , где к — коэффициент формы

Для сферических и кубических частиц коэффициент формы равен 6, для геометрически неправильных частиц он может быть иным.

Частицы дисперсной фазы имеют разнообразную форму — сферическую, цилиндрическую, пластинчатую, округлую и др. Форма частиц зависит от метода получения дисперсной системы и от свойств составляющих ее фаз. Для примера на рис. 1.1 показаны фотографии частиц глин ряда месторождений Иркутской области — Трошковского (а), Никольского (б) и Слюдянского (в).

Рис. 1.1. Вид частиц глинистых минералов иод микроскопом

Фотографии получены с помощью сканирующего электронного микроскопа JIB Z 4 500. Видно, что частицы глины имеют различные размеры и сложную форму: чешуйчатую, пластинчатую, хлопьевидную со сложным рельефом поверхности и вкраплениями. В образцах существуют частицы с размерами от 1 до 60 мкм.

Величина удельной поверхности и многие свойства дисперсной системы зависят от формы частиц. Например, удельная поверхность порошков может колебаться от 0,01 до 10 м 2 /г в зависимости от размеров, формы частиц и микрогеометрии их поверхности.

С уменьшением линейных размеров частиц при дроблении и измельчении тел, а значит, с увеличением степени развитости их поверхности удельная поверхность существенно возрастает (табл. 1.1).

Удельная поверхность кубических тел

Рассмотренные количественные характеристики относятся к свободнодисперсным системам — системам с жидкой или газообразной дисперсионной средой.

Связнодисперсные (структурированные) системы отличаются от свободнодисперсных характером межчастичного взаимодействия. В них частицы дисперсной фазы связаны друг с другом за счет межмолекулярных сил, образуя своеобразные пространственные сетки или каркасы. Такие системы называются пористыми телами.

Для их количественных характеристик используют те же самые соотношения, но линейный размер характеризует величину мор. Кроме того, геометрической характеристикой связнодисперсных систем служит пористость П, равная отношению объема пор V_n к общему объему тела

Экспериментальное определение плотности и пористости тел проводят пикнометрически по стандартным методикам.

Если пористое тело имеет монодисперсную структуру, его удельную

поверхность легко оценить:

Чтобы определить удельную поверхность тела, образованного сферическими частицами одинакового размера, достаточно знать только радиус частиц. Если удельная поверхность рассчитывается на единицу массы тела, то надо знать еще и плотность вещества.

Приведенные соотношения справедливы и для определения параметров порошков, для которых иногда можно проводить аналогии с пористыми телами. Следует отметить, что приведенные формулы упрощены и не учитывают поверхность контакта частиц между собой — их количество может изменяться в зависимости от характера и плотности упаковки частиц в структуре пористого тела или порошка. С их учетом в формулах появляются коэффициенты, учитывающие долю таких контактов.

С уменьшением размеров частиц поверхность контакта увеличивается; для частиц с диаметром больше

100 нм сю можно пренебречь.

и удельная поверхность , где

п — число сферических пор в единице объема. Если поры имеют форму цилиндра, то

Удельную поверхность свободнодисперсной системы можно рассчитать, используя частичную концентрацию и (число частиц в 1 м 3 ) или п (число частиц в 1 кг вещества):

где Sq — поверхность шарообразной частицы дисперсной фазы радиусом г.

Частичная концентрация может быть, в свою очередь, выражена через объем V, и если , то в первом случае ,

при размерности м’ 1 ; во втором случае

при размерности = м 2 /кг.

Зная удельную поверхность s можно определить общую поверхность: . Для сферических частиц поверхность определится как , для кубических — как

Соотношения геометрических характеристик дисперсной системы представлены в двух небольших задачах.

Решение. Суммарный объем золота составляет , объем одной частицы кубической формы с длиной ребра а — Vq =а^. Тогда число частиц золота п в данной массе можно вычислить как или .Так как

, то длина нити L будет равна . В ре

зультате расчета получается:

Размерность полученной величины составляет

Решение. Удельная поверхность кубических частиц с длиной ребра / определяется как , или s ^ = 6D.

Общая поверхность, то есть поверхность всех коллоидных частиц: S=S yd’ V ’ rm

Так как поверхность будет покрыта только одной гранью коллоидных частиц, то . Проводим расчет: . Размерность полученной величины составляет

Геометрические параметры полидисперсных систем оценивают по кривым распределения частиц по размерам, которые показывают относительное количество частиц тех или иных размеров, диапазон размеров частиц, составляющих систему и др.

Существуют разнообразные методы изучения дисперсного состава системы (иначе методы дисперсионного анализа). Их разнообразие связано с тем, что свойства дисперсных систем существенно отличаются по агрегатному состоянию фаз, по межчастичному взаимодействию, по дисперсности.

В качестве примера в табл. 1.2 приведен гранулометрический состав глин, представленных на микрофотографиях на рис. 1.1.

Гранулометрический состав глин

Размер частиц, мкм, не более

Некоторые методы дисперсионного анализа дают сведения только о среднем размере частиц.

Понятие среднего размера частиц дисперсной системы требует особого пояснения. Например, в ситовом анализе размер частиц фракции после каждого сита принимается равным размеру соответствующих отверстий. В седименгационном анализе за средний принимается размер такой частицы, которая оседает со скоростью, одинаковой со скоростью оседания частиц монодисперсной системы. В общем случае под средним подразумевается такой размер, который равен размеру частиц монодисперсной системы, имеющий с данной полидиспсрсной системой общие параметры у и Z (х,у и Z —пространственные координаты).

Полную информацию об интервале дисперсности системы представляют интегральные и дифференциальные функции распределения частиц по размерам. В общем виде дифференциальная функция распределения

имеет вид: . Эта функция представляет собой число частиц

Ап с радиусами в интервале от до , отнесенное к общему

числу частиц всех размеров N и величине А/*, то есть долю общего числа частиц, приходящуюся на частицы в рассматриваемом интервале радиусов.

В зависимости от возможностей метода дисперсионного анализа дифференциальная функция распределения может представляться гистограммами, в которых высота столбцов отражает количество вещества в заданном интервале радиусов (не всегда одинаковые в разных областях размеров) или непрерывной линией на графиках при Аг —> 0 (рис. 1.2).

Интегральная функция распределения Q(r) связана с дифференциальной соотношением

и представляет долю общего числа частиц, приходящуюся на частицы с радиусом, большим некоторого значения г. По интегральным кривым распределения проще определять долю частиц, приходящихся на определенный интервал размеров Аг (она равна разности соответствующих значений Q(r + Ar)- Q(r).

Рис. 1.2. Дифференциальная кривая распределения

В зависимости от того, какие параметры измеряются в эксперименте, используются различные функции распределения (распределение по размерам, по поверхности и др.), в дальнейшем возможен пересчет от одних параметров к другим.

суммарное количество частиц) — на оси ординат.

В зависимости от свойств дисперсной системы график функции распределения частиц по размерам может иметь различную форму. Один из наиболее распространенных графиков — симметричная кривая Гаусса, которая характеризует закон нормального распределения. Кроме кривой Гаусса существуют другие виды кривых распределения.

Высокодисперсные системы (золи) подчиняются молекулярнокинетическим законам, позволяющим по экспериментальным данным определять размеры частиц дисперсной фазы.

Источник