Какие параметры определяются при обработке квд методом касательной
Обработка КВД по методу касательной
Процесс восстановления давления в конечной области КВД описывается формулой:

где ti – время замера после остановки скважины;
DP(ti) – разница между забойным давлением в момент замера и забойным давлением в момент остановки скважины:

i – угловой коэффициент, имеющий следующую структуру:

Коэффициент A в данном случае имеет следующую структуру:

Обработку КВД по методу касательной проводят в координатах DP(t) от Ln t. Через конечный участок проводят касательную до пересечения с осью ординат. В точке пересечения определяют значение коэффициента A. Значение коэффициента i определяют как тангенс угла наклона этой прямой (см. рисунок 4.2).
Рисунок 4.1 – Обработка КВД по методу касательной.
Из структуры коэффициентов A и i определяют фильтрационные параметры пласта:
Коэффициент гидропроводности пласта:

Зная толщину пласта h и вязкость нефти m, определяется коэффициент подвижности и проницаемость:


Относительная пьезопроводность пласта:

Приведенный радиус скважины:

Общее несовершенство вскрытия пласта – скин-фактор S:

Коэффициент продуктивности скважины на режиме перед остановкой:
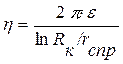
Время стабилизации режима работы скважины:

Исходные данные:
| Параметр | Значение | Размерность |
| Сжимаемость жидкости, βж | 0,0004 | 1/МПа |
| Сжимаемость горной породы, βг.п. | 0,00005 | 1/МПа |
| Пористость, m | 0,1 | д.е. |
| Толщина пласта, h | м | |
| Вязкость жидкости, µ | 0,7 | мПа*сек |
| Дебит работы скважины перед остановкой, Q | м 3 /сут | |
| Время работы скважины перед остановкой, T | сут | |
| Радиус скважины по долоту, rc | 0,1 | м |
| Максимальная погрешность определения конечного участка, d | 0,1 | д.е. |
| Радиус контура питания, Rк | м |
| Pзаб(t), бар | t, сек | Pзаб(t), бар | t, сек |
| 276,4 | 293,3 | ||
| 288,7 | 293,9 | ||
| 289,3 | 294,5 | ||
| 290,0 | 295,1 | ||
| 290,5 | 295,8 | ||
| 291,0 | 296,3 | ||
| 291,8 | 296,6 | ||
| 292,3 | 296,8 | ||
| 292,8 |
Порядок расчета:
1. По формуле (4.1) выбрать метод обработки КВД.
2. Построить КВД в координатах соответствующего метода обработки.
3. По графику КВД определить коэффициенты А и i
4. По формулам (4.11) – (4.17) определить фильтрационно-емкостные параметры пласта.
Лабораторная работа №5
«Исследование скважин методом гидропрослушивания»
Методы обработки кривой КВД



Метод снятия кривой восстановления давления.
Рис. 7.1. Схема снятия КСД- КВД
Метод снятия кривой восстановления давления (КВД) после закрытия скважины позволяет определить проводимость, пьезопроводность, пористость пласта, а также выявить зоны с резко выраженной неоднородностью, находящиеся в области дренирования скважины.
Перед началом исследования методом КВД скважина должна работать с некоторым установившимся дебитом и забойным (устьевым) давлением. Если скважина перед закрытием на снятие КВД работала с частой сменой неустановившихся режимов, то необходимо фиксировать указанные параметры на всех режимах работы и остановок, предшествующих снятию КВД. После этого закрывают скважину и регистрируют изменение давления на забое (устье), а также изменение температуры газа. Чтобы избежать влияние процессов в стволе скважины на форму КВД, желательно проводить замеры КВД на забое с помощью глубинных приборов.
Для обработки КВД существует несколько методов. При решении уравнения, описывающего процесс восстановления давления, используется два вида условий: бесконечный пласт и ограниченный пласт с постоянным давлением на контуре. Формулы, полученные для бесконечного пласта, применяются в тех случаях, когда в процессе исследования скважины, границы области дренирования не сказываются на поведении этой скважины.
Метод обработка КВД для бесконечного пласта в зависит от условий работы скважины до остановки. Если время работы скважины Т до снятия КВД больше времени восстановления давления t (T ³ t), КВД обрабатывается по формуле:
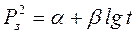
где, Рз(t) – давление на забое скважины, МПа; t – текущее время восстановления давления, сек; a иb – коэффициенты.
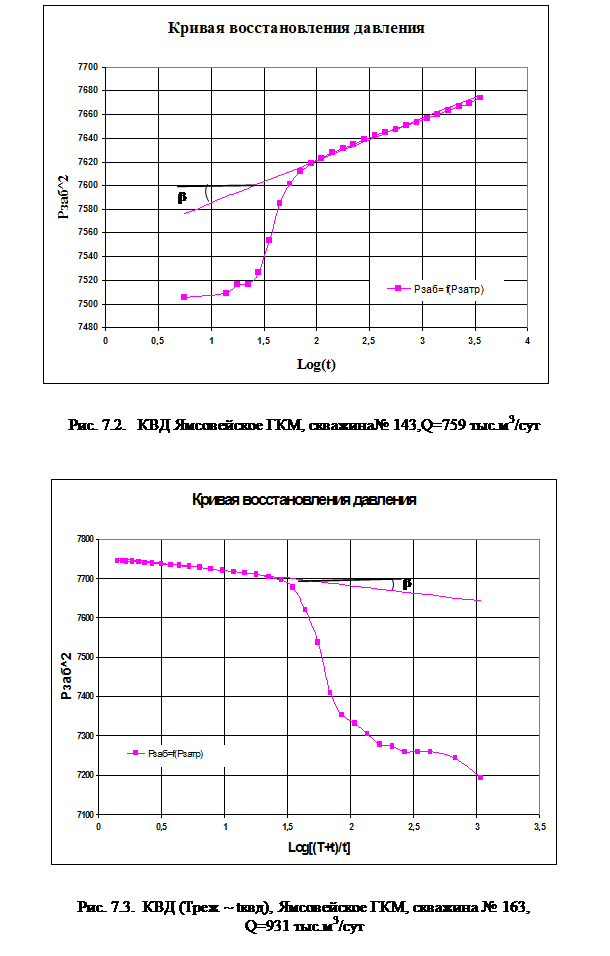
КВД строят в координатах Р 2 з от lg t (рис.6.2) и по графику определяют коэффициенты a и b. Для этого выделяют на графике прямолинейный участок и проводят к нему касательную прямую. Тангенс угла наклона касательной равен b, а отрезок, отсекаемый касательной на оси ординат, равен a. По найденным a и b рассчитывают параметры пласта. Параметр проводимости пласта рассчитывают по формуле:
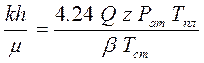
Если время работы скважины Т до снятия КВД меньше времени восстановления давления t (T £ t), КВД обрабатывается по формуле:
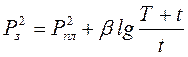
где, T – время работы скважины перед снятием КВД; РПЛ – пластовое давление.
Применение формулы (6.1) в этом случае искажает конечный участок КВД и может привести к ошибочным результатам при расчете параметров пласта.
КВД строят в координатах P 2 З от lg [(T + t) / t)] и по углу наклона прямолинейного участка определяют коэффициент b (рис.6.3). Метод позволяет определить пластовое давление. Для этого надо продолжить КВД до значения lg [(T + t) / t)] = 0 и точка пересечения прямой с осью P 2 З даст значение квадрата пластового давления.
 |
Если в процессе исследования скважины на ее поведении сказываются условия на границе пласта, то обработка КВД проводится по формуле для ограниченного пласта
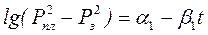
Методика обработки кривых восстановления давления, полученных при исследовании газовой скважины
Категории
Обработка кривой восстановления давления проводится в следующей последовательности:
Вычисление производной от изменения забойного давления (депрессии)
p(t) – забойное давление зарегистрированное после остановки скважины, ат
p(0) – забойное давление в скважине до ее остановки, ат
t – время восстановления забойного давления с момента остановки скважины, сек
Построение графика кривой восстановления давления в логарифмических координатах log(dp)-log(t); и ее производной в логарифмических координатах log(D) – log(t).
Определение участка постоянной производной на диагностическом графике, который показывает наступление радиальной фильтрации флюида при нестационарном изменении давления в скважине.
По участку постоянной производной впоследствии определяют параметры пласта и скважины.
Обработка
Обработка кривой восстановления давления по схеме бесконечного пласта методом Миллера, Дайеса, Хетчинсона (MDH) – метод касательной.
Известно, кривая восстановления давления в газовой скважине, вскрывшей однородный бесконечный пласт при мгновенном изменении дебита, при достаточно большом периоде работы скважины до остановки по сравнению с периодом исследования (при T >> t), за исключением самых начальных участков, описывается формулой (MDH)
где: рсо – установившееся забойное давление до остановки скважины, ат;
рс(t) – изменение забойного давления после остановки скважины, ат;
Tпл – пластовая температура, °К; Tст =293°К; zпл – коэффициент сверхсжимаемости газа при пластовых условиях;
«b» – коэффициент двучленной формулы определяется по индикаторной диаграмме.
Перестраивая кривую восстановления давления в координатах Δр,ln(t), по асимптоте определяют параметры: гидропроводность kh/m и приведенную пьезопроводность
Не учитывая нарушение линейного закона фильтрации вблизи скважины (турбулентность потока) введением коэффициента «b» в уравнение (4), величина приведенной пьезопроводности будет равна
После определения параметров пласта
После определения параметров пласта по формулам (3-5) обработку кривой восстановления давления проводят по схеме пласта конечных размеров с постоянным давлением на контуре (дифференциальный метод Чарного) по формуле
Перестраивая кривую восстановления давления в координатах по прямолинейному участку определяем параметры гидропроводности kh/m и параметр
Перестраивая кривую восстановления давления в координатах 
Участок временного интервала для определения параметров выбирается так, чтобы величина определяемой гидропроводности была равна величине гидропроводности, определенной по схеме бесконечного пласта (MDH)
Определяем фильтрационное сопротивление
в формуле (10) величины χ/r 2 cпр χ/R 2 k вычислены выше по формулам (5), (9).
Из формулы (9) можно вычислить величину Rk, определив предварительно величину пьезопроводности χ по формуле (15).
Обработка методом Хорнера
Обработка методом Хорнера позволяет определить пластовое давление.
Параметры пласта следует определять по тому же участку преобразованной в полулогарифмических координатах КВД, что и методом MDH (касательная).
Если период работы скважины до ее остановки на исследование T соизмерим с периодом наблюдения t после остановки, обрабатывать такие кривые восстановления давления следует методом Хорнера по формуле
где Т – время (сек) работы скважины до остановки на исследование с дебитом Q (см 3 /сек)
Перестраивая кривую восстановления давления в координатах [p 2 (t) – log(T+t/t)], по асимптоте определяют параметр гидропроводности kh/μ.
Метод Хорнера не позволяет определить параметр приведенной пьезопрводности c/r 2 cпр, но дает возможность определить пластовое давление pпл.
Оценка состояния призабойной зоны скважины
Величину скин-эффекта определяют по формуле
Определение фактического коэффициента
Определение фактического коэффициента продуктивности скважины по формуле:
В формуле (16) величина гидропроводности kh/m определена из обработки кривой восстановления давления методом MDH (формула 3).
Фильтрационное сопротивление фактическое 
Вычисление фактического дебита скважины для определения достоверности полученных параметров производят по формуле:
В формулы (16), (17) входит интегральное значение скин-эффекта, т.е. – псевдоскин.
Радиус дренирования Rдр (радиус контура Rk) за время исследования скважины вычисляют по формуле: Rдр = √2,25χT, (18)
где χ – величина пьезопроводности определена выше (формула 15),
T – продолжительность КВД, сек,
Δр = рсо 2 – рс(t) 2 – определено в конце исследования.
Потенциальный дебит
Потенциальный дебит скважины может быть вычислен по формуле (17) при условии снижения скин-эффекта (псевдоскина) до «0».
Можно задавать разные значения скина от 0 до 2,3, и т.д.
Величине радиуса дренирования Rдр также можно задавать разные значения от полученного при обработке КВД (формула 18) до радиуса контура питания, равного половине расстояния между скважинами Rk.
Пример обработки кривой восстановления давления
В качестве примера приведены результаты исследования скважины №1074.
До остановки скважина работала с дебитом q = 490 тыс.м 3 /сут. Кривая восстановления давления зарегистрирована в течение 2,5 час.
Обработка кривой восстановления давления проведена в следующей последовательности:
Диагностирование кривой восстановления давления
Определен участок постоянной производной на диагностическом графике (6,94 – 8,2), который показывает наступление радиальной фильтрации флюида при нестационарном изменении давления в скважине.
Методами MDH и Хорнера определены параметры пласта – гидропроводность, пьезопроводность, фильтрационное сопротивление – скин-эффект, фактический коэффициент продуктивности скважины и пластовое давление. Участок для определения параметров установлен по графику диагностики.
Приведённый КВД построен в координатах dp, ln(t).
Обработка кривой восстановления давления по схеме ограниченного пласта с постоянным давлением на контуре Рк=const (дифференциальный метод)
Участок временного интервала для определения параметров выбирается так, чтобы величина определяемой гидропроводности была равна величине гидропроводности, определенной по схеме бесконечного пласта (MDH).
Обработка методом Хорнера
Обработка методом Хорнера выполнена по формуле (11). На данном режиме скважина работала 6,4 часа. На приведены результаты обработки КВД методом Хорнера.
Параметр гидропроводности и величина пластового давления определены по тому же временному участку, что и методом MDH.
Рпл = 245,0 ат – пластовое давление вычислено по формуле (12).
Оценка состояния призабойной зоны скважины
По известным параметрам пласта определены фактический коэффициент продуктивности скважины и скин-эффект.
Скин-эффект вычислен по формуле (13).
Sk = 6,2 χ/r 2 спр = 4,95х10 6 1/сек, χ = 2570 см 2 /сек, rспр = 0,023 см – несовершенство скважины по степени и характеру вскрытия. Нелинейность (турбулентность) потока вблизи ствола скважины учтена в формуле (4).
Определение фактического и потенциального коэффициентов продуктивности
Фактический коэффициент продуктивности определен по формуле (16)
Kфакт = 47,2 м 3 /сут.ат 2 при Rдр/rc = 656, Rдр = 72,1 м, Sk = 23.
Проведена проверка заданной величины дебита скважины по формуле (17), в которой kh/μ = 5383 дсм/спз, Rдр = 72,1 м, rc = 0,11м, Sk = 23, ∆р = 10299 ат 2 Qфакт = 486 тыс.м 3 /сут.
Потенциальный коэффициент продуктивности и потенциальный дебит скважины может быть определен по формулам (16), (17) соответственно при следующих условиях:
Кроме этого, при оценке потенциальных возможностях скважины можно менять величину депрессии ∆р.
В таблице 1 приведены исходные данные и результаты обработки кривой восстановления давления.
Совмещение фактической
Совмещение фактической и расчетной кривых восстановления давления.
С целью определения достоверности параметров пласта и скважины, полученных в результате интерпретации кривой восстановления давления, вычислена теоретическая кривая восстановления давления и совмещена с фактической кривой.
Вычисления выполнены по формуле (1) с параметрами гидропроводности (kh/μ) и приведенной пьезопроводности (χ/r 2 спр), определенными выше, т.е. теоретическая КВД вычислена с общим интегральным скин-эффектом (псевдо-скином).
Получены хорошие результаты совмещения фактической и теоретической кривых восстановления давления, приведенные на (тонкие сплошные линии) на всех этапах обработки КВД.
Добыча нефти и газа
Изучаем тонкости нефтегазового дела ВМЕСТЕ!
Методы обработки квд
Факторы, влияющие на методику обработки КВД. Методика обработки КВД существенным образом зависит от темпа нарастания давления после остановки скважины, наличия соседних скважин и расстояния между ними.
Если исследуемая скважина удалена от соседних работающих на 3-4км и продолжительность её работы незначительна, то данную скважину можно рассматривать в “бесконечном “ пласте. В противном случае процесс восстановления давления надо рассматривать как процесс, происходящий в пласте конечных размеров.
А) Методика обработки КВД в условиях “бесконечного” пласта
а) Значительное время работы скважины (рис. 3.7)
Используемая зависимость.


По полученным значениям a и b определяют следующие параметры пласта:
· параметр проводимости 
· при известной эффективной мощности значение проницаемости 
· при известном коэффициенте b параметр
Методы обработки КВД alt=3.3.1.2. Методы обработки КВД src=
images\3-3-1-2-metody-obrabotki-kvd_8.png width=314 height=67 /;
· для совершенной скважины: коэффициент пьезопроводности пласта

и параметр скин-эффекта, характеризующий совершенство скважины и состояние призабойной зоны

если С 0, то призабойная зона имеет дополнительное сопротивление. При сравнении значений коэффициентов С по различным скважинам можно судить о качестве вскрытия в той или иной скважине и намечать мероприятия по интенсификации притока.
Используемая зависимость.
Б) Методика обработки КВД в условиях “конечного” пласта
Уравнение КВД. Для пласта конечных размеров используется формула

Параметры пласта определяются из найденных коэффициентов a1 и b1. По коэффициенту a1 можно найти b и, следовательно, параметры 

Какие параметры определяются при обработке квд методом касательной
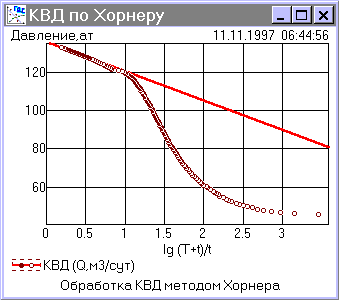
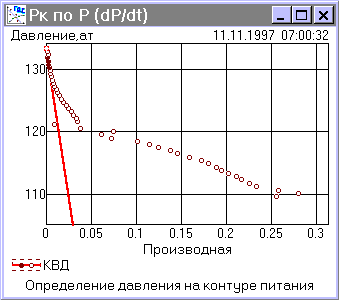
В зависимости от технологии проведения испытаний, КВД могут обрабатываться методами Хорнера (после непродолжительного притока, недостаточного для полного формирования воронки депрессии и установления стационарного режима) или касательной (после длительной работы на установившемся режиме). Эти методы позволяют рассчитать коэффициент гидропроводности удаленной зоны пласта, оценить состояние прискважинной зоны (скин-фактор и коэффициент призабойной закупорки), а метод Хорнера позволяет также определить текущее пластовое давление.
Пользователь может непосредственно на графике выбрать участок кривой для обработки, при необходимости скорректировать положение линии регрессии. Выбирая различные участки кривых, можно оперативно сравнить результаты различных вариантов обработки, оценить параметры участков пласта различной удаленности от скважины.
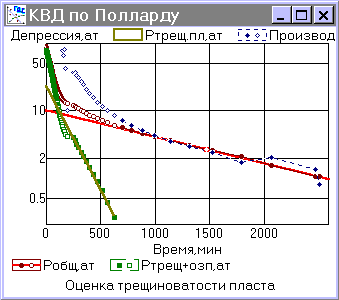
Представленная на рисунке графоаналитическая методика обеспечивает поэтапное выделение этих составляющих депрессии по КВД.
В результате по соотношению составляющих депрессии рассчитывается коэффициент динамической емкости, который позволяет оценить долю пустотности, приходящуюся на трещинную систему пласта. Таким образом, определяется соотношение первичной (межгранулярной) и вторичной (трещинной и кавернозной) пористости. Кроме того, метод Полларда дает оценку истинной проницаемости трещин, величины скин-эффекта и коэффициента заканчивания скважины.
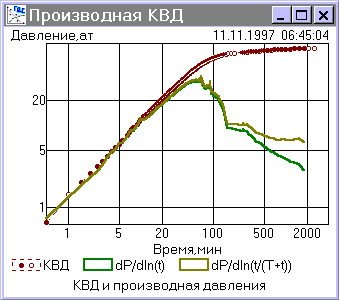
Для определения модели пласта и режима фильтрации в последнее время практикуют построение графиков давления и производной давления в билогарифмических координатах. Для дифференцирования КВД применяется специальный алгоритм с переменной степенью сглаживания. Пользователь может регулировать степень сглаживания, чтобы получать незашумленные и неискаженные кривые производной при различных временных интервалах и качестве замеров давления. Также можно оперативно исключить из расчетов отдельные недостоверные точки или участки кривых. Такие интерактивные манипуляции позволяют получить качественную кривую производной.
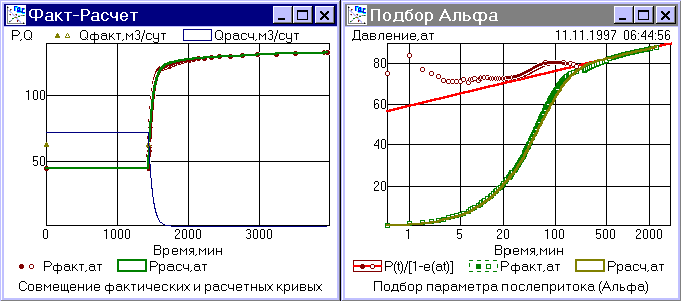
В нашей системе для учета “послепритока” используется модель, предполагающая экспоненциальный характер затухания дебита “послепритока” после закрытия скважины. Такая модель приемлема в большинстве случаев и позволяет избежать значительных погрешностей, которые возникают при попытках оценить “послеприток” дифференцированием фактических кривых. Автоматическим подбором показателя затухания дебита ( Альфа ) добиваются линейности кривой, исправленной за “послеприток”, на всем протяжении, включая ранние и поздние времена. Чтобы оценить качество обработки, модельная кривая (рассчитанная по определенным параметрам пласта и “послепритока”) совмещается с фактическими замерами.