Какие параметры цилиндрической зубчатой передачи стандартизованы
Основные геометрические параметры цилиндрических зубчатых колёс
Рассмотрим случай прямозубых (эвольвентных) зубчатых колёс без корригирования (с несмещённым исходным контуром)
Стандартизованными параметрами, характеризующими зубчатую передачу являются:
Значения этих параметров приведены в таблице 1 вместе с предлагаемыми системами номограмм для графоаналитического выбора основных геометрических, в том числе стандартизованных, параметров зубчатой пары:
– количества зубьев колеса и шестерни,
– делительных диаметров (начальных диаметров),
– диаметров вершин зубьев,
– диаметров оснований зубьев.
| Передаточные числа, m | Межосевые расстояния,Номограммы для определения параметров эвольвентных цилиндрических зубчатых передач без смещения исходного контура c внешним зацеплениемZ1 = 10. 60 Z2 = 15. 90 i = 1. 8 A = 40. 710 мм d1=0. 500 мм m = 0.1. 45 d2=0. 1000 мм m = 0.1. 60 Z1 = 10. 35 Z2 = 10. 60 i = 1. 5.5 A = 63. 280 мм d1=50. 300 мм m = 1.5. 28 d2=50. 300 мм m = 1.5. 28 Z1 = 10. 35 Z2 = 10. 60 i = 1. 5.5 A = 280. 710 мм d1=300. 550 мм m = 9. 45 d2=200. 950 мм m = 3.5. 80 Обозначения параметров, представленных на номограммах: Высота зуба h (мм) и радиальный зазор C (мм) определяем по таблице 3 (ниже по тексту) в зависимости от значения модуля Передаточное число i равно отношению чисел зубьев колеса Z2 и шестерни Z1: Геометрические зависимости | ||
 | |||
Ниже приведена таблица 3 значений высоты зуба и радиального зазора в зависимости от модуля.
h, мм
Прямозубые цилиндрические зубчатые колёса со смещённым исходным контуром
Рассмотрим корригирование прямозубых зубчатых передач в соответствии со стандартами, действовавшими до 1970 г.
Корригирование рекомендуется для цилиндрических и конических передач при условии неравенства количества зубьев шестерни Z1 и колеса Z2.
Наиболее целесообразно применять корригирование в следующих случаях:
Высотное корригирование.
Внешний диаметр шестерни увеличивается на величину 2·х·m (положительное смещение), внешний диаметр колеса уменьшается на величину 2·х·m (отрицательное смещение). Значение х выбирается по таблице. При положительном смещении увеличивается длина головки зуба, длина ножки соответственно уменьшается. При отрицательном смещении наоборот. Величины делительных диаметров и межосевое расстояние остаются неизменными.
Величина смещения исходного контура колеса указывается в таблице на чертеже зубчатого колеса
При корригировании зубчатого колеса рассчитывается размер зуба при измерении по постоянной хорде sx (толщина зуба по делительноой окружности) и высота зуба hx. При положительном смещении sx увеличивается, зу утолщается у основания и упрочняется.
Значение коэффициентов смещения Х1=-Х2 выбираются по материалам источников 1930-x гг. (при профильном угле исходного контура 20 0 и коэффициенте высоты головки зуба, равном 1)
ТЕРМИНЫ, ОПРЕДЕЛЕНИЯ И ОБОЗНАЧЕНИЯ
Прямозубое зубчатое колесо (черт. 2).
Косозубое зубчатое колесо
Цилиндрическое зубчатое колесо с винтовыми зубьями, теоретические линии которых эквидистантны и на развертке соосной цилиндрической поверхности являются параллельными прямыми (черт. 3).
Шевронное зубчатое колесо
Цилиндрическое зубчатое колесо, венец которого по ширине состоит из участков с правыми и левыми зубьями (черт. 4).
1. Различают шевронное и многошевронное цилиндрическое зубчатое колесо, состоящее соответственно из двух и более полушевронов.
2. Различают шевронное цилиндрическое зубчатое колесо со сплошным венцом и разделенными полушевронами.
Часть венца шевронного цилиндрического зубчатого колеса, в пределах которого линии зубьев имеют одно направление.
Цилиндрическое зубчатое колесо, теоретические линии зубьев которого на развертке делительной поверхности отличны от прямых (черт. 5).
Цилиндрическое зубчатое колесо с криволинейными зубьями, теоретическими линиями которых на развертке делительной поверхности являются дуги окружностей.
Зубчатое колесо, зубья которого образованы при номинальном положении исходной производящей рейки, характеризуемом отсутствием касания (касанием) делительных поверхностей исходной производящей рейки и обрабатываемого зубчатого колеса (черт. 6).
Колесо с положительным (отрицательным) смещением
Зубчатое колесо со смещением, при котором делительная плоскость исходной производящей рейки не пересекает (пересекает) делительный цилиндр обрабатываемого зубчатого колеса (черт. 19).
Эвольвентное зубчатое колесо
Цилиндрическое зубчатое колесо, теоретические торцовые профили зубьев которого являются эвольвентными, образуемыми как траектории точек прямой, перекатываемой без скольжения по окружности.
Циклоидальное зубчатое колесо
Цилиндрическое зубчатое колесо, теоретические торцовые профили зубьев которого являются циклическими кривыми, образуемыми как траектории точек, связанных с окружностью, перекатываемой без скольжения по другой окружности.
Циклоидальное цилиндрическое зубчатое колесо, зубья которого выполнены в виде цилиндрических штифтов с осями, параллельными оси зубчатого колеса.
Цилиндрическая зубчатая передача, одним из звеньев которой является зубчатая рейка (черт. 7).
Цилиндрическая зубчатая передача, зубчатые колеса которой прямозубые.
Цилиндрическая зубчатая передача, зубчатые колеса которой косозубые.
Цилиндрическая зубчатая передача, зубчатые колеса которой шевронные.
Передача без смещения
Зубчатая передача, у которой оба зубчатых колеса без смещения.
Передача со смещением
Зубчатая передача, у которой, по крайней мере, одно зубчатое колесо со смещением.
Зубчатая передача со смещением, сумма (для внешнего зацепления) или разность (для внутреннего зацепления) смещений которой равны нулю.
Положительная (отрицательная) передача
Зубчатая передача со смещением, сумма или разность смещений которой больше (меньше) нуля
Цилиндрическая зубчатая передача, зубчатые колеса которой эвольвентные.
Цилиндрическая зубчатая передача, зубчатые колеса которой циклоидальные.
Циклоидальная цилиндрическая передача, в которой одно из зубчатых колес цевочное.
2. Элементы и параметры цилиндрического зубчатого колеса
Делительный (начальный) цилиндр
Делительная (начальная) поверхность цилиндрического зубчатого колеса
Делительный нормальный модуль зубьев цилиндрического зубчатого колеса, принимаемый в качестве расчетного и равный модулю нормального исходного контура.
Наибольшее расстояние между торцами зубьев цилиндрического зубчатого колеса по линии, параллельной его оси (черт. 8).
Длина общей нормали
Расстояние между разноименными боковыми поверхностями зубьев цилиндрического зубчатого колеса по общей нормали к этим поверхностям (черт. 9).
Число зубьев цилиндрического зубчатого колеса, размещающихся в длине общей нормали
Расстояние между поверхностями двух цилиндрических роликов (шариков) по общей нормали к поверхностям, касающимся главных боковых поверхностей зубьев, при этом в торцовом сечении оси симметрии впадин, в которых лежат ролики (шарики), составляют углы, равные 180° и 180° 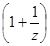
Расстояние между окружностями вершин зубьев и впадин цилиндрического зубчатого колеса (черт. 12).
Высота головки (ножки)
Расстояние между делительной окружностью цилиндрического зубчатого колеса и его окружностью вершин (впадин) (черт. 12).
Расстояние между окружностью вершин зубьев цилиндрического зубчатого колеса и концентрической окружностью, проходящей через граничные точки профилей зубьев (черт. 12).
Кратчайшее расстояние от вершины зуба цилиндрического зубчатого колеса до средней точки толщины по хорде (черт. 13).
Высота модификации головки (ножки)
Расстояние между концентрическими окружностями, проходящими соответственно через начальные точки линии модификации головок (ножек) и через точки притупления продольных кромок зубьев (граничные точки профилей зубьев) (черт. 14).
3. Сечения и параметры зубчатой рейки
Сечение зубчатой рейки плоскостью, нормальной к теоретическим линиям ее зубьев (черт. 15).
Сечение зубчатой рейки в реечной передаче плоскостью, перпендикулярной оси парного зубчатого колеса (черт. 15).
Сечение косозубой зубчатой рейки в реечной передаче плоскостью, перпендикулярной ее делительной плоскости и содержащей ось парного зубчатого колеса или параллельной ей (черт. 15).
Прямая, принадлежащая делительной плоскости рейки или параллельной ей плоскости.
1. Различают делительную, начальную и другие образующие плоскости рейки, принадлежащие соответственно ее делительной, начальной и другим параллельным плоскостям, и торцовую, осевую и нормальную образующие плоскости рейки, принадлежащие соответственно ее торцовому, осевому и нормальному сечениям.
2. При образовании терминов видовых понятий торцовой, осевой, нормальной и других образующих плоскости рейки к термину родового понятия добавляется слово, определяющее делительную, начальную и другие образующие плоскости рейки, например «начальная торцовая образующая плоскости рейки».
Торцовый (осевой, нормальный) шаг
Расстояние между одноименными поверхностями соседних зубьев рейки по ее торцовой (осевой, нормальной) образующей (черт. 15).
Торцовая (осевая, нормальная) толщина
Расстояние между разноименными поверхностями зуба рейки по ее торцовой (осевой, нормальной) образующей (черт. 15).
Торцовая (осевая, нормальная) ширина впадины
Расстояние между ближайшими разноименными поверхностями соседних зубьев рейки по ее торцовой (осевой, нормальной) образующей (черт. 15).
Число зубьев рейки
Число зубьев, расположенных на зубчатой рейке.
Острый угол между линией зуба рейки и ее осевой образующей (черт. 15)
Острый угол в выбранном плоском сечении между касательной к профилю зуба рейки в данной точке и прямой, перпендикулярной к делительной плоскости рейки.
4. Исходный и исходные производящие контуры и их параметры
Очертание зубьев номинальной исходной зубчатой рейки в сечении плоскостью, перпендикулярной ее делительной плоскости (черт. 16).
Образующая плоскости номинальной исходной зубчатой рейки, лежащая в плоскости ее исходного контура (черт. 16).
Исходные контуры пары номинальных исходных зубчатых реек, соответствующих одному и тому же сечению этих реек (черт. 17).
Примечани е. Различают пары торцовых, осевых и нормальных исходных контуров, соответствующие торцовому, осевому и нормальному сечению пары номинальных исходных зубчатых реек.
Пара исходных контуров, один из которых является копией другого (черт. 18)
Расстояние между прямыми вершин зубьев пары исходных контуров при относительном положении, определяемом совпадением делительных прямых при введении зубьев одного контура во впадины другого (черт. 18).
Расстояние между прямыми вершин зубьев и впадин пары исходных контуров при их относительном положении, определяемом совпадением делительных прямых при введении зубьев одного контура во впадины другого (черт. 18).
Очертание зубьев номинальной исходной производящей рейки в сечении плоскостью, перпендикулярной ее делительной плоскости.
Исходные производящие контуры пары номинальных исходных производящих реек, соответствующие одному и тому же сечению этих реек.
Примечани е. Различают пары торцовых, осевых и нормальных исходных производящих контуров, соответствующие торцовому, осевому и нормальному сечениям пары номинальных исходных производящих реек.
Расстояние по нормали между делительной поверхностью цилиндрического зубчатого колеса и делительной плоскостью теоретической исходной зубчатой рейки при ее номинальном положении (черт. 19).
Примечани е. Смещение исходного контура принимается положительным, если делительная плоскость не пересекает делительной поверхности зубчатого колеса, и отрицательным, если пересекает ее.
Расстояние по нормали между делительной поверхностью цилиндрического зубчатого колеса и делительной плоскостью номинальной исходной производящей рейки при ее номинальном положении.
Примечание. Смещение исходного производящего контура равно смещению исходного контура.
Отношение смещения исходного контура к нормальному модулю цилиндрического зубчатого колеса.
Смещение исходного производящего контура, соответствующее такой номинальной толщине зубьев цилиндрического зубчатого колеса, при уменьшении которой возникает подрезание зубьев этого зубчатого колеса данным производящим колесом.
Коэффициент наименьшего смещения
Отношение наименьшего смещения исходного контура к нормальному модулю цилиндрического зубчатого колеса
Примечани е. При отсутствии дополнительных указаний имеется в виду коэффициент наименьшего смещения, соответствующий станочному зацеплению с номинальной исходной производящей рейкой.
Наименьшее число зубьев
Наименьшее число зубьев для зубчатых колес одного и того же исходного контура с заданным смещением, при котором еще отсутствует подрезание зубьев данным производящим колесом.
5. Параметры цилиндрической передачи
Длина отрезка межосевой линии цилиндрической зубчатой передачи, заключенного между окружностями вершин зубьев шестерни и колеса (черт. 20).
Рабочая ширина венца
Общая часть ширины венцов зубчатых колес цилиндрической передачи, в пределах которой глубина захода зубьев постоянна (черт. 20).
Высота начальной головки (ножки)
Расстояние между начальной окружностью и окружностью вершин (впадин) цилиндрического зубчатого колеса (черт. 21 ).
Делительное межосевое расстояние
Межосевое расстояние цилиндрической зубчатой передачи, равное полусумме делительных диаметров зубчатых колес при внешнем зацеплении или полуразности при внутреннем зацеплении
Угол торцового перекрытия
Угол поворота зубчатого колеса цилиндрической передачи от положения входа в зацепление торцового профиля его зуба до выхода из зацепления (черт. 22).
Угол дополюсного (заполюсного) перекрытия
Угол поворота зубчатого колеса цилиндрической передачи, соответствующий взаимодействию активных торцовых профилей начальной ножки (головки) зуба ведущего и начальной головки (ножки) ведомого зубчатых колес (черт. 22).
Угол осевого перекрытия
Угол поворота зубчатого колеса косозубой цилиндрической передачи, при котором общая точка контакта зубьев переместится по линии зуба этого зубчатого колеса от одного из торцов, ограничивающих рабочую ширину венца, до другого (черт. 23).
Коэффициент торцового перекрытия
Отношение угла торцового перекрытия зубчатого колеса цилиндрической передачи к его угловому шагу.
Коэффициент дополюсного (заполюсного) перекрытия.
Отношение угла дополюсного (заполюсного) перекрытия зубчатого колеса цилиндрической передачи к его угловому шагу.
Коэффициент осевого перекрытия
Отношение угла осевого перекрытия зубчатого колеса косозубой цилиндрической передачи к его угловому шагу.
Разность межосевого расстояния цилиндрической зубчатой передачи со смещением и ее делительного межосевого расстояния (черт. 24).
Отношение воспринимаемого смещения к нормальному модулю цилиндрического зубчатого колеса.
Сумма (разность) смещений исходного контура у колеса и шестерни цилиндрической зубчатой передачи внешнего (внутреннего) зацепления
Отношение суммы (разности) смещений к нормальному модулю цилиндрического зубчатого колеса
Разность между суммой или разностью смещений и воспринимаемым смещением
Отношение уравнительного смещения к нормальному модулю цилиндрического зубчатого колеса.
6. Элементы и параметры эвольвентной цилиндрической зубчатой передачи
Окружность, развертка которой является теоретическим торцовым профилем зуба эвольвентного цилиндрического зубчатого колеса (черт. 25).
Соосная цилиндрическая поверхность эвольвентного цилиндрического зубчатого колеса, торцовое сечение которой является основной окружностью (черт. 25).
Диаметр основной окружности эвольвентного зубчатого колеса
Угол между радиусами-векторами, проведенными из центра концентрической окружности эвольвентного цилиндрического зубчатого колеса, соответственно, в предельную, принадлежащую основной окружности, и рассматриваемую точки теоретического торцового профиля зуба.
Угол между нормалями к теоретическому торцовому профилю зуба эвольвентного цилиндрического зубчатого колеса в его предельной, принадлежащей основной окружности, и рассматриваемой точках.
Основной угол наклона
Угол наклона линии зуба эвольвентного косозубого цилиндрического зубчатого колеса на его основном цилиндре.
Основной окружной шаг
Окружной шаг эвольвентного цилиндрического зубчатого колеса по основной окружности
Основной нормальный шаг
Нормальный шаг зубьев эвольвентного цилиндрического зубчатого колеса по его основному цилиндру
Линейная величина, в π раз меньшая основного окружного шага зубьев эвольвентного цилиндрического зубчатого колеса
Основной нормальный модуль
Линейная величина, в π раз меньшая основного нормального шага зубьев эвольвентного цилиндрического зубчатого колеса
Расстояние по контактной нормали в эвольвентном зацеплении между двумя контактными точками одноименных главных поверхностей соседних зубьев цилиндрических зубчатых колес.
Нормальный боковой зазор
Боковой зазор зубчатой передачи при линейном контакте зубьев сопряженных зубчатых колес, определяемый в эвольвентной передаче по нормали к общим линиям контакта зубьев (черт. 26)
Поверхность зацепления эвольвентной цилиндрической передачи
Острый угол в главном сечении эвольвентной цилиндрической зубчатой передачи между линией зацепления и прямой, перпендикулярной к межосевой линии
Длина части активной линии зацепления, соответствующая углу дополюсного (заполюсного) перекрытия зубчатого колеса эвольвентной передачи (черт. 27)
Номинальная толщина зуба, которая у эвольвентного цилиндрического зубчатого колеса равна теоретической толщине зуба
Отрезок прямой, соединяющий две точки разноименных эвольвентных боковых поверхностей зуба цилиндрического зубчатого колеса, принадлежащие одной цилиндрической соосной поверхности и нормалям, приведенным к ним из одной точки делительной поверхности (черт. 28).
Отрезок прямой, соединяющий две точки разноименных эвольвентных боковых поверхностей соседних зубьев цилиндрического зубчатого колеса, принадлежащие одной цилиндрической соосной поверхности и нормалям, проведенным к ним из одной точки делительной поверхности (черт. 29)
Высота до постоянной хорды
Кратчайшее расстояние от вершины зуба эвольвентного цилиндрического зубчатого колеса до средней точки постоянной хорды (черт. 28)
Эквивалентное зубчатое колесо
Эвольвентное прямозубое цилиндрическое зубчатое колесо, размеры и форма зубьев которого в торцовом сечении приближенно совпадают с размерами и формой зуба эвольвентного косозубого цилиндрического зубчатого колеса в сечении его зуба плоскостью, нормальной к линии, равноудаленной от разноименных теоретических линий зуба и лежащей на одной с ними соосной цилиндрической поверхности.
Число зубьев эквивалентного колеса
7. Цилиндрические передачи Новикова
Косозубая цилиндрическая зубчатая передача с линейным контактом, у зубчатых колес которой выпуклые поверхности начальных головок зубьев взаимодействуют с вогнутыми поверхностями начальных ножек, и коэффициентом торцового перекрытия, равным нулю (или практически близким к нулю) (черт. 30)
Цилиндрическая передача Новикова
Косозубая цилиндрическая зубчатая передача с точечным (близким к линейному) контактом, номинальные поверхности зубьев зубчатых колес которой получены в результате профильной модификации сопряженных поверхностей зубьев зубчатых колес передачи Новикова с линейным контактом.
Цилиндрическая передача Новикова ОЛЗ
Цилиндрическая передача Новикова с точечным или близким к линейному контактом, имеющая одну линию зацепления (черт. 31)
Цилиндрическая передача Новикова ДЛЗ
Цилиндрическая передача Новикова с точечным (близким к линейному) контактом, имеющая две линии зацепления, каждая из которых образуется общей точкой контакта начальной ножки зуба одного зубчатого колеса с начальной головкой зуба парного зубчатого колеса (черт. 32 )
Интервал контактных точек зуба
Меньшее расстояние между двумя торцовыми сечениями сопряженных зубчатых колес передачи Новикова с двумя линиями зацепления, проведенными через контактные точки поверхности зуба зубчатого колеса (черт. 33).
Интервал контактных точек двух зубьев
Меньшее расстояние между двумя торцовыми сечениями сопряженных зубчатых колес передачи Новикова с двумя линиями зацепления, проведенными через контактные точки одноименных поверхностей двух соседних зубьев зубчатого колеса (черт. 33)
Номинальная толщина зуба, которая у зубчатого колеса цилиндрической передачи Новикова для обеспечения бокового зазора меньше, чем его теоретическая толщина зуба.
Правила построения терминов и определений видовых понятий цилиндрических зубчатых передач
Краткие формы терминов и обозначения в этих случаях совпадают.
Разрешается упомянутые термины, содержащиеся в ГОСТ 16530-83, применять непосредственно для понятий, относящихся к цилиндрическому зубчатому колесу и передаче, если обеспечивается однозначность их понимания.
Краткие формы терминов и обозначения остаются без изменения.
Обозначения соответствующих терминов совпадают. В кратких формах терминов слова «номинальная» и «зубчатая» опускаются.
Зубчатое колесо
Основу конструкции любого механизма составляют элементы, призванные передать механическое усилие от двигателя на рабочий орган. В зависимости от принципа действия принято различать несколько видов таких передач: клиноременные, фрикционные или червячные. Но самое широкое распространение в технике получили зубчатые передачи.
Такие механизмы в простейшем случае использующие сопрягаемую пару, включающую ведущую шестерню и колесо зубчатое. Благодаря зубчатой форме поверхности эти элементы входят в зацепление между собой и за счет этого передают вращение с одного вала на другой. Кроме возможности передать механическую мощность, такая передача способна обеспечить изменение скорости вращения выходного вала, относительно входного. Благодаря таким свойствам, практически в каждом промышленном механическом устройстве встречается редуктор, понижающий скорость вращения или мультипликатор, наоборот увеличивающий ее. В более сложных механизмах, так называемых коробках передач, группа зубчатых колес способна выполнить ступенчатое изменение скорости.
Широкое распространение зубчатые передачи получили благодаря высокой надежности и способности передавать момент в большом диапазоне нагрузок и скоростей вращения. При этом конструкция таких механизмов отличается относительной простотой и компактностью. Зубчатые передачи не предъявляют высоких требований к обслуживанию и характеризуются длительным сроком службы.
Наряду с очевидными достоинствами, этим механизмам присущ и ряд недостатков. В отличие от других типов передач, они более сложны в изготовлении, требуют более высокой точности обработки и применения специализированного обрабатывающего оборудования. Выбор материалов для зубчатых колес должен обеспечить сопротивляемость значительным механическим усилиям. Высокая жесткость, реализуемая зубчатой передачей, способствует минимизации потерь при передаче механической энергии. КПД таких механизмов приближаются к абсолютным значениям. Но при этом конструкция не позволяет преодолевать большие значения динамической нагрузки, что часто приводит к разрушению механизма. Еще одним негативным явлением, возникающим в процессе работы зубчатой пары, становится шум. Его уровень напрямую связан частотой вращения механизма и зависит от качества изготовления колес.
Виды зубчатых колес
Само название зубчатой передачи отражает ее конструкцию. В простейшем случае в состав такого механизма входят два вращающихся диска, на боковой поверхности, которых выполнены зубья. В процессе работы эти зубья зацепляются между собой. Колесо, связанное с источником вращающего момента, увлекает за собой второе. В итоге ведомый вал начинает вращаться.
В зависимости от направления передачи энергии используются разные обозначения зубчатых колес. Элемент, к которому присоединен вал двигателя, называется ведущим зубчатым колесом. В понижающих передачах оно характеризуется небольшим диаметром и малым числом зубьев. В технической литературе этот элемент часто называют шестерней. Сопрягаемое с ней колесо большого диаметра с большим числом зубьев называется ведомым. Вал этого колеса используется для передачи мощности на рабочий орган исполнительного механизма. Более сложные виды передач используют большее количество зубчатых колес. Например, такие устройства используются для реализации возможности отбора мощности от одного вала на несколько устройств или переключения скоростей вращения.
Высокие технические характеристики передачи и различные направления применения привели к созданию большого числа вариантов зубчатых колес. Наиболее простыми и распространенными из них являются цилиндрические прямозубые колеса. Зуб такой детали расположен на боковой поверхности колеса, параллельно оси. Второе колесо механической передачи имеет аналогичную геометрию. Оси обеих колес должны располагаться параллельно, на строго заданном расстоянии. Высокая технологичность изготовления этого типа деталей способствует массовому применению прямозубых передач в различных отраслях промышленности.
Из недостатков следует отметить только невысокий предельный момент. В сложных условиях работы используют другие виды зубчатых колес. Благодаря изменению геометрии зацепления, такие передачи обладают улучшенными свойствами. Например, для передач повышенной мощности проектируют косозубые колеса. В них ось зуба расположена под углом к оси вращения, за счет чего достигается большая зона контакта сопрягаемых деталей. В механизмах, характеризующихся сверхтяжелыми нагрузками, применяют шевронные модели. Зацепление в такой передаче выполняется на основе V-образных зубьев, чем обеспечивается оптимальное распределение нагрузки. Еще один вид зуба, называемый, круговым или криволинейным, выполняется в виде дуги. Он обеспечивает улучшенные механические характеристики, но достаточно трудоемок в изготовлении, поэтому большого распространения не получил.
Профиль или поперечное сечение зуба в механических передачах может быть практически любым. Встречаются варианты с треугольным, трапециевидным, прямоугольным или круглым профилем. Всем им, несмотря на простоту изготовления, свойственны недостатки, связанные с неравномерностью зацепления. Поэтому, в современных механических передачах, профиль чаще всего выполняется эвольвентным. Он представляет собой сложную кривую, обеспечивающую постоянное качество зацепления, вне зависимости от углового положения отдельных деталей и как следствие постоянство передаточного отношения. Такой профиль показывает оптимальные характеристики и относительно прост в изготовлении.
Кроме вида и профиля зуба, принято выделять и место его расположения. В зависимости от назначения, элементы зацепления могут быть расположены на внешней или внутренней части колеса. Также встречаются колеса с расположением зацепляющихся элементов со стороны торцевой части. Подобные шестерни называют корончатыми. Область их применения достаточно узка, поэтому встречаются они сравнительно редко. Гораздо более широкое применение получили передачи конического типа. Элементы зацепления в таких механизмах выполнены на поверхности усеченного конуса. Результирующее расположение конических шестерен подразумевает разное положение их осей в пространстве.
Еще один вид зубчатой передачи применяется в механизмах, преобразующих вращательное движение в возвратно-поступательное. Общее название таких устройств — рейка-шестерня.
Ведущий элемент такой передачи выполнен в виде обычного зубчатого колеса. Ведомая деталь представляет собой рейку, с нанесенными на одной из граней, зубьями. Вращение шестерни приводит к продольному перемещению рейки. Подобные передачи широко распространены в станочном оборудовании.
С зубчатыми колесами часто сравнивают звездочки цепных передач. Схожая форма деталей приводит к путанице. На самом деле цепная передача имеет иной принцип действия, а конструкция звездочки рассчитывается по собственным формулам.
Редкие модели
В общем случае считается, что зубчатое колесо должно иметь цилиндрическую форму. Но встречаются модели и некруглого типа. Главной их особенностью является переменное передаточное отношение, зависящее от угла поворота детали. Сегодня разработаны модели треугольной и квадратной формы, а также эллиптические шестерни. При постоянном вращении ведущего вала эти модели обеспечивают неравномерную скорость выходного. Высокая сложность изготовления и ограниченная область применения не дали подобным конструкциям широкого распространения. Тем не менее, сегодня встречаются отдельные устройства, в составе которых можно встретить некруглые шестерни. Примером могут служить редукторы некоторых насосов или специфические измерительные приборы.
Конструкция зубчатого колеса
Несмотря на кажущуюся простоту, в технике принято выделять несколько отдельных частей зубчатого колеса. Как и любое другое колесо, зубчатый вариант в своей основе имеет диск необходимого диаметра. Основной частью является обод, на боковой или торцевой поверхности которого выполнены зубья. Все вместе они образуют так называемый венец зубчатого колеса. Геометрия зубьев различна у разных типов зубчатой передачи. Сам зуб условно разбивается на несколько частей. Наружная часть называется вершиной. Прилегающие к ней боковые поверхности носят название головки зуба. Внутренняя часть именуется ножкой зуба. Две соседние ножки образуют впадину зубчатого колеса.
Для крепления на валу механизма в центре диска изготавливается ступица со сквозным отверстием. Форма отверстия зависит от геометрии сечения вала и может быть цилиндрической, квадратной или многоугольной. При использовании цилиндрических валов, в ступице обычно выполняют шпоночный паз.
С целью уменьшения веса толщина диска колеса выполняется обычно меньше, чем толщина ступицы или обода. Также для этого в теле диска могут присутствовать окна разнообразной формы.
Основные параметры
Для обеспечения подвижности и работоспособности, конструкция отдельных деталей механической передачи должна быть согласована по размерам и геометрии. Для этого при описании подобных устройств принято использовать систему специальных параметров. В их число входят геометрические, массогабаритные и прочностные величины, закрепленные стандартами. Применение стандартных параметров позволяет сравнительно просто производить расчет унифицированных зубчатых передач и обеспечивает гарантированное сопряжение всех изделий между собой. Естественно, что для разных видов, параметры будут несколько отличаться. Далее рассматриваются термины, связанные с конструкцией эвольвентного цилиндрического колеса. Эти параметры, в своем большинстве, описывают основные характеристики и других вариантов колес.
В основе сечения зуба большинства шестерен лежит эвольвентный профиль, который получается на основе одноименной кривой. Его применение легко стандартизируется, характеризуется высокой технологичностью изготовления и низкими требованиями к качеству сборки механизма. Основными параметры эвольвентного зубчатого колеса считаются модуль зацепления и количество зубьев зубчатого колеса. При одном и том же наружном диаметре деталей значения этих величин могут существенно отличаться в разных вариантах конструкции.
Число зубьев определяет коэффициент передачи и геометрические размеры зубьев. На ведущем колесе редуктора оно выполняется меньшим, чем на ведомом. В итоге один нормальный оборот ведущей шестерни приводит к повороту ведомого колеса только на определенный угол. Отношение числа зубьев двух колес дает значение передаточного коэффициента. Размеры зубьев определяются как отношение их количества к длине окружности колеса. С целью упрощения расчетов и гарантированного обеспечения зацепления между разными колесами, предусмотрен дополнительный параметр, называемый модулем зацепления. Любые шестерни с одинаковым модулем обеспечивают взаимодействие между собой и могут использоваться для построения механизмов, без дополнительной обработки.
Сумма ширины зуба и впадины совместно дают шаг зубчатого колеса. Учитывая неравномерность профиля по радиусу и зависимость длины дуги от диаметра, в каждом колесе можно определить бесконечное число значений этого параметра. С целью стандартизации принято рассматривать шаг по делительной окружности, называемый так же окружным шагом. Отношение этого шага к числу пи дает модуль зацепления. В некоторых случаях для описания шестерен используют угловой шаг, измеряемый в градусах. Стандартами предусмотрены и несколько других угловых величин. Например, для упрощения настройки оборудования при изготовлении колес рассматривают угловую ширину зуба и угловую ширину впадины. Определяются они также на основе делительной окружности.
Диаметры окружностей
Рассмотрение геометрии зубчатых пар невозможно без определения диаметров. На каждой детали их выделяется несколько. Широкое распространение имеет диаметр окружности по выступам, иногда называемый диаметром вершин. Он определяет максимальные габариты диска колеса. Его противоположностью считается диаметр окружности впадин. Разность этих величин, поделенная пополам, дает полную длину зуба. Но этот параметр в чистом виде не используется. При расчетах принято выделять высоту головки и ножки зуба. Граница, отделяющая два этих понятия, называется делительной окружностью зубчатого колеса. Диаметр данной окружности выполняет функцию опорного параметра при выполнении расчетов геометрии, так как именно по ней определяется окружной шаг и модуль зацепления. Еще один диаметральный параметр, называемый основной окружностью, описывает теоретическую кривую, которая является базой при построении эвольвенты. Диаметр основной окружности используется для построения конкретного профиля зуба.
Модуль зубчатого колеса
Универсальным понятием, позволяющим определить геометрические параметры деталей, выступает модуль зубчатой передачи. Его значение равно длине дуги в миллиметрах, приходящейся на один зуб колеса. Конкретное значение определяется по делительной окружности. Ее численно подбирают таким образом, что бы значение модуля совпадало с одним из общепринятых значений, найти которые можно в специальной литературе. В отечественной практике стандартные модули зубчатых колес нормированы в ГОСТ 9563-60. При проектировании шестерен обычно задаются значением этого параметра, а от него легко рассчитают все множество других. Исходными данными для определения требуемого модуля зубчатого колеса выступают расчеты прочности, призванные обеспечить требуемую мощность механической передачи.
Модуль зубчатого колеса связан с целым набором производных параметров. Используя несложные формулы расчета и значение необходимого числа зубьев, можно получить окружной шаг, диаметры верши и впадин, толщину зуба и ширину впадины по делительной окружности.
В зарубежной литературе аналогом отечественного модуля выступает питч. По своей сути это обратная к модулю зацепления величина, приведенная к дюймовой системе измерений. Аналогично для питчей разработаны специальные таблицы, содержащие нормированные значения параметра.
Расчет параметров
Расчет параметров зубчатых колес выполняют комплексно, для всей передачи. Необходимость расчета отдельного колеса возникает только в процессе ремонта оборудования с неизвестными данными. Расчет начинают с определения требуемого числа зубьев и модуля зацепления. Для того чтобы узнать значение модуля, предварительно проводят расчеты на прочность, исходя из срока службы и выбранного материала будущего механизма. Также на этом этапе рассчитывают межосевое расстояние между колесами. На основе полученных данных выносливости зубьев вычисляется минимально допустимая величина модуля зацепления. Конкретное его значение выбирается на основе таблиц, приведенных в справочной литературе. Далее, используя требуемое передаточное отношение, производится вычисление числа зубьев на сопрягаемых колесах.
При известном модуле зацепления и количестве зубьев шестерни и колеса, доступно произвести вычисление геометрических размеров отдельных деталей. Основные диаметры и профиль зуба передачи рассчитываются с использованием несложных арифметических действий. Сложные операции потребуются только для ограниченного числа параметров. Для цилиндрического прямозубого колеса тригонометрические функции содержат только формулы расчета делительного диаметра. При проектировании других типов зубчатых колес, используют тот же математический аппарат, что и для прямозубых, но с добавлением расчетов, учитывающих иную геометрию деталей. Результаты расчетов используют для построения чертежей будущих шестерен, а также при вычислении параметров редукторов.
Заключительным этапом расчета зубчатой передачи становится окончательная проверка механизма на прочность. Если результаты этих вычислений укладываются в принятые нормативы, то полученные значения величин можно использовать для изготовления готового механизма. В противном случае может потребоваться выполнить новый расчет, изменив исходные данные, например, увеличить геометрические размеры, либо поменять тип зубчатой передачи или количество ступеней редуктора.
Применение
Высокие свойства зубчатых передач нашли отражение в широком спектре применений. Во многих промышленных механизмах используются редукторы, призванные понизить число оборотов вращения вала двигателя, для передачи на технологическое оборудование. Помимо изменения скорости, такое устройство также увеличивает механический момент. В итоге маломощный двигатель с большой скоростью вращения, способен приводить в движение медленный и тяжелый механизм.
С целью уменьшения габаритов редуктора его часто выполняют многоступенчатым. Большое количество зубчатых колес входят в последовательное зацепление между собой, обеспечивая высокое передаточное число. Классическим примером подобного устройства являются обычные механические часы. Благодаря множеству специально подобранных передач, скорости движения секундной, минутной и часовой стрелок отличаются друг от друга ровно в 60 раз.
Зубчатые передачи позволяют реализовать и функцию регулирования скорости. Для этого применяются сменные комплекты колес, имеющих одинаковое межосевое расстояние и разное передаточное отношение.
Меняя один комплект на другой, можно получить разные скорости выходного вала. Этот принцип действия лег в основу коробок переключения передач, широко используемых в автомобилестроении, станкостроении и других отраслях.
Обычное зубчатое колесо допускает применение и для повышения скорости выходного вала относительно входного. В общем случае для этого достаточно развернуть редуктор или поменять местами точки подключения двигателя и конечного механизма. Называется подобное устройство мультипликатор. Из особенностей его применения необходимо учитывать запас по мощности двигателя, сопоставимый с передаточным числом механизма.
Зубчатые колеса используются также для изменения направления движения. Две цилиндрические шестерни с одинаковым числом зубьев реализуют функцию смены направления вращения вала. Передачи конической или корончатой конструкции используются в случае необходимости смены положения оси в пространстве. Ведущая и ведомая шестерни в таких механизмах развернуты друг относительно друга на какой-либо угол, значение которого может достигать 90 градусов. При этом передаточное отношение часто равно единице, что обеспечивает одинаковые скорости валов.
Наряду с простыми вариантами передач, содержащих зубчатые колеса, разработаны несколько специальных моделей. С целью снижения материалоемкости, в механизмах с ограниченным углом поворота, используют только часть зубчатого колеса. Такой сектор, обладая всеми основными свойствами зубчатого зацепления, отличается более низкой массой и стоимостью.
Еще один вариант, называемый планетарной передачей, также характеризуется малым весом и габаритами. При этом устройство обеспечивает высокое значение передаточного числа и пониженный уровень шума в процессе работы. Конструктивно такая передача состоит из нескольких шестерен, имеющих разную степень свободы. За счет этого механизм может не только передавать вращение, но и складывать или выделять угловые скорости разных валов, находящихся на одной оси. Сегодня разработано большое число вариантов планетарных передач, отличающихся типом и взаимным расположением зубчатых колес. Планетарные передачи широко применяются в автомобильной и авиационной технике, тяжелом металлорежущем оборудовании. Среди недостатков, сдерживающих распространение передач данного типа, следует отметить низкий КПД и высокие конструктивные требования к точности изготовления отдельных деталей.








