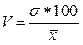Какие параметры являются мерами разброса распределений
Меры изменчивости (рассеивания, разброса)



Это статистические показатели, характеризующие различия между отдельными значениями выборки. Они позволяют судить о степени однородности полученного множества, о его компактности, а косвенно – и о надежности полученных данных и вытекающих из них результатов. Наиболее используемые в психологических исследованиях показатели: размах, среднее отклонение, дисперсия, стандартное отклонение, полуквартильное отклонение. Размах (Р) – это интервал между максимальным и минимальным значениями признака. Определяется легко и быстро, но чувствителен к случайностям, особенно при малом числе данных.
Примеры: 0, 2, 3, 5, 8 (Р = 8-0 = 8);
-0.2, 1.0, 1.4, 2.0 (Р = 2,0-(-0,2) = 2,2);0,2,3,5,67 (Р = 67-0 = 67).
Среднее отклонение (МД) – это среднеарифметическое разницы (по абсолютной величине) между каждым значением в выборке и ее средним:
где d = |Х– M|; М – среднее выборки; X – конкретное значение; N – число значений.
Множество всех конкретных отклонений от среднего характеризует изменчивость данных, но если их не взять по абсолютной величине, то их сумма будет равна нулю. И вся информация пропадает. МД показывает степень скученности данных вокруг среднего. Кстати, иногда при определении этой характеристики выборки вместо среднего (М) берут иные меры центральной тенденции – моду или медиану.
Дисперсия (Д) (от лат. dispersus – рассыпанный). Другой путь измерения степени скученности данных – это избегание нулевой суммы конкретных разниц (d = Х-М) не через их абсолютные величины, а через их возведение в квадрат, и тогда получают дисперсию:
Д = ∑d 2 / N – для больших выборок (N > 30); Д = ∑d 2 / (N-1) – для малых выборок (N
Понятно, что при симметричном распределении точка Q2 совпадет с медианой (а следовательно, и со средним), и тогда можно вычислить коэффициент Q для характеристики разброса данных относительно середины распределения. При несимметричном распределении этого недостаточно. И тогда дополнительно вычисляют еще два коэффициента Q – для правого и левого участков:
Какие параметры являются мерами разброса распределений
Войти
Авторизуясь в LiveJournal с помощью стороннего сервиса вы принимаете условия Пользовательского соглашения LiveJournal
5. Описательные статистики: Меры разброса.
Дисперсия и среднеквадратичное отклонение: формула и интерпретация.
Из математической статистики известно, что самой известной мерой разброса количественного признака является его дисперсия:
(напомним, что в знаменателе величина объема выборки уменьшается на единицу для того, чтобы сделать соответствующую точечную выборочную оценку дисперсии несмещенной; – среднее квадратическое отклонение). Стандартное отклонение – на сколько в среднем отклонение значения от среднего значения величины.
Квантильный размах: подсчет и интерпретация.
Представляется, что прежде, чем переходить к описанию мер разброса для номинальных признаков, необходимо пояснить, каков “физический” смысл таких мер.
Так же используется Range – разность между максимальным и минимальным значением.
Для каких типов шкал возможно вычисление искомых статистик.
Дисперсия может быть подсчитана только для метрических шкал. Межквартильный размах считаю для номинальных
Ассиметрия и эксцесс: понятие, смысл, особенности использования.
Skewness – это ассиметрия (скошенность). Если в результате отношения статистики к ее стандартной ошибке получается большое положительное значение, то это значит, что график распределения имеет длинный «хвост» справа. Если в результате отношения статистики к ее стандартной ошибке получается большое отрицательное значение, то это значит, что график распределения имеет длинный «хвост» слева.
Kurtosis – это эксцесс (пикообразность). Коэффициент эксцесса нормального распределения равен нулю. Он положителен, если пик распределения около математического ожидания острый, и отрицателен, если пик гладкий.
Распределение переменной «возраст» не является нормальным, т.к. отношения ассиметрии и эксцесса к их стандартным ошибкам не попадает в интервал [-2; 2]. Кроме того график распределения данной переменной имеет длинный “хвост” справа.
Мера разброса относительно среднего положения распределения.
Одна из самых важных характеристик распределения – это мера разброса отдельных значений относительно среднего. Известны восемь различных мер этой характеристики, четыре из них широко используются в геологических прикладных науках.
1. Первая мера разброса значений относительно среднего – это размах распределения R:
2. Вторая мера это дисперсия. Дисперсия – это среднее значение квадратов отклонений всех возможных значений случайной величины от истинного среднего совокупности μ:
S 2 =1/n-1 *[∑ xi 2 –1/n(∑ χ) 2 ], или
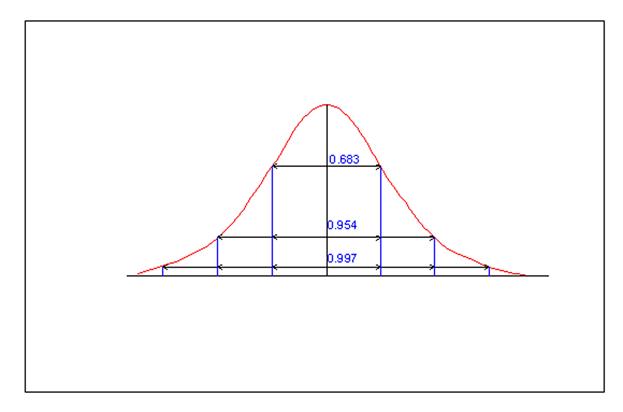
Рис. Площади стандартного нормального распределения, заключенные в пределах интервалов, кратных стандартному отклонению.
4. Четвертая мера – это коэффициент вариации. Его часто используют при разведке и оценке месторождений полезных ископаемых. Коэффициент вариации определяется как отношение стандартного отклонения на выборочное среднее и умноженное на 100%. Важным свойством коэффициента вариации является его безразмерность, поэтому он так широко и используется в различных методических руководствах, регламентирующих проведение геологоразведочных работ:
Остальные меры разброса значений относительно среднего, такие как коэффициент осцилляции, среднее линейное отклонение, относительное линейное отклонение и геометрическая дисперсия используются реже.
VR= (R/χ)*100, где R = max – min.
6. Шестая мера – среднее линейное отклонение, рассчитывается по формуле:
7. Седьмая мера – это относительное линейное отклонение, рассчитывается по формуле:
8. Восьмая мера – геометрическая дисперсия. Она рассчитывается по следующей формуле:
Практическое значение геометрической дисперсии станет ясным при рассмотрении асимметричных распределений.
Частотное распределение и его параметры. Основные меры центральной тенденции и разброса
Распределением называется закономерность встречаемости признака и разных его значений. Статистическое распределение может иметь графическое представление в виде полигона частот (ломаной линии, соединяющей точки, соответствующие величинам частот, откладываемым по оси ординат). Форма распределения является некоторой обобщенной характеристикой выборки. Кривые распределения бывают одновершинные и многовершинные. В психологических исследованиях чаще всего ссылаются на нормальное распределение.
Нормальное распределение – вид распределения переменных, характеризуемое тем, что крайние значения признака в нем ссылаются достаточно редко, а значения, близкие к средней величине – достаточно часто. Нормальным такое распределение называется потому, что оно очень часто встречалось в естественно-научных исследованиях и казалось “нормой” всякого массового проявления признаков. Это распределение следует закону, открытому в разное время: Муавром в 1733 г. в Англии, Гауссом в 1809 г. в Германии и Лапласом в 1812 г. во Франции. График нормального распределения представляет симметричную унимодальную колоколообразную кривую (верхняя часть колокола), осью которой является вертикаль (ордината), проведенная через точку 0.
Рисунок 1. Процентное распределение случаев под нормальной кривой
Для любого нормального распределения в пределах М + 1s лежит около 68%, в пределах
М + 2s – 95%, М + 3s – 99,7% (М – среднее арифметическое).
Параметры распределения – это его числовые характеристики, указывающие, где в “среднем” располагаются значения признака, насколько эти значения изменчивы и наблюдается ли преимущественное появление определенных значений признака. Характеристики совокупности переменных (признаков), указывающие на наиболее типичный, репрезентативный для изучаемой выборки результат называются мерами центральной тенденции.Наиболее практически важными мерами центральной тенденции являются математическое ожидание (или среднее арифметическое), мода, медиана.
а) Среднее арифметическое (М – оценка математического ожидания) – это обобщающий показатель положения уровня центра распределения. Оно вычисляется по формуле:
где хi – каждое наблюдаемое значение признака;
i – индекс, указывающий на порядковый номер данного значения признака;
n – количество наблюдений;
S – знак суммирования.
б) Медиана (Ме) – центральное значение переменной: результат, находящийся в середине последовательности показателей, если их расположить в порядке возрастания или убывания.
в) Мода (Мо) – наиболее часто встречающийся результат (самая высокая точка кривой распределения).
При выборе и интерпретации мер центральной тенденции необходимо учитывать следующие особенности и правила использования приведенных показателей.
1. При определении средних величин необходимо тщательное соблюдение требований однородности переменных, репрезентативности и достаточности объема выборки.
2. Расчету средних величин должна предшествовать предварительная разбивка изучаемой совокупности на качественно однородные группы.
3. Медиана не зависит от величин и частот встречаемости в рамках определенного множества переменных.
4. В малых совокупностях мода нестабильна и может сильно изменяться при единичных и незначительных вариациях переменных.
5. Каждое значение переменной влияет на величину средних. Если одно какое-нибудь значение меняется на С единиц, среднее арифметическое меняется в том же направлении на 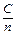
6. В унимодальных симметричных выборках среднее, медиана и мода совпадают.
7. Являясь обобщенной характеристикой ряда, меры центральной тенденции не позволяют учитывать его вариации. Наряду с мерами центральной тенденции обязательно использование мер изменчивости.
Различные меры изменчивости распределения характеризуют степень и характер вариации признаков.
Меры изменчивости– статистические показатели вариации (разброса) признака (переменной) относительно среднего значения, степени индивидуальных отклонений от центральной тенденции распределения. Меры изменчивости позволяют судить о достоверности и однородности полученной эмпирически совокупности данных, существенности сходств и различий в распределении и сравниваемых группах распределений, точности проведенных измерений. Среди прочих показателей к ним относятся: размах распределения, дисперсия, стандартное отклонение, показатели асимметрии и эксцесса.
Размах распределения – разность между самым высоким и самым низким результатом.
Дисперсия(S, s2) характеризует средний разброс значений по выборке относительно среднего арифметического, возведенный в квадрат. Расчет дисперсии применяют для выделения выборочной совокупности, определения ошибки выборки, однородности изучаемой совокупности по тому или иному признаку.
На практике, однако, чаще используют другой показатель – стандартное отклонение
(s или sх) – показатель, представляющий собой квадратный корень из несмещенной оценки дисперсии.
Дисперсия и стандартное отклонение (или среднее квадратичное отклонение) имеют некоторые недостатки. Они недостаточно точно характеризуют изменчивость признака, т.к. отражают абсолютный размер отклонений. Это неудобно при сопоставлении распределений с различной размерностью и значением признаков. Для устранения этого недостатка абсолютные числа переводятся в относительные. Отношение стандартного отклонения к средней, выраженное в процентах, называется коэффициентом вариации V:
В тех случаях, когда какие-нибудь причины благоприятствуют более частому появлению значений, которые выше или, наоборот, ниже среднего, образуются асимметричные распределения. Показатель асимметрии (А) может быть положительным или отрицательным. При левосторонней, или положительной асимметрии в распределении чаще встречаются более низкие значения признака, а при правосторонней, или отрицательной – более высокие.
В тех случаях, когда какие-нибудь причины способствуют преимущественному появлению средних или близких к средним значений, образуется распределение с положительным эксцессом(Е).
Если же в распределении преобладают крайние значения, причем одновременно и более низкие, и более высокие, то такое распределение характеризуется отрицательным эксцессом и в центре распределения может образоваться впадина, превращающая его в двухвершинное. В нормальных распределениях асимметрия равна нулю, эксцесс – трем.
Урок на тему “Меры разброса”
Новые аудиокурсы повышения квалификации для педагогов
Слушайте учебный материал в удобное для Вас время в любом месте
откроется в новом окне
Выдаем Удостоверение установленного образца:
Основные определения: Размах;Отклонение от среднего;Дисперсия;Среднее квадратичное отклонение;
Например в выборке : 80;89;320;4600; наибольшее число 4600, наименьшее 80. Следовательно, размах ( R )=4600-80 = 4520.
Отклонением от среднего называют разность между рассматриваемым значением случайной величины и средним значением выборки.
Отклонение от среднего может быть как положительным, так и отрицательным числом. Характеристикой стабильности элементов совокупности может служить сумма квадратов отклонений от среднего (чем меньше, тем лучше).
Среднее арифметическое квадратов отклонений называется дисперсией ( D ).
Корень квадратный из дисперсии называют средним квадратичным отклонением и обозначают σ= .
Найти размах выборки:
Найти дисперсию выборки:
Найти дисперсию совокупности значений случайной величины X , заданной частотным распределением:
Найти среднее квадратичное отклонение от среднего значения элементов выборки:
Сравнить дисерсии двух выборок, имеющих одинаковые квадратичные отклонения:
6, 10, 7, 8, 9 и 8, 9, 5, 10;
5, 12, 7, 8, 18 и 17, 6, 3 11, 7, 9, 10;
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
Номер материала: ДБ-1287663
Не нашли то что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
ЕГЭ в 2022 году может пройти в допандемийном формате
Время чтения: 1 минута
Минобрнауки предлагает дифференцированный подход к аккредитации вузов
Время чтения: 1 минута
Школы организуют экскурсии и спортивные игры в день выборов
Время чтения: 1 минута
Половина российских студентов отдают предпочтение гибридному формату обучения
Время чтения: 1 минута
Учитель математики из Казани вышел в финал Международной премии для учителей
Время чтения: 1 минута
В пяти регионах России протестируют новую систему оплаты труда педагогов
Время чтения: 2 минуты
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.