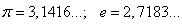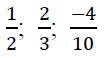какие виды чисел бывают в математике

Математика

Тестирование онлайн

Натуральные числа

Это числа, которые используются при счете: 1, 2, 3. и т.д.

Ноль не является натуральным.

Натуральные числа принято обозначать символом N.

Целые числа. Положительные и отрицательные числа

Натуральные числа, противоположные им и ноль называют целыми числами. Множество целых чисел обозначают символом Z.

Рациональные числа

Множество рациональных чисел обозначается Q. Все целые числа являются рациональными.

Иррациональные числа

Бесконечная непериодическая дробь называется иррациональным числом. Например:

Множество иррациональных чисел обозначается J.

Действительные числа

Множество всех рациональных и всех иррациональных чисел называется множеством действительных (вещественных) чисел.

Действительные числа обозначаются символом R.

Округление чисел

Округлить 8,759123. с точностью до целой части.

Округлить 8,759123. с точностью до десятой части.

Округлить 8,759123. с точностью до сотой части.

Округлить 8,759123. с точностью до тысячной части.

Источник

Числа: натуральные, целые, рациональные, иррациональные, действительные

Натуральные числа

Натуральные числа определение – это целые положительные числа. Натуральные числа используют для счета предметов и многих иных целей. Вот эти числа:

Это натуральный ряд чисел.
Ноль натуральное число? Нет, ноль не является натуральным числом.
Сколько натуральных чисел существует? Существует бесконечное множество натуральных чисел.
Каково наименьшее натуральное число? Единица — это наименьшее натуральное число.
Каково наибольшее натуральное число? Его невозможно указать, ведь существует бесконечное множество натуральных чисел.

Сумма натуральных чисел есть натуральное число. Итак, сложение натуральных чисел a и b:

с — это всегда натуральное число.

Произведение натуральных чисел есть натуральное число. Итак, произведение натуральных чисел a и b:

с — это всегда натуральное число.

Разность натуральных чисел Не всегда есть натуральное число. Если уменьшаемое больше вычитаемого, то разность натуральных чисел есть натуральное число, иначе — нет.

Частное натуральных чисел Не всегда есть натуральное число. Если для натуральных чисел a и b

где с — натуральное число, то это значит, что a делится на b нацело. В этом примере a — делимое, b — делитель, c — частное.

Делитель натурального числа — это натуральное число, на которое первое число делится нацело.

Каждое натуральное число делится на единицу и на себя.

Простые натуральные числа делятся только на единицу и на себя. Здесь имеется ввиду делятся нацело. Пример, числа 2; 3; 5; 7 делятся только на единицу и на себя. Это простые натуральные числа.

Единицу не считают простым числом.

Числа, которые больше единицы и которые не являются простыми, называют составными. Примеры составных чисел:

Единицу не считают составным числом.

Множество натуральных чисел составляют единица, простые числа и составные числа.

Множество натуральных чисел обозначается латинской буквой N.

Свойства сложения и умножения натуральных чисел:

переместительное свойство сложения

сочетательное свойство сложения

переместительное свойство умножения

сочетательное свойство умножения

распределительное свойство умножения

Целые числа

Целые числа — это натуральные числа, ноль и числа, противоположные натуральным.

Числа, противоположные натуральным — это целые отрицательные числа, например:

Множество целых чисел обозначается латинской буквой Z.

Рациональные числа

Рациональные числа — это целые числа и дроби.

Любое рациональное число может быть представлено в виде периодической дроби. Примеры:

Из примеров видно, что любое целое число есть периодическая дробь с периодом ноль.

Любое рациональное число может быть представлено в виде дроби m/n, где m целое число,n натуральное число. Представим в виде такой дроби число 3,(6) из предыдущего примера:

Другой пример: рациональное число 9 может быть представлено в виде простой дроби как 18/2 или как 36/4.

Множество рациональных чисел обозначается латинской буквой Q.

Подробнее о рациональных числах в разделе Рациональные числа.

Иррациональные числа

Иррациональные числа — это бесконечные непериодические десятичные дроби. Примеры:

Подробнее об иррациональных числах в разделе Иррациональные числа.

Действительные числа

Действительные числа – это все рациональные и все иррациональные числа.

Множество действительных чисел обозначается латинской буквой R.

Источник

Виды чисел.

У нас есть числа натуральные, целые, рациональные и иррациональные, а также вещественные или действительные и еще есть другие, но в школьной программе в основном используют эти числа.

Натуральные числа ( N ) − это числа, используемые для счета предметов. Нуль не является натуральным числом.
Например: 1; 2; 3; 132; 168; 326; 548; 10050…

Целые числа ( Z ) — множество чисел, получающееся в результате арифметических операций сложения (+) и вычитания (−) натуральных чисел.
Например: …−3; −2; 1; 0; 548; 10050…

Рациональные числа ( Q ) – это положительные и отрицательные числа можно представить в виде обыкновенной несократимой дроби вида: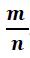

где m−целое число (числитель), n – натуральное число (знаменатель).
Например:

Иррациональные числа ( I ) − числа, которые не представимыми в виде дроби вида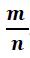

Например: √2; √5; π; e

Вещественные (действительные) числа ( R ).
Рациональные числа и иррациональные числа образуют множество действительных чисел.
Изобразим это множество чисел в виде рисунка:

Видно их вложенность друг в друга.

Подписывайтесь на канал на YOUTUBE и смотрите видео, подготавливайтесь к экзаменам по математике и геометрии с нами.

Источник

Алгебра

План урока:

Натуральные числа

Ещё в далекие доисторические времена человек освоил такую математическую операцию, как счет. Можно было подсчитать количество соплеменников в племени или животных в стае, на которых велась охота. При этом человек ещё не осознавал понятие числа как некое отвлеченное понятие. Анализ языков народов, находящихся на самых низких стадиях развития, показывает, что они в словосочетаниях «три змеи», «три палки», «три камня» используют разные слова для числа 3. Однако со временем человек осознал, что количество предметов можно определять числом, которое не будет зависеть от природы подсчитываемых объектов. Числа, используемые для счета, сегодня называют натуральными числами. Долгое время человечество не знало никаких других чисел.

В качестве примера можно привести следующие натуральные числа: 1, 8, 10, 1000, 64141 и т.п. Если можно представить, что в каком-то множестве содержится N элементов, то N будет натуральным числом.

Вообще все натуральные числа являются частью так называемого натурального ряда чисел. Начинается этот ряд с единицы, а каждое следующее число больше предыдущего на 1.

Таким образом, можно дать ещё одно определение натуральных чисел – это числа, входящие в натуральный ряд. Традиционно ноль не является натуральным числом, ведь при подсчете предметов счет начинают с единицы. Такой подход используется в большинстве российских источников. Однако стоит отметить, что иногда в зарубежной литературе всё же предпочитают начинать натуральный ряд не с единицы, а с нуля. В этом случае 0 становится натуральным числом. Это деление весьма условно. Для обозначения множества натуральных чисел используется буква N. Очевидно, что натуральных чисел существует бесконечно много, а потому не существует наибольшего натурального числа.

Любые два натуральных числа можно складывать друг с другом и перемножать, при этом в результате будет снова получаться натуральное число. При вычитании может получиться ноль или отрицательное число, а при делении – дробное.

Простые и составные числа

Все натуральные числа можно разбить на три группы:

Единицу традиционно не считают ни простым, ни составным числом. Составным же называют натуральное число, делящееся не только на единицу и себя. Можно дать и другие определения, основанные на количестве делителей у числа. Так, единица имеет ровно 1 делитель. У простого числа всегда ровно 2 делителя, а у составного – 3 и более.

В качестве примера простых чисел можно привести: 2, 3, 5, 7, 31, 101, 163. Примерами составных чисел являются:

Среди делителей составного числа могут быть как другие составные, так и простые числа. Например, 50 имеет простые делители 2 и 5 и составные 10 и 25.

Заметим, что если число n делится на m, а m в свою очередь делится на k, то и n делится на k. Так, 45 делится на 9, а 9 делится на 3. Значит, и 45 делится на 3. Из этого свойства чисел вытекает следующее утверждение:

Любое составное число имеет хотя бы один простой делитель, причем им обязательно будет наименьший из всех делителей числа. Докажем это. Пусть число H – составное, и имеет наименьший делитель F. Предположим, что F – составное число. Тогда у него есть делитель L, который меньше его. Но тогда L должен быть делителем и для H. Так как L 1 1

Источник

Понятие числа. Виды чисел.

Число — абстракция, используемая для количественной характеристики объектов. Числа возникли еще в первобытном обществе в связи с потребностью людей считать предметы. С течением времени по мере развития науки число превратилось в важнейшее математическое понятие.

Для решения задач и доказательства различных теорем необходимо понимать, какие бывают виды чисел. Основные виды чисел включают в себя: натуральные числа, целые числа, рациональные числа, действительные числа.

Натуральные числа – это числа, получаемые при естественном счёте предметов, а вернее при их нумерации («первый», «второй», «третий». ). Множество натуральных чисел обозначается латинской буквой N (можно запомнить, опираясь на английское слово natural). Можно сказать, что N =

Рациональные числа – это числа, представимые в виде дроби, где m — целое число, а n — натуральное число. Для обозначения рациональных чисел используется латинская буква Q. Все натуральные и целые числа – рациональные.

Действительные (вещественные) числа – это числа, которое применяются для измерения непрерывных величин. Множество действительных чисел обозначается латинской буквой R. Действительные числа включают в себя рациональные числа и иррациональные числа. Иррациональные числа – это числа, которые получаются в результате выполнения различных операций с рациональными числами (например, извлечение корня, вычисление логарифмов), но при этом не являются рациональными.

1. Системы счисления.

Система счисления – способ наименования и записи чисел. В зависимости от способа изображения чисел разделяется на позиционные-десятичная и непозиционные-римская.

В ПК используют 2ичную, 8ричную и 16ричную системы счисления.

Отличия:запись числа в 16ной системе счисленич по сравнению с другой записью значительно короче, т.е. требует меньшего количества разрядности.

В позиционной системе счисления каждая цифра сохраняет свое постоянное значение независимо от занимаемой позиции в числе. В позиционной системе счисления каждая цифра определяет не только свое значение, но зависит от того положения, которое она занимает в числе. Каждая система счисления характеризуется основанием. Основание- это количество различных цифр, которые используются для записи чисел в данной системе счисления. Основание показывает во сколько раз изменяется значение одной и той же цифры при переходе на соседнюю позицию. В компьютере используется 2-система счисления. Основанием системы может быть любое число. Арифметические дей-ия над числами в любой позиции выполняются по правилам аналогичным 10 системе счисления. Для 2 системы счисления используется двоичная арифметика, которая реализуется в компьютере для выполнения арифметических вычислений.

Сложение двоичных чисел:0+0=1;0+1=1;1+0=1;1+1=10

В компьютере широко применяется 8 система счисления и 16 система счисления. Они используются для сокращения записи двоичных чисел

2. Понятие множества.

Понятие «множество» является фундаментальным понятием математики и не имеет определения. Природа порождения любого множества разнообразна, в частности, окружающие предметы, живая природа и др.

Определение 1: Объекты, из которых образовано множество, называются элементами данного множества. Для обозначения множества используют заглавные буквы латинского алфавита: например X, Y, Z, а в фигурных скобках через запятую выписывают его элементы строчными буквами, например: .

Пример обозначения множества и его элементов:

X = 1, x₂,…, x_n> – множество, состоящее из n элементов. Если элемент x принадлежит множеству X, то следует записать: xÎX, иначе элемент x не принадлежит множеству X, что записывается: xÏX. Элементами абстрактного множества могут быть, например, числа, функции, буквы, фигуры и т.д. В математике в любом разделе используется понятие множества. В частности, можно привести некоторые конкретные множества вещественных чисел. Множество вещественных чисел х, удовлетворяющих неравенствам:

· а ≤ x ≤ b называется сегментом и обозначается [a,b];

Простые высказывания, входящие в составные, сами по себе могут быть совершенно произвольными. В частности, они сами могут быть составными. Описываемые ниже базисные типы составных высказываний определяются независимо от образующих их простых высказываний.

11. Операции над высказываниями.

1.Операция отрицания.

Отрицанием высказывания Аназывается высказывание, обозначаемое (читается «не А», «неверно, что А»), которое истинно, когда А ложно и ложно, когда А – истинно.

Отрицающие друг друга высказывания А и называются противоположными.

2. Операция конъюнкции.

Конъюнкцией высказываний А и В называется высказывание, обозначаемое А 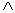В (читается «А и В»), истинные значения которого определяются в том и только том случае, когда оба высказывания А и В истинны.

Конъюнкцию высказываний называют логическим произведением и часто обозначают АВ.

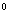
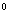
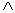
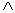
Пусть дано высказывание А – «в марте температура воздуха от 0 С до +7 С» и высказывание В – «в Витебске идет дождь». Тогда А В будет следующей: «в марте температура воздуха от 0 С до +7 С и в Витебске идет дождь». Данная конъюнкция будет истинной, если будут высказывания А и В истинными. Если же окажется, что температура была меньше 0 С или в Витебске не было дождя, то А В будет ложной.

3. Операция дизъюнкции.

Дизъюнкцией высказываний А и В называется высказывание А 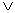В (А или В), которое истинно тогда и только тогда, когда хотя бы одно из высказываний истинно и ложно – когда оба высказывания ложны.

Дизъюнкцию высказываний называют также логической суммой А+В.

Дата добавления: 2017-04-20 ; просмотров: 12902 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник