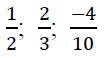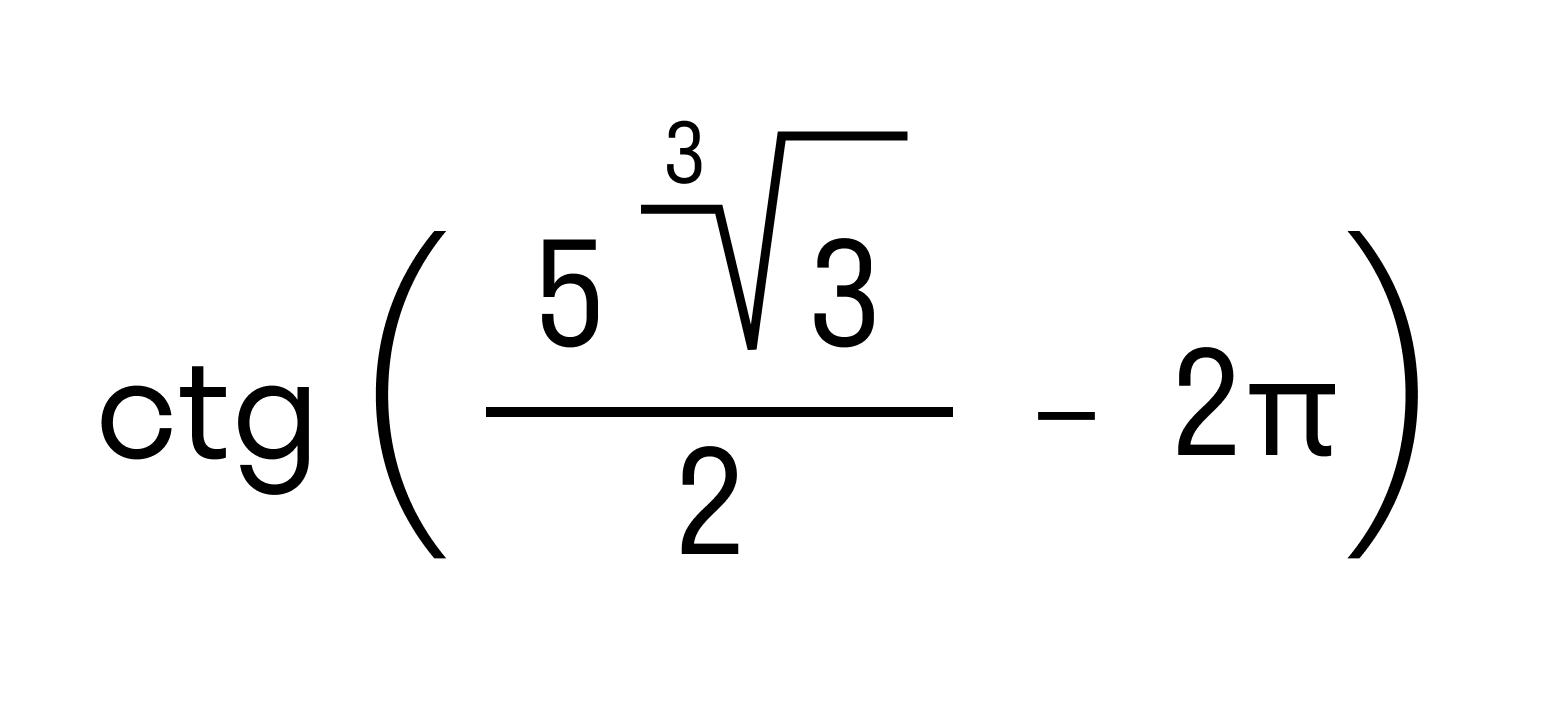какие виды чисел существуют
Виды чисел.
У нас есть числа натуральные, целые, рациональные и иррациональные, а также вещественные или действительные и еще есть другие, но в школьной программе в основном используют эти числа.
Натуральные числа ( N ) − это числа, используемые для счета предметов. Нуль не является натуральным числом.
Например: 1; 2; 3; 132; 168; 326; 548; 10050…
Целые числа ( Z ) — множество чисел, получающееся в результате арифметических операций сложения (+) и вычитания (−) натуральных чисел.
Например: …−3; −2; 1; 0; 548; 10050…
Рациональные числа ( Q ) – это положительные и отрицательные числа можно представить в виде обыкновенной несократимой дроби вида: 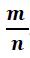
где m−целое число (числитель), n – натуральное число (знаменатель).
Например:
Иррациональные числа ( I ) − числа, которые не представимыми в виде дроби вида 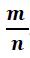
Например: √2; √5; π; e
Вещественные (действительные) числа ( R ).
Рациональные числа и иррациональные числа образуют множество действительных чисел.
Изобразим это множество чисел в виде рисунка:
Видно их вложенность друг в друга.
Подписывайтесь на канал на YOUTUBE и смотрите видео, подготавливайтесь к экзаменам по математике и геометрии с нами.
Сообщение по алгебре на тему “Виды чисел”
Сообщение по математике
Холодные числа, внешне сухие формулы математики полны внутренней красоты и жара сконцентрированной в них мысли
Учитель математики: Амирокова Ф.М
Целые и рациональные числа
Со сложением всё понятно: сложив любые два натуральных числа, в результате всегда получим тоже натуральное число. А вот в вычитании обнаруживаем, что из меньшего отнять большее так, чтобы в результате получилось натуральное число, мы не можем. (3 − 5 = чему?) Здесь возникает идея отрицательных чисел. (Отрицательные числа уже не являются натуральными)
На этапе возникновения отрицательных чисел (а они появились позже дробных)существовали и их противники, считавшие их бессмыслицей. (Три предмета можно показать на пальцах, десять можно показать, тысячу предметов можно представить по аналогии. А что такое “минус три мешка”? — В то время числа хоть уже и использовались сами по себе, в отрыве от конкретных предметов, количество которых они обозначают, всё ещё были в сознании людей гораздо ближе к этим конкретным предметам, чем сегодня.) Но, как и возражения, так и основной аргумент в пользу отрицательных чисел, пришел из практики: отрицательные числа позволяли удобно вести счет долгам. 3 − 5 = −2 — у меня было 3 монеты, я потратила 5. Значит, у меня не просто закончились монеты, но и 2 монеты я кому-то должна. Если верну одну, долг изменится −2+1=−1, но тоже может быть представлен отрицательным числом.
Определение: Натуральные числа, им противоположные и нуль составляют множество целых чисел. Оно обозначается буквой Z.
Любые два целых числа можно вычесть друг из друга или сложить и получить в результате целое число.
Идея сложения целых чисел уже предполагает возможность умножения, как просто более быстрого способа выполнения сложения. Если у нас есть 7 мешков по 6 килограмм, мы можем складывать 6+6+6+6+6+6+6 (семь раз прибавлять к текущей сумме по 6), а можем просто помнить, что такая операция всегда будет давать в результате 42. Как и сложение шести семерок 7+7+7+7+7+7 тоже всегда будет давать 42.
Результаты операции сложения определенного числа самого с собой определенное количество раз для всех пар чисел от 2 до 9 выписываются и составляют таблицу умножения. Для умножения целых чисел больше 9 придумывается правило умножения в столбик. (Которое распространяется и на десятичные дроби, и которое будет рассматриваться в одной из следующих статей.) При умножении любых двух целых чисел друг на друга всегда получим в результате целое число.
Введение рациональных чисел, то есть чисел вида m/n, где m – целое число, n – натуральное число, позволило находить частное любых двух чисел при условии, что делитель не равен нулю. Каждое целое число m также является рациональным, так как его можно представить в виде m/1.
! Периодическая дробь – это бесконечная десятичная дробь, у которой, начиная с некоторого десятичного знака, повторяется одна и та же цифра или группа цифр – период дроби.
! Каждое рациональное число можно представить в виде бесконечной периодической десятичной дроби
Натуральные числа
Определение натурального числа
Натуральные числа — это числа, которые мы используем для подсчета чего-то конкретного, осязаемого.
Вот какие числа называют натуральными: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, …
Натуральный ряд — последовательность всех натуральных чисел, расположенных в порядке возрастания. Первые сто можно посмотреть в таблице.
Какие операции возможны над натуральными числами
Записывайтесь на курсы по математике для учеников с 1 по 11 классы!
Десятичная запись натурального числа
В школе мы проходим тему натуральных чисел в 5 классе, но на самом деле многое нам может быть интуитивно понятно и раньше. Проговорим важные правила.
Мы регулярно используем цифры: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. При записи любого натурального числа можно использовать только эти цифры без каких-либо других символов. Записываем цифры одну за другой в строчку слева направо, используем одну высоту.
Примеры правильной записи натуральных чисел: 208, 567, 24, 1 467, 899 112. Эти примеры показывают нам, что последовательность цифр может быть разной и некоторые даже могут повторяться.
077, 0, 004, 0931 — это неправильные примеры натуральных чисел, потому что ноль расположен слева. По правилам так нельзя. Это и есть десятичная запись натурального числа.
Количественный смысл натуральных чисел
Натуральные числа несут в себе количественный смысл, то есть выступают в качестве инструмента для нумерации.
Представим, что перед нами банан 🍌. Мы можем записать, что видим 1 банан. При этом натуральное число 1 читается как «один» или «единица».
Но термин «единица» имеет еще одно значение: то, что можно рассмотреть, как единое целое. Элемент множества можно обозначить единицей. Например, любое дерево из множества деревьев — единица, любой листок из множества листков — единица.
Представим, что перед нами 2 банана 🍌🍌. Натуральное число 2 читается как «два». Далее, по аналогии:
| 🍌🍌🍌 | 3 предмета («три») |
| 🍌🍌🍌🍌 | 4 предмета («четыре») |
| 🍌🍌🍌🍌🍌 | 5 предметов («пять») |
| 🍌🍌🍌🍌🍌🍌 | 6 предметов («шесть») |
| 🍌🍌🍌🍌🍌🍌🍌 | 7 предметов («семь») |
| 🍌🍌🍌🍌🍌🍌🍌🍌 | 8 предметов («восемь») |
| 🍌🍌🍌🍌🍌🍌🍌🍌🍌 | 9 предметов («девять») |
Основная функция натурального числа — указать количество предметов.
Если запись числа совпадает с цифрой 0, то его называют «ноль». Напомним, что ноль — не натуральное число, но он может обозначать отсутствие. Ноль предметов значит — ни одного.
Однозначные, двузначные и трехзначные натуральные числа
Однозначное натуральное число — это такое число, в составе которого один знак, одна цифра. Девять однозначных натуральных чисел: 1, 2, 3, 4, 5, 6, 7, 8, 9.
Двузначные натуральные числа — те, в составе которых два знака, две цифры. Цифры могут повторяться или быть различными. Например: 88, 53, 70.
Если множество предметов состоит из девяти и еще одного, значит, речь идет об 1 десятке («один десяток») предметов. Если один десяток и еще один, значит, перед нами 2 десятка («два десятка») и так далее.
По сути, двузначное число — это набор однозначных чисел, где одно записывается справа, а другое слева. Число слева показывает количество десятков в составе натурального числа, а число справа — количество единиц. Всего двузначных натуральных чисел — 90.
Трехзначные натуральные числа — числа, в составе которых три знака, три цифры. Например: 666, 389, 702.
Одна сотня — это множество, состоящее из десяти десятков. Сотня и еще одна сотня — 2 сотни. Прибавим еще одну сотню — 3 сотни.
Вот как происходит запись трехзначного числа: натуральные числа записываются одно за другим слева направо.
Крайнее правое однозначное число указывает на количество единиц, следующее — на количество десятков, крайнее левое — на количество сотен. Цифра 0 показывает отсутствие единиц или десятков. Поэтому 506 — это 5 сотен, 0 десятков и 6 единиц.
Точно так же определяются четырехзначные, пятизначные, шестизначные и другие натуральные числа.
Многозначные натуральные числа
Многозначные натуральные числа состоят из двух и более знаков.
1 000 — это множество с десятью сотнями, 1 000 000 состоит из тысячи тысяч, а один миллиард — это тысяча миллионов. Тысяча миллионов, только представьте! То есть мы можем рассмотреть любое многозначное натуральное число как набор однозначных натуральных чисел.
Например, 2 873 206 содержит в себе: 6 единиц, 0 десятков, 2 сотни, 3 тысячи, 7 десятков тысяч, 8 сотен тысяч и 2 миллиона.
Сколько всего натуральных чисел?
Однозначных 9, двухзначных 90, трехзначных 900 и т.д.
Свойства натуральных чисел
Об особенностях натуральных чисел мы уже знаем. А теперь подробно расскажем про их свойства:
| множество натуральных чисел | бесконечно и начинается с единицы (1) |
| за каждым натуральным числом следует другое | оно больше предыдущего на 1 |
| результат деления натурального числа на единицу (1) | само натуральное число: 5 : 1 = 5 |
| результат деления натурального числа на него самого | единица (1): 6 : 6 = 1 |
| переместительный закон сложения | от перестановки мест слагаемых сумма не меняется: 4 + 3 = 3 + 4 |
| сочетательный закон сложения | результат сложения нескольких слагаемых не зависит от порядка действий: (2 + 3) + 4 = 2 + (3 + 4) |
| переместительный закон умножения | от перестановки мест множителей произведение не изменится: 4 × 5 = 5 × 4 |
| сочетательный закон умножения | результат произведения множителей не зависит от порядка действий; можно хоть так, хоть эдак: (6 × 7) × 8 = 6 × (7 × 8) |
| распределительный закон умножения относительно сложения | чтобы умножить сумму на число, нужно каждое слагаемое умножить на это число и полученные результаты сложить: 4 × (5 + 6) = 4 × 5 + 4 × 6 |
| распределительный закон умножения относительно вычитания | чтобы умножить разность на число, можно умножить на это число отдельно уменьшаемое и вычитаемое, а затем из первого произведения вычесть второе: 3 × (4 − 5) = 3 × 4 − 3 × 5 |
| распределительный закон деления относительно сложения | чтобы разделить сумму на число, можно разделить на это число каждое слагаемое и сложить полученные результаты: (9 + 8) : 3 = 9 : 3 + 8 : 3 |
| распределительный закон деления относительно вычитания | чтобы разделить разность на число, можно разделить на это число сначала уменьшаемое, а затем вычитаемое, и из первого произведения вычесть второе: (5 − 3) : 2 = 5 : 2 − 3 : 2 |
Разряды натурального числа и значение разряда
Напомним, что от позиции, на которой стоит цифра в записи числа, зависит ее значение. Так, например, 1 123 содержит в себе: 3 единицы, 2 десятка, 1 сотню, 1 тысячу. При этом можно сформулировать иначе и сказать, что в заданном числе 1 123 цифра 3 располагается в разряде единиц, 2 в разряде десятков, 1 в разряде сотен и 1 служит значением разряда тысяч.
Разряд — это позиция, место расположения цифры в записи натурального числа.
У каждого разряда есть свое название. Слева всегда располагаются старшие разряды, а справа — младшие. Чтобы быстрее запомнить, можно использовать таблицу.
Количество разрядов всегда соответствует количеству знаков в числе. В этой таблице есть названия всех разрядов для числа, которое состоит из 15 знаков. У следующих разрядов также есть названия, но они используются крайне редко.
Низший (младший) разряд многозначного натурального числа — разряд единиц.
Высший (старший) разряд многозначного натурального числа — разряд, соответствующий крайней левой цифре в заданном числе.
Вы наверняка заметили, что в учебниках часто ставят небольшие пробелы при записи многозначных чисел. Так делают, чтобы натуральные числа было удобно читать. А еще — чтобы визуально разделить разные классы чисел.
Класс — это группа разрядов, которая содержит в себе три разряда: единицы, десятки и сотни.
Десятичная система счисления
Люди в разные времена использовали разные методы записи чисел. И каждая система счисления имеет свои правила и особенности.
Десятичная система счисления — самая распространенная система счисления, в которой для записи чисел используют десять знаков: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
В десятичной системе значение одной и той же цифры зависит от ее позиции в записи числа. Например, число 555 состоит из трех одинаковых цифр. В этом числе первая слева цифра означает пять сотен, вторая — пять десятков, а третья — пять единиц. Так как значение цифры зависит от ее позиции, десятичную систему счисления называют позиционной.
Вопрос для самопроверки
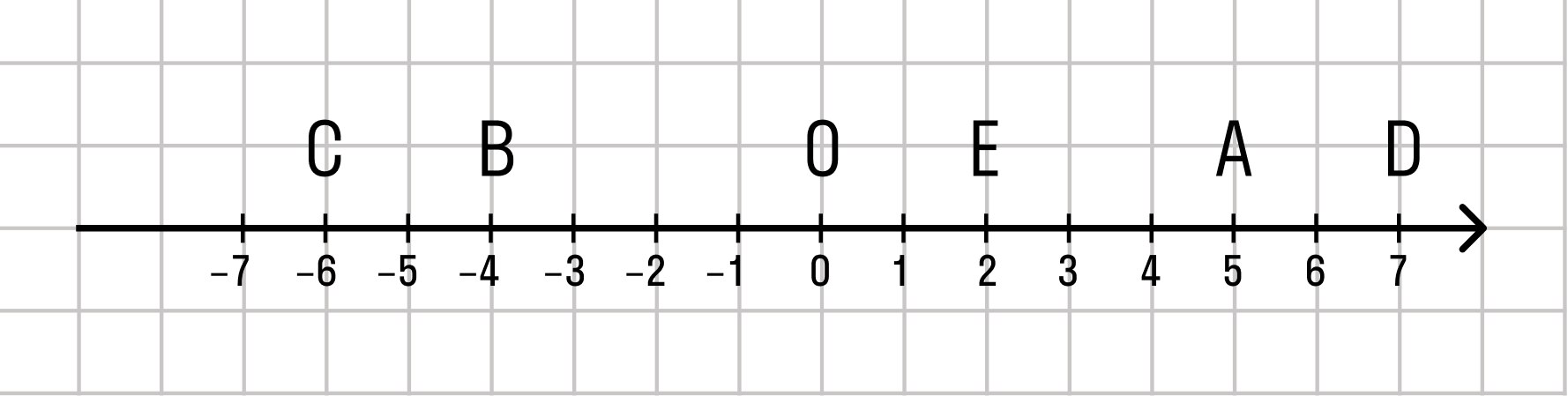
Сколько натуральных чисел можно отметить на координатном луче между точками с координатами:
Число
Число — абстракция, используемая для количественной характеристики объектов. Возникнув ещё в первобытном обществе из потребностей счёта, понятие числа изменялось и обогащалось и превратилось в важнейшее математическое понятие.
Содержание
Появление чисел
Интуитивное представление о числе, по–видимому, так же старо, как и само человечество, хотя с достоверностью проследить все ранние этапы его развития в принципе невозможно. Прежде чем человек научился считать или придумал слова для обозначения чисел, он, несомненно, владел наглядным, интуитивным представлением о числе, позволявшим ему различать одного человека и двух людей или двух и многих людей. То, что первобытные люди сначала знали только “один”, “два” и “много”, подтверждается тем, что в некоторых языках, например в греческом, существуют три грамматические формы: единственного числа, двойственного числа и множественного числа. Позднее человек научился делать различия между двумя и тремя деревьями и между тремя и четырьмя людьми. Счет изначально был связан с вполне конкретным набором объектов, и самые первые названия чисел были прилагательными. Например, слово “три” использовалось только в сочетаниях “три дерева” или “три человека”; представление о том, что эти множества имеют между собой нечто общее – понятие троичности – требует высокой степени абстракции. О том, что счет возник раньше появления этого уровня абстракции, свидетельствует тот факт, что слова “один” и “первый”, равно как “два” и “второй”, во многих языках не имеют между собой ничего общего, в то время как лежащие за пределами первобытного счета “один”, “два”, “много”, слова “три” и “третий”, “четыре” и “четвертый” ясно указывают на взаимосвязь между количественными и порядковыми числительными.
Названия чисел, выражающие весьма абстрактные идеи, появились, несомненно, позже, чем первые грубые символы для обозначения числа объектов в некоторой совокупности. В глубокой древности примитивные числовые записи делались в виде зарубок на палке, узлов на веревке, выложенных в ряд камешков, причем подразумевалось, что между пересчитываемыми элементами множества и символами числовой записи существует взаимно однозначное соответствие. Но для чтения таких числовых записей названия чисел непосредственно не использовались. Ныне мы с первого взгляда распознаем совокупности из двух, трех и четырех элементов; несколько труднее распознаются на взгляд наборы, состоящие из пяти, шести или семи элементов. А за этой границей установить на глаз их число практически уже невозможно, и нужен анализ либо в форме счета, либо в определенном структурировании элементов. Счет на бирках, по–видимому, был первым приемом, который использовался в подобных случаях: зарубки на бирках располагались определенными группами подобно тому, как при подсчете избирательных бюллетеней их часто группируют пачками по пять или десять штук. Очень широко был распространен счет на пальцах, и вполне возможно, что названия некоторых чисел берут свое начало именно от этого способа подсчета.
Важная особенность счета заключается в связи названий чисел с определенной схемой счета. Например, слово “двадцать три” – не просто термин, означающий вполне определенную (по числу элементов) группу объектов; это термин составной, означающий “два раза по десять и три”. Здесь отчетливо видна роль числа десять как коллективной единицы или основания; и действительно, многие считают десятками, потому что, как отметил еще Аристотель, у нас по десять пальцев на руках и на ногах. По той же причине использовались основания пять или двадцать. На очень ранних стадиях развития истории человечества за основания системы счисления принимались числа 2, 3 или 4; иногда для некоторых измерений или вычислений использовались основания 12 и 60.
Считать человек начал задолго до того, как он научился писать, поэтому не сохранилось никаких письменных документов, свидетельствовавших о тех словах, которыми в древности обозначали числа. Для кочевых племен характерны устные названия чисел, что же касается письменных, то необходимость в них появилась лишь с переходом к оседлому образу жизни, образованием земледельческих сообществ. Возникла и необходимость в системе записи чисел, и именно тогда было заложено основание для развития математики.
Основные виды чисел
Рациональные числа — числа, представимы в виде дроби m/n (n≠0), где m и n — целые числа. Для рациональных чисел определены все четыре «классические» арифметические действия: сложение, вычитание, умножение и деление (кроме деления на ноль). Для обозначения рациональных чисел используется знак Q.
Действительные (вещественные) числа представляют собой расширение множества рациональных чисел, замкнутое относительно некоторых (важных для математического анализа) операций предельного перехода. Множество вещественных чисел обозначается R. Кроме рациональных чисел, R включает множество иррациональных чисел, не представимых в виде отношения целых. Кроме подразделения на рациональные и иррациональные, действительные числа также подразделяются на алгебраические и трансцендентные. При этом каждое трансцендентное число является иррациональным, каждое рациональное число — алгебраическим.
Комплексные числа C, являющиеся расширением множества действительных чисел. Они могут быть записаны в виде z = x + iy, где i — т. н. мнимая единица, для которой выполняется равенство i^2=-1. Комплексные числа используются при решении задач квантовой механики, гидродинамики, теории упругости и пр.
Кватернионы представляющие собой разновидность гиперкомплексных чисел. Множество кватернионов обозначается H. Кватернионы в отличии от комплексных чисел не коммутативны относительно умножения.
В свою очередь октавы O, являющиеся расширением кватернионов, уже теряют свойство ассоциативности.
В отличие от октав, седенионы S не обладают свойством альтернативности, но сохраняют свойство степенной ассоциативности.
Представление чисел в памяти компьютера
Для представления целого положительного числа х в памяти компьютера, оно переводится в двоичную систему счисления. Полученное число в двоичной системе счисления х2 представляет собой машинную запись соответствующего десятичного числа х10. Для записи отрицательных чисел используется т. н. дополнительный код числа, который получается путём прибавления единицы к инвертированному представлению модуля данного отрицательного числа в двоичной системе счисления.
Представление действительных чисел в памяти компьютера (в вычислительной технике для их обозначения используется термин число с плавающей запятой) имеет некоторые ограничения связанные с используемой системой счисления, а также, ограниченностью объёма памяти выделяемого под числа. Так, лишь некоторые из действительных чисел могут быть без потерь в точности представлены в памяти компьютера. В наиболее распространённой схеме число с плавающей запятой записывается в виде блока битов часть из которых представляют собой мантиссу числа, часть — степень, а один бит выделяется для представления знака числа (в случае необходимости знаковый бит может отсутствовать).
Действительные числа
Определение действительных чисел
Рациональные числа объединяют в себе целые числа и дробные числа. А действительные числа объединяют рациональные и иррациональные числа. Отсюда сформулируем определение действительных чисел:
Рациональное число — это число, которое можно представить в виде положительной или отрицательной обыкновенной дроби или числа ноль. Множество рациональных чисел —
Иррациональное число — это число, которое невозможно выразить в форме деления двух целых чисел, то есть в рациональной дроби m/n. Оно может быть выражено в форме бесконечной непериодической десятичной дроби. Множество иррациональных чисел —
Множество действительных чисел состоит из множества рациональных чисел вместе с множеством иррациональных чисел. Это множество R иначе обозначается как область действительных чисел (-∞; +∞). Можно записать так, что R есть объединение двух множеств: рациональных и иррациональных чисел:
Так как любое рациональное число может быть записано в виде конечной десятичной дроби или бесконечной периодической дроби, а иррациональные числа представляются бесконечными непериодическими десятичными дробями, то определение действительных чисел можно сформулировать по-другому.
Действительные числа — это числа, которые можно записать в виде конечной или бесконечной, периодической или непериодической десятичной дроби. Их иногда называют вещественными.
Примеры действительных чисел:
Число нуль также является действительным числом, так как 0 — рациональное число.
Из определения действительных чисел можно сделать вывод, что существуют как положительные, так и отрицательные действительные числа, а нуль — ни положительное, ни отрицательное действительное число.
При помощи действительных чисел можно описать величины, значения которых могут изменяться непрерывно. Проще говоря, действительные числа дают возможность численно выражать значение непрерывно изменяющейся величины через единичное значение этой величины.
Действительные числа на координатной прямой
Координатная прямая — это прямая, которая изображается с определенной точкой отсчета, которая принимается за 0, единичным отрезком и заданным направлением движения.
Интересный факт: действительные числа заполняют каждую точку координатной прямой.
Каждой точке координатной прямой соответствует единственное действительное число — координата этой точки. При этом каждому действительному числу соответствует единственная точка на координатной прямой. То есть, между действительными числами и точками координатной прямой существует взаимно однозначное соответствие.
Представления действительных чисел
По определению действительными числами являются:
Часто можно встретить действительные числа в виде корней, степеней, логарифмов и др. Кроме того, сумма, разность, произведение и частное действительных чисел также представляют собой действительные числа.
Также из действительных чисел с помощью арифметических знаков, знаков корня, степеней, логарифмических, тригонометрических функций можно составлять числовые выражения, значения которых также будут действительными числами. Например, значения выражений
будут действительные числа.
Сравнение действительных чисел
Любые действительные числа можно сравнивать. Для сравнения действительных чисел есть два способа: