какие виды матриц существуют

Какие виды матриц существуют

Матрицей размерности m×n называется таблица чисел a_ij, содержащая m строк и n столбцов. Числа a_ij называются элементами этой матрицы, где i – номер строки, j – номер столбца, на пересечении которых стоит данный элемент. Матрица, содержащая m строк и n столбцов, имеет вид:

Виды матриц:
1) при m=n – квадратная, в данном случае n называют порядком матрицы;
2) квадратная матрица, у которой все недиагональные элементы равны нулю – диагональная;
3) диагональная матрица, у которой все диагональные элементы равны единице – единичная и обозначается E;
4) при n≠m – прямоугольная;
5) при m=1 – матрица-строка (вектор-строка);
6) при n=1 – матрица-столбец (вектор-столбец);
7) при всех a_ij =0 – нулевая матрица.

Заметим, что основной числовой характеристикой квадратной матрицы является ее определитель. Определитель, соответствующий матрице n-го по-порядка, также имеет n-ый порядок.

Дадим ряд необходимых определений.

Определителем матрицы 2-го порядка называется число

Минором М_ij элемента a_ij матрицы n-го порядка А называется определитель матрицы (n-1)-го порядка, полученной из матрицы А путем вычеркивания i-ой строки и j-го столбца.

1. При транспонировании матрицы ее определитель не меняется.

2. При перестановке двух строк (столбцов) матрицы ее определитель меняет знак.

3. Определитель, имеющий две пропорциональные (равные) строки (столбца), равен нулю.

4. Общий множитель элементов какой-либо строки (столбца) определителя можно вынести за знак определителя.

5. Если элементы какой-либо строки (столбца) определителя представляют собой сумму двух слагаемых, то определитель может быть разложен на сумму двух соответствующих определителей.

6. Определитель не изменится, если к элементам любой его строки (столбца) прибавить соответствующие элементы другой его строки (столбца), предварительно умноженные на любое число.

7. Определитель матрицы равен сумме произведений элементов любой его строки (столбца) на алгебраические дополнения этих элементов.

Поясним данное свойство на примере определителя 3-го порядка. В данном случае свойство 7 означает, что

Свойство 7 представляет собой теорему о разложении определителя, сформулированную Лапласом.

8. Сумма произведений элементов какой-либо строки (столбца) определителя на алгебраические дополнения соответствующих элементов другой его строки (столбца) равна нулю.

Последнее свойство часто называют псевдоразложением определителя.

Источник

Матрица (математика)

Из Википедии — свободной энциклопедии

Матрицы широко применяются в математике для компактной записи систем линейных алгебраических или дифференциальных уравнений. В этом случае количество строк матрицы соответствует числу уравнений, а количество столбцов — количеству неизвестных. В результате решение систем линейных уравнений сводится к операциям над матрицами.

Для матрицы определены следующие алгебраические операции:

Относительно сложения матрицы образуют абелеву группу; если же рассматривать ещё и умножение на скаляр, то матрицы образуют модуль над соответствующим кольцом (векторное пространство над полем). Множество квадратных матриц замкнуто относительно матричного умножения, поэтому квадратные матрицы одного размера образуют ассоциативное кольцо с единицей относительно матричного сложения и матричного умножения.

Доказано, что каждому линейному оператору, действующему в n-мерном линейном пространстве, можно сопоставить единственную квадратную матрицу порядка n; и обратно — каждой квадратной матрице порядка n может быть сопоставлен единственный линейный оператор, действующий в этом пространстве. [2] Свойства матрицы соответствуют свойствам линейного оператора. В частности, собственные числа матрицы — это собственные числа оператора, отвечающие соответствующим собственным векторам.

То же можно сказать о представлении матрицами билинейных (квадратичных) форм.

В математике рассматривается множество различных типов и видов матриц. Таковы, например, единичная, симметричная, кососимметричная, верхнетреугольная (нижнетреугольная) и т. п. матрицы.

Особое значение в теории матриц занимают всевозможные нормальные формы, то есть канонический вид, к которому можно привести матрицу заменой координат. Наиболее важной (в теоретическом значении) и проработанной является теория жордановых нормальных форм. На практике, однако, используются такие нормальные формы, которые обладают дополнительными свойствами, например, устойчивостью.

Источник

Виды матриц и для чего они нужны простыми словами

Обновлено: 12 Августа 2021

При решении алгебраических или дифференциальных уравнений студенты сталкиваются с понятием матрицы. Этот термин используется в программировании, электронике, фотоискусстве, но основная область применения — математика. Рассмотрим, что это такое, как применяется и какие операции позволяет осуществить.

Что такое матрицы в математике

Матрица в математике — это абстрактный объект, имеющий вид таблицы чисел или других математических величин. Чаще таблица прямоугольная, но встречаются и другие виды (квадратные, треугольные).

Обычно матрица называется заглавной буквой латинского алфавита: матрица A, матрица B. В таблице есть строки (их количество называется m) и столбцы (их количество называется n). Количество строк и столбцов определяет размер матрицы и может называться порядком. Матрицы такого типа называются матрицами строения m×n, или размера m×n, или порядка m×n.

Элементы матрицы, т.е. числа или остальные величины, называются строчной буквой. Они имеют 2 нижних индекса, необходимых для определения их положения в матрице. Например, элемент a13 располагается на пересечении 2 строки и 3 столбца. Значения элемента а13 читаются по-отдельности, не как целое число: «а один-три».

Откуда они взялись и чем полезны

Первые упоминания матрицы появились в Древнем Китае. Это была квадратная таблица, получившая название магического или волшебного квадрата. Самым древним и известным считается квадрат 3×3, датируемый около 2200 г до н.э. Он был высечен на панцире черепахи. В Китае его называют квадрат Ло Шу, а в Западной Европе — «Печать Сатурна».

Таким же древним является квадрат, найденный в Кхаджурахо, столице средневекового государства Чандела (IX–XIII вв.) в Центральной Индии. Это первый из «дьявольских квадратов». Также он называется пандиагональным.

В древности матрицы были необходимы преимущественно для решения линейных уравнений. Когда матрицы появились в арабских странах, стали разрабатываться принципы работы с ними, в том числе, принцип сложения. В XVIII веке швейцарский математик, «отец линейной алгебры» Габриэль Крамер опубликовал правило Крамера. Это способ решения систем линейных уравнений с помощью матрицы.

Способ Крамера не подходит для решения тех систем линейных уравнений, в которых может быть бесконечное множество решений.

В следующем веке появляется метод немецкого математика Карла Фридриха Гаусса. Этот способ решения алгебраических уравнений не является открытием ученого. Впервые о методе Гаусса написали в китайском трактате «Математика в девяти книгах», а сам он только привел способ в удобную форму.

Для решения уравнений таким способом необходимо записать расширенную матрицу системы.

В отличие от метода Крамера, правило Гаусса можно использовать для решения любых систем линейных уравнений.

Детальная разработка теории матриц активно продолжилась с середины XIX века. Наиболее значимые ученые: Уильям Гамильтон, Артур Кэли, Карл Вейерштрасс, Мари Энмон Камиль Жордан, Фердинанд Георг Фробениус.

Сам термин «матрица» предложил английский математик Джеймс Сильвестр в 1850 г.

В наше время матрицы используются не только для записи и решения систем линейных уравнений. Списки, статистические данные, табеля с информацией — все это в какой-то степени матрица. Их применяют для упрощения подачи и работы с информацией в любой сфере. Например, таблица продаж, где указан год (первый столбец), вид продукции (первая строка), а остальные значения — количество проданных единиц.

Обозначения матриц

Помимо самого термина «матрицы», при их решении нужно знать и другие обозначения.

Элементы матрицы — любые математические объекты: числа, переменные, другие матрицы. Элемент обозначается как a_ab, где a — номер строки расположения элемента, b — номер столбца.

Главная диагональ матрицы — диагональ, пересекающая квадратную матрицу из верхнего левого угла в нижний правый угол (квадратные матрицы имеют одинаковое количество строк и столбцов). Прямоугольные матрицы также могут иметь диагонали: они пересекают элементы с одинаковыми индексами.

Побочная диагональ матрицы — диагональ, пересекающая верхний правый и нижний левый углы. Для прямоугольного вида матриц понятие «побочные диагонали» не используется.

Диагональные элементы — числа и другие математические величины матрицы, расположенные на главной диагонали.

Размер (порядок) матрицы — произведение количества строк на количество столбцов: m×n. Например, если матрица содержит 2 строки и 3 столбца, то ее обозначают матрицей 2×3.

След матрицы — сумма элементов матрицы, расположенных на главной диагонали. Обозначается как Sp (А) или Tr (A), где A — название матрицы.

Равные матрицы — матрицы, у которых соответствующие элементы равны.

Виды матриц, какие бывают

В математике существует несколько видов матриц в зависимости от их размера.

Также различают матрицы по значениям их элементов.

Треугольная матрица всегда квадратная: m=n.

Кососимметрическая матрица всегда квадратная.

Применение матриц в математико-экономическом моделировании

С древности и по настоящее время матрицы используются для решения и удобной записи системы линейных алгебраических или дифференциальных уравнений. Но их также применяют в математико-экономическом моделировании для структурирования данных и комфортной работы с ними.

Наиболее популярной является матричная модель экономики «затраты–выпуск». Ее внедрил Василий Леонтьев — американский экономист. За развитие этого метода он получил нобелевскую премию: матричная модель упростила решение некоторых экономических проблем. В последствии Леонтьева стали называть «апостолом планирования».

Суть модели «затраты–выпуск» в том, что экономист разделил производственный сектор экономики на отрасли, число которых обозначается n. 1 отрасль — 1 вид продукции. Значит, n количество отраслей выпускает n количество продуктов. Это приводит к появлению межотраслевых связей: одна отрасль заимствует у другой продукт и использует в процессе производства своей продукции. Данная балансовая модель представлена в виде системы линейных уравнений, решаемых с помощью матрицы.

Какие операции можно производить с матрицами

С матрицами можно проводить несколько операций.

При умножении матрицы нельзя менять местами.

Примеры решения задач на матрицы

Пример решения задачи на умножение.

Найдем значение каждого элемента:

Пример решения задачи на умножение матрицы на число 5.

Учитесь работать с матрицами и продолжайте осваивать математику, а если задач накопилось слишком много и «горят» сроки, вам поможет сервис Феникс.Хелп. Обращайтесь!

Источник

Виды матриц и их свойства

В данной презинтации я пакажу вам виды матриц и их свойства

Содержимое разработки

Тема 1 . «Матрицы и действия над ними»

Прямоугольная таблица чисел вида

Главная диагональ матрицы

Побочная диагональ матрицы

Квадратные матрицы вида

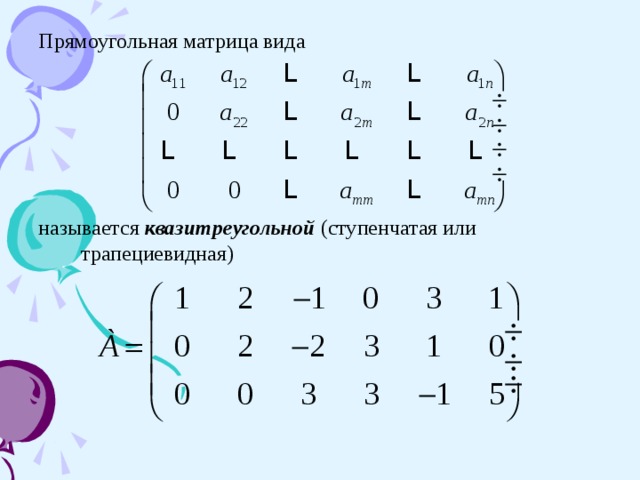
Прямоугольная матрица вида

называется квазитреугольной (ступенчатая или трапециевидная)

Матрица, состоящая из одного столбца называется матрицей-столбцом или столбцевой матрицей

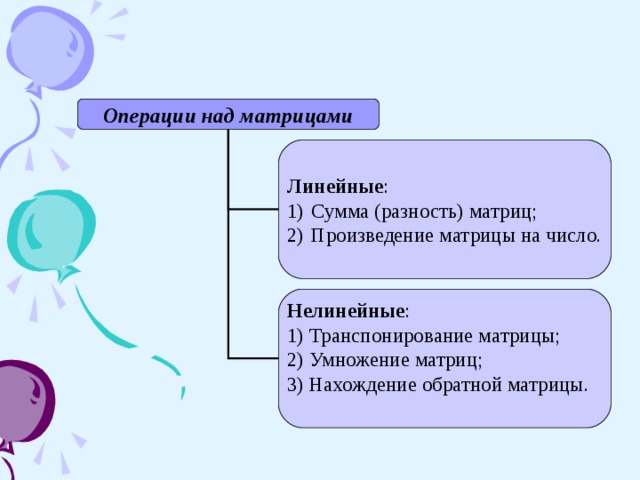
Операции над матрицами

1) Транспонирование матрицы;

2) Умножение матриц;

3) Нахождение обратной матрицы.

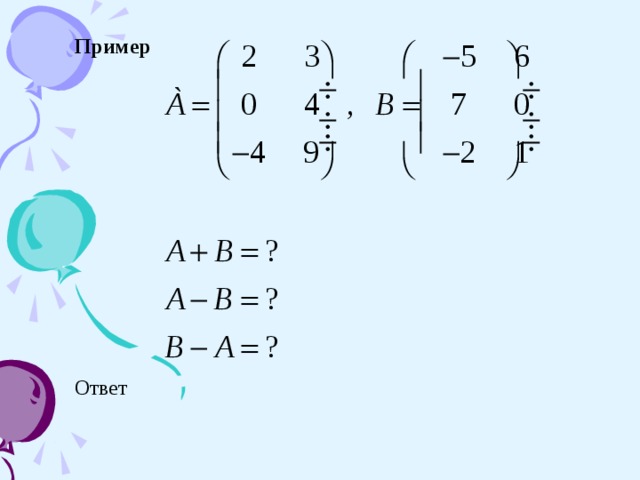
Суммой (разностью) двух матриц одинаковой размерности называется матрица, элементы которой равны сумме (разности) соответствующих элементов матриц слагаемых.

Произведением матрицы на число называется матрица, полученная из данной умножением всех ее элементов на число.

Линейные операции обладают следующими свойствами :

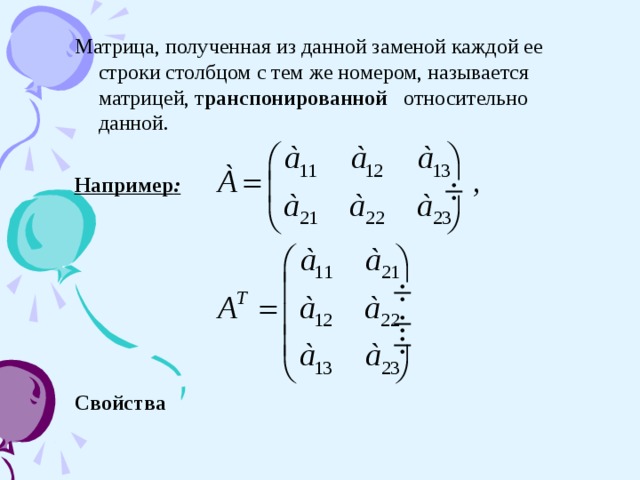
Матрица, полученная из данной заменой каждой ее строки столбцом с тем же номером, называется матрицей, т ранспонированной относительно данной.

Умножение матриц определяется для согласованных матриц.

Источник

Какие виды матриц существуют

ОПРЕДЕЛЕНИЕ МАТРИЦЫ. ВИДЫ МАТРИЦ

Матрицей размером m×n называется совокупность m·n чисел, расположенных в виде прямоугольной таблицы из m строк и n столбцов. Эту таблицу обычно заключают в круглые скобки. Например, матрица может иметь вид:

Для краткости матрицу можно обозначать одной заглавной буквой, например, А или В.

В общем виде матрицу размером m×n записывают так

.

Числа, составляющие матрицу, называются элементами матрицы. Элементы матрицы удобно снабжать двумя индексами a_ij: первый указывает номер строки, а второй – номер столбца. Например, a₂₃ – элемент стоит во 2-ой строке, 3-м столбце.

Если в матрице число строк равно числу столбцов, то матрица называется квадратной, причём число ее строк или столбцов называется порядком матрицы. В приведённых выше примерах квадратными являются вторая матрица – её порядок равен 3, и четвёртая матрица – её порядок 1.

Матрица, в которой число строк не равно числу столбцов, называется прямоугольной. В примерах это первая матрица и третья.

Различаются также матрицы, имеющие только одну строку или один столбец.

Матрица, у которой всего одна строка , называется матрицей – строкой (или строковой), а матрица, у которой всего один столбец, матрицей – столбцом.

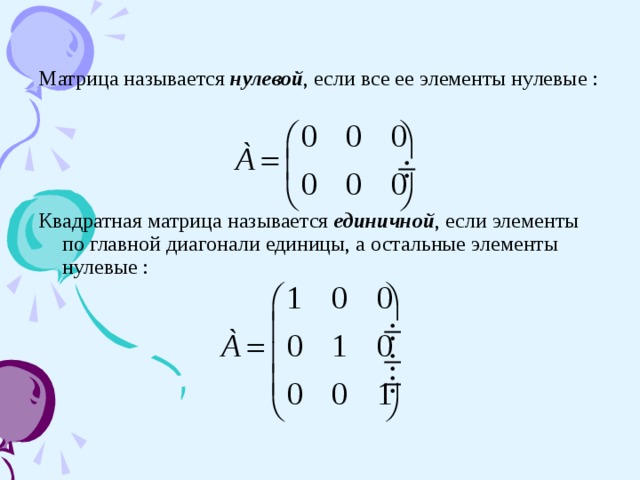
Матрица, все элементы которой равны нулю, называется нулевой и обозначается (0), или просто 0. Например,

.

Главной диагональю квадратной матрицы назовём диагональ, идущую из левого верхнего в правый нижний угол.

Квадратная матрица, у которой все элементы, лежащие ниже главной диагонали, равны нулю, называется треугольной матрицей.

.

Квадратная матрица, у которой все элементы, кроме, быть может, стоящих на главной диагонали, равны нулю, называется диагональной матрицей. Например, или .

Диагональная матрица, у которой все диагональные элементы равны единице, называется единичной матрицей и обозначается буквой E. Например, единичная матрица 3-го порядка имеет вид .

ДЕЙСТВИЯ НАД МАТРИЦАМИ

Равенство матриц. Две матрицы A и B называются равными, если они имеют одинаковое число строк и столбцов и их соответствующие элементы равны a_ij = b_ij. Так если и , то A=B, если a₁₁ = b₁₁, a₁₂ = b₁₂, a₂₁ = b₂₁ и a₂₂ = b₂₂.

Транспонирование. Рассмотрим произвольную матрицу A из m строк и n столбцов. Ей можно сопоставить такую матрицу B из n строк и m столбцов, у которой каждая строка является столбцом матрицы A с тем же номером (следовательно, каждый столбец является строкой матрицы A с тем же номером). Итак, если , то .

Эту матрицу B называют транспонированной матрицей A, а переход от A к B транспонированием.

Связь между матрицей A и её транспонированной можно записать в виде .

Например. Найти матрицу транспонированную данной.

Сложение матриц. Пусть матрицы A и B состоят из одинакового числа строк и одинакового числа столбцов, т.е. имеют одинаковые размеры. Тогда для того, чтобы сложить матрицы A и B нужно к элементам матрицы A прибавить элементы матрицы B, стоящие на тех же местах. Таким образом, суммой двух матриц A и B называется матрица C, которая определяется по правилу, например,

Примеры. Найти сумму матриц:

Легко проверить, что сложение матриц подчиняется следующим законам: коммутативному A+B=B+A и ассоциативному (A+B)+C=A+(B+C).

Умножение матрицы на число. Для того чтобы умножить матрицу A на число k нужно каждый элемент матрицы A умножить на это число. Таким образом, произведение матрицы A на число k есть новая матрица, которая определяется по правилу или .

Для любых чисел a и b и матриц A и B выполняются равенства:

.

Матрицу C найти нельзя, т.к. матрицы A и B имеют разные размеры.

Умножение матриц. Эта операция осуществляется по своеобразному закону. Прежде всего, заметим, что размеры матриц–сомножителей должны быть согласованы. Перемножать можно только те матрицы, у которых число столбцов первой матрицы совпадает с числом строк второй матрицы (т.е. длина строки первой равна высоте столбца второй). Произведением матрицы A не матрицу B называется новая матрица C=AB, элементы которой составляются следующим образом:

.

Таким образом, например, чтобы получить у произведения (т.е. в матрице C) элемент, стоящий в 1-ой строке и 3-м столбце c₁₃, нужно в 1-ой матрице взять 1-ую строку, во 2-ой – 3-й столбец, и затем элементы строки умножить на соответствующие элементы столбца и полученные произведения сложить. И другие элементы матрицы-произведения получаются с помощью аналогичного произведения строк первой матрицы на столбцы второй матрицы.

В общем случае, если мы умножаем матрицу A = (a_ij) размера m×n на матрицу B = (b_ij) размера n×p, то получим матрицу C размера m×p, элементы которой вычисляются следующим образом: элемент c_ij получается в результате произведения элементов i-ой строки матрицы A на соответствующие элементы j-го столбца матрицы B и их сложения.

Из этого правила следует, что всегда можно перемножать две квадратные матрицы одного порядка, в результате получим квадратную матрицу того же порядка. В частности, квадратную матрицу всегда можно умножить саму на себя, т.е. возвести в квадрат.

Другим важным случаем является умножение матрицы–строки на матрицу–столбец, причём ширина первой должна быть равна высоте второй, в результате получим матрицу первого порядка (т.е. один элемент). Действительно,

.

.

, B·A – не имеет смысла.

Таким образом, эти простые примеры показывают, что матрицы, вообще говоря, не перестановочны друг с другом, т.е. A∙B ≠ B∙A. Поэтому при умножении матриц нужно тщательно следить за порядком множителей.

Можно проверить, что умножение матриц подчиняется ассоциативному и дистрибутивному законам, т.е. (AB)C=A(BC) и (A+B)C=AC+BC.

Легко также проверить, что при умножении квадратной матрицы A на единичную матрицу E того же порядка вновь получим матрицу A, причём AE=EA=A.

Можно отметить следующий любопытный факт. Как известно произведение 2-х отличных от нуля чисел не равно 0. Для матриц это может не иметь места, т.е. произведение 2-х не нулевых матриц может оказаться равным нулевой матрице.

Например, если , то

.

Пусть дана матрица второго порядка – квадратная матрица, состоящая из двух строк и двух столбцов .

Определителем второго порядка, соответствующим данной матрице, называется число, получаемое следующим образом: a₁₁a₂₂ – a₁₂a₂₁.

Определитель обозначается символом .

Итак, для того чтобы найти определитель второго порядка нужно из произведения элементов главной диагонали вычесть произведение элементов по второй диагонали.

Примеры. Вычислить определители второго порядка.

Аналогично можно рассмотреть матрицу третьего порядка и соответствующий ей определитель.

Определителем третьего порядка, соответствующим данной квадратной матрице третьего порядка, называется число, обозначаемое и получаемое следующим образом:

.

Таким образом, эта формула даёт разложение определителя третьего порядка по элементам первой строки a₁₁, a₁₂, a₁₃ и сводит вычисление определителя третьего порядка к вычислению определителей второго порядка.

Примеры. Вычислить определитель третьего порядка.

.

Аналогично можно ввести понятия определителей четвёртого, пятого и т.д. порядков, понижая их порядок разложением по элементам 1-ой строки, при этом знаки «+» и «–» у слагаемых чередуются.

Итак, в отличие от матрицы, которая представляют собой таблицу чисел, определитель это число, которое определённым образом ставится в соответствие матрице.

Источник