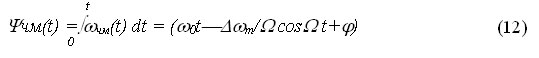Виды модуляции

Виды различных типов модуляции сигналов в примерах.

Частотная модуляция на сегодняшний день является наиболее популярной, она дает возможность передавать в эфире аналоговые звуковые сигналы с высоким качеством. Частотная модуляция в отличии от других видов модуляции отличается высокой помехозащищенностью, устойчивостью к индустриальным и атмосферным помехам.

Приемник с частотным детектором использующий частотную модуляцию регистрирует только изменение частоты принятого сигнала, совершенно не реагируя на паразитную амплитудную модуляцию.
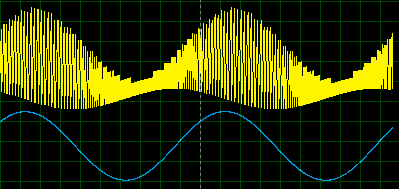
На рисунке ниже продемонстрировано, как происходит модуляция несущей частоты сигнала входным аудиосигналом.

Мы видим, что амплитуда входного модулирующего сигнала (AUDIO OSC) воздействует только на частоту несущей, оставляя неизменным выходной уровень ВЧ сигнала.

Посмотрим на структурную схему ЧМ радиоприемника и вкратце разберем отдельные его узлы.

RF AMP – Входной ВЧ усилитель-преселлектор.
LOCAL OSC – Гетеродин приемника
MIXER – Смеситель (узел, в котором происходит смешивание входного сигнала и сигнала гетеродина)
BPF – Фильтр промежуточной частоты, который выделяет разность частот входного и гетеродинного сигнала, т.е. промежуточную частоту (ПЧ).
IF AMP – Усилитель промежуточной частоты (УПЧ).
LIMITER – Усилитель-ограничитель сигнала ПЧ, в нем подавляются остатки паразитной амплитудной модуляции перед дальнейшим детектированием сигнала.
SLOPE DET – Частотный детектор, или, как его еще называют, детектор отношений. Он реагирует на изменение частоты входного сигнала и преобразует это изменение в амплитуду, зависящую от частоты.
Фильтр промежуточной частоты в приемнике имеет ограниченную полосу пропускания, обеспечивая селективность приемника. Используется для подавления помех со стороны близлежащих сигналов других передатчиков.
Работа фильтра (BPF) промежуточной частоты изображена ниже

АМПЛИТУДНАЯ МОДУЛЯЦИЯ
Амплитудная модуляция по качеству передаваемой информации заметно уступает частотной. Подвержена электромагнитным помехам. Входной звуковой сигнал воздействует на амплитуду несущей частоты передатчика.
Посмотрим, как реализуется данный вид модуляции.

Структурная схема передатчика с амплитудной модуляцией.

Структурная схема приемника амплитудной модуляции.

Как видно из рисунка, схема приемника очень схожа с приемником ЧМ, и отличается лишь тем, что вместо детектора отношений здесь используется амплитудный детектор, который регистрирует изменение уровня амплитуды сигнала промежуточной частоты.

DSB – АМПЛИТУДНАЯ МОДУЛЯЦИЯ С ПОДАВЛЕННОЙ НЕСУЩЕЙ
При таком виде модуляции сигнал несущей частоты на выходе передатчика присутствует только при наличии модулирующего аудиосигнала на входе. В отличие от АМ, здесь энергия передатчика используется более экономично.

SSB — ОДНОПОЛОСНАЯ МОДУЛЯЦИЯ С ПОДАВЛЕННОЙ НЕСУЩЕЙ.
Однополосную модуляцию можно сравнить как с амплитудной, так и с частотной, потому что выходная несущая частота содержит и те, и другие признаки. Она состоит из суммы и разности частот входного и модулирующего сигнала. Чтобы избежать взаимного влияния этой суммы и разности, в передатчике, равно как и в приемнике, используется однополосный фильтр (BPF) промежуточной частоты. Как правило, он настроен либо на верхнюю, либо на нижнюю боковую полосу.
Посмотрим как это выглядит визуально.

Балансный модулятор перемножает аудиосигнал с сигналом гетеродина и отправляет полученный результат на полосовой фильтр.

КВАДРАТУРНАЯ МОДУЛЯЦИЯ
Еще один интересный вид модуляции.
С помощью её можно по одной несущей частоте передатчика передавать сразу два аудиосигнала. Такой вид модуляции используется в стереовещании. Она достигается применением в двойного балансного модулятора (перемножителя).

Сигнал на выходе смесителя (М) состоит из двух одинаковых по частоте сигналов. Но они отличаются тем, что сдвинуты относительно между собой по фазе ровно на 90 градусов. Приемник для такого вида модуляции в качестве детектора использует перемножитель такого же типа, который используется в передатчике.

Источник

Что такое модуляция и разновидности модулированных сигналов?

Общие сведения о модуляции

Модуляция — это процесс преобразования одного или нескольких информационных параметров несущего сигнала в соответствии с мгновенными значениями информационного сигнала.

В результате модуляции сигналы переносятся в область более высоких частот.

Использование модуляции позволяет:

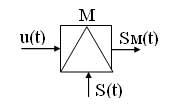
Модуляция осуществляется в устройствах модуляторах. Условное графическое обозначение модулятора имеет вид:

При модуляции на вход модулятора подаются сигналы:

u(t) — модулирующий, данный сигнал является информационным и низкочастотным (его частоту обозначают W или F);

S(t) — модулируемый (несущий), данный сигнал является неинформационным и высокочастотным (его частота обозначается w₀ или f₀);

Sм(t) — модулированный сигнал, данный сигнал является информационным и высокочастотным.

В качестве несущего сигнала может использоваться:

Так как в процессе модуляции изменяются информационные параметры несущего колебания, то название вида модуляции зависит от изменяемого параметра этого колебания.

1. Виды аналоговой модуляции:

2. Виды импульсной модуляции:

Амплитудная модуляция

Амплитудная модуляция — процесс изменения амплитуды несущего сигнала в соответствии с мгновенными значениями модулирующего сигнала.

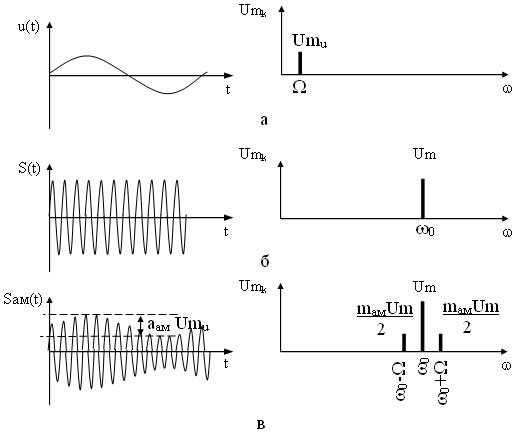
Рассмотрим математическую модель амплитудно-модулированного (АМ) сигнала при гармоническом модулирующем сигнале. При воздействии модулирующего сигнала

на несущее колебание

происходит изменение амплитуды несущего сигнала по закону:

где а_ам — коэффициент пропорциональности амплитудной модуляции.

Подставив (3) в математическую модель (2) получим:

Вынесем Um за скобки:

Отношение а_ам Um_u/Um = m_ам называется коэффициентом амплитудной модуляции. Данный коэффициент не должен превышать единицу, т. к. в этом случае появляются искажения огибающей модулированного сигнала называемые перемодуляцией. С учетом m_ам математическая модель АМ сигнала при гармоническом модулирующем сигнале будет иметь вид:

Если модулирующий сигнал u(t) является негармоническим, то математическая модель АМ сигнала в этом случае будет иметь вид:

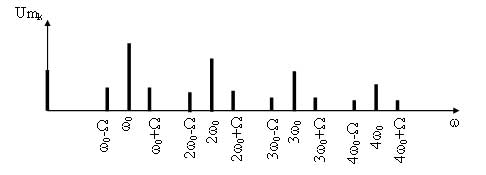
Рассмотрим спектр АМ сигнала для гармонического модулирующего сигнала. Для этого раскроем скобки математической модели модулированного сигнала, т. е. представим его в виде суммы гармонических составляющих.

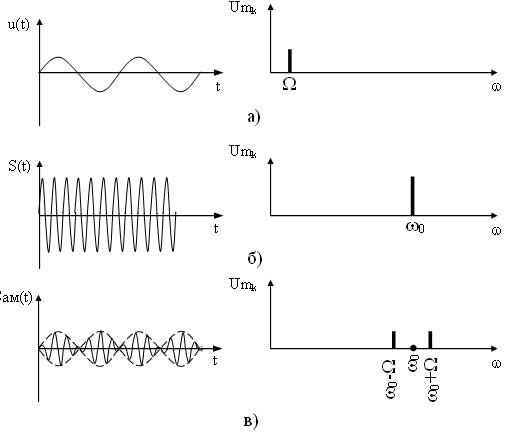
Как видно из выражения в спектре АМ сигнала присутствует три составляющих: составляющая несущего сигнала и две составляющих на комбинационных частотах. Причем составляющая на частоте ?₀—? называется нижней боковой составляющей, а на частоте ?₀ + ? — верхней боковой составляющей. Спектральные и временные диаграммы модулирующего, несущего и амплитудно-модулированного сигналов имеют вид (рисунок 2).

Ширина спектра для данного сигнала будет определятся

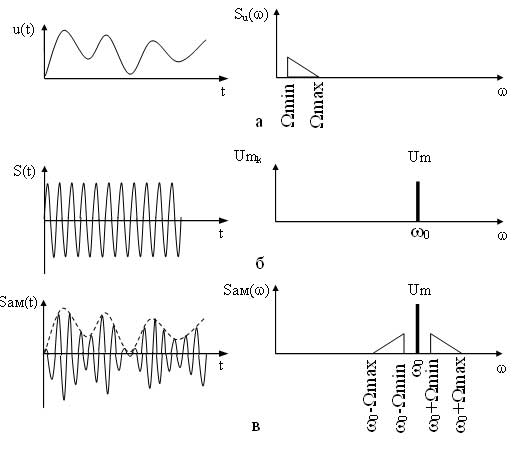
Если же модулирующий сигнал является случайным, то в этом случае в спектре составляющие модулирующего сигнала обозначают символически треугольниками (рисунок 3).

Ширина спектра для данного сигнала будет определятся

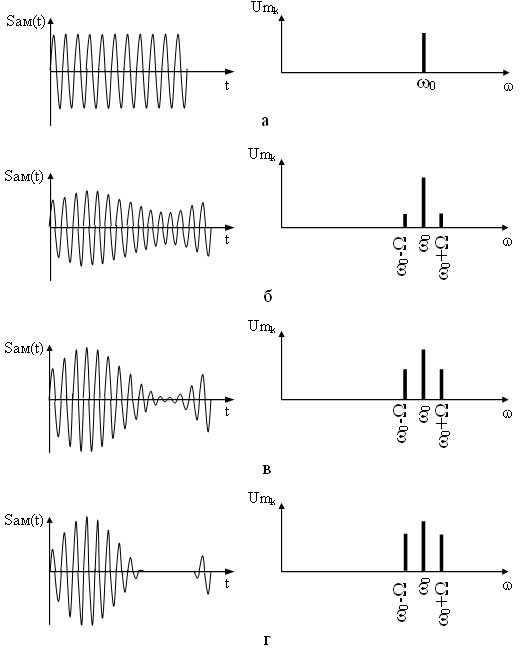
На рисунке 4 приведены временные и спектральные диаграммы АМ сигналов при различных индексах m_ам. Как видно при m_ам=0 модуляция отсутствует, сигнал представляет собой немодулированную несущую, соответственно и спектр этого сигнала имеет только составляющую несущего сигнала (рисунок 4,

а), при индексе модуляции m_ам=1 происходит глубокая модуляция, в спектре АМ сигнала амплитуды боковых составляющих равны половине амплитуды составляющей несущего сигнала (рисунок 4в), данный вариант является оптимальным, т. к. энергия в большей степени приходится на информационные составляющие. На практике добиться коэффициента равного едините тяжело, поэтому добиваются соотношения 0 1 происходит перемодуляция, что, как отмечалось выше, приводит к искажению огибающей АМ сигнала, в спектре такого сигнала амплитуды боковых составляющих превышают половину амплитуды составляющей несущего сигнала (рисунок 4г).

Основными достоинствами амплитудной модуляции являются:

Недостатками этой модуляции являются:

Амплитудная модуляция нашла широкое применение:

Балансная и однополосная модуляция

Как отмечалось выше, одним из недостатков амплитудной модуляции является наличие составляющей несущего сигнала в спектре модулированного сигнала. Для устранения этого недостатка применяют балансную модуляцию. При балансной модуляциипроисходит формирование модулированного сигнала без составляющей несущего сигнала. В основном это осуществляется путем использования специальных модуляторов: балансного или кольцевого. Временная диаграмма и спектр балансно-модулированного (БМ) сигнала представлен на рисунке 5.

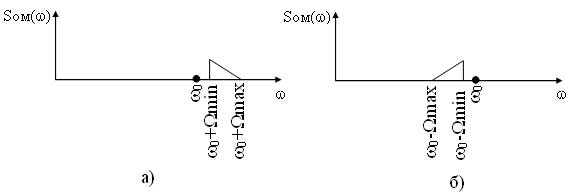
Также особенностью модулированного сигнала является наличие в спектре двух боковых полос несущих одинаковую информацию. Подавление одной из полос позволяет уменьшить спектр модулированного сигнала и, соответственно, увеличить число каналов в линии связи. Модуляция при которой формируется модулированный сигнал с одной боковой полосой (верхней или нижней) называется однополосной. Формирование однополосно-модулированного (ОМ) сигнала осуществляется из БМ сигнала специальными методами, которые рассматриваются ниже. Спектры ОМ сигнала представлены на рисунке 6.

Частотная модуляция

Частотная модуляция — процесс изменения частоты несущего сигнала в соответствии с мгновенными значениями модулирующего сигнала.

Рассмотрим математическую модель частотно-модулированного (ЧМ) сигнала при гармоническом модулирующем сигнале. При воздействии модулирующего сигнала

на несущее колебание

происходит изменение частоты несущего сигнала по закону:

где а_чм — коэффициент пропорциональности частотной модуляции.

Величина Dw_m называется девиацией частоты. Следовательно, девиация частоты показывает наибольшее отклонение частоты модулированного сигнала от частоты несущего сигнала.

называется индексом частотной модуляции.

Учитывая (12) и (13) математическая модель ЧМ сигнала при гармоническом модулирующем сигнале будет иметь вид:

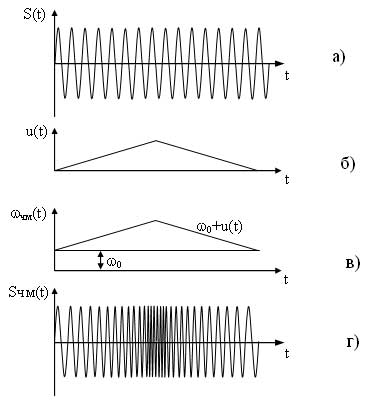
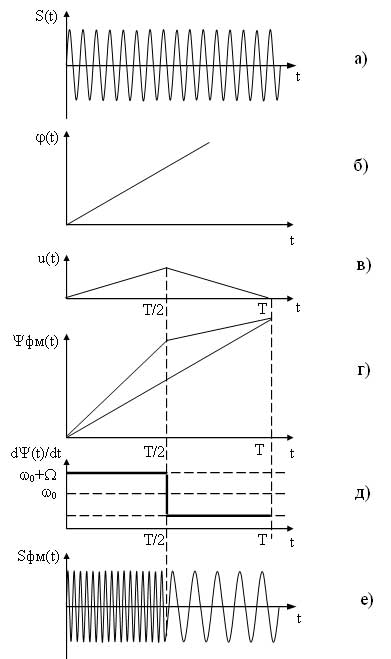
Временные диаграммы, поясняющие процесс формирования частотно-модулированного сигнала приведены на рисунке 7. На первых диаграммах а) и б) представлены соответственно несущий и модулирующий сигналы, на рисунке в) представлена диаграмма показывающая закон изменения частоты ЧМ сигнала. На диаграмме г) представлен частогтно-модулированный сигнал соответствующий заданному модулирующему сигналу, как видно из диаграммы любое изменение амплитуды модулирующего сигнала вызывает пропорциональное изменение частоты несущего сигнала.

Для построения спектра ЧМ сигнала необходимо разложить его математическую модель на гармонические составляющие. В результате разложения получим

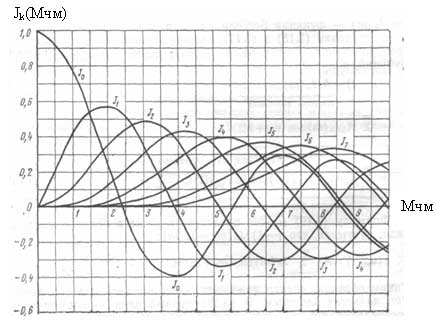
где J_k(Mчм) — коэффициенты пропорциональности.

J_k(Mчм) определяются по функциям Бесселя и зависят от индекса частотной модуляции. На рисунке 8 представлен график содержащий восемь функций Бесселя. Для определения амплитуд составляющих спектра ЧМ сигнала необходимо определить значение функций Бесселя для заданного индекса. Причем как

видно из рисунка различные функции имеют начало в различных значениях Мчм, а следовательно, количество составляющих в спектре будет определятся Мчм (с увеличивается индекса увеличивается и количество составляющих спектра). Например необходимо определить коэффициенты J_k(Мчм) при Мчм=2. По графику видно, что при заданном индексе можно определить коэффициенты для пяти функций (J₀, J₁, J₂, J₃, J₄) Их значение при заданном индексе будет равно: J₀=0,21; J₁=0,58; J₂=0,36; J₃=0,12; J₄=0,02. Все остальные функции начинаются после значения Мчм=2 и равны, соответственно, нулю. Для приведенного примера количество составляющих в спектре ЧМ сигнала будет равно 9: одна составляющая несущего сигнала (Um J₀) и по четыре составляющих в каждой боковой полосе (Um J₁; Um J₂; Um J₃; Um J₄).

Еще одной важной особенностью спектра ЧМ сигнала является то, что можно добиться отсутствия составляющей несущего сигнала или сделать ее амплитуду значительно меньше амплитуд информационных составляющих без дополнительных технических усложнений модулятора. Для этого необходимо подобрать такой индекс модуляции Мчм, при котором J₀(Мчм) будет равно нулю (в месте пересечения функции J₀ с осью Мчм), например Мчм=2,4.

Достоинством частотной модуляции являются:

Основным недостатком данной модуляции является большая ширина спектра модулированного сигнала.

Частотная модуляция используется:

Фазовая модуляция

Фазовая модуляция — процесс изменения фазы несущего сигнала в соответствии с мгновенными значениями модулирующего сигнала.

Рассмотрим математическую модель фазо-модулированного (ФМ) сигнала при гармоническом модулирующем сигнале. При воздействии модулирующего сигнала

на несущее колебание

происходит изменение мгновенной фазы несущего сигнала по закону:

где а_фм — коэффициент пропорциональности частотной модуляции.

Подставляя ?фм(t) в S(t) получаем математическую модель ФМ сигнала при гармоническом модулирующем сигнале:

Произведение а_фм Um_u=Dj_m называется индексом фазовой модуляции или девиацией фазы.

Поскольку изменение фазы вызывает изменение частоты, то используя (11) определяем закон изменения частоты ФМ сигнала:

Произведение а_фмUm_u?=??_m является девиацией частоты фазовой модуляции. Сравнивая девиацию частоты при частотной и фазовой модуляциях можно сделать вывод, что и при ЧМ и при ФМ девиация частоты зависит от коэффициента пропорциональности и амплитуды модулирующего сигнала, но при ФМ девиация частоты также зависит и от частоты модулирующего сигнала.

Временные диаграммы поясняющие процесс формирования ФМ сигнала приведены на рисунке 10.

Ширина спектра ФМ сигнала определяется выражением:

Достоинствами фазовой модуляции являются:

Дискретная двоичная модуляция (манипуляция гармонической несущей)

Дискретная двоичная модуляция (манипуляция) — частный случай аналоговой модуляции, при которой в качестве несущего сигнала используется гармоническая несущая, а в качестве модулирующего сигнала используется дискретный, двоичный сигнал.

Различают четыре вида манипуляции:

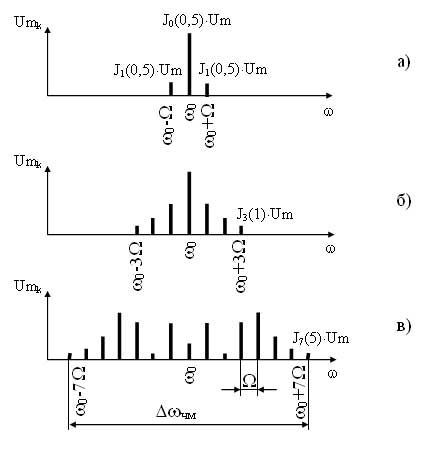
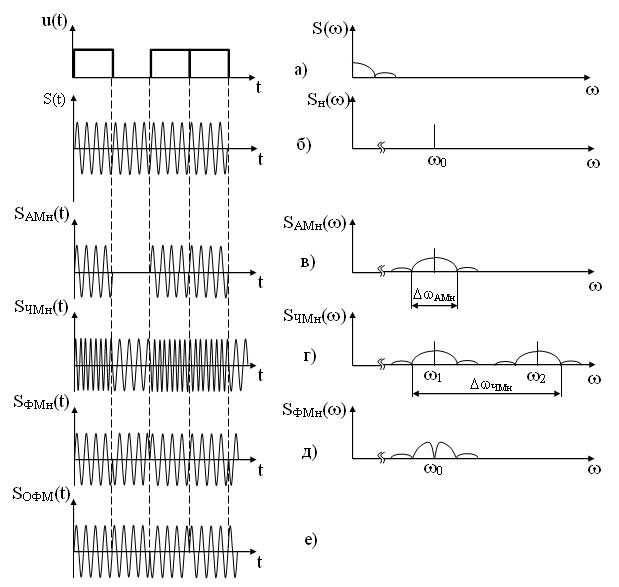
Временные и спектральные диаграммы модулированных сигналов при различных видах манипуляции представлены на рисунке 11.

При амплитудной манипуляции, также как и при любом другом модулирующем сигнале огибающая S_АМн(t) повторяет форму модулирующего сигнала (рисунок 11, в).

При фазовой манипуляции фаза несущего сигнала изменяется на 180° в момент изменения амплитуды модулирующего сигнала. Если следует серия из нескольких импульсов, то фаза несущего сигнала на этом интервале не изменяется (рисунок 11, д).

При относительно-фазовой манипуляции фаза несущего сигнала изменяется на 180° лишь в момент подачи импульса, т. е. при переходе от активной паузы к посылке (0?1) или от посылке к посылке (1?1). При уменьшении амплитуды модулирующего сигнала фаза несущего сигнала не изменяется (рисунок 11, е). Спектры сигналов при ФМн и ОФМн имеют одинаковый вид (рисунок 9, е).

Сравнивая спектры всех модулированных сигналов можно отметить, что наибольшую ширину имеет спектр ЧМн сигнала, наименьшую — АМн, ФМн, ОФМн, но в спектрах ФМн и ОФМн сигналов отсутствует составляющая несущего сигнала.

В виду большей помехоустойчивости наибольшее распространение получили частотная, фазовая и относительно-фазовая манипуляции. Различные их виды используются в телеграфии, при передаче данных, в системах подвижной радиосвязи (телефонной, транкинговой, пейджинговой).

Импульсная модуляция

Импульсная модуляция — это модуляция, при которой в качестве несущего сигнала используется периодическая последовательность импульсов, а в качестве модулирующего может использоваться аналоговый или дискретный сигнал.

Поскольку периодическая последовательность характеризуется четырьмя информационными параметрами (амплитудой, частотой, фазой и длительностью импульса), то различают четыре основных вида импульсной модуляции:

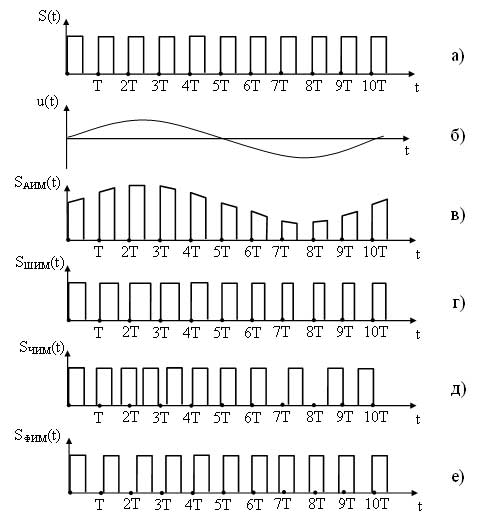
Временные диаграммы импульсно-модулированных сигналов представлены на рисунке 12.

При АИМ происходит изменение амплитуды несущего сигнала S(t) в соответствии с мгновенными значениями модулирующего сигнала u(t), т. е. огибающая импульсов повторяет форму модулирующего сигнала (рисунок 12, в).

При ШИМ происходит изменение длительности импульсов S(t) в соответствии с мгновенными значениями u(t) (рисунок 12, г).

При ЧИМ происходит изменение периода, а соответственно и частоты, несущего сигнала S(t) в соответствии с мгновенными значениями u(t) (рисунок 12, д).

При ФИМ происходит смещение импульсов несущего сигнала относительно их тактового (временного) положения в немодулированной несущей (тактовые моменты обозначены на диаграммах точками Т, 2Т, 3Т и т. д.). ФИМ сигнал представлен на рисунке 12, е.

Поскольку при импульсной модуляции переносчиком сообщения является периодическая последовательность импульсов, то спектр импульсно-модулированных сигналов является дискретным и содержит множество спектральных составляющих. Этот спектр представляет собой спектр периодической последовательности импульсов в котором возле каждой гармонической составляющей несущего сигнала находятся составляющие модулирующего сигнала (рисунок 13). Структура боковых полос возле каждой составляющей несущего сигнала зависит от вида модуляции.

Также важной особенностью спектра импульсно-модулированных сигналов является то, что ширина спектра модулированного сигнала, кроме ШИМ, не зависит от модулирующего сигнала. Она полностью определяется длительностью импульса несущего сигнала. Поскольку при ШИМ длительность импульса изменяется и зависит от модулирующего сигнала, то при этом виде модуляции и ширина спектра также зависти от модулирующего сигнала.

Частоту следования импульсов несущего сигнала может быть определена по теореме В. А. Котельникова как f₀ =2Fmax. При этом Fmax это верхняя частота спектра модулирующего сигнала.

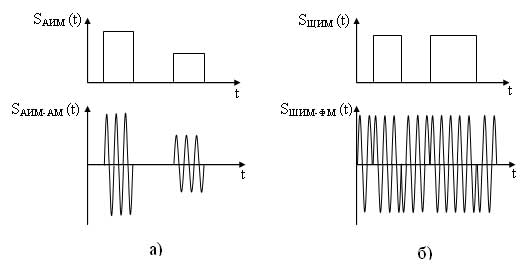
Передача импульсно модулированных сигналов по высокочастотным линиям связи невозможна, т. к. спектр этих сигналов содержит низкочастотные составляющий. Поэтому для передачи осуществляют повторную модуляцию. Это модуляция, при которой в качестве модулирующего сигнала используют импульсно-модулированный сигнал, а в качестве несущего гармоническое колебание. При повторной модуляции спектр импульсно-модулированного сигнала переносится в область несущей частоты. Для повторной модуляции может использоваться любой из видов аналоговой модуляции: АМ, ЧС, ФМ. Полученная модуляция обозначается двумя аббревиатурами: первая указывает на вид импульсной модуляции а вторая — на вид аналоговой модуляции, например АИМ-АМ (рисунок 14, а) или ШИМ-ФМ (рисунок 14, б) и т. д.

Источник

Виды сигналов, модуляция

Аналоговая величина – величина, значения которой в заданном интервале изменяются непрерывно. Её конкретное значение зависит только от точности прибора, производящего измерения. Это, например, температура.

Дискретная величина – величина, значения которой изменяются скачкообразно. Например, число студентов в аудитории. Измерительный сигнал – сигнал, содержащий количественную информацию об измеряемой физической величине. Например, напряжение на выходе термоэлектрического преобразователя, измеряющего температуру.

Сигнал данных – форма представления сообщения данных с помощью физической величины, изменения одного или нескольких параметров которой, отображает его изменение.

В микропроцессорной технике сигналами являются электрические величины (ток, напряжение). Представляющий параметр сигнала данных – параметр сигнала данных, изменение которого отображает изменение сообщения данных (амплитуда, частота, фаза, длительность импульса, длительность паузы).

Аналоговый сигнал данных – сигнал данных, у которого каждый из представляющих параметров описывается функцией времени и непрерывным множеством возможных значений, т.е. аналоговые сигналы описываются непрерывной (или кусочно-непрерывной) функцией x_a(t), причём сама функция и аргумент t могут принимать любые значения на некоторых интервалах

Аналоговый сигнал f (t) называется периодическим, если существует действительное число T, такое, что f (t + T) = f (t) для любых t, при этом T называется периодом сигнала.

Сама функция x_д (nT) может в дискретные моменты принимать произвольные значения на некотором интервале. Эти значения функции называются выборками или отсчётами функции. Другим обозначением решётчатой функции x(nT) является x(n) или xn. Последовательность x(n) может быть конечной или бесконечной, в зависимости от интервала определения функции.

Квантованный сигнал данных – отличается от аналоговых или дискретных разбиением диапазона значений непрерывной или дискретной величины на конечное число интервалов. Простейшим видом квантования является деление целочисленного значения на натуральное число, называемое коэффициентом квантования.

Цифровой сигнал данных – сигнал, у которого каждый из представляющих параметров описывается функцией дискретного времени и конечным множеством возможных значений. Цифровые сигналы описываются квантованными решётчатыми функциями x_ц(nT). При получении цифрового сигнала из аналогового происходят дискретизация и квантование.

Двоичный цифровой сигнал – сигнал данных, в котором используется способ представления информации о величине параметра в виде многоразрядной комбинации двух величин – нуля и единицы – и называемый обычно двоичным кодом.

В двоичном коде используются только две цифры: 1 и 0. Любое число содержит некоторое количество разрядов, в каждом из которых может стоять только одна из этих цифр. Одна цифра соответствует одному состоянию какого-либо элемента, например, замкнутому контакту, а другая — другому состоянию элемента — разомкнутому контакту.

Модуляция – процесс изменения одного или нескольких параметров высокочастотного несущего колебания по закону низкочастотного информационного сигнала (сообщения).

В наше время двоичные цифровые сигналы в связи с простотой кодирования и обработки используются в цифровых электронных устройствах. Для передачи цифрового сигнала по каналам связи (например, электрическим или радиоканалам) используются различные виды модуляции.

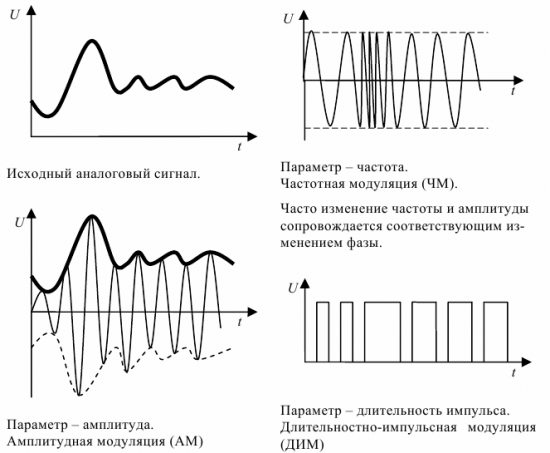
Рассмотрим примеры представляющих параметров сигналов данных на примере различных видов модуляции (см. рис. 1). Кроме рассмотренных видов модуляции, также существуют фазовая (ФМ), время-импульсная (ВИМ), широтно-импульсная (ШИМ) и другие модуляции.

Рис. 1. Различные виды модуляции сигналов – различные представляющие параметры сигналов данных

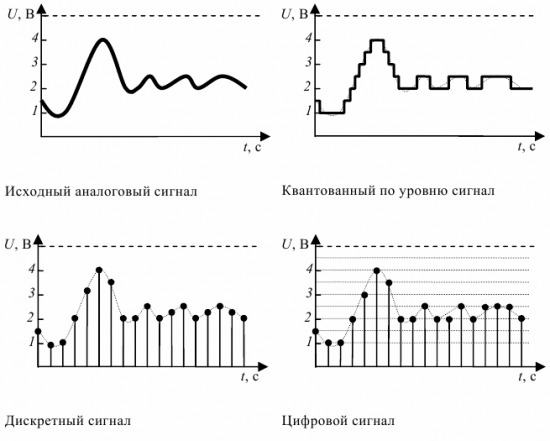
Для понимания сущности цифрового сигнала рассмотрим следующую классификацию. В цифровой технике выделяют сигналы (рис. 2):

произвольные по величине и непрерывные во времени (аналоговые);

произвольные по величине и дискретные по времени (дискретные);

квантованные по величине и непрерывные по времени (квантованные);

квантованные по величине и дискретные по времени (цифровые).

Рис. 2. Аналоговый, дискретный, квантованный и цифровой сигналы

Аналоговые сигналы часто используют для представления непрерывно изменяющихся физических величин. Например, аналоговый электрический сигнал, снимаемый с термопары, несёт информацию об изменении температуры, сигнал с микрофона – о быстрых изменениях давления в звуковой волне и т.п.

В области цифровой и импульсной техники терминология не является установившейся. Так, дискретный сигнал – это сигнал, значения представляющего параметра которого известны только в определённые моменты времени, а также это сигнал, в отличие от аналогового, представляющий параметр которого может принимать только фиксированные значения (обычно два: логический «ноль» или логическую «единицу»).

Во втором случае было бы правильно называть сигнал квантованным, но промышленные модули называются «модулями ввода дискретных сигналов». Кроме использования для передачи информации различных физических величин, сигналы различаются также представляющими параметрами.

Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!

Подписывайтесь на наш канал в Telegram!

Просто пройдите по ссылке и подключитесь к каналу.

Не пропустите обновления, подпишитесь на наши соцсети:

Источник