какие виды потерь рассматривает уравнение бернулли
Уравнение Бернулли
Уравнение Бернулли для струйки жидкости формулируется следующим образом: для элементарной струйки идеальной жидкости полная удельная энергия, т.е. сумма удельной энергии положения, удельной энергии давления и кинетической удельной энергии – есть величина постоянная во всех сечениях струйки.
Уравнение Бернулли выглядит так:
Подробное описание всех входящих в состав уравнения параметров уже описан в этой статье.
Содержание статьи
Смысл уравнения Бернулли
По существу вывода уравнение Бернулли для струйки идеальной жидкости представляет собой закон сохранения механической энергии, составленный применительно к единице массового расхода жидкости. Это следует из того, что в процессе вывода значения работы сил, приложенных к выделенному объему струйки и значения кинетической энергии этого объема были поделены на величину ρqΔT.
Отсюда вытекает, что поскольку член υ 2 /2 является мерой кинетической энергии единицы массы движущейся жидкости, то сумма членов gz+p/ρ будет мерилом ее потенциальной энергии.
В отношении величины gz это очевидно, ведь если частица жидкости массы m расположена на высоте z относительно некоторой плоскости и находится под действием сил тяжести, то способность ее совершить работу, т.е. её потенциальная энергия относительно этой плоскости равняется mgz. Но если её поделить на массу частиц m, то эта часть потенциальной энергии даст величину gz.
Для более ясного физического представления о том, что потенциальная энергия измеряется величиной p/ρ рассмотрим такую схему: пусть к трубе, заполненной жидкостью с избыточным давлением p, присоединен пьезометр, снабженный на входе в него краном.
Кран сначала закрыт, т.е. пьезометр свободен от жидкости, а элементарный объем жидкости ΔV массой ρ*ΔV перед краном находится под давлением p.
Если затем открыть кран, то жидкость в пьезометре поднимется на некоторую высоту, равную
Таким образом, единица массы, находящейся под давлением p, как бы несет в себе ещё заряд потенциальной энергии, определяемой величиной p/ρ.
В гидравлике для характеристики удельной энергии обычно используется понятие напор, под которым понимают энергию жидкости, отнесенную к единице силы тяжести, а не её массы. В соответствии с этим уравнение Бернулли записанное в начале этой статьи примет вид
Такое уравнение Бернулли для элементарной струйки идеальной жидкости в другой форме, весьма удобно для гидравлических расчетов и может быть сформулировано следующим образом.
Для элементарной струйки идеальной жидкости полный напор, т.е. сумма геометрического, пьезометрического и скоростного напоров, есть величина постоянная во всех её сечениях.
Отсюда следует, что между напором и удельной энергией существует очень простая зависимость
где э – удельная энергия
Уравнение Бернулли для элементарной струйки реальной жидкости
Если вместо идеальной жидкости рассматривать жидкость реальную, то уравнение Бернулли для реальной жидкости должно принять несколько другой вид.
При движении идеальной жидкости её полная удельная энергия или напор сохраняет постоянное значение по длине струйки, а при движении реальной жидкости эта энергия будет убывать по направлению движения. Причиной этого являются затраты энергии на преодоление сопротивлений движению, обусловленные внутренним трением в вязкой жидкости.
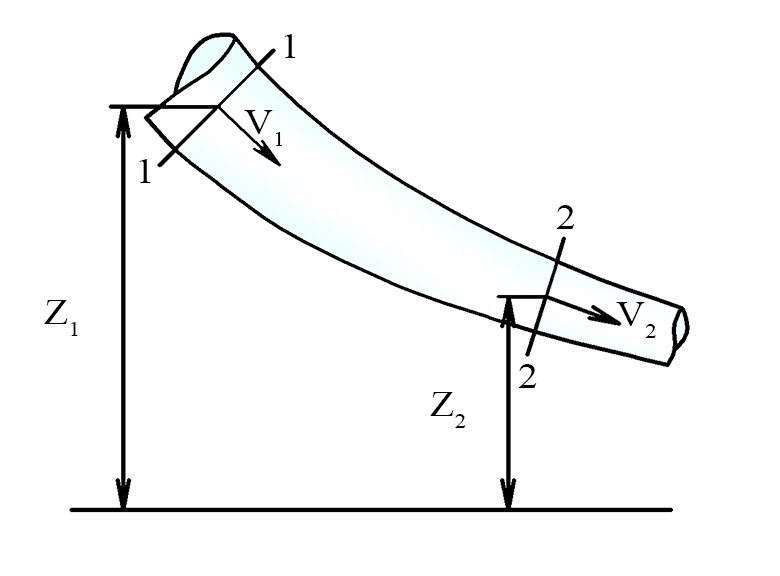
Если же мы рассмотрим два сечения для струйки идеальной жидкости: 1-1 в начале и 2-2 в конце струйки, то полная удельная энергия будет
Полная удельная энергия для сечения 1-1 всегда будет больше, чем полная удельная энергия для сечения 2-2 на некоторую величину потерь, и уравнение Бернулли в этом случае получается
Величина Э1-2 представляет собой меру энергии, потерянную единицей массы жидкости на преодоление сопротивлений при её движениями между указанными сечениями.
Уравнение Бернулли для потока реальной жидкости
Уравнение Бернулли для струйки реальной жидкости это еще только половина дела, ведь в при решении различных практических вопросов о движении жидкостей приходится иметь дело с потоками конечных размеров. Уравнение Бернулли в этом случае может быть получено, исходя из рассмотрения потока как совокупности множества элементарных струек.
Учитывая, что все струйки движутся с одной и той же средней скоростью форма записи уравнения Бернулли для потока идеальной жидкости становится идентичной его записи для элементарной струйки.
В таком виде уравнение Бернулли обычно и применяется при решении практических задач для потоков однородной несжимаемой жидкости при установившемся движении, происходящем под действием одной силы тяжести.
Такое уравнение составляется для различных живых сечений потока, вблизи которых движение жидкости должно удовлетворять условиям медленно изменяющегося движения, хотя на пути между этими сечениями движение может и не удовлетворять указанным условиям.
Поэтому полная потеря напора между двумя сечениями потока при наличии сопротивлений обоих видов будет
Видео по теме
Уравнение Бернулли подходит и для газов. Явление уменьшения давления при повышении скорости потока является основой работы различных приборов для измерения расхода. Закон Бернулли справедлив и для жидкостей вязкость которых равна нулю. При описании течения таких жидкостей используют уравнение Бернулли с добавлением слагаемых учитывающих потери на местные сопротивления.
Уравнение Бернулли
Уравнение Бернулли для потока идеальной жидкости
Запишем для этого случая уравнение, связывающее между собой скорость движения жидкости и ее давление в каждом сечении.
Указанное уравнение называют законом или уравнением Бернулли для элементарной струйки идеальной несжимаемой жидкости.
Уравнение Бернулли можно записать и в другом виде, умножим обе части уравнения на g получим:
Физический смысл уравнения Бернулли
Составляющие уравнения Бернулли являются различными формами удельной (отнесенной к единице массы) механической энергии жидкости:
Физический и энергетический смысл уравнения Бернулли заключается в постоянстве полной удельной энергии вдоль элементарной струйки идеальной жидкости.
Уравнение Бернулли отражает закон сохранения механической энергии для идеальной несжимаемой жидкости.
Уравнение Бернулли для потока реальной вязкой жидкости
Если на участке между расчетными сечениями не совершается механическая работа, а движение является установившимся, без притока и отбора жидкости, и сама жидкость является несжимаемой, то для потока будут справедливы зависимости:
Иллюстрация уравнения Бернулли
Для иллюстрации закона Бернулли на координатной плоскости, совмещенной с принципиальной гидравлической схемой системы изображают напорную и пьезометрическую линии.
Уравнение Бернулли для горизонтальной трубы
Для горизонтальных трубопроводов и силовых гидроприоводов, в которых пьезометрический набор существенно превышает геометрический удобна следующая форма записи уравнения Бернулли:
Алгоритм решения задач с помощью уравнения Бернулли
Задачи с помощью уровнения Бернулли удобно решать в следующей последовательности:
3.2. Уравнение д. Бернулли с учетом потерь энергии
При установившемся, плавно изменяющемся движении потока реальной жидкости уравнение Бернулли для двух сечений будет иметь следующий вид:
,
где V1 иV2– средние скорости движения в сечениях;
– коэффициент кинетической энергии, принимаемый при турбулентном режиме движения равным 1,0—1,1, а при ламинарном
= 2 (в круглой трубе);
– потери удельной энергии на преодоление сил сопротивления движению потока на участке между сечениями. Различают два вида потерь энергии: по длине и на преодоление местных сопротивлений. В общем случае:
,
где h1 — потери энергии по длине;
— сумма потерь энергии на преодоление местных сопротивлений. Оба вида потерь энергии определяются по такой зависимости:
,
где 
— коэффициент потерь.
При учете потерь энергии по длине в трубопроводах, коэффициент потерь определяется так:
где 
— гидравлический коэффициент трения (коэффициент Дарси);l— длина участка трубопровода, на котором определяются потери энергии;
d — диаметр трубопровода.
При ламинарном режиме движения коэффициент трения зависит только от числа Рейнольдса и для труб круглого сечения определяется по формуле
При турбулентном режиме могут быть выделены три области гидравлических сопротивлений.
Область гладких русел для труб при числах Рейнольдса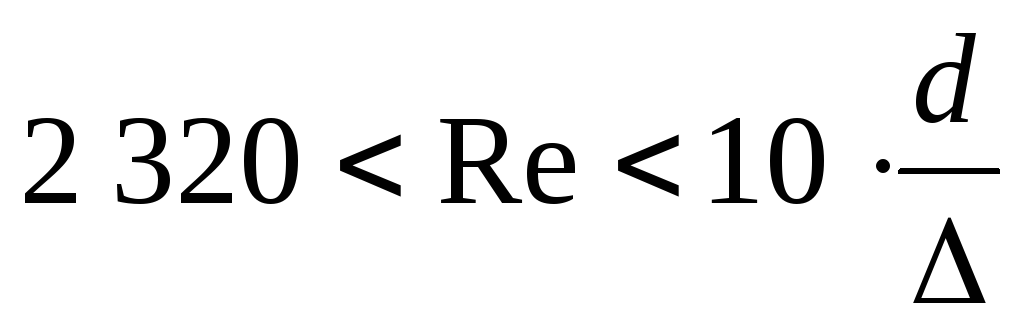
,
где 
— диаметр трубопровода;
— эквивалентная шероховатость.
В этой области гидравлических сопротивлений коэффициент трения 
зависит только от числа Рейнольдса и может быть определен по формуле Блазиуса
.
Переходная область наблюдается при числах Рейнольдса
В этом случае для определения коэффициента трения может быть рекомендована формула А. Д. Альтшуля:
.
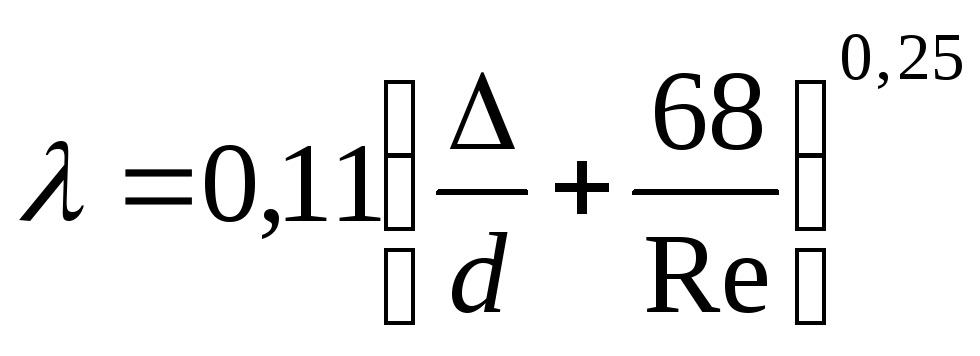
Как видно из этой зависимости, в переходной области гидравлических сопротивлений коэффициент трения зависит и от числа Рейнольдса и от шероховатости трубы.
Квадратичная область гидравлических сопротивлений наступает при
. В этой области коэффициент трения не зависит от числа Рейнольдса и может быть определен по формуле Шифринсона:
.
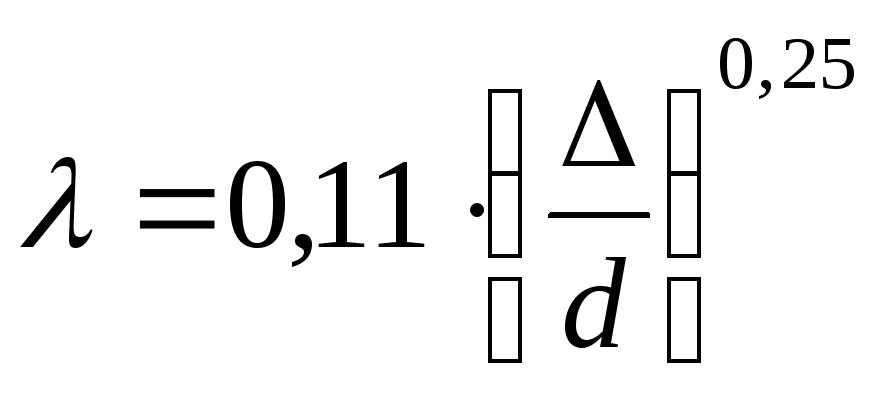
В этой же области гидравлических сопротивлений для стальных и чугунных труб, бывших в употреблении, может быть рекомендована формула Ф. А. Шевелева:
.
Для определения границ областей гидравлических сопротивлений может быть использован следующий график:
Рис. 3.1. График зон гидравлического сопротивления
Величина эквивалентной шероховатости 
зависит от материала, способа изготовления и соединения труб, от продолжительности эксплуатации. Ниже приводятся значения эквивалентной шероховатости для некоторых труб(мм):
Новые стальные цельнотянутые трубы
Новые чугунные трубы
Стальные водопроводные, находившиеся в эксплуатации
Коэффициенты потерь 
местных сопротивлений зависят от вида сопротивлений:
= 0,5 — вход в трубу при острых входных кромках;
= 6 — вход в трубу с сеткой;
= 10 — вход в трубу с сеткой и обратным клапаном;
= 1 — выход из трубы под уровень жидкости;
= 4 — прохождение воды через вентильd = 0,1м при его полном открытии;
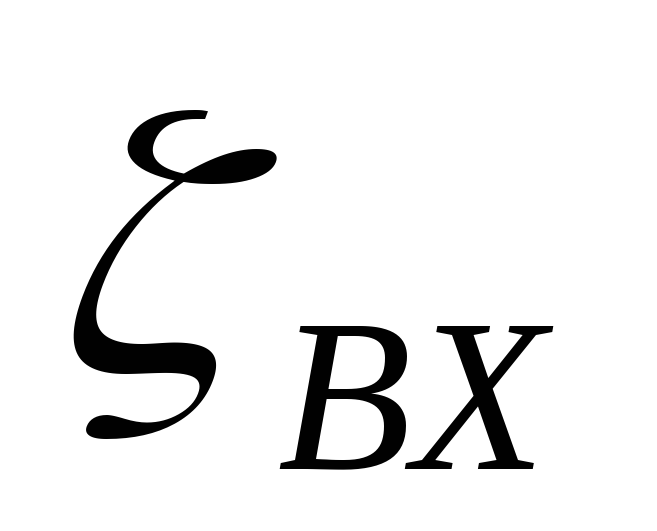
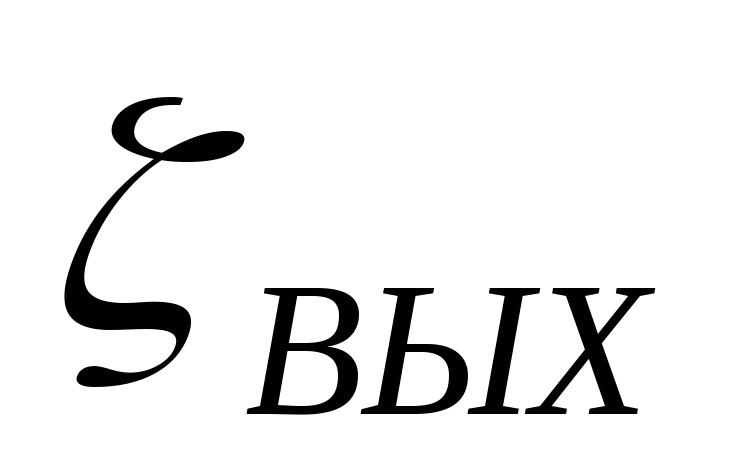
Коэффициенты потерь при внезапном расширении и внезапном сужении трубопровода приведены в таблицах П-17 и П-18 приложения.
Потери энергии на внезапное расширение и внезапное сужение трубопроводов определяются по скорости за сопротивлением.
При наличии местных сопротивлений, а также сопротивлений по длине общая потеря энергии определяется суммированием потерь энергии, обусловленных различными сопротивлениями
Уравнение Бернулли. Потери напора.
Движение жидкости в трубопроводах и каналах осуществляется за счет энергии самой жидкости. Механическая энергия жидкости состоит из трех видов: энергии положения, энергии давления и кинетической энергии. В гидравлике широко используют понятие напора. Под напором понимают энергию жидкости отнесенную к единице веса (см. пункт 3.2).
Полный гидродинамический напор движущейся жидкости H (полная удельная энергия) равен сумме геометрического напора z (удельная потенциальная энергия положения), пьезометрического напора 
(удельная потенциальная энергия давления) и скоростного напора 
(удельная кинетическая энергия):
,
Геометрический напор равен расстоянию от плоскости сравнения до рассматриваемой точки жидкости (для потока жидкости – до точки, совпадающей с центром тяжести рассматриваемого сечения).
Пьезометрический напор характеризует запас энергии жидкости, обусловленный ее давлением относительно давления сравнения (часто атмосферного давления).
Геометрический и пьезометрический напоры присущи и жидкости находящейся в покое, поэтому их сумму называют гидростатическим напором.
Скоростной напор характеризует запас энергии обусловленный скоростью ее движения.
В потоке идеальной жидкости, движущейся по трубопроводам и каналам, вследствие отсутствия потерь энергии при движении, полный гидродинамический напор жидкости остается постоянным. Это условие является частным случаем закона сохранения энергии. Записанное для двух сечений потока жидкости равенство полных гидродинамических напоров называют уравнением Даниила Бернулли по имени его автора. Это уравнение является основным уравнением гидродинамики.
,
Оно может быть записано и как 
.
При движении реальной вязкой жидкости вследствие влияния сил молекулярного сцепления между стенкой и жидкостью происходит торможение потока, приводящее к скольжению слоев жидкости друг относительно друга и возникновению напряжений трения между слоями. Кроме того, движение вязкой жидкости часто сопровождается вращением частиц, вихреобразованием и перемешиванием. Все это требует затрат энергии жидкости, поэтому энергия реальной жидкости не остается постоянной, как в случае идеальной жидкости, а постепенно расходуется на преодоление сопротивлений и, следовательно, уменьшается вдоль потока.
В соответствии со сказанным уравнение Бернулли для реальной жидкости имеет следующий вид:
,
В результате полная удельная энергия жидкости в сечении 1-1 будет больше полной удельной энергии в сечении 2-2 на величину потерянной удельной энергии 
(рисунок 21).
Потерянная удельная энергия или потерянный напор обозначаются 
и имеют также линейную размерность [8,11].
Общие потери напора на участке трубопровода 
равны сумме потерь напора по длине и потерь напора на местные сопротивлении.х
.
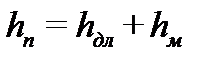
Основной расчетной формулой для потерь напора по длине при ламинарном и турбулентном режиме движения жидкости в круглых трубах является формула Вейсбаха-Дарси и имеющая следующий вид:
,
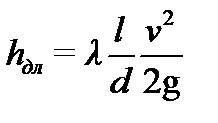
где λ– коэффициент гидравлического трения (иначе его называют коэффициент потерь на трение или коэффициент трения);
d – диаметр трубопровода, м;
– средняя скорость движения жидкости, м/с;
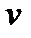
Коэффициент трения при ламинарном режиме движения жидкости рассчитывается по формуле:
,
На практике при турбулентном режиме движения коэффициент трения может быть определен по графику Г.А. Мурина (рисунок 24) или рассчитан по формуле А.Д. Альтшуля:
,
где Re – критерий Рейнольдса,
– коэффициент трения;
–значение абсолютной шероховатости, м.
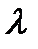
d – диаметр трубопровода, м.
Для гидравлически гладких труб шероховатость на сопротивление не влияет, и коэффициент трения однозначно определяется числом Re по формуле Блазиуса:
,
Потери напора на местном сопротивлении рассчитываются в долях от величины скоростного напора:
,
где ξ – коэффициент местного сопротивления,
– скорость движения жидкости, м/с;
Величину ξ для каждого вида местного сопротивления определяют по справочным данным, для некоторых местных сопротивлений имеются расчетные формулы 4.
Общие потери напора в трубопроводе (сумма потерь по длине и на местных сопротивлениях) рассчитываются:
= 
,
где 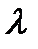– коэффициент трения;
– длина трубопровода, м;
d – диаметр трубопровода, м.
– скорость движения жидкости, м/с;
– сумма коэффициентов местных сопротивлений.
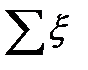
На практике при движение жидкостей чаще необходимо определять не потери напора, а потери давления 
. С учетом того, что 
потери давления по длине (на трение) будут равны:
.
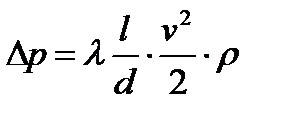
Общие потери давления: 
.
Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого.
Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим.