какие виды уравнений бывают
Виды уравнений и методы их решения
В разработке рассматриваются виды алгебраических уравнений и методы их решения.
Просмотр содержимого документа
«Виды уравнений и методы их решения»
Виды уравнений и методы их решения
Уравнения подразделяются на две большие группы: алгебраические и трансцендентные. Алгебраическим называется такое уравнение, в котором для нахождения корня уравнения используются только алгебраические действия, а именно четыре арифметических – сложение, вычитание, умножение и деление, а также возведение в степень и извлечение натурального корня. Трансцендентным называется уравнение, в котором для нахождения корня используются не алгебраические функции: например, тригонометрические, логарифмические и иные.
В курсе математики основной школы рассматриваются только алгебраические уравнения. Рассмотрим более подробно их виды и алгоритм решения.
Группу алгебраических уравнений можно условно разделить на такие виды уравнений как:
целые — с обеими частями, состоящими из целых алгебраических выражений по отношению к неизвестным;
дробные — содержащие целые алгебраические выражения в числителе и знаменателе;
иррациональные — алгебраические выражения здесь находятся под знаком корня.
Дробные и иррациональные уравнения можно свести к решению целых уравнений.
Рассмотрим особенности решения алгебраических уравнений
В алгебре рассматриваются два вида равенств – тождества и уравнения.
Остановимся на основных понятиях.
В общем виде уравнение может быть записано так:
F (
В зависимости от числа неизвестных уравнение называют уравнением с одним, двумя и т. д. неизвестными.
Значение неизвестных, обращающие уравнение в тождество (верное равенство), называют решениями уравнения.
Решить уравнение – это значит найти множество его решений или доказать, что решений нет. В зависимости от вида уравнения множество решений уравнения может быть бесконечным, конечным и пустым.
Если все решения одного уравнения являются решениями другого уравнения, то такие уравнения называют эквивалентными.
Рассмотрим некоторые эквивалентные уравнения:
Уравнение 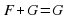
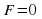
Уравнение 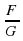
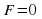
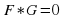
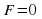
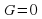
Уравнение 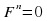
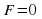
Уравнение 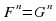
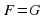
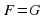
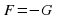
Алгебраическим уравнением называется уравнение вида 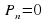
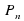
Алгебраическим уравнением с одним неизвестным называется уравнение, сводящееся к уравнению вида:
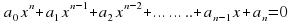
Главная задача при решении любого уравнения – свести его к простейшим.
Все ниже перечисленные уравнения имеют так же и свое графическое решение, которое заключается в том, чтобы представить левую и правую части уравнения как две одинаковые функции от неизвестного. Затем строится график сначала одной функции, а затем другой и точка (и) пересечения двух графиков даст решение (я) исходного уравнения. Примеры графического решения всех уравнений даны в приложении.
Рассмотрим методы решения уравнений.
Линейным уравнением называется уравнение первой степени.
где a и b – некоторые действительные числа.
Алгебраическое уравнение второй степени (3),
где a, b, с– некоторые действительные числа, называется квадратным уравнением.
Корни квадратного уравнения вычисляются по формуле
Выражение называется дискриминантом квадратного уравнения.
Частными видами квадратного уравнения (3) являются:
1) Приведенное квадратное уравнение (в случае, если ), которое обычно записывается в виде
Корни приведенного квадратного уравнения вычисляются по формуле
Эту формулу называют формулой Виета – по имени французского математика конца XVI в., внесшего значительный вклад в становление алгебраической символики.
2) Квадратное уравнение с четным вторым коэффициентом, которое обычно записывается в виде
Корни этого квадратного уравнения удобно вычислять по формуле
Формулы (4) и (5) являются частными видами формулы для вычисления корней полного квадратного уравнения.
Корни приведенного квадратного уравнения
связаны с его коэффициентами Формулами Виета
В случае, если приведенное квадратное уравнение имеет действительные корни, формулы Виета позволяют судить как о знаках, так и об относительной величине корней квадратного уравнения, а именно:
Перепишем еще раз квадратное уравнение
и покажем еще один способ как можно вывести корни квадратного уравнения (6) через его коэффициенты и свободный член. Если
то корни квадратного уравнения вычисляются по формуле
которая может быть получена в результате следующих преобразований исходного уравнения, а так же с учетом формулы (7).
Уравнения n-й степени вида
называется двучленным уравнением. При и заменой (2))
которое и будет далее рассматриваться.
Двучленное уравнение при четном n имеет действительный корней не имеет. В множестве комплексных чисел уравнение имеет корней, вычисляемых по формуле (10).
Приведем краткую сводку множеств корней двучленного уравнения для некоторых конкретных значений n.
Уравнение имеет один дествительный корень и два комплексных корня
Уравнение имеет один дествительный корень и два комплексных корня
Уравнение действительных корней не имеет. Комплексные корни:
Если квадратные уравнения умели решать еще математики Вавилонии и Древней Индии, то кубические, т.е. уравнения вида
оказались “крепким орешком”. В конце XV в. профессор математики в университетах Рима и Милана Лука Пачоли в своем знаменитом учебнике “Сумма знаний по арифметике, геометрии, отношениям и пропорциональности” задачу о нахождении общего метода для решения кубических уравнений ставил в один ряд с задачей о квадратуре круга. И все же усилиями итальянских алгебраистов такой метод вскоре был найден.
Начнем с упрощения
Если кубическое уравнение общего вида
Так же как в основе решения квадратного уравнения лежит формула квадрата суммы, решение кубического уравнения опирается на формулу куба суммы:
Чтобы не путаться в коэффициентах, заменим здесь на и перегруппируем слагаемые:
Итак, мы показали, что в кубическом уравнении (11) с помощью подходящей подстановки можно избавиться от члена, содержащего квадрат неизвестного. Поэтому теперь будем решать уравнение вида
Давайте еще раз обратимся к формуле куба суммы, но запишем ее иначе:
Сравните эту запись с уравнением (13) и попробуйте установить связь между ними. Даже с подсказкой это непросто. Надо отдать должное математикам эпохи Возрождения, решившим кубическое уравнение, не владея буквенной символикой. Подставим в нашу формулу :
Теперь уже ясно: для того, чтобы найти корень уравнения (13), достаточно решить систему уравнений
Эта формула известная как формула Кардано.
подстановкой приводится к “неполному” виду
Пусть “неполное” кубичное уравнение (14) действительно.
а) Если (“неприводимый” случай), то и
Во всех случаях берется действительное значение кубичного корня.
Алгебраическое уравнение четвертой степени.
Уравнения четвертой степени
Метод решения уравнений четвертой степени нашел в XVI в. Лудовико Феррари, ученик Джероламо Кардано. Он так и называется – метод Феррари.
Как и при решении кубического и квадратного уравнений, в уравнении четвертой степени
а само уравнение сводится к двум квадратным:
Их корни и дают все решения исходного уравнения.
Решим для примера уравнение
Здесь удобнее будет воспользоваться не готовыми формулами, а самой идеей решения. Перепишем уравнение в виде
Теперь приравняем к нулю дискриминант правой части уравнения:
или, после упрощения,
подстановкой приводится к “неполному” виду
в которых сочетания знаков выбираются так, чтобы удовлетворялось условие
Уравнения высоких степеней
Разрешимость в радикалах
Формула корней квадратного уравнения известна с незапамятных времен, а в XVI в. итальянские алгебраисты решили в радикалах уравнения третьей и четвертой степеней. Таким образом, было установлено, что корни любого уравнения не выше четвертой степени выражаются через коэффициенты уравнения формулой, в которой используются только четыре арифметические операции (сложение, вычитание, умножение, деление) и извлечение корней степени, не превышающей степень уравнения. Более того, все уравнения данной степени ( ) можно “обслужить” одной общей формулой. При подстановке в нее коэффициентов уравнения получим все корни – и действительные, и комплексные.
После этого естественно возник вопрос: а есть ли похожие общие формулы для решения уравнений пятой степени и выше? Ответ на него смог найти норвежский математик Нильс Хенрик Абель в начале XIX в. Чуть раньше этот результат был указан, но недостаточно обоснован итальянцем Паоло Руффини. Теорема Абеля-Руффини звучит так:
Общее уравнение степени при неразрешимо в радикалах.
с целыми коэффициентами, можно выразить в радикалах через рациональные числа. На самом деле такое выражение существует далеко не всегда. Это следует из теоремы разрешимости алгебраических уравнений, построенной выдающимся французским математиком Эваристом Галуа в его “Мемуаре об условиях разрешимости уравнений в радикалах” (1832 г.; опубликован в 1846 г.).
Подчеркнем, что в прикладных задачах нас интересует только приближенные значения корней уравнения. Поэтому его разрешимость в радикалах здесь обычно роли не играет. Имеются специальные вычислительные методы, позволяющие найти корни любого уравнения с любой наперед заданной точностью, ничуть не меньшей, чем дают вычисления по готовым формулам.
Уравнения, которые решаются
Хотят уравнения высоких степеней в общем случае неразрешимы в радикалах, да и формулы Кардано и Феррари для уравнений третьей и четвертой степеней в школе не проходят, в учебниках по алгебре, на вступительных экзаменах в институты иногда встречаются задачи, где требуется решить уравнения выше второй степени. Обычно их специально подбирают так, чтобы корни уравнений можно было найти с помощью некоторых элементарных приемов.
В основе одного из таких приемов лежит теорема о рациональных корнях многочлена:
С помощью этой теоремы можно найти все рациональные корни уравнения с целыми коэффициентами испытанием конечного числа “кандидатов”. Например, для уравнения
Если один корень найден, можно понизить степень уравнения. Согласно теореме Безу,
Из теоремы непосредственно следует, что
Продолжая наш пример, вынесем из многочлена
Решение простых линейных уравнений
Понятие уравнения
Понятие уравнения обычно проходят в самом начале школьного курса алгебры. Его определяют, как равенство с неизвестным числом, которое нужно найти.
В школьной программе за 7 класс впервые появляется понятие переменных. Их принято обозначать латинскими буквами, которые принимают разные значения. Исходя из этого можно дать более полное определение уравнению.
Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Значение неизвестных нужно найти так, чтобы при их подстановке в пример получилось верное числовое равенство.
Например, возьмем выражение 2 + 4 = 6. При вычислении левой части получается верное числовое равенство, то есть 6 = 6.
Уравнением можно назвать выражение 2 + x = 6, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.
Корень уравнения — то самое число, которое при подстановке на место неизвестной уравнивает выражения справа и слева.
Равносильные уравнения — это те, в которых совпадают множества решений. Другими словами, у них одни и те же корни.
Решить уравнение значит найти все возможные корни или убедиться, что их нет.
Решить уравнение с двумя, тремя и более переменными — это два, три и более значения переменных, которые обращают данное выражение в верное числовое равенство.
Какие бывают виды уравнений
Уравнения могут быть разными, самые часто встречающиеся — линейные и квадратные.
Особенность преобразований алгебраических уравнений в том, что в левой части должен остаться многочлен от неизвестных, а в правой — нуль.


