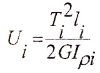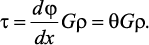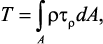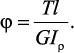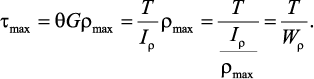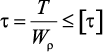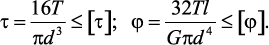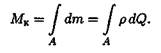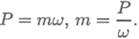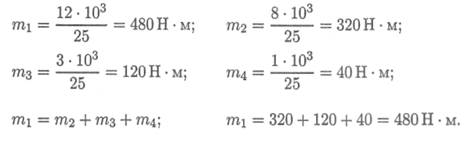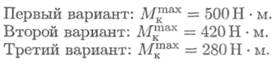какие внутренние усилия возникают при кручении

Тема 2.4. Кручение

Под кручением понимается такой вид деформации, когда в поперечных сечениях бруса действует только крутящий момент M_k, (другое обозначение T, M_z), а остальные силовые факторы (нормальная и поперечная силы и изгибающие моменты) отсутствуют.

Или другое определение кручением называют деформацию, возникающую при действии на стержень пары сил, расположенной в плоскости, перпендикулярной к его оси (рис.1).

Кручение возникает в валах, винтовых пружинах, в элементах пространственных конструкций и т.п.

Деформация кручения наблюдается если прямой брус нагружен внешними моментами (парами сил M), плоскости действия которых перпендикулярны к его продольной оси

В чистом виде деформация кручения встречается редко, обычно присутствуют и другие внутренние силовые факторы (изгибающие моменты, продольные силы).

Стержни круглого или кольцевого сечения, работающие на кручение, называют валами.

Внешние крутящие моменты передаются на вал в местах посадки на него шкивов, зубчатых колес, там, где поперечная нагрузка смещена относительно оси вала.

Мы будем рассматривать прямой брус только в состоянии покоя или равномерного вращения. В этом случае алгебраическая сумма всех внешних скручивающих моментов, приложенных к брусу, будет равна нулю.

При расчете брусьев, испытывающий деформацию кручения, на прочность и жесткость при статическом действии нагрузки, надо решить две основные задачи. Это определение напряжений (от M_k), возникающих в брусе, и нахождение угловых перемещений в зависимости от внешних скручивающих моментов.

При расчете валов обычно бывает известна мощность, передаваемая на вал, а величины внешних скручивающих моментов, подлежат определению. Внешние скручивающие моменты, как правило, передаются на вал в местах посадки на него шкивов, зубчатых колес и т.п.

§2. Построение эпюр крутящих моментов

Для определения напряжений и деформаций вала необходимо знать значения внутренних крутящих моментов M_k (M_z) в поперечных сечениях по длине вала. Диаграмму, показывающую распределение значений крутящих моментов по длине бруса, называют эпюрой крутящих моментов. Зная величины внешних скручивающих моментов и используя метод сечений, мы можем определить крутящие моменты, возникающие в поперечных сечениях вала.

В простейшем случае, когда вал нагружен только двумя внешними моментами (эти моменты из условия равновесия вала ΣM_z=0 всегда равны друг другу по величине и направлены в противоположные стороны), как показано на рис. 1, крутящий момент M_z в любом поперечном сечении вала (на участке между внешними моментами) по величине равен внешнему моменту |M₁|=|M₂|.

Источник

iSopromat.ru

Кручением называется такой вид деформации бруса, при котором в его поперечных сечениях возникает только один внутренний силовой фактор – крутящий момент T.

Брусья, испытывающие кручение, принято называть валами.

Внутренний крутящий момент

Внутренние скручивающие моменты появляются под действием внешних крутящих моментов m_i, расположенных в плоскостях, перпендикулярных к продольной оси бруса.

Скручивающие моменты передаются на вал в местах посадки зубчатых колес, шкивов ременных передач и т.п.

Величина крутящего момента в любом сечении вала определяется методом сечений: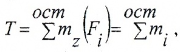

т.е. крутящий момент численно равен алгебраической сумме скручивающих моментов m_i, расположенных по одну сторону от рассматриваемого сечения.

Правило знаков внутренних скручивающих моментов:
Положительными принимаются внутренние моменты, стремящиеся повернуть рассматриваемую часть вала против хода часовой стрелки, при рассмотрении со стороны отброшенной части вала.

В технике наиболее широко используются валы круглого поперечного сечения.

Теория кручения круглых валов основана на следующих гипотезах:

Напряжения при кручении

В поперечных сечениях вала при кручении имеют место только касательные напряжения.
Касательные напряжения, направленные перпендикулярно к радиусам, для произвольной точки, отстоящей на расстоянии ρ от центра, вычисляются по формуле: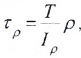

где I_ρ — полярный момент инерции.
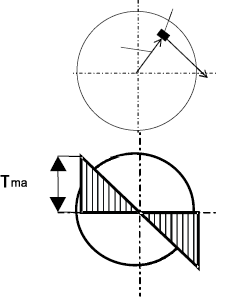
Эпюра касательных напряжений при кручении имеет следующий вид: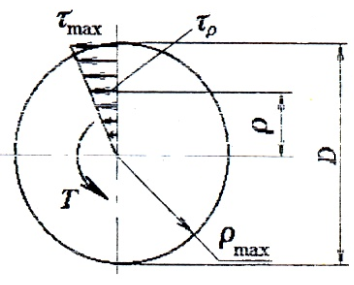

Касательные напряжения меняются по линейному закону и достигают максимального значения на контуре сечения при ρ= ρ_max: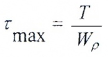

Здесь: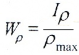

— полярный момент сопротивления.
Геометрические характеристики сечений:
а) для полого вала: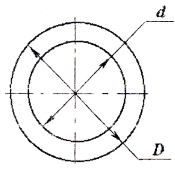


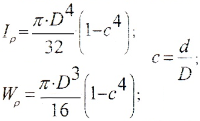
б) для вала сплошного сечения (c=0)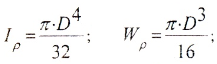

в) для тонкостенной трубы (t 0,9)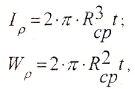

где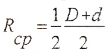

— радиус срединной поверхности трубы.

Деформации

Деформации валов при кручении заключаются в повороте одного сечения относительно другого.

Угол закручивания вала на длине Z определяется по формуле: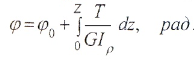

Если крутящий момент и величина GI_ρ, называемая жесткостью поперечного сечения при кручении, постоянны, для участка вала длиной l имеем: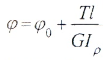

Угол закручивания, приходящийся на единицу длины, называют относительным углом закручивания: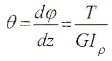

Расчет валов сводится к одновременному выполнению двух условий:

Для стальных валов принимается:

Используя условия прочности и жесткости, как и при растяжении – сжатии можно решать три типа задач:

Из двух найденных значений крутящего момента необходимо принять меньшее.

Потенциальная энергия упругой деформации определяется по формуле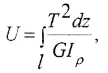

или для участка вала при постоянном T и GI_ρ

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Источник

Научная электронная библиотека

Лекция 7. КРУЧЕНИЕ

Крутящие моменты (внутренний силовой фактор) в поперечных сечениях стержня. Кручение стержней круглого поперечного сечения: допущения, деформации, напряжения, углы закручивания. Условия прочности, жёсткости. Построение эпюр крутящих моментов.

Кручение имеет место в случае действия на вал момента (пары сил) относительно его продольной оси, и в поперечных сечениях бруса возникает только один силовой фактор – крутящий момент. Брус, работающей на кручение называется валом. При кручении вала его поперечные сечения поворачиваются друг относительно друга, вращаясь вокруг оси бруса.

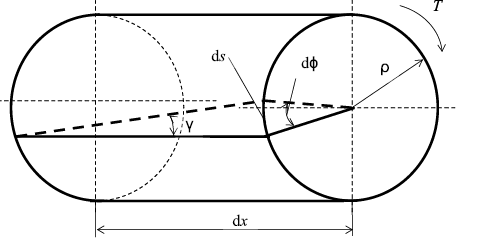
Напряжения и деформации при кручении бруса. Под действием внешнего скручивающего момента, приложенного на правом конце бруса, левый конец которого жестко закреплен, брус будет закручиваться. Выделим из бруса элементарный цилиндр длиной dx (рис. 19). Будем считать, что левое сечение бруса жестко закреплено. Под действием крутящего момента T правое сечение повернется на некоторый угол dφ.Так как ds = γ•dx = ρ•dφ, то получаем 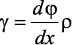. Из данной зависимости видно, что угол сдвига γ изменяется по радиусу вала по линейному закону.

Рис. 19. Расчетная схема при кручении

Деформация бруса при кручении характеризуется относительным углом закручивания .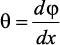

При малых углах закручивания вала в теории кручения круглых стержней принимаются допущения:

1. Поперечные сечения, плоские и перпендикулярные к его оси до деформации, остаются плоскими (не коробятся) и перпендикулярными к оси вала и после деформации (гипотеза Бернулли).

2. Радиусы поперечных сечений при деформации не искривляются и не изменяют своей длины.

3. Длина вала в результате закручивания не изменяется.

Поперечное сечение вала ведет себя при кручении, как жесткий диск, и деформацию кручения можно рассматривать, как результатсдвига одного поперечного сечения относительно другого. В этом случае в точках поперечного сечения вала возникают только касательные напряжения.

Теория кручения, основанная на упомянутых допущениях, подтверждается экспериментальными данными.

Согласно закону Гука при сдвиге, имеем 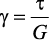. Откуда получаем:

Из полученной зависимости следует, что касательные напряжения изменяются по радиусу по линейному закону.

При кручении все внутренние силы, распределенные по поперечному сечению, приводятся к одной составляющей – к крутящему моменту. Касательные напряжения перпендикулярны радиусам, проведенные через точки их действия (рис. 20). Крутящий момент T в сечении бруса определяется по формуле

где ρ – плечо элементарной силы.

Подставляя значение касательного ускорения, получим

(8)

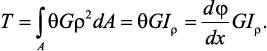
Элементарный угол закручивания бруса: 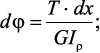полный угол закручивания

Максимальное касательное напряжение в поперечном сечении бруса будет определяться по зависимости:

Прочность и жесткость при кручении. Условие прочности при кручении имеет вид

(9)

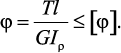
Для бруса круглого сечения эти условия принимают вид:

Построение эпюр крутящих моментов. Крутящий момент, возникающий в поперечном сечении стержня, определяется методом сечений. Крутящий момент равен алгебраической сумме скручивающих моментов, приложенных к любой из частей стержня. Эпюра крутящих моментов – это график, показывающий изменения крутящего момента по длине вала. Правило знаков для эпюры крутящих моментов

При построении эпюры крутящих моментов используется правило знаков: скручивающий момент, вращающий рассматриваемую часть стержня против хода часовой стрелки при взгляде на поперечное сечение, вызывает в этом сечении положительный крутящий момент.

Брус разбивается на участке, на каждом участке проводится сечение и определяется крутящий момент. Затем строится эпюра крутящих моментов.

Источник

Деформация кручения

В различных механизмах детали подвергаются влиянию разных сил, приводящих к возникновению деформаций. Далее рассмотрена деформация кручения: факторы и закономерности ее проявления, формирующие ее силы, особенности деформации изделий различной формы.

Основные понятия

Под кручением понимают вид деформации, свойственный для условий приложения к телу силы в поперечной плоскости. В результате этого в поперечном разрезе формируется крутящий момент. Деформациям кручения подвергаются валы и пружины.

Валом называют функционирующую на кручение вращающуюся деталь в виде стержня.

Под торсионом понимают функционирующий на кручение стержень, применяемый в качестве упругого элемента.

Для круглых валов, наиболее обширно применяемых в технике, разработана теория кручения. Она основана на трех положениях:

Из приведенных положений следует, что кручение представлено деформацией сдвига материала между соседними поперечными сечениями, обусловленной проворотом последних вокруг оси.

Деформациями при кручении считают взаимный проворот сечений. Они формируются вследствие воздействия на стержень пар сил с перпендикулярными к его продольной оси плоскостями действия.

Величина деформаций описывается углом закручивания. Под полным понимают угол поворота свободного конца. Относительным считают значение для определенной длины вала. Данные параметры рассчитывают с учетом прочности и жесткости деталей.

Угол закручивания стержня цилиндрической конфигурации в границах упругих деформаций определяется уравнением закона Гука для кручения, представляющего отношение произведения момента и длины вала к произведению геометрического полярного инерционного момента и модуля сдвига.

Относительный угол закручивания вычисляют как частное угла закручивания и длины стержня.

Под вращающими либо скручивающими моментами понимают показатели пар сил, воздействующих на вал. Их подразделяют на внешние, называемые вращающими и скручивающими, и внутренние (крутящие). Под влиянием перпендикулярных продольной оси бруса внешних крутящих моментов формируются внутренние. Они передаются на деталь в точках установки шкивов ременных передач, зубчатых колес и т. д.

Крутящий момент представлен силовым фактором, обуславливающим круговое передвижение сечения относительно перпендикулярной ему оси или препятствующим ему. Его значение равно сумме скручивающих усилий по одну сторону от данной точки. Положительными считают внутренние моменты, направленные против часовой стрелки со стороны внешней нормали (отброшенной части). При этом соответствующий внешний момент имеет направление, совпадающее с ходом часовой стрелки.

Условия прочности и жесткости применяют для решения следующих задач:

Под эпюрой крутящих моментов понимают график, отображающий закон их изменения по длине либо сечению детали.

При разделении детали по длине на три участка в соответствии с методом сечений получится, что для первого (правого) фрагмента наблюдается линейная зависимость крутящего момента от координаты сечения ввиду влияния равномерно распределенной нагрузки, для второго и третьего участков данная зависимость отсутствует. При этом в точках приложения внешних сосредоточенных усилий наблюдаются скачки, соответствующие их величине.

В сечении наблюдается линейное изменение, определяемое законом касательных напряжений, в прямой зависимости от расстояния от центра.

Таким образом, в продольном разрезе наибольшие деформации кручения характерны для точки, наиболее удаленной от места закрепления детали. В поперечном разрезе максимальные деформации кручения наблюдаются на поверхности.

Полярный инерционный момент сечения представляет собой геометрическую характеристику жесткости при кручении для круглого вала. Полярный момент сопротивления сечения является аналогичным параметром для его прочности.

Следует отметить, что большинство приведенных выше понятий описывается с применением формул.

Напряжения кручения

Исходя из приведенного выше определения деформации кручения, при данном процессе в поперечном сечении наблюдаются лишь касательные напряжения, направленные перпендикулярно к радиусам. Их определяют для конкретной точки как произведение соотношения крутящего момента к геометрическому полярному инерционному моменту и расстояния данной точки от оси кручения.

Изменение касательных напряжения линейно, и максимальной величины они достигают на поверхности при наибольших значениях крутящего момента и расстояния от оси кручения, поэтому ее значение вычисляют как частное наибольшего крутящего и полярного моментов сопротивления.

С применением данного условия возможно вычислить прочие параметры: по силовым факторам, создающим крутящий момент – показатель сопротивления и далее размеры сечения в зависимости от формы, либо по размеру сечения – максимально допустимое для него значение крутящего момента и на основе последней допустимые значения внешних нагрузок.

Касательные напряжения, по закону парности, формируются при кручении как в поперечных, так и в продольном направлениях. Вследствие этого во всех точках вала наблюдается деформация в виде чистого сдвига. Главные напряжения направлены к образующей под углом 45°.

Помимо скручивающих усилий возможно воздействие на вал моментной нагрузки.

Из изложенных выше данных следует, что удаление материала в районе оси вала незначительно сказывается на прочности ввиду того, что данная часть мало нагружена. При равных площади сечения и массе деталей кольцевые варианты характеризуются большими полярными моментами сопротивления и инерции по сравнению со сплошными валами. То есть при равной массе полые варианты прочнее и жестче, а при одинаковых показателях прочности и жесткости легче. Названные параметры определяют устойчивость данных изделий к деформации.

Выше были рассмотрены особенности деформации кручения круглых в поперечном разрезе предметов. Для треугольных, прямоугольных, эллиптических и прочих вариантов не применима гипотеза плоских сечений. Это обусловлено тем, что поверхности данного типа при кручении искривляются. Данный процесс их коробления вследствие смещения отдельных точек при деформации вдоль оси называют депланацией. Вследствие этого методы сопротивления материалов для вычисления кручений и напряжений неприменимы. Вместо них используют методы теории упругости.

Для изделий произвольной поперечной формы касательные напряжения имеют направление по касательной к контуру, однако при наличии внешних углов они отсутствуют. Так, при разложении напряжения вблизи угла по нормалям к его сторонам надвое из закона парности следует формирование касательных напряжений на свободной поверхности. Однако в данном случае она свободна от нагрузки, поэтому у внешнего угла касательные напряжения обнуляются.

Для наиболее распространенных среди вариантов некруглого сечения прямоугольных валов наибольшие напряжения характерны для поверхностных участков в середине длинных сторон. Следовательно, там наблюдается наибольшая деформация кручения.

Прямоугольные детали в сравнении с круглым характеризуются значительно меньшими жесткостью и прочностью. Причем это отличие увеличивается с ростом отношения сторон. Следовательно, они более подвержены деформации.

Источник

Внутренние силовые факторы при кручении.

Построение эпюр крутящих моментов

Иметь представление о деформациях при кручении, о внутрен­них силовых факторах при кручении.

Уметь строить эпюры крутящих моментов.

Деформации при кручении

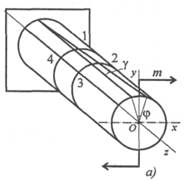
Кручение круглого бруса происходит при нагружении его па­рами сил с моментами в плоскостях, перпендикулярных продольной оси. При этом образующие бруса искривляются и разворачиваются на угол γ называемый углом сдвига (угол поворота образующей). Поперечные сечения разворачиваются на угол φ, называемый углом закручивания (угол поворота сечения, рис. 26.1).

Длина бруса и размеры поперечного сечения при кручении не изменяются.

Тема 2.5. Кручение. Внутренние силовые факторы при кручении 217

Связь между угловыми деформациями определяется соотноше­нием

l— длина бруса; R — радиус сечения.

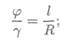
Длина бруса значительно больше радиуса сечения, следователь­но, φ » γ.

Угловые деформации при кручении рассчитываются в радиа­нах.

Гипотезы при кручении

1. Выполняется гипотеза плоских сечений: поперечное сечение бруса, плоское и перпендикулярное продольной оси, после деформа­ции остается плоским и перпендикулярным продольной оси.

2. Радиус, проведенный из центра поперечного сечения бруса, после деформации остается прямой линией (не искривляется).

3. Расстояние между поперечными сечениями после деформации не меняется. Ось бруса не искривляется, диаметры поперечных се­чений не меняются.

Внутренние силовые факторы при кручении

Кручением называется нагружение, при котором в поперечном сечении бруса возникает только один внутренний силовой фактор — крутящий момент.

Внешними нагрузками также являются две противоположно на­правленные пары сил.

Рассмотрим внутренние силовые факторы при кручении круг­лого бруса (рис. 26.1).

Для этого рассечем брус плоскостью I и рассмотрим равновесие отсеченной части (рис. 26.1а). Сечение рассматриваем со стороны отброшенной части.

Внешний момент пары сил разворачивает участок бруса про­тив часовой стрелки, внутренние силы упругости сопротивляются повороту. В каждой точке сечения возникает поперечная сила dQ (рис. 26.16). Каждая точка сечения имеет симметричную, где возни­кает поперечная сила, направленная в обратную сторону. Эти силы образуют пару с моментом dm = pdQ; p — расстояние от точки

С помощью интегрирования получим суммарный момент сил упругости, называемый крутящим моментом:

Практически крутящий момент определяется из условия равно­весия отсеченной части бруса.

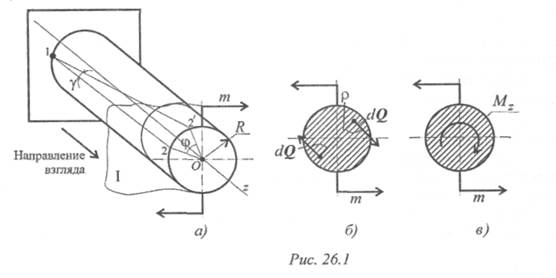
Крутящий момент в сечении равен сумме моментов внешних сил, действующих на отсеченную часть (рис. 26.1в):

Эпюры крутящих моментов

Крутящие моменты могут меняться вдоль оси бруса. После определения величин моментов по сечениям строим график-эпюру крутящих моментов вдоль оси бруса.

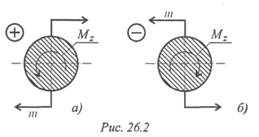
Крутящий момент считаем положительным, если моменты внешних пар сил направлены по часовой стрелке, в этом случае мо­мент внутренних сил упругости направлен против часовой стрелки (рис. 26.2).

Порядок построения эпюры моментов аналоги­чен построению эпюр про­дольных сил. Ось эпюры параллельна оси бруса, значения моментов откла­дывают от оси вверх или вниз, масштаб построе­ния выдерживать обязательно.

Примеры решения задач

Тема 2.5. Кручение. Внутренние силовые факторы при кручении 219

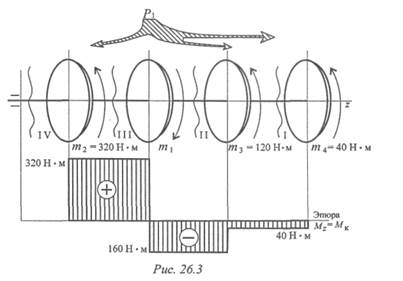
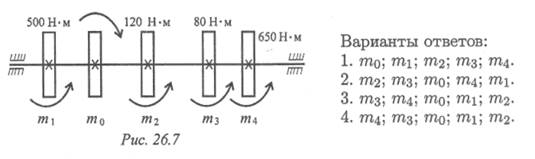
вал вращается с постоянной скоростью ώ = 25 рад/с. Построить эпюру крутящих моментов на валу.

Решение

1. Определяем моменты пар сил на шкивах. Вращающий момент определяем из формулы мощности при вра­щательном движении

Момент на шкиве1 движущий, а моменты на шкивах 2, 3, 4 — моменты сопротивления механизмов, поэтому они имеют противо­положное направление. Брус скручивается между движущим момен­том и моментами сопротивления. При равновесии момент движущий равен сумме моментов сопротивления:

2. Определяем крутящие моменты в поперечных сечениях бруса
с помощью метода сечений.

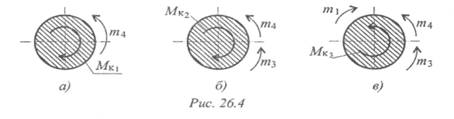
Сечение I (рис. 26.4а):

Сечение II (рис. 26.4b):

– m4 – т₃ + М_К2 = 0; М_К2 = m4 + m3; М_К2 = 40 + 120 = 160Н•м — крутящий момент отрицательный.

Сечение III (рис. 26.4в):

3. Строим эпюру крутящих моментов. Заметим, что скачок на
эпюре всегда численно равен приложенному вращающему моменту.

Выбираем соответствующий масштаб.

Откладываем значения моментов, штрихуем эпюру поперек, об­водим по контуру, записываем значения моментов (см. эпюру под схемой вала (рис. 26.3)). Максимальный крутящий момент на участ­ке IIIМкз =320Н•м.

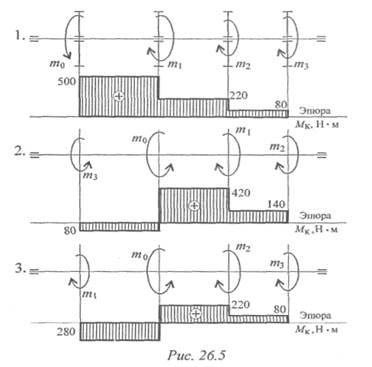
Пример 2.Выбрать рациональное расположение колес на валу (рис. 26.5). т1= 280 Н • м; т₂ = 140 Н • м; т₃ = 80 Н • м.

Примечание. Меняя местами колеса (шкивы) на валу, можно изменять величины крутящих моментов. Рациональным рас­положением является такое, при котором крутящие моменты принимают минимальные из возможных значения.

Тема 2.5. Кручение. Внутренние силовые факторы при кручении 221

Рассмотрим нагрузки на валу при различном расположении колес.

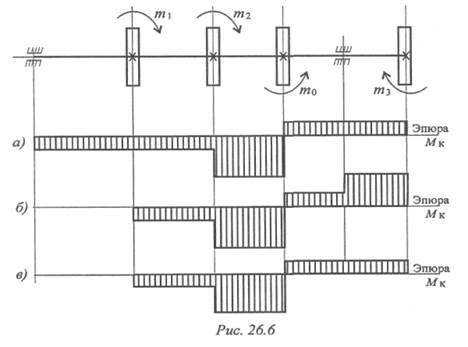
Из представленных вариантов наиболее рационально располо­жение шкивов в третьем случае, здесь значения крутящих момен­тов минимальны. Вывод: при установке шкивов желательно, чтобы мощность подавалась в середине вала и по возможности равномерно распределялась направо и налево.

Контрольные вопросы и задания

1. Какие деформации возникают при кручении?

2. Какие гипотезы выполняются при деформации кручения?

3. Изменяются ли длина и диаметр вала после скручивания?

4. Какие внутренние силовые факторы возникают при кручении?

5. Что такое рациональное расположение колес на валу?

6. Для заданного вала (рис. 26.6) выбрать соответствующую
эпюру крутящих моментов (а, б, в). m1 = 40Н•м; т2 = 180Н•м;
m₀ = 280Н•м.

7. В каком порядке рациональнее расположить шкивы на валу
для уменьшения нагрузки на вал (рис. 26.7)?

Тема 2.5. Кручение 223

Тема 2.5. Кручение.

Напряжения и деформации

При кручении

Иметь представление о напряжении и деформациях при круче­нии, о моменте сопротивления при кручении.

Знать формулы для расчета напряжений в точке поперечного сечения, закон Гука при кручении.

Напряжения при кручении

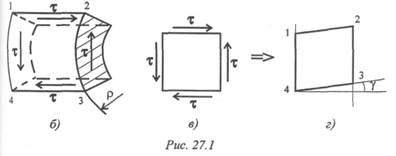
Проводим на поверхности бру­са сетку из продольных и попе­речных линий и рассмотрим рису­нок, образовавшийся на поверхно­сти после деформации (рис. 27.1а). Поперечные окружности, оставаясь плоскими, поворачиваются на угол φ, продольные линии искривляют­ся, прямоугольники превращают­ся в параллелограммы. Рассмотрим элемент бруса 1234 после деформа­ции.

При выводе формул используем закон Гука при сдвиге и гипотезу

плоских сечений и неискривления радиусов поперечных сечений.

При кручении возникает напряженное состояние, называемое «чистый сдвиг» (рис. 27.16).

При сдвиге на боковой поверхности элемента 1234 возникают касательные напряжения, равные по величине (рис. 27.1в), элемент деформируется (рис. 27.1г).

Материал подчиняется закону Гука. Касательное напряжение пропорционально углу сдвига.

Закон Гука при сдвиге τ = Gγ,

Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций.

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого.

Источник