какие волны могут интерферировать

Интерференция волн

Интерференция волн — взаимное увеличение или уменьшение результирующей амплитуды двух или нескольких когерентных волн, одновременно распространяющихся в пространстве. [1] Сопровождается чередованием максимумов и минимумов (пучностей) интенсивности в пространстве. Результат интерференции (интерференционная картина) зависит от разности фаз накладывающихся волн.

Интерферировать могут все волны, однако устойчивая интерференционная картина будет наблюдаться только в том случае, если волны имеют одинаковую частоту и колебания в них не ортогональны. Интерференция может быть стационарной и нестационарной. Стационарную интерференционную картину могут давать только полностью когерентные волны. Например, две сферические волны на поверхности воды, распространяющиеся от двух когерентных точечных источников, при интерференции дадут результирующую волну, фронтом которой будет сфера.

При интерференции энергия волн перераспределяется в пространстве. [1] Это не противоречит закону сохранения энергии потому, что в среднем, для большой области пространства, энергия результирующей волны равна сумме энергий интерферирующих волн. [2]

При наложении некогерентных волн средняя величина квадрата амплитуды (то есть интенсивность результирующей волны) равна сумме квадратов амплитуд (интенсивностей) накладывающихся волн. Энергия результирующих колебаний каждой точки среды равна сумме энергий её колебаний, обусловленных всеми некогерентными волнами в отдельности. Именно отличие результирующей интенсивности волнового процесса от суммы интенсивностей его составляющих и есть признак интерференции. [3]

Содержание

Расчет результата сложения двух сферических волн

Если в некоторой однородной и изотропной среде два точечных источника возбуждают сферические волны, то в произвольной точке пространства M может происходить наложение волн в соответствии с принципом суперпозиции (наложения): каждая точка среды, куда приходят две или несколько волн, принимает участие в колебаниях, вызванных каждой волной в отдельности. Таким образом волны не взаимодействуют друг с другом и распространяются независимо друг от друга.

Две одновременно распространяющиеся синусоидальные сферические волны и , созданные точечными источниками B₁ и B₂, вызовут в точке M колебание, которое, по принципу суперпозиции, описывается формулой . Согласно формуле сферической волны:

, ,

и — фазы распространяющихся волн и — волновые числа () и — циклические частоты каждой волны и — начальные фазы, и — расстояния от точки М до точечных источников B₁ и B₂

В результирующей волне , амплитуда и фаза определяются формулами:

,

Когерентность волн

Волны и возбуждающие их источники называются когерентными, если разность фаз волн не зависит от времени. Волны и возбуждающие их источники называются некогерентными, если разность фаз волн изменяется с течением времени. Формула для разности:

, где , ,

— скорость распространения волны, одинаковая для обеих волн в данной среде. В приведенном выше выражении от времени зависит только первый член. Две синусоидальные волны когерентны, если их частоты одинаковы (), и некогерентны, если их частоты различны.

Для когерентных волн () при условии

, .

Амплитуда результирующих колебаний в любой точке среды не зависит от времени. Косинус равен единице, а амплитуда колебаний в результирующей волне максимальна во всех точках среды, для которых , где (m-целое) или , (так как )

Величина называется геометрической разностью хода волн от их источников B₁ и B₂, до рассматриваемой точки среды.

Амплитуда колебаний в результирующей волне минимальна во всех точках среды, для которых

, где (m-натуральное),

.

При наложении когерентных волн квадрат амплитуды и энергия результирующей волны отличны от суммы квадратов амплитуд и суммы энергий накладываемых волн.

См. также

Примечания

Литература

Ссылки

Интерференция волн — на поверхности воды, возбуждаемых в двух точках. ИНТЕРФЕРЕНЦИЯ ВОЛН (от латинского inter, здесь взаимно и fero несу), взаимное усиление или ослабление двух или нескольких волн при их наложении друг на друга при одновременном распространении в… … Иллюстрированный энциклопедический словарь

ИНТЕРФЕРЕНЦИЯ ВОЛН — явление, наблюдающееся при одновременном распространении в пространстве нескольких волн и состоящее в стационарном (или медленно изменяющемся) пространственном распределении амплитуды и фазы результирующей волны. Интерференция волн возможна, если … Большой Энциклопедический словарь

интерференция волн — 1. Явление, состоящее в ослаблении или усилении амплитуд колебаний при сложении двух и большего числа волн одинаковой частоты в зависимости от соотношения их фаз. 2. Явление, состоящее в возникновении максимумов и минимумов звукового давления при … Справочник технического переводчика

ИНТЕРФЕРЕНЦИЯ ВОЛН — ИНТЕРФЕРЕНЦИЯ ВОЛН, явление, при котором две волны одинаковой длины и в общем случае имеющие один источник, распространяясь не в одном направлении, взаимодействуют в некоторой точке. Когда ФАЗЫ этих волн связаны постоянным отношением т. е. если… … Научно-технический энциклопедический словарь

интерференция волн — сложение в пространстве двух (или нескольких) волн, в результате чего происходит ослабление или усиление амплитуды результирующей волны. Интерференция волн возникает при наличии когерентности (определённой корреляции фаз) налагающихся волн.… … Энциклопедический словарь

ИНТЕРФЕРЕНЦИЯ ВОЛН — явление, возникающее при наложении двух или неск. волн и состоящее в устойчивом во времени их взаимном усилении в одних точках пространства и ослаблении в др. в зависимости от соотношения между фазами этих волн (см. рис.). Интерферировать могут… … Большой энциклопедический политехнический словарь

ИНТЕРФЕРЕНЦИЯ ВОЛН — сложение в про странстве двух (или неск.) волн, в результате чего происходит ослабление или усиление амплитуды результирующей волны. И. в. возникает при наличии когерентности (определ. корреляции фаз) налагающихся волн. Интерференция характерна… … Естествознание. Энциклопедический словарь

интерференция волн — bangų interferencija statusas T sritis fizika atitikmenys: angl. wave interference vok. Welleninterferenz, f rus. интерференция волн, f pranc. interférence d’ondes, f … Fizikos terminų žodynas

Интерференция волн — (лат. взаимно, между собой ударяю, поражаю) взаимное усиление или ослабление двух (или большего числа) волн при их наложении друг на друга при одновременном распространении в пространстве. Обычно под интерференционным эффектом понимается отличие… … Концепции современного естествознания. Словарь основных терминов

Источник

Интерференция световых волн

Интерференция – это одно из наиболее ярких проявлений волновой природы света. Мы можем наблюдать такое интересное и красивое явление, если наложить друг на друга 2 или более световых пучков. В месте перекрывания пучков интенсивность волны света обладает характером чередующихся светлых и темных полос, при этом в точках максимумов интенсивность больше, а в точках минимумов меньше суммы интенсивностей пучков.

При белом свете интерференционные полосы окрашиваются в разные цвета светового спектра. На практике интерференционные явления окружают нас повсюду. Это и цвета масляных пятен на асфальте, и окрашивание замерзающих оконных стекол, и чудесные цветные рисунки на крыльях отдельных бабочек и жуков.

Первый научный эксперимент проявления интерференции света

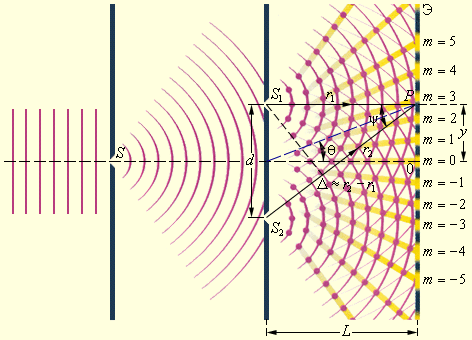
Интерференционный опыт Юнга

Путем простых тригонометрических вычислений можно прийти к следующему выражению для интенсивности результирующего колебания в точке P :

где Δ = r 2 – r 1 – это разность хода.

Подчеркнем, что в волновой оптике понятие “луч света” теряет физический смысл в отличие от геометрической оптики. Определение «луч» в волновой оптике употребляется для краткости обозначения направления распространения волны.

Далее данный термин будет упоминаться без кавычек.

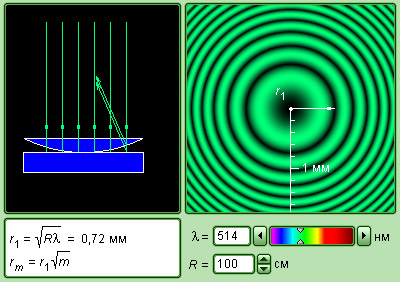
По данной формуле рассчитывается длина световой волны λ при известном радиусе кривизны R линзы.

Проблема когерентности волн

Источник

Какие волны могут интерферировать

Любому волновому движению присущи явления интерференции и дифракции, с которыми мы начинаем сейчас знакомиться.
Для того чтобы убедиться в том, что свет имеет волновую природу, необходимо было найти экспериментальные доказательства интерференции и дифракции света.

Чтобы лучше понять явление интерференции света, мы вначале остановимся на интерференции механических волн.

Сложение волн

Очень часто в среде одновременно распространяется несколько различных волн.
Например, когда в комнате беседуют несколько человек, то звуковые волны накладываются друг на друга.
Что при этом происходит?

Проще всего проследить за наложением механических волн, наблюдая волны на поверхности воды.
Если мы бросим в воду два камня, образовав тем самым две круговые волны, то можно будет заметить, что каждая волна проходит сквозь другую и ведет себя в дальнейшем так, как будто другой волны совсем не существовало.
Точно так же любое число звуковых волн может одновременно распространяться в воздухе, ничуть не мешая друг другу. Множество музыкальных инструментов в оркестре или голосов в хоре создает звуковые волны, одновременно улавливаемые нашим ухом.
Причем ухо может отличить один звук от другого.

Теперь посмотрим более внимательно, что происходит в местах, где волны накладываются одна на другую.
Наблюдая волны на поверхности воды от двух брошенных в воду камней, можно заметить, что некоторые участки поверхности не возмущены, в других же местах возмущение усилилось.
Если две волны встречаются в одном месте своими гребнями, то в этом месте возмущение поверхности воды усиливается.
Если же, напротив, гребень одной волны встречается с впадиной другой, то поверхность воды не будет возмущена.

Вообще же в каждой точке среды колебания, вызванные двумя волнами, просто складываются.
Результирующее смещение любой частицы среды представляет собой алгебраическую сумму смещений, которые происходили бы при распространении одной из волн в отсутствие другой.

Интерференция

Сложение в пространстве волн, при котором образуется постоянное во времени распределение амплитуд результирующих колебаний частиц среды, называется интерференцией.

Выясним, при каких условиях наблюдается интерференция волн.
Для этого рассмотрим более подробно сложение волн, образующихся на поверхности воды.

Можно одновременно возбудить две круговые волны в ванне с помощью двух шариков, укрепленных на стержне, которые совершают гармонические колебания.
В любой точке М на поверхности воды будут складываться колебания, вызванные двумя волнами (от источников O₁ и O₂).
Амплитуды колебаний, вызванных в точке М обеими волнами, будут, вообще говоря, различаться, так как волны проходят различные пути d₁ и d₂.
Но если расстояние l между источниками много меньше этих путей (l « d₁ и l « d₂), то обе амплитуды можно считать практически одинаковыми.

Условие максимумов

На рисунке изображена зависимость от времени смещений х₁ и х₂, вызванных двумя волнами при Δd = λ.

Разность фаз колебаний равна нулю (или, что то же самое, 2π, так как период синуса равен 2π).
В результате сложения этих колебаний возникают результирующие колебания с удвоенной амплитудой.
Колебания результирующего смещения х на рисунке показаны цветной штриховой линией.
То же самое будет происходить, если на отрезке Δd укладывается не одна, а любое целое число длин волн.

Амплитуда колебаний частиц среды в данной точке максимальна, если разность хода двух волн, возбуждающих колебания в этой точке, равна целому числу длин волн:

Δd = ±kλ

Условие минимумов

Пусть теперь на отрезке Ad укладывается половина длины волны.
Очевидно, что при этом вторая волна отстает от первой на половину периода.
Разность фаз оказывается равной л, т. е. колебания будут происходить в противофазе.

В результате сложения этих колебаний амплитуда результирующих колебаний равна нулю, т. е. в рассматриваемой точке колебаний нет.
То же самое произойдет, если на отрезке укладывается любое нечетное число полуволн.

Амплитуда колебаний частиц среды в данной точке минимальна, если разность хода двух волн, возбуждающих колебания в этой точке, равна нечетному числу полуволн:

На рисунке показана фотография интерференционной картины для двух круговых волн от двух источников (черные кружки).
Белые участки в средней части фотографии соответствуют максимумам колебаний, а темные — минимумам.

Когерентные волны

Для образования устойчивой интерференционной картины необходимо, чтобы источники волн имели одинаковую частоту и разность фаз их колебаний была постоянной.

Источники, соответствующие этим двум условиям, называются когерентными.
Когерентными называют и созданные ими волны.
Только при сложении когерентных волн образуется устойчивая интерференционная картина.

Если же разность фаз колебаний источников не остается постоянной, то в любой точке среды разность фаз колебаний, возбуждаемых двумя волнами, будет меняться с течением времени.
Поэтому амплитуда результирующих колебаний с течением времени будет непрерывно изменяться.
В результате максимумы и минимумы перемещаются в пространстве, и интерференционная картина размывается.

Распределение энергии при интерференции

Волны несут энергию.
Что же с этой энергией происходит при гашении волн друг другом?
Может быть, она превращается в другие формы, и в минимумах интерференционной картины выделяется тепло?
Ничего подобного!

Наличие минимума в данной точке интерференционной картины означает, что энергия сюда не поступает совсем.
Вследствие интерференции происходит перераспределение энергии в пространстве.
Она не распределяется равномерно по всем частицам среды, а концентрируется в максимумах за счет того, что в минимумы не поступает вовсе.

Обнаружение интерференционной картины доказывает, что мы наблюдаем волновой процесс.
Волны могут гасить друг друга, а сталкивающиеся частицы никогда не уничтожают друг друга целиком.
Интерферируют только когерентные (согласованные) волны.

Источник

Интерференционные тайны природы

В течение нескольких сотен лет физики пытались понять, что же такое свет — волны или поток частиц, названных позднее фотонами, и в конце концов выяснили, что слово «или» употреблять нельзя. В одних случаях свет ведёт себя как волна, в других — как поток фотонов, проявляя квантовый, то есть дискретный характер излучения. Другими словами, свет имеет двойственную природу. На научном языке это называется «корпускулярно-волновой дуализм» (слово «корпускула» означает «частица»). Интерференция считается одним из нагляднейших проявлений волновых свойств: ведь интерферировать могут только волны. Казалось бы, и спорить не о чем. Однако всё не так просто. Недаром существует весьма выразительное изречение: «Свет — самое тёмное место в физике».

Интерференция — замечательное явление, имеющее множество применений. Оно проявляется как в оптическом, так и в радиодиапазоне. Особенно впечатляюща интерференция света, так как мы можем её наблюдать непосредственно, в то время как радиоволны невидимы глазом. Часто интерференцию света характеризуют такой «парадоксальной» фразой: свет плюс свет может давать темноту. Человеку, совершенно незнакомому с физической оптикой, это может показаться очень странным: как это так — если к свету прибавить ещё свет, то должно стать ещё светлее! Правда, все мы изучали физику в школе, и, наверное, всё-таки у каждого остались хотя бы какие-то смутные воспоминания о том, что такое интерференция («Да. что-то связанное со светом. не очень помню, но вроде бы это какое-то наложение световых волн. »). Уже хорошо! Давайте же начнём с того, что освежим эти полузабытые знания, которые позволят нам побеседовать о крайне удивительных и интересных явлениях, связанных с интерференцией света.

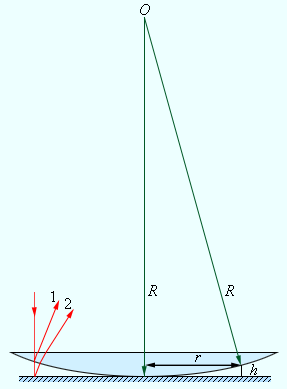
Возьмём более или менее «направленный» источник света, например карманный фонарик (с галогенной лампочкой, дающей яркий свет, а ещё лучше — со светодиодом), и направим его на белый экран. На экране возникнет пятно света. Теперь возьмём второй такой же фонарик и направим его свет на то же место экрана. «И что, мы получим темноту?» — иронически спросит читатель, прочитавший предыдущий абзац, но настолько позабывший школьную физику, что слово «оптика» ассоциируется у него лишь с очками и лупами. Нет, конечно, никакой темноты мы не получим, световое пятно станет ещё ярче. «Ну и что в этом удивительного?» — заметит наш скептик. В этом — ничего. Но теперь сделаем следующее: возьмём лист плотного картона, проколем в нём иголкой две дырочки как можно ближе одну к другой (скажем, на расстоянии 0,5 миллиметра), поставим лист перед экраном (на расстоянии около 20–30 см) и осветим эти дырочки одним фонариком (см. рис. 1). Возможно, придётся немного порегулировать расстояние между фонариком и картоном, но мы обязательно найдём положение, при котором на экране светлое пятно будет пересекаться тёмными участками. Вот мы и получили темноту!

Почему же возникают эти тёмные участки? Почему их не было в случае двух фонариков, а появились они только при освещении отверстий в картоне одним фонариком?

Зададим такой «нелепый» вопрос. Сколько источников света было в этих двух случаях? Я назвал этот вопрос «нелепым» потому, что он может вызвать недоумение: как сколько? В первом случае мы включали оба фонарика, значит, было два источника света, а во втором светил только один фонарик, один источник света. Разве не так?

Нет, не так. Во втором случае было тоже два источника, которыми стали два отверстия в картоне (1 и 2, рис. 1). То есть исходный источник был, конечно, один, но свет на экран шёл из этих двух дырочек, которые играли роль вторичных источников света. А вот то, что свет этих вторичных источников образовался от одного исходного, сыграло фундаментальную роль.

Используя картон с дырочками, изображённый на рис. 1, мы воспроизвели (с некоторыми несущественными отличиями) знаменитый опыт Т. Юнга, впервые наблюдавшего интерференцию света от двух щелей в 1802 году.

Интерференция — это такое сложение волн, при котором происходит не просто суммирование интенсивностей этих волн, а их взаимное усиление в одних точках пространства и ослабление в других, в зависимости от разности фаз волн в этих точках.

Но прежде чем рассматривать интерференцию, необходимо поговорить об одном фундаментальном понятии, играющем ключевую роль.

Почему в случае с двумя фонариками происходило только суммирование интенсивностей (яркостей), а в случае с картоном мы могли наблюдать интерференцию? Потому, что в первом случае световые волны от двух источников были некогерентны, а во втором — когерентны, так как порождены одним источником. Следовательно, необходимым условием образования интерференции является когерентность волн. Что это такое?

Слово «когерентность» — греческого происхождения и в наиболее общем смысле означает «согласованность». Простейший пример: когда по улице прогуливается толпа людей, она идёт некогерентно, а когда марширует рота солдат, то она идёт когерентно.

Когерентные волны — это волны одинаковой частоты, между которыми сохраняется постоянная разность фаз (то есть они согласованы по фазе). При сложении двух когерентных волн одинаковой поляризации (с одним и тем же направлением колебаний напряженности электрического поля) амплитуда суммарной волны зависит от разности фаз складываемых волн — это и есть интерференция.

При интерференции световых волн удобнее иметь дело не с амплитудами, а с интенсивностями. Это не меняет существа дела, так как интенсивность пропорциональна квадрату амплитуды. Если в какую-либо точку приходят две волны с интенсивностями I₁ и I₂ и фазами φ₁ и φ₂ соответственно, то результирующая интенсивность в этой точке определяется выражением

где ∆φ = |φ₁ – φ₂| — разность фаз, а множитель γ отражает степень когерентности волн. Из этой формулы наглядно видна зависимость результирующей интенсивности от разности фаз ∆φ и от величины γ.

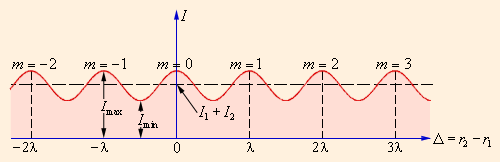
В тех местах, куда волны приходят в одинаковой фазе, то есть «гребни» и «впадины» одной волны совпадают с «гребнями» и «впадинами» другой (∆φ = 0, cos∆φ = 1), волны усиливают одна другую и наблюдается максимальная интенсивность (I_max). В тех местах, куда волны приходят в противофазе, «гребни» одной волны совпадают со «впадинами» другой (∆φ = 180°, cos∆φ = –1), волны гасят одна другую и результирующая интенсивность становится минимальной (I_min ). Таким образом, образуется интерференционная картина, состоящая из чередующихся светлых и тёмных участков.

Когерентность волн определяет их способность к интерференции. Практическим критерием степени постоянства разности фаз, то есть мерой степени когерентности γ, является контраст (видность, резкость, чёткость) интерференционных полос — важнейший параметр интерференционной картины. Если условие ∆φ = const не соблюдается, то, как видно из вышеприведённой формулы, изменяется и результирующая интенсивность I_рез, что приводит к «размытию» интерференционных полос — уменьшению контраста К. В общем случае контраст определяется выражением

Источник