какие волны можно считать когерентными
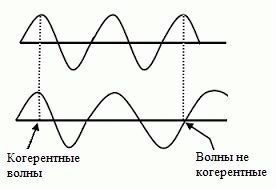
Когерентные волны
Когерентные волны
Для образования устойчивой интерференционной картины необходимо, чтобы источники волн имели одинаковую частоту и разность фаз их колебания была постоянной. Источники, удовлетворяющие этому условию, называются когерентными*.
Волны таких источников также называются когерентными.
Когерентность волн бывает временной и пространственной. Источники, у которых разность фаз остается постоянной, называются когерентными. Наиболее простой способ создать когерентные источники – это использовать реальный источник и его изображение. Существуют различные способы создания когерентных источников. Основные схемы наблюдения интерференции в немохроматическом свете используют деление волнового фронта (обычно от точечного источника) или деление амплитуды волны. При этом создаются две когерентных волны, которые интерферируют при небольшой разности хода.
Согласованность волн, которая заключается в том, что разность фаз остается неизменной с течением времени для любой точки пространства называется временной когерентностью.
Согласованность волн, которая заключается в том, что разность фаз остается постоянной в разных точках волновой поверхности, называется пространственной когерентностью.
Реальные источники практически не могут быть когерентными.
См. также
Смотреть что такое “Когерентные волны” в других словарях:
когерентные волны — Волны, разность фаз которых не зависит от времени. [Система неразрушающего контроля. Виды (методы) и технология неразрушающего контроля. Термины и определения (справочное пособие). Москва 2003 г.] Тематики виды (методы) и технология неразр.… … Справочник технического переводчика
когерентные волны — koherentinės bangos statusas T sritis fizika atitikmenys: angl. coherent waves vok. kohärente Wellen, f rus. когерентные волны, f pranc. ondes cohérentes, f … Fizikos terminų žodynas
когерентные волны — (связанные волны) волны одинаковой частоты, колебания в которых отличаются постоянной разностью фаз, не изменяющейся со временем … Русский индекс к Англо-русскому словарь по музыкальной терминологии
когерентные световые волны — Световые волны, имеющие постоянную разность фаз световых колебаний в течение данного отрезка времени. [Сборник рекомендуемых терминов. Выпуск 79. Физическая оптика. Академия наук СССР. Комитет научно технической терминологии. 1970 г.] Тематики… … Справочник технического переводчика
ВОЛНЫ — (1) (см.), распространяющиеся с конечной скоростью в пространстве и несущие с собой энергию без переноса вещества; (2) В. де Бройля проявляются при движении любой микрочастицей и отражают одновременное сочетание волновых и корпускулярных свойств… … Большая политехническая энциклопедия
электромагнитные волны — электромагнитное поле, распространяющееся в пространстве с конечной скоростью, зависящей от свойств среды. В вакууме скорость распространения электромагнитной волны с≈300 000 км/с (см. Скорость света). В однородных изотропных средах направления… … Энциклопедический словарь
Когерентность — (от латинского cohaerens находящийся в связи) согласованное протекание во времени нескольких колебательных или волновых процессов, проявляющееся при их сложении. Колебания называются когерентными, если разность их фаз остаётся постоянной… … Большая советская энциклопедия
Интерференция (физич.) — Картина интерференции двух круговых когерентных волн, в зависимости от длины волны и расстояния между источниками Интерференция волн наложение волн, при котором происходит их взаимное усиление в одних точках пространства и ослабление – в других.… … Википедия
Интерференция волн — Это статья об интерференции в физике. См. также Интерференция и Интерференция света Картина интерференции большого количества круговых когерентных волн, в зависимости от длины волны и расстояния между источниками Интерференция волн взаимное … Википедия
Интерференция (физика) — Это статья об интерференции в физике. См. также Интерференция (неоднозначность) и Интерференция света Картина интерференции двух круговых когерентных волн, в зависимости от длины волны и расстояния между источниками Интерференция волн нелинейное… … Википедия
Когерентность волн
В этой статье мы расскажем, что означает понятие когерентности, определим ее основные виды (временная и пространственная), а также решим несколько задач, связанных с оценкой когерентности. Начнем с базового определения.
При наблюдении интерференции волн одним из важнейших условий является их когерентность. О наличии когерентности говорят тогда, когда имеет место согласованность протекания волновых или колебательных процессов во времени и пространстве.
Когерентность характеризуется такой чертой, как степень (иначе ее можно назвать степенью согласованности вышеуказанных процессов). Различают два основных типа данного явления – временную и пространственную когерентность.
Что такое временная когерентность
Данный тип когерентности характеризуется длиной и продолжительностью. Она возникает тогда, когда мы имеем дело с немонохромным точечным источником света. Примером могут быть полосы, наблюдаемые при интерференции в специальном приборе – интерферометре Майкельсона: чем выше оптическая разность, тем менее четкими становятся полосы (вплоть до полного исчезновения). Основная причина временной когерентности света лежит в длине источника и конечном времени свечения.
В таком случае исследуемые волны когерентными не являются. Если же за указанное время величина cos δ ( t ) сохраняется практически неизменной, то интерференция становится очевидной, и у нас получаются когерентные волны.
Из всего этого можно сделать вывод об относительности понятия когерентности. При малой инерционности прибора интерференция, как правило, обнаруживается, а если прибор обладает большим временем инерции, то нужную картину мы можем просто не увидеть.
Время когерентности имеет зависимость от интервала частот, а также от длины волн, представленных в общей световой волне.
Что такое пространственная когерентность
Если мы имеем дело с монохроматическим протяженным, а не точечным источником света, то здесь вводится понятие пространственной когерентности. Она имеет такие характеристики, как ширина, радиус и угол.
Буквой φ обозначен угловой размер источника световой волны.
Если волна света располагается вблизи нагретого тела, то ее пространственная когерентность составляет всего несколько длин волн. Чем больше расстояние от источника света, тем выше степень пространственной когерентности.
Чтобы оценить радиус когерентности, воспользуемся формулой ρ k o g
Интерференция солнечных лучей не может быть видна невооруженным взглядом, поскольку радиус ее когерентности очень мал и находится вне разрешающей способности человеческого глаза.
Условие: если два не связанных между собой источника света испускают волны, почему данные волны не будут когерентными?
Когерентные волны
Когерентные волны – это колебания с постоянной разностью фаз. Разумеется, условие выполняется не в каждой точке пространства, лишь на отдельных участках. Очевидно, что для удовлетворения определению частоты колебаний также предвидятся равными. Прочие волны бывают когерентны лишь на некотором участке пространства, а дальше разность фаз меняется, и это определение использовать уже нельзя.
Обоснование применения
Когерентные волны считаются упрощением, не встречающимся на практике. Математическая абстракция помогает во многих отраслях науки: космос, термоядерные и астрофизические исследования, акустика, музыка, электроника и, конечно, оптика.
Для реальных приложений применяются упрощённые методы, в числе последних трёхволновая система, основы применимости кратко изложены ниже. Для анализа взаимодействия возможно задать, к примеру, гидродинамическую или кинетическую модель.
Решение уравнений для когерентных волн позволяет предсказать устойчивость систем, функционирующих с использованием плазмы. Теоретический подсчёт показывает, что иногда амплитуда результата за короткое время растёт бесконечно. Что означает создание взрывоопасной ситуации. Решая уравнения для когерентных волн, подбором условий удаётся избежать неприятных последствий.
Определения
Вначале введём ряд определений:
Понятие когерентности
Советская энциклопедия говорит, что волны одинаковой частоты неизменно когерентны. Это верно исключительно для отдельно взятых неподвижных точек пространства. Фаза определяет результат сложения колебаний. К примеру, противофазные волны одной амплитуды дают прямую линию. Такие колебания гасят друг друга. Самая большая амплитуда у синфазных волн (разность фаз равна нулю). На этом факте основан принцип действия лазеров, зеркальная и фокусирующая система пучков света, особенности получения излучения делают возможной передачу информации на колоссальные расстояния.
Согласно теории взаимодействия колебаний когерентные волны образуют интерференционную картину. У новичка возникает вопрос: свет лампочки не кажется полосатым. По простой причине, что излучение не одной частоты, а лежит в пределах отрезка спектра. И участок, причём, приличной ширины. Из-за неоднородности частот волны беспорядочные, не проявляют свои теоретически и экспериментально в лабораториях обоснованные и доказанные свойства.
Хорошей когерентностью обладает луч лазера. Его используют для связи на дальние расстояния при прямой видимости и прочих целей. Когерентные волны дальше распространяются в пространстве и на приёмнике подкрепляют друг друга. В пучке света разрозненной частоты эффекты способны вычитаться. Возможно подобрать условия, что излучение исходит от источника, но на приёмнике не зарегистрируется.
Обычный свет лампочки тоже работает не на полную мощность. Достичь КПД в 100% на современном этапе развития техники не представляется возможным. К примеру, газоразрядные лампы страдают сильной дисперсией частот. Что касается светодиодов, основатели концепции нанотехнологий обещали создать элементную базу для производства полупроводниковых лазеров, но напрасно. Значительная часть разработок засекречена и рядовому обывателю недоступна.
Лишь когерентные волны проявляют волновые качества. Действуют согласованно, как лучинки веника: по одной легко сломать, вместе взятые – выметают мусор. Волновые свойства – дифракция, интерференция и рефракция – характерны для всех колебаний. Просто зарегистрировать эффект сложнее из-за беспорядочности процесса.
Когерентные волны не демонстрируют дисперсии. Показывают одну частоту и одинаково отклоняются призмой. Все примеры волновых процессов в физике даются, как правило, для когерентных колебаний. На практике приходится учитывать присутствующую малую ширину спектра. Что накладывает особенности на процесс расчёта. Как зависит реальный результат от относительной когерентности волны – пытаются ответить многочисленные учебники и разрозненные издания с замысловатыми названиями! Единого ответа не существует, он сильно зависит от отдельно взятой ситуации.
Волновые пакеты
Для облегчения решения практической задачи можно ввести, к примеру, определение волнового пакета. Каждый из них разбивается дальше на мелкие части. И эти подразделы взаимодействуют когерентно между аналогичными частотами другого пакета. Подобный аналитический метод широко распространён в радиотехнике и электронике. В частности, понятие спектра изначально вводилось для того, чтобы дать в руки инженеров надёжный инструмент, позволяющий оценить поведение сложного сигнала в конкретных случаях. Оценивается малая толика воздействия каждого гармонического колебания на систему, потом конечный эффект находится их полным сложением.
Следовательно, при оценке реальных процессов, не являющихся даже близко когерентными, допустимо разбить объект анализа на простейшие составляющие, чтобы оценить результат процесса. Расчёт упрощается с применением вычислительной техники. Машинные эксперименты показывают достоверность формул для имеющейся ситуации.
На начальном этапе анализа полагают, что пакеты с малой шириной спектра возможно условно заменить гармоническими колебаниями и в дальнейшем пользоваться обратным и прямым преобразованием Фурье для оценки результата. Эксперименты показали, что разброс фаз между выбранными пакетами постепенно возрастает (колеблется с постепенным увеличением разброса). Но для трёх волн разница постепенно сглаживается, согласуясь с излагаемой теорией. Накладывается ряд ограничений:
Доказано, что в такой среде каждой волне удаётся подобрать конечный спектр, что автоматически делает возможным машинный анализ, а при взаимодействии пакетов спектр результирующей волны уширяется. Колебания по сути когерентными не считаются, но описываются уравнением суперпозиции, представленном ниже. Где волновой вектор ω(k) определяется по дисперсионному уравнению; Еk признано амплитудой гармоники рассматриваемого пакета; k – волновое число; r – пространственная координата, для показателя решается представленное уравнение; t – время.
Время когерентности
В реальной ситуации разнородные пакеты когерентны лишь на отдельном интервале. А далее расхождение фаз становится слишком большим, чтобы применять описанное выше уравнение. Чтобы вывести условия возможности вычислений, вводится понятие времени когерентности.
Полагается, что в начальный момент фазы всех пакетов одинаковы. Выбранные элементарные доли волны когерентны. Тогда искомое время находится как отношение числа Пи к ширине спектра пакета. Если время превысило когерентное, в данном участке уже нельзя использовать формулу суперпозиции для сложения колебаний – фазы слишком сильно отличаются друг от друга. Волна уже не когерентна.
Пакет возможно рассматривать, словно он характеризуется случайной фазой. В этом случае взаимодействие волн идёт по отличающейся схеме. Тогда находятся фурье-компоненты по указанной формуле для дальнейших расчётов. Причём взятые для расчёта две прочие компоненты берутся из трёх пакетов. Это случай совпадения с теорией, упомянутый выше. Следовательно, уравнение показывает зависимость всех пакетов. Точнее – результата сложения.
Для получения наилучшего результата нужно, чтобы ширина спектра пакета не превышала числа Пи, делённого на время решения задачи суперпозиции когерентных волн. При расстройке частоты амплитуды гармоник начинают осциллировать, точный результат получить сложно. И наоборот, для двух когерентных колебаний формула сложения упрощается максимально. Амплитуда находится как квадратный корень из суммы исходных гармоник, возведённых в квадрат и сложенных с собственным удвоенным произведением, помноженным на косинус разности фаз. У когерентных величин угол равен нулю, результат, как уже указано выше, получается максимальным.
Наравне с временем и длиной когерентности используют термин «длина цуга», что является аналогом второго термина. Для солнечного света эта дистанция составляет один микрон. Спектр нашего светила крайне широкий, что объясняет настолько мизерную дистанцию, где излучение считается когерентным самому себе. Для сравнения, длина цуга газового разряда достигает 10 см (в 100000 раз больше), а у лазера излучение сохраняет свойства и на километровых расстояниях.
С радиоволнами намного проще. Кварцевые резонаторы позволяют достичь высокой когерентности волны, чем объясняются пятна уверенного приёма на местности, граничащие с зонами молчания. Аналогичное проявляется при изменении имеющейся картины с течением суток, движением облаков и прочими факторами. Изменяются условия распространения когерентной волны, и интерференционная суперпозиция оказывает влияние в полной мере. В радиодиапазоне на низких частотах длина когерентности может превышать поперечник Солнечной системы.
Условия сложения сильно зависят от формы фронта. Наиболее просто задача решается для плоской волны. В действительности фронт обычно является сферическим. Точки синфазности находятся на поверхности шара. В бесконечно удалённой от источника местности условие плоскости возможно принять за аксиому, и дальнейший расчёт вести согласно взятому постулату. Чем ниже частота, тем проще создать условия для выполнения расчёта. И наоборот, источники света со сферическим фронтом (вспомним Солнце) сложно подогнать под стройную теорию, написанную в учебниках.
Какие волны называются когерентными?
Для образования устойчивой интерференционной картины необходимо, чтобы источники волн имели одинаковую частоту и разность фаз их колебания была постоянной. Источники, удовлетворяющие этому условию, называются когерентными*.
Волны таких источников также называются когерентными.
Когерентность волн бывает временной и пространственной. Источники, у которых разность фаз остается постоянной, называются когерентными. Наиболее простой способ создать когерентные источники – это использовать реальный источник и его изображение. Существуют различные способы создания когерентных источников. Основные схемы наблюдения интерференции в немохроматическом свете используют деление волнового фронта (обычно от точечного источника) или деление амплитуды волны. При этом создаются две когерентных волны, которые интерферируют при небольшой разности хода.
Волны таких источников также называются когерентными.
Когерентность волн бывает временной и пространственной. Источники, у которых разность фаз остается постоянной, называются когерентными. Наиболее простой способ создать когерентные источники – это использовать реальный источник и его изображение. Существуют различные способы создания когерентных источников. Основные схемы наблюдения интерференции в немохроматическом свете используют деление волнового фронта (обычно от точечного источника) или деление амплитуды волны. При этом создаются две когерентных волны, которые интерферируют при небольшой разности хода.
Согласованность волн, которая заключается в том, что разность фаз остается неизменной с течением времени для любой точки пространства называется временной когерентностью.
Какие волны называются когерентными? Как их получить? Какова ширина интерференционных полос в опыте Юнга? Как влияют размеры источника на интерференционную картину?
Когерентные волны – волны, имеющие одинаковые частоты, постоянную разность фаз, а колебания происходят в одной плоскости.
.
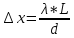
Протяженный источник состоит из большого числа точечных взаимно некогерентных элементов. Поэтому интенсивность в любом месте равна сумме интенсивностей в интерференционных картинах, создаваемых отдельными точечными элементами источника.
В интерференционных опытах по методу деления волнового фронта полосы на экране перпендикулярны плоскости, в которой находятся первичный точечный источник S и вторичные источники S1 и S2. Использование вместо S линейного источника, т.е. достаточно узкой щели, вытянутой перпендикулярно этой плоскости, увеличивает интенсивность и не приводит к ухудшению четкости интерференционных полос. Однако увеличение ширины щели приводит к тому, что полосы становятся менее четкими или пропадают совсем.
Если размеры источника (т.е. ширина щели S) много меньше длины световой волны, то интерференционная картина будет резкой, так как разность хода интерферирующих лучей от любой точки источника до некоторой точки наблюдения P будет практически одна и та же. Но обычно размеры источника значительно больше длины волны, поэтому одинаковые интерференционные картины от разных его элементов сдвинуты одна относительно другой. В результате наложения этих картин интерференционные полосы оказываются более или менее размытыми. Их можно наблюдать лишь при выполнении определенных условий, налагаемых на геометрию эксперимента. Эти условия подробно обсуждаются ниже.
Опишите явление интерференции в тонкой плёнке. Как изменяется наблюдаемая картина при изменении толщины плёнки?
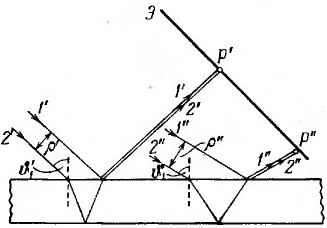
Плоскопараллельная пластинка. Обе плоские отраженные волны распространяются в одном направлении, образующем с нормалью к пластинке угол, равный углу падения θ1. Эти волны смогут интерферировать, если будут соблюдены условия как временной, так и пространственной когерентности.
Для того чтобы имела место временная когерентность, разность хода не должна превышать длину когерентности; равную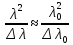 
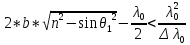
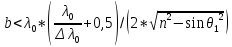
. Следовательно, должно соблюдаться условие
или
.
В полученном соотношении половиной можно пренебречь по сравнению с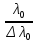 
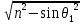
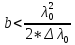
. Выражение 
имеет величину порядка единицы. Поэтому можно написать
.
(удвоенная толщина пластинки должна быть меньше длины когерентности).
Положив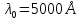 
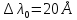
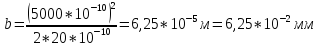
и 
, получим предельное значение толщины, равное
Теперь рассмотрим условия соблюдения пространственной когерентности. Поставим на пути отраженных пучков, экран. Приходящие в точку Р’ лучи 1′ и 2′ отстоят в падающем пучке на расстояние ρ’. Если это расстояние не превышает радиуса когерентности ρког падающей волны, лучи 1′ и 2′ будут когерентными и создадут в точке P’ освещенность, определяемую значением разности хода Δ, отвечающим углу падения θ1‘. Другие пары лучей, идущие под тем же углом θ1‘, создадут в остальных точках экрана такую же освещенность. Таким образом, экран окажется равномерно освещенным. При изменении наклона пучка освещенность экрана будет меняться.
Видно, что расстояние между падающими лучами 1 и 2 равно
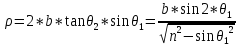
Если принять n=1,5, то для θ1=45° получается ρ=0,8*b, а для θ1= 10° – ρ=0,1*b. Для нормального падения ρ=0 при любом n.
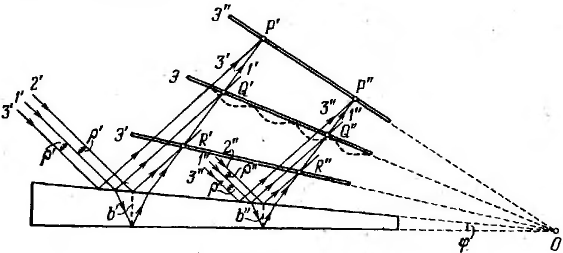
Пластинка переменной толщины. Возьмем пластинку в виде клина с углом при вершине φ. Пусть на нее падает параллельный пучок лучей. Теперь лучи, отразившиеся от разных поверхностей пластинки, не будут параллельными. Два до падении на пластинку практически сливающихся луча 1′ пересекаются после отражения в точке Q’. Два практически сливающихся луча 1″ пересекаются в точке Q”. Можно показать, что точки Q, Q’ и другие аналогичные им точки лежат в одной плоскости, проходящей через вершину клина О. Отразившийся от нижней поверхности клина луч 1′ и отразившийся от верхней поверхности луч 2′ пересекутся в точке R’, расположенной ближе к клину, чем Q’. Аналогичные лучи 1′ и 3′ пересекутся в точке P’ отстоящей от поверхности клина дальше, чем О’.
Направления распространения волн, отраженных от верхней и нижней поверхностей клина, не совпадают. Временная когерентность будет соблюдаться только для частей волн, отразившихся от мест клина, для которых толщина удовлетворяет условию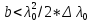 
. Допустим, что это условие выполняется для всего клина. Кроме того, предположим, что радиус когерентности намного превышает длину клина. Тогда отраженные волны будут когерентными во всем пространстве над клином, и при любом расстоянии экрана от клина на нем будет наблюдаться интерференционная картина в виде полос, параллельных вершине клина О. Так, в частности, обстоит дело при освещении клина светом испускаемым лазером.
При смещении экрана из положения Э в направлении от клина или к клину начинает сказываться степень пространственной когерентности падающей волны. Если в положении экрана, Э’ расстояние ρ’ между падающими лучами 1′ и 2′ станет порядка радиуса когерентности, интерференционная картина на экране Э’ наблюдаться не будет. Аналогично картина исчезает в положении экрана, обозначенном через Э”.